试卷分析中学生成绩的正态检验*

◆陈秋凤 周防震 袁德培

1 前言

试卷分析是教师完成教学工作的重要环节之一，学生成绩分布是试卷分析的重要组成部分。成绩正态分布是一种概率分布的特殊表现形式，在统计某次考试成绩分布规律的时候，将成绩按分数段制成统计图，如果成绩分布图中中等成绩占最多数，其余成绩以中等成绩为中轴，向两侧逐次降低，则称这次成绩呈正态分布。然而在实践中，教师在进行学生成绩分布的正态性分析时常常存在主观臆断，只要看到有“两头低、中间高”的趋势，就主观认为符合正态分布，否则就认为不符合正态分布。

2 学生成绩的正态检验

图1为生物制药工程与设备课程学生成绩的频次图，可以看出成绩分布与正态分布有些许偏差。教师在试卷分析时容易存在主观偏见，即不加检验，认为学生成绩不符合正态分布。事实上，某次考试学生成绩分布是否真正服从正态分布，需要进行正态性检验。

正态概率图 概率图（probability-probability plot，P-P plot）是以实际或观察的累积频率（X）对被检验分布的理论或期望累积频率作图（Y）。如果所分析的数据来自正态分布，正态P-P图图形的散点应该呈现一条直线。图2为生物制药工程与设备课程考试74个学生成绩的P-P图，可以看出散点近似在一条直线，中部散点较多地靠近直线上方。

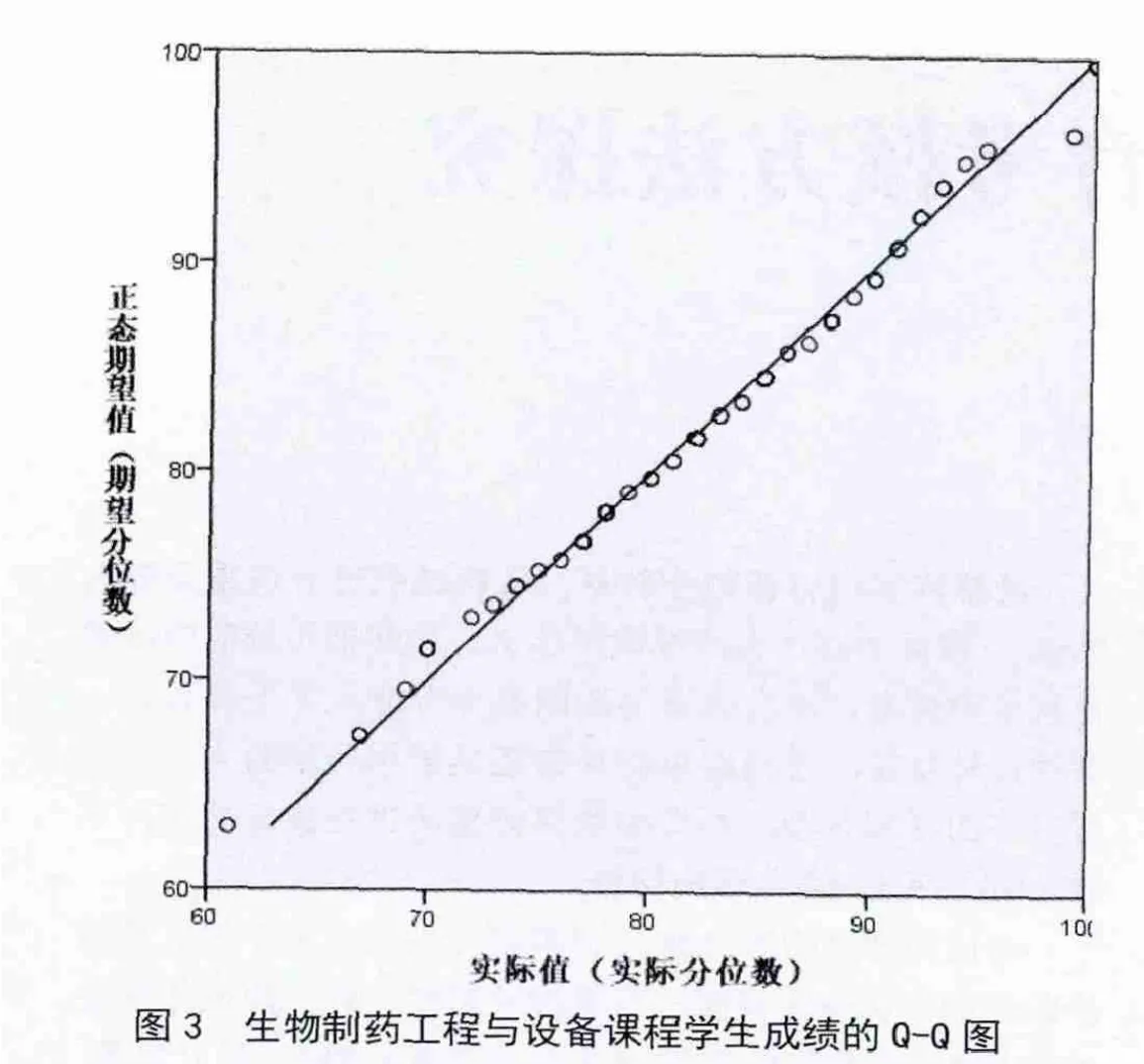
分位数图 分位数图（quantile-quantile piot，Q-Q plot）是以实际或观察的分位数（X）对被检验分布的理论或期望分位数（Y）作图。如果所分析的数据来自正态分布，则Q-Q图上的数据点应分布在从左下到右上的直线附件，否则数据点偏离直线较远。图3为生物制药工程与设备课程考试74个学生成绩的Q-Q图，可以看出散点近似在一条直线，且拟合程度比P-P图（图2）好，说明利用图示法进行正态性检验，Q-Q图的效率比P-P图高。

矩法 矩法（method of moment，又称动差法）是利用数学上的矩原理来检验偏度和峰度。偏度指分布不对称的程度和方向，用偏度系数（coefficient of skewness）来衡量，样本偏度系数用g1表示，总体偏度系数用γ1表示；而峰度则指分布与正态曲线相比的冒尖程度或扁平程度，用峰度系数（coefficient of kurtosis）衡量，样本峰度系数用g2表示，总体峰度用γ2表示。理论上，总体偏度系数γ1=0为对称，γ1＞0为正偏态，γ1＜0为负偏态；总体峰度系数γ2=0为正态峰，γ2＞0为尖峭峰，γ2＜0为平阔峰。只有同时满足对称和正态峰两个条件时，才能认为资料服从正态分布[1]。其中g1和g2统计量的计算公式为：

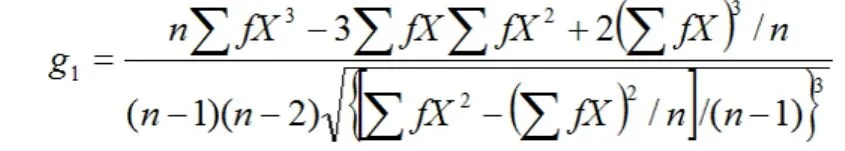
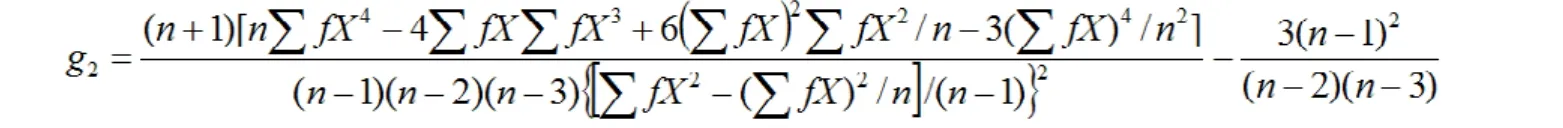
式中X为变量值，f为相同X值的个数，n为样本含量。当用原始数据进行计算时，f=1。因此，上两式无论n的大小均适用。g1和g2统计量的标准误计算公式为：

g1和g2的抽样分布近似正态分布，故可用μ检验进行正态性检验。

1）建立假设检验，确定检验标准。

H0：γ1=0且γ2=0，即总体服从正态分布。

H1：γ1≠0或（和）γ2≠0，即总体不服从正态分布。

α=0.10（欲不拒绝H0，α宜稍大以减少Ⅱ型错误）。

2）计算检验统计量。利用生物制药工程与设备课程考试74个学生成绩的原始数据，f=1，X为74个学生成绩。

令 ∑fX=∑X=6239，∑fX2=∑X2=531 843，∑fX3=∑X3=45 811 973，∑fX4=∑X4=3 985 200 975，按上述公式计算得g1和g2分别为-0.214 0和-0.279 5；σg1和σg2分别为0.279 2和0.551 7。故有：

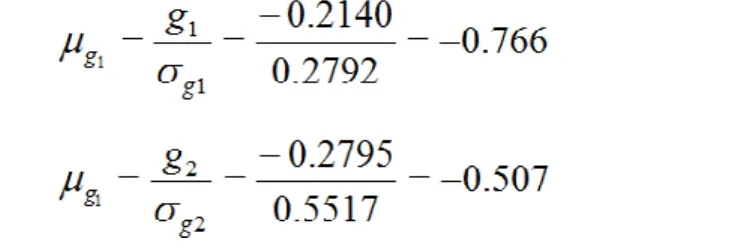
3）确定P值，做出推断结论。查μ界值表，双尾检测，μ0.05=1.64，可见峰度P＞0.05，偏度P＞0.05。按照α=0.10水平，不能拒绝H0，无统计学意义，即尚不能认为学生成绩的总体不服从正态分布。

3 结语

从学生成绩频次图（图1）直观判断，容易认为生物制药工程与设备课程学生成绩的分布不符合正态分布；但图示法（包括P-P法和Q-Q法）和矩法结果均显示还不能认为该课程学生成绩的分布不服从正态分布，表明教师在进行学生成绩的正态性评价时，仅从成绩分布频次图进行直观判断容易陷入“主观”臆断，科学的判断需要借助于一定的正态检验方法。P-P和Q-Q图示法具有简单明了的特征，从本文可以看出，Q-Q图示法（分位数图法）拟合程度优于P-P图示法，说明其检验效率更高更好。但图示法只能定性，难以定量判断，而矩法具有明显的定量特征。尽管矩法涉及繁琐的公式计算，但借助于常用统计分析软件（如SPSS），很容易计算偏度（Skewness）系数g1和峰度（Kurtosis）系数g2两个统计量[2]，以及它们各自对应的标准误σg1和σg2。综合认为，借助SPSS等统计分析软件，矩法分析结合假设检验，是教师进行试卷分析时评价学生成绩符合正态分布与否的客观方法。■

[1]孙振球.医学统计学[M].北京:人民卫生出版社,2010.

[2]时立文.SPSS19.0统计分析从入门到精通[M].北京:清华大学出版社,2012.