目标评价：从“概念表象”走向“核心知识”——例谈教学目标评价的把握

于正军

（扬州市江都区实验小学，江苏扬州225200）

一、目标评价：从关注怎么看到关注看什么

教师、学生乃至教材，只要学生学到分数，就必然与“阴影部分”的字眼紧密连接起来，教师就会自然地带领学生走进“阴影部分”的世界。“阴影部分”就很自然地成为分数的“代名词”，抑或成为分数的“标签”，促使教师在课堂上引导学生把认识分数的思维集中点指向“阴影部分”，从而使学生形成对分数认识的“概念表象”：阴影部分就是分数。这抑制了学生对分数概念内涵的真实建构和分数意义的真正理解。

例如，在学生认识“几分之一”后，教师引领学生认识“几分之几”。课堂上教师出示：引导学生观察并思考：阴影部分表示多少生：。紧接出示：引导学生继续观察并追问：现在阴影部分表示多少？生（异口同声）：。教师（着急）：再看一看是多少？生（中下等生还是坚持）：。究其原因：教师教学时，一味地指引学生观察阴影部分，“阴影部分”已在学生的头脑中形成“思维表象”，这样一来，每当出示“阴影部分”时，学生就会把观察的思维集中点聚焦到“阴影部分”的变化上。第一幅图阴影部分涂了1份，第二幅图阴影部分涂了2份，学生理所当然地说出，这一思维现象符合儿童的认知特点和心理特征。因此教师教学在引导学生观察时，不要一味地强化对“阴影部分”的认知，以免误导学生机械地认为“阴影部分”就是分数，重要的是引导学生观察与“阴影部分”有关联的“其他区域”，促使学生对“阴影部分”与“其他部分”及整幅图之间位置、数量等关系的把握与理解，继而在建构分数概念内涵的过程中实现对分数“核心知识”的掌握与内化。

二、目标评价：从关注怎么算到关注算什么

随着口算在实际运用中不断“受阻”，笔算就随之产生了，即人们不能口算出得数时，需要借助笔算。这就给一线教师造成概念上的片面理解，认为笔算就是列竖式计算，二者在概念内涵上是等同的，课堂上只要教会学生会列竖式计算，学生就掌握了笔算，这就促使学生形成笔算的“概念表象”：笔算就是会竖式计算。殊不知会列竖式计算，只能证明学生已掌握了笔算的基本算法，即怎么用竖式进行计算，然而学生对于笔算过程中的数位、位数及数的大小含义等“算什么”的“核心知识”并未得到体验与理解。

例如，教学“两位数除以一位数笔算除法”，课堂上教师只是一味地带领学生掌握列竖式的书写格式及其试商方法，在经过几轮的训练后，由于此类笔算试商简单，所以全班学生都能很快掌握两位数除以一位数的竖式计算。因此，在课堂上学生做得既对又快，教师即认为本节课教学目标高效达成。其实如此教学，教师只是解决了“怎么算”的问题，至于笔算除法“算什么”的“核心知识”，学生根本无法涉足。在一次学生质量监测中，笔者出了这样一道题：□3÷6的商是两位数，□里面最小填（）；如果74÷□的商是一位数，□里最小填（）。在后续的学业质量监测结果分析时发现，学生在两个括号全部填正确的人数只占30%左右，这足以说明大部分学生在学会了除法竖式计算后对于笔算除法究竟是“算什么”的算理根本不会想，也不知道想什么。所以，笔算教学一定要在引领学生掌握“怎么算”的基础上，让学生思考被除数和除数之间的位数的关系、数位的关系及数的大小含义等“算什么”的“核心知识”，使学生不仅学会“怎么算”，还悟出为什么这样算的道理，在掌握笔算方法的同时，促进计算技能和计算数感的形成。

三、目标评价：从关注怎么解到关注解什么

在解方程的教学中，如果教师不能带领学生理解数学概念的核心内涵，学生只能在教师的带领下机械行走，被动模仿，不能真正理解解方程的真正数学含义，即只知道解，却不知道为何而解。在学生不能深入理解解方程的“行与思”的过程中，学生的头脑中就会逐渐形成解方程的数学“概念表象”，尤其是中下等生，即解方程就是求未知量的值。因此教师教学时，要能抓住数学概念“背后”的核心知识，引导学生展开数学思考，促使学生不仅知道怎么解，更重要的是对于方程解什么的“核心知识”的真正掌握。

例如，在教学“ax+bx=c”类型的方程中，学生竟然写出了如下解方程的过程：

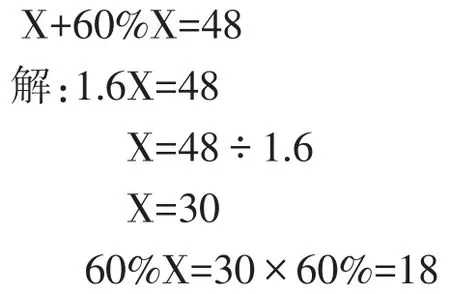
即，学生不仅求出x的值，还求出60%x的值，认为解方程就是把方程中所有未知项的值都求出来。而且在教师强调多次以后的训练中，如此的情况依然屡见不鲜。一方面说明学生对“解方程”的概念建立不深刻，认为“解方程”就是求未知项的值，不理解每道方程等式中每个未知项之间的关系。另一方面说明一线教师在引导学生解方程时，一味地强调教会学生解方程的方法及手段，注重凸显了“解方程”过程中“运算”的功能，却忽视了“解方程”背后未知项的含义，即“解方程”中“运算”的最终目标和结果指向谁？求方程“解”的过程是“解什么”的过程？学生只知道机械求出方程中所有未知项的值，而却很少对“方程”“解方程”“方程的解”等与方程有关的数学概念的“核心知识”进行深入的思考与反思。因此，在平时的教学实践中，一线教师要从学生思路出发，从数学概念内涵出发，引领学生领悟“解什么”比“怎么解”更具意义和价值，要使学生在掌握数学概念和形成数学技能的道路上做到先“思”而后“行”，唯有如此，才能有效促进学生数学思想与方法的感悟和形成。

四、目标评价：从关注怎么比到关注比什么

在数学知识的发展过程中，其概念形成过程中一直彰显着“生活意义”和“算术意义”两种特性，使数学知识既来源于生活又应用于生活。因此，提高学生的实践运用能力和解决实际问题能力，理应是贯穿于每节数学课的“守恒”目标。所以教学时，一方面教师要创设情境，让学生理解数学概念的“生活定义”，更重要的是要让学生把握“概念表象”背后的数学意义，从而促进学生灵活运用数学概念解决生活问题。

例如，一位教师在教学“比例尺”时，为了让学生能牢牢地记住比例尺是“图上距离∶实际距离”，而不能混淆为“实际距离∶图上距离”。课堂上教师引出丰富多彩的地图引导学生观察思考，何为图上距离？何为实际距离？最终揭示：比例尺就是“图上距离”与“实际距离”的比。课堂上看似学生学得兴致盎然，轻松接收。殊不知虽然“图上距离∶实际距离=比例尺”这个数学“概念表象”上呈现出“图上距离、实际距离”两个概念要素，可是在实际运用中，“图上距离”会如何呈现？“实际距离”又是如何呈现的？“比例尺”这个比所呈现的形式又是什么？这些隐藏在比例尺概念中的“核心知识”学生全然不知，所以真正让学生根据实际情境求比例尺时，学生的错误率极高，几乎没有学生能很快算出准确的比例尺。

究其原因，是教师在课堂上过多地引导学生关注“比例尺=图上距离∶实际距离”的“概念表象”，却忽略了比例尺概念“背后”的“核心知识”。如何使学生又对又快地得出“1∶（）”形式的比例尺，需要一线教师在教学时激活学生与比例尺相关联的已有知识和经验，引领学生真正走进比例尺概念含义的建构过程中。

例如，求比例尺：图上距离2.4厘米，实际距离60千米。虽然学生能很快得出比例尺就是2.4厘米∶60千米，可是怎样才能得出简洁、明了、规范的比例尺呢？课堂上大部分学生是一脸茫然，无从下手，不知道从哪儿开始着手思考。如果教师告诉学生这里首先进行长度单位的换算，再进行比的化简，学生依然错误率很高，因为在学生的头脑中对于求比例尺的一般方法和操作步骤是一片空白，这就需要教师在激活学生已有知识经验的基础上引导学生掌握求比例尺可操作的“抓手”。教学中可引导学生进行如下操作，学生一边规范书写一边思考：

2.4厘米：60千米=2.4：6000000=1：2500000

（1）“千米”化成“厘米”可以怎样想？引导学生逐步思考：1千米=1000米，1米=100厘米，所以，只需在“60”末尾先添几个0？再添几个0？

（2）把2.4∶6000000化简成1∶（）的形式可以怎样操作？生1：先把比的前项“2.4”转化成整数“24”，再把比的前后项同时除以24。生2：可以直接用60除以2.4再添上5个0。

学生经历如此求比例尺的过程后，就会在头脑中形成求比例尺的一般方法与步骤，继而形成解决问题的技能，这一过程就促使学生把长度单位的转化、比的性质、比的化简等与比例尺有关的“核心知识”迁移到比例尺的数学概念中去，使比例尺数学概念的内涵与外延在学生的脑海里得到建立与完善，促进学生对比例尺数学意义的深刻理解与建构。

综上所述，一线教师在进行课堂教学目标评价时，要从学生认知特点、思维特征及数学概念内涵出发，在穿透“概念表象”，挖掘“概念表象”背后“核心知识”的基础上，引导学生建立数学概念，促进学生深度把握数学知识的本质内涵，提高课堂教学的实效，促进学生数学思考力的提升。▲