基于数据驱动的锂电池随机动态系统建模

刘晓程 王建明 王 武

（福州大学电气工程与自动化学院，福州 350108）

随着经济的发展，以锂电池为能源载体的储能元件逐渐应用在人类生活的方方面面，从手机到笔记本电脑到混合动力汽车和电动汽车，锂电池受到越来越多的关注与研究[1]。为了对锂电池进行有效的能量管理，充分利用电能，延长锂电池寿命，提高系统的安全性和可靠性，就必须对锂电池进行建模、特性分析与参数估计。传统的基于模型驱动的锂电池模型有等效电路模型、电化学模型、神经网络模型和有限元模型等[2]，吸引了诸多专家学者进行研究。文献[3]中主要针对锂电池阻抗易受电荷状态、充放电、电解液均匀性等影响的问题，结合全电阻光谱学的应用建立了锂电池模型。文献[4]中主要针对锂电池等效电路模型的参数估计问题，对锂电池的有限带宽特性进行了介绍与分析并建立了相应的模型，提出了一种基于序列二次规划算法的模型参数估计方法。文献[5]中主要针对基于模型的锂电池参数在线实时估计问题中由于频率响应的限制而导致估计精度下降的问题，提出了基于两个时间尺度的参数估计方法，分别识别锂电池不同速度的动态反应过程，与传统单时间尺度的方法相比其频率响应更接近真实值。

但是，锂电池内部化学反应无法直接进行测量、反应过程复杂且易受外界环境影响，具有较强的非线性特性以及测量过程中存在噪声，因此上述基于模型驱动的机理建模方法存在一定偏差，无法准确建模。针对这一问题，本文根据数据驱动（Data-Driven）的思想，提出了一种基于数据驱动的锂电池随机动态系统建模。相对于传统的基于模型的建模方式，数据驱动的方法仅需要研究系统的在线或者离线数据，通过相应的算法仅依靠实验数据便可以建立相应的系统模型。文献[6]中提出了将数据驱动方法如自回归求和移动平均模型和人工神经网络用于预测中，并取得了很好的效果。文献[7]中提出了将数据驱动模型和物理模型结合的方法，并指明不仅要对锂电池的使用寿命进行准确的预测，而且还要对预测中的不确定性进行定量的分析，其首次将高斯过程回归（Gaussian Processes Regression，GPR）模型用于锂电池的预测，但由于效果不佳和相对复杂，只是简单提到，没有继续深入探讨和研究。上述文献主要解决依靠数据驱动的方法进行锂电池状态信息预测的问题，其锂电池模型仍以机理模型为主，并不是完全根据所得数据通过系统辨识得到锂电池的模型参数。

为了克服传统基于模型驱动的机理建模的局限性，本文通过锂电池放电过程的时间序列数据采用EM 算法建立锂电池的随机动态模型。利用本文所提算法建立的模型能够有效的契合实验数据，能够保证建模误差稳定有界。

1 基于EM 算法的锂电池随机动态系统建模

1.1 锂电池随机动态系统模型

假设锂电池随机动态系统模型为带高斯白噪声的线性时变离散状态空间方程，且描述如下：

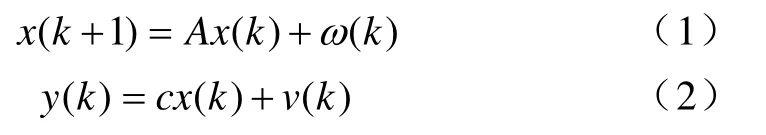
式中，状态变量x(k)为n×1 维向量，观测变量y(k)为n×1 维向量，ω(k)和v(k)分别为零均值的高斯白噪声过程噪声序列与测量噪声序列，A为系统状态转移矩阵，C为观测矩阵。

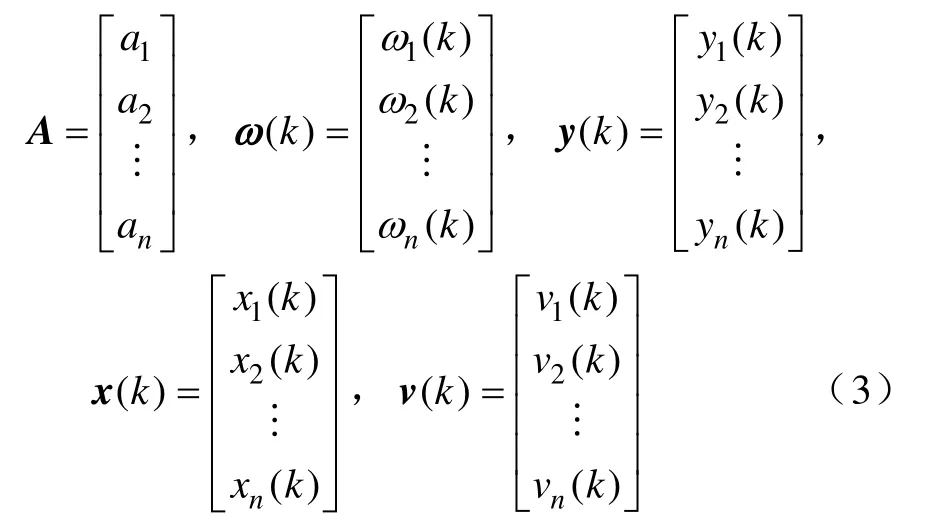
且ω(k)和v(k)协方差阵为

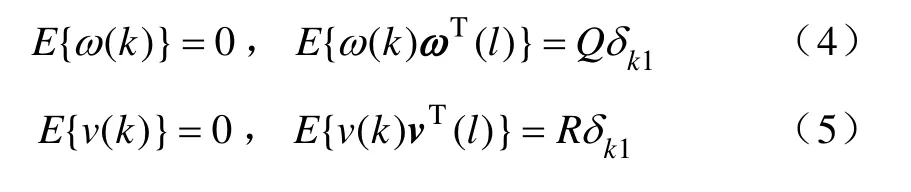
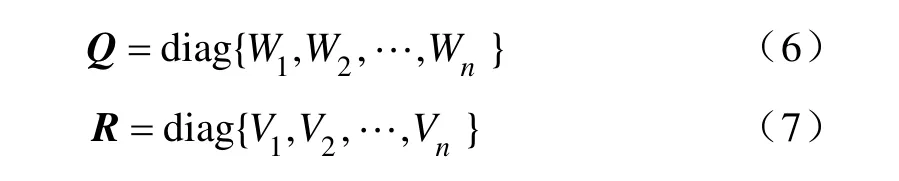
其中Q，R为均方差阵，δk1为Kronecker 函数。

在提出下文算法之前，定义系统所有待估参数为如下向量：

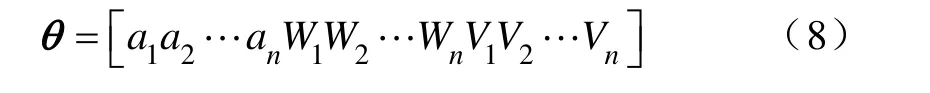
1.2 EM 算法简介与推导

EM（最大期望，Expectation Maximization）算法在时间序列模型当中的应用最早由Shumway 和Stoffer[8]于1982年提出，是计算一组参数的极大似然估计的通用迭代方法。实践证明：利用EM 算法进行参数估计在不同的信号处理应用上均能进行有效的计算[9-10]。

EM 算法在每一次迭代过程中被分成两步，其中包含一个E 步（期望步，Expectation Step）和一个M 步（极大似然步，Maximum Likelihood Step）。E 步通过观测数据和当前估计参数，估计完全数据对数似然函数，M 步通过极大化对数似然函数求得一组新的参数估计，所得新的参数估计值用于下一轮E 步的计算，如此循环迭代实现算法。

通过给定的观测向量Y和当前参数估计值，本文定义完整数据的对数概率密度函数的条件期望如下：

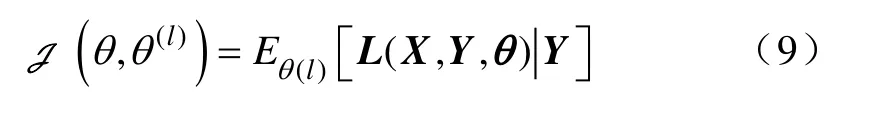
且

式中，C为独立于θ的常数。

新的参数估计如下：

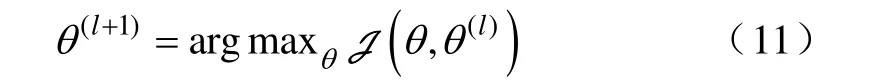
式中，l为迭代次数。

通过极大化J(θ,θ(l))能够获得新的参数估计θ(l+1)，即分别对ai，Wi-1和Vi-1求偏导可得新的估计参数为[11]

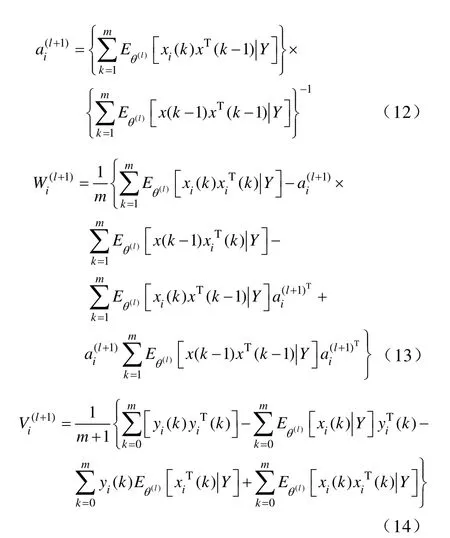
在给出Kalman 算法之前本文给出如下定义：

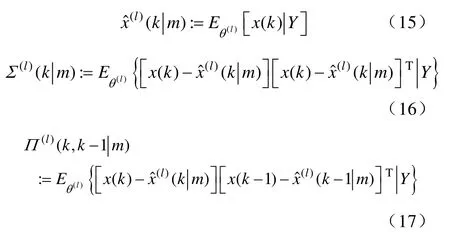
且

1）向前递归（滤波）：取k=1,2,…,m时间更新：

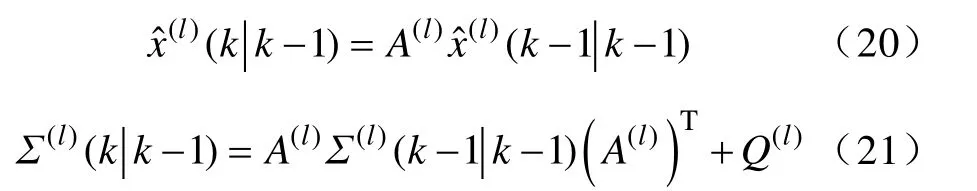
状态更新：

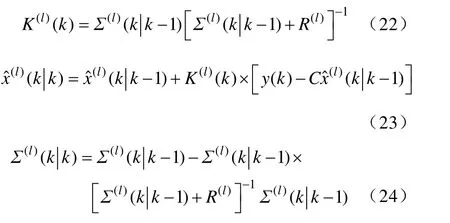
2）向后递归（平滑）：取k=m,m-1,…,1

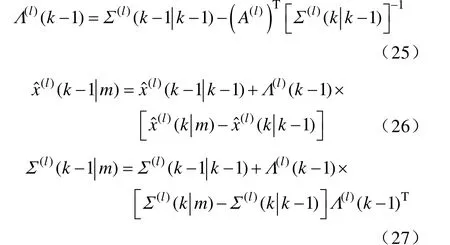
且

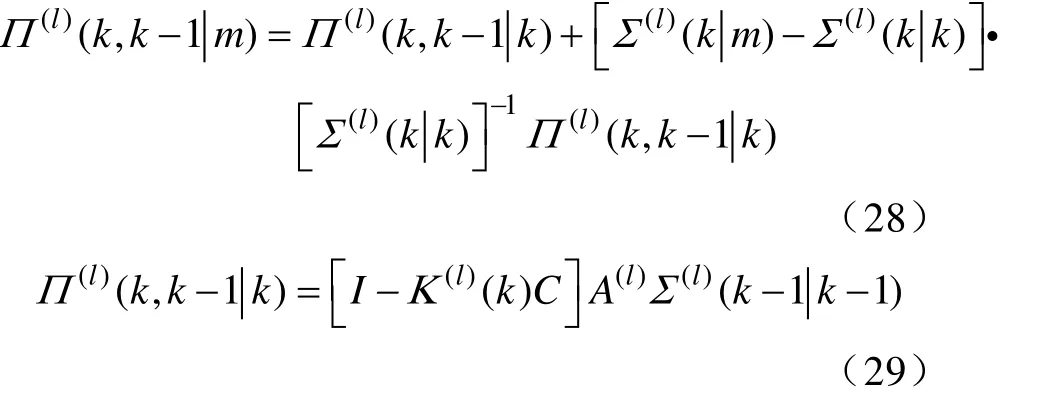
2 实验结果与分析

2.1 实验结果

本文采用锂电池的一次放电过程数据进行锂电池随机动态模型的构建与参数估计，数据来源于美国爱达荷州国家实验室对第二代18650 型号的锂电池进行的生命循环测试，测试在不同的温度、荷电状态以及压力条件下锂电池充放电过程中的电压电流等数据[13]。

通过本文所提出的算法对锂电池放电过程结合锂电池电压、电流、温度进行动态建模，可获得锂电池模型的状态转移矩阵A：

锂电池模型过程噪声协方差阵W为

锂电池模型测量噪声协方差阵V为

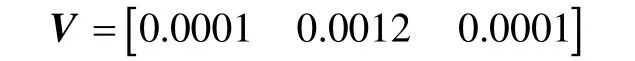
综上所说，通过本文所提算法能够有效的获得锂电池的随机动态模型参数。

锂电池实际放电过程中测量的电压和电流曲线和通过本文算法建立的随机动态模型下的锂电池电压和电流参数估计曲线如图1、图2所示，两者之间的误差曲线如图3和图4所示。

图1 电压测量值与模型估计值对比

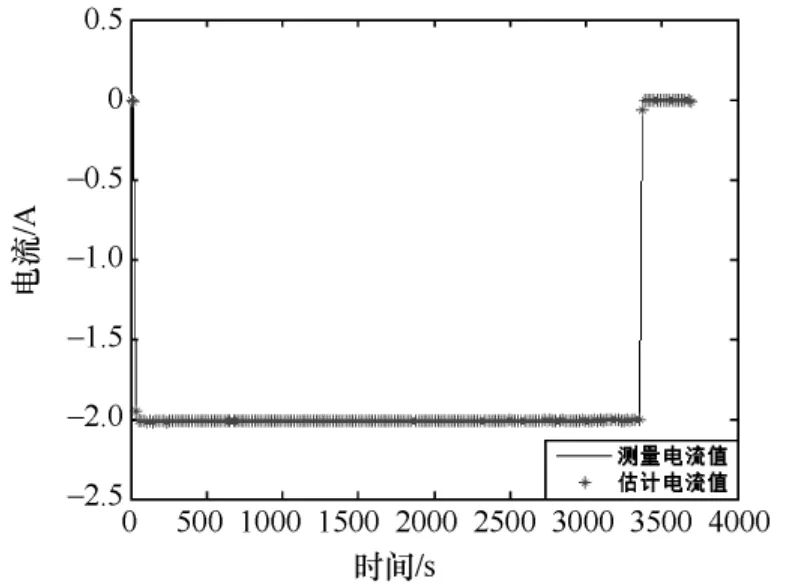
图2 电流测量值与模型估计值对比

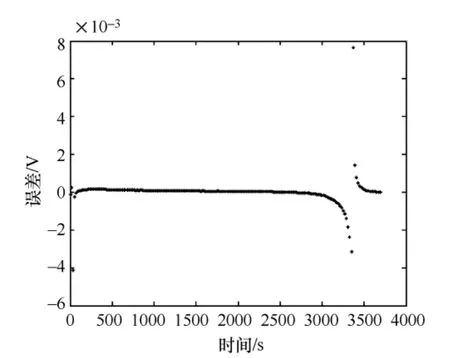
图3 电压测量值与模型估计值误差

图4 电流测量值与模型估计值误差

从图中可以看出基于EM 算法建立的锂电池模型能够很好的估计锂电池的状态值且误差小。

2.2 模型质量分析

从本文所选取的三组实验数据可得，锂电池的随机动态模型的估计协方差W很小，意味着所建的模型能够很好的契合实验数据。测量协方差阵V代表测量信号值的质量。

为了验证本文所提模型的稳定性和鲁棒性，需要计算模型状态转移矩阵的特征根，其特征根如下：

显然，所有的特征根都在单位圆内，因此本文所建的模型具有良好的稳定性和鲁棒性。

3 结论

本文基于锂电池放电过程的时间序列数据利用EM 算法实现了锂电池随机动态模型的构建。通过引入EM 算法，模型参数与电池的状态能够被同时识别。通过引入三组锂电池放电过程时间序列数据证明了本文所提算法的有效性。本文还提出了一些性能指标证明所推导的模型能够较好的契合实验数据。本文基于数据驱动的思想建立了锂电池的随机动态系统模型，通过所建立的模型能够较好的估计电池的状态参数，为锂电池的建模方式提供了另一种参考。

[1] Saha B,Goebel K.Modeling Li-ion battery capacity depletion in a particle filtering framework[C] Proceedings of the annual conference of the prognostics and health management society.2009: 1-10.

[2] Rao R,Vrudhula S,Rakhmatov D N.Battery modeling for energy aware system design[J].Computer,2003,36(12): 77-87.

[3] Budde-Meiwes H,Kowal J,Sauer D U,et al.Influence of measurement procedure on quality of impedance spectra on lead-acid batteries[J].Journal of Power Sources,2011,196(23): 10415-10423.

[4] Li J,Mazzola M,Gafford J,et al.A new parameter estimation algorithm for an electrical analogue battery model[C] Applied Power Electronics Conference and Exposition (APEC),2012 Twenty-Seventh Annual IEEE.IEEE,2012: 427-433.

[5] Hu Y,Wang Y Y.Two Time-Scaled Battery Model Identification With Application to Battery State Estimation[J]

[6] Kozlowski J D.Electrochemical cell prognostics using online impedance measurements and model-based data fusion techniques[C].Aerospace Conference,2003.Proceedings.2003 IEEE.IEEE,2003,7: 3257-3270.

[7] Goebel K,Saha B,Saxena A,et al.Prognostics in battery health management[J].IEEE instrumentation ＆ measurement magazine,2008,11(4): 33.

[8] Shumway R H,Stoffer D S.An approach to time series smoothing and forecasting using the EM algorithm[J].Journal of time series analysis,1982,3(4): 253-264.

[9] Weinstein E,Oppenheim A V,Feder M,et al.Iterative and sequential algorithms for multisensor signal enhancement[J].Signal Processing,IEEE Transactions on,1994,42(4): 846-859.

[10] Ziskind I,Hertz D.Maximum-likelihood localization of narrow-band autoregressive sources via the EM algorithm[J].Signal Processing,IEEE Transactions on,1993,41(8): 2719-2724.

[11] Wang Z,Yang F,Ho D W C,et al.Stochastic dynamic modeling of short gene expression time-series data[J].NanoBioscience,IEEE Transactions on,2008,7(1): 44-55.

[12] Ghahramani Z,Hinton G E.Parameter estimation for linear dynamical systems[R].Technical Report CRG- TR-96-2,University of Totronto,Dept.of Computer Science,1996.

[13] Saha B,Goebel K,Battery Data Set.http://ti.arc.nasa.gov/ project/prognostic-data-repository.