冲击电晕模型下的1000kV输电线路雷电 过电压分析

杨海龙 李荷薇 文 艺 雷 浩 陈 鑫

（1.西华大学电气信息学院,成都 610039；2.国网四川检修公司雅安运维分部，四川 雅安 625000； 3.国网攀枝花供电公司，四川 攀枝花 617000）

特高压电网具有输电距离远、送电容量大、线路损耗低、相对节省工程建设投资等优点，对我国电力资源的优化配置和国民经济可持续发展占有特别重要的意义，又因为1000kV 输电线路是远距离输电电网的骨架，在电力网络中占有极其重要的地位[1]。据统计表明雷击是引起输电线路跳闸的主要原因[2-3]，一但雷击1000kV 输电线路引起跳闸，将威胁到电力系统的安全稳定运行。所以研究由雷击引起的输电线路电磁暂态过程，对分析线路的耐雷水平和雷电过电压具有十分重要的现实意义。雷击输电线路特别是超高压等级及以上输电线路时由于线路频变参数和冲击电晕效应对波过程的影响，使雷电侵入波发生了衰减和变形，并沿线形成一个电晕套，相当于增大了导线的半径，而这种现象随电压等级的升高变得越来越明显。

雷电冲击波沿输电线路传播一旦发生电晕，会改变冲击波的波形和幅值，这种冲击电晕不但在1000kV 特高压输电线路耐雷水平的研究中，而且在输电线路设计、建设以及研究变电站防雷保护方案和进行电气设备冲击绝缘配合中都应当考虑的重要因素。然而，在现有电晕模型中，大多未考虑各相导线间的耦合作用，这些模型用于仿真是有误差的也不精确。本文建立了一种更加符合工程实际情况的电晕模型，对1000kV 输电线路雷电过电压进行了仿真分析。

1 冲击电晕仿真模型的建立

1.1 电晕的库-伏（q-u）特性

冲击电晕的伏库特性是指导线上冲击电压的瞬时值u与导线及其周围电晕套内的总电荷q的关系。它是研究冲击波衰减变形的基础，典型的伏库特性曲线成回环状，如图1所示[4]。OA 段对应于波头部分，伏库特性曲线呈直线其斜率等于导线的几何电容；AB 段对应于波头的电晕发展阶段，当电压u超过U0以后开始出现电晕，导线周围聚集起空间电荷，伏库特性曲线呈非线性上翘来模拟导线的动态电容；BC 段对应波尾部分，由于空间电荷还来不及迁移和扩散，因此它几乎与OA 段平行。我们对电晕的研究通常只研究非线性变化的伏库特性上升分支曲线AB 段。

图1 q-u 特性曲线

1.2 电晕的等值电路模型

冲击电晕使交流输电线路的等值半径和对地电容均发生了变化如图2所示。传统电晕模型忽略了导线间耦合系数变化影响。而本文在已有模型的基础之上，结合电晕效应伏库特性的特点，对原有电晕模型进行了改进，考虑了导线间耦合系数，使改进后的电晕模型更加符合实际情况。

图2 起晕时导线对地电容

由于电晕空间电荷在导线周围形成的电晕套径向导电性能较好，但轴向电导甚小，可以认为发生电晕以后线路纵向电流仍然集中在导线中，电晕未改变输电线路的磁场分布。换句话说就是冲击电晕没有影响到线路电感参数，只有交流输电线路的等值半径和对地电容参数发生了变化，在研究雷电过电压下的冲击电晕时电导[5]是可以忽略的。由图2可知，输电线路起晕时输电导线和大地之间的电容可以看作主要由Cdcor和Ca两部分电容的串联。输电线路发生电晕以后线路导纳将随电压而变化，阻抗随频率而变化这使得对雷电过电压的研究变得复杂，本文采用的仿真将两者结合了起来，建立了一个更完整的输电线路仿真电晕模型。整个仿真同时考虑了线路阻抗的频变参数。通过仿真，对于雷电波在输电线路中传播的暂态过程有了进一步的认识。下面给出了三相输电线路传统电晕等值电路见图3和改进后的电晕等值电路图4。图4中Cab、Cbc、Cac分别为电晕效应引起的各相导线间耦合电容；Cf1为导线半径r到电晕套边缘等值半径rcor间空气电容，Cf2为电晕套边缘等值半径rcor到大地间的空气电容；Lh和Rh的串联旨在为电晕支路中提供模拟电晕放电所需时延；U0为导线电晕起始电压值。虚线框内为导线电晕模型等值电路。

图3 三相交流输电线路的传统型电晕等值电路

图4 三相交流输电线路的改进型电晕等值电

2 电晕参数计算

2.1 电晕电容和起始电压、场强

当雷击线路时，线路电压达到电晕起始电压值前，U小于U0，二极管无法导通呈断开状态，电晕模型中仅有Cf1和Cf2串联组成导线对地几何电容，模拟线路伏库特性OA 段；当线路电压达到电晕起始电压值时U大于等于U0时，二极管导通电晕支路加入到电晕模型之中，此时线路对地的动态电容为Cdcor和Cd0的并联，电晕电容的值由下式可得

式中，U为电晕状态下线路上的电压；U0线路上的起晕电压为电晕损耗常数。

电晕起始电压U0的计算方法。根据静电场理论可以计算导线电压与导线表面最大场强的关系。当导线表面场强达到电晕起始场强时，导线即开始发生电晕。电晕起始场强[6]E0可由皮克公式求出

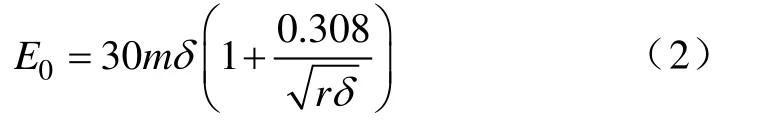
式中，r是导线半径，cm；δ为相对空气密度系数，m为导线表面粗糙系数,对于绞线m=0.82。根据电晕起始场强E0，又知道导线对地的平均悬挂高度h，导线的电晕起始电压U0可按以下各式计算。

分裂导线电晕起始电压的值为[7]

式中，n为分裂导线数；E0为起晕场强；A为分裂间距（A=d/(2sin π/n)，d为相邻两根分裂导线的距离）；分裂导线等效半径

2.2 导线相间耦合系数与耦合电容

雷电过电压波作用在高压输电导线时，当导线电压大于起晕电压时，各导线相间耦合系数将增大。起晕导线周围的空间电荷也将使各相间耦合电容增大。当输电线路不起晕时，线路的几何电容确定了相间耦合电容，相间耦合系数即是线路几何耦合系数[8-9]。下面简要介绍了耦合系数和耦合电容的计算公式。

输电线路电位系数矩阵和波阻抗矩阵如式（4）所示：

各相导线自波阻抗与互波阻抗为式（5）和式（6）：

各相导线自电位系数与互电位系数为式（7）和式（8）：

式中，ε0、μ0分别为真空中的介电常数和磁导率常数；hi为各相导线对地高度；Hij为各相导线与其他导线镜像之间的距离；Dij为各项导线之间的距离。

考虑冲击电晕影响后导线的等值波阻抗计算公式如式（9）所示：

式中，u为导线上的工作电压；Z0为几何波阻抗；正极性时，常数M=1.36，负极性时，M=1.13。根据式（9）可求出冲击电晕状态下的自波阻抗，再将结果代入式（10）可得到电晕时线间耦合系数。

式中，Ymm为线路波阻抗矩阵[Z]3第m行第m列的代数余子式。

电晕引起的相间耦合电容为

表1 1000kV 交流输电线路电晕计算参数

3 仿真各元件模型的建立

3.1 雷电流模型

本文采用2.6/50μs 的双指数函数雷电流。这是目前使用最广泛的雷电流模型，它能够直接、简单的进行积分和微分的数学变换，而且能够反映出雷电流的主要参数。

3.2 杆塔模型

特高压杆塔高，为了反映雷电波在杆塔的传播过程，本文采用了分级传输塔和接地阻抗相结合的多波阻抗模型[11-12]。如图5所示。

图5 1000kV 输电线路杆塔及其多波阻抗模型

分级传输塔每部分包括一段分布参数的无损线和阻尼电阻和阻尼电感的并联支路，该并联支路体现了波在杆塔中的衰减现象。Yamada 等运用直接测量法测量杆塔各参数，并推导出阻尼电阻Rti和阻尼电感Lti的计算式式（12）、式（13）、式（14）：

式中，Zti为塔波阻抗；h1、h2、h3具体指代如图5所示；v为光速；γ为衰减系数；φ为阻尼系数。在杆塔模型中Zt1=Zt2=220Ω，Zt3=150 Ω阻尼系数φ=1衰减系数γ =0.7[11]。

3.3 输电线路模型

根研究表明，当线段长度由200m 变化到100m时，对计算结果有影响；当线路每段长度100m 变化到50m 时，对计算结果几乎没有影响[13-14]，所以在对三相交流单回输电线路作电晕研究时，沿线路每隔100m 加入上述电晕模型。本文采用ATP-EMTP自带的计及频变参数的LCC/Jmarti 模型该模型考虑了输电线路参数的频变特性，且该模型已计算了导线和避雷线的几何参数，提高了计算精确度。

3.4 绝缘子闪络模型

闪络模型中计及了冲击电晕的影响，使其更能反映实际的情况。采用ATP 软件中的压控开关来模拟缘子串的闪络，U50%的放电电压取4MV[15]，这种开关在正常情况下处于开断状态，只有当暂态过程中开关触头间的作用电压超过给定的放电电压时，开关闭合即绝缘子串两端的过电压超过绝缘子串的U50%绝缘子串闪络。

4 仿真结果及分析

4.1 各种模型的仿真电路

通过前面选择的模型，为接下来的仿真奠定了基础，下面将对雷电流源绕击导线A 相三种模型进行仿真电路的搭建如图6、图7、图8所示。

仿真电晕线路的基本思想就是将电晕等效为一组非线性支路，使此支路能够体现电晕的伏库特性，并且将输电线路分成若干小段，在分段节点上接入非线性电晕支路，这样建立起电晕线路的仿真模型。

图6 无电晕模型仿真电路

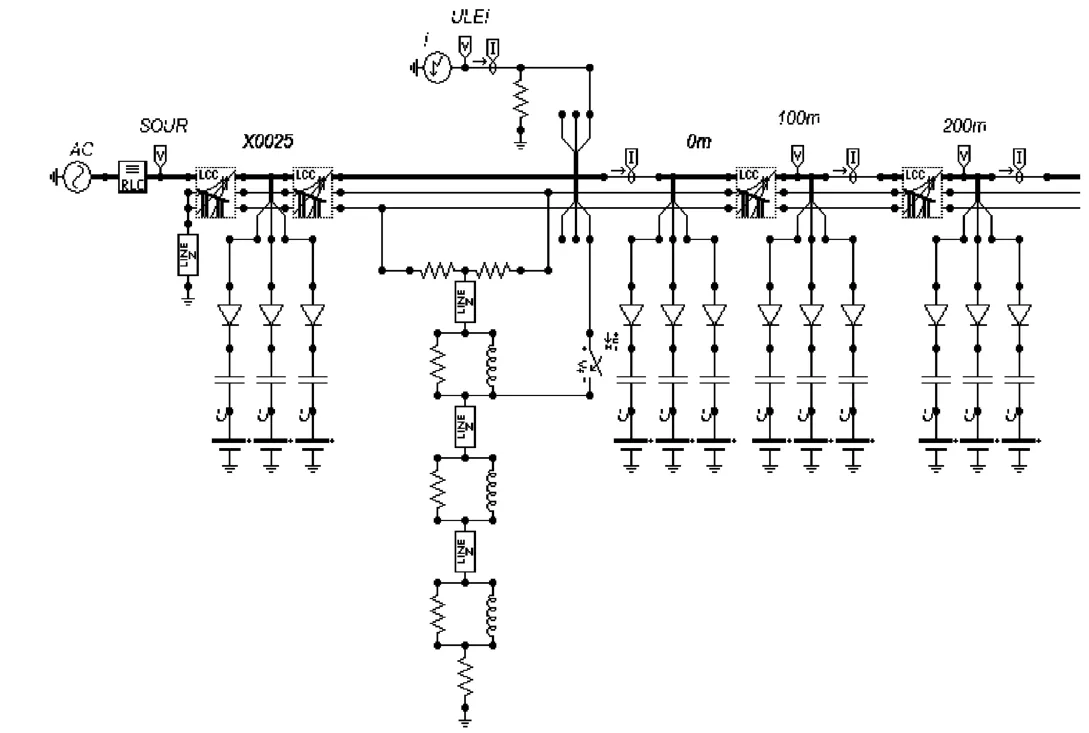
图7 传统电晕模型仿真电路

图8 改进电晕模型仿真电路

4.2 仿真波形分析

按照上图搭建的仿真模型并进行仿真，电流源取40kA；闪络电压4MV；线路初始拟合频率0.01Hz可以得到冲击电晕下的1000kV 输电线路雷电过电压不同状态下的波形如图9所示。

图9 雷电过电压波形

当雷绕机输电线路A 相时，雷击点不同,距离不同，采用的电晕模型不同，得到雷电过电压的波形也就不同。由于冲击电晕发生以后线路电容随电压提高而增大，有电晕线路的波阻抗将会减小，因而影响导线间的耦合系数，会使电压、电流波形与不计电晕时的情况有所不同。图9（a）雷击1000kV交流输电线路100m 处时，从图中可以看出考虑电晕时线路上A 相雷电压的幅值比不考虑电晕时要低。这是因为发生电晕时使线路电容增大，分压作用增强，加之雷电过电压波形发生了衰减和变形。从图9（c）和图9（g）看出，由于改进电晕模型电感和电阻组成的支路的时延作用使得电晕发生时间滞后于传统模型时的起晕时间，改进模型比传统模型过电压波形幅值出现时间要提前些，还可以从图9（a）中看出无电晕模型杆塔绝缘子发生了闪络，导致电压波形陡降接近于零。图9（b）和图9（f）表明计及电晕效应时，线路A 相电流幅值随着与雷击点距离的增大而减小，这是由于电晕要消耗过电压波的能量。图9（d）和图9（h）表明改进模型中有相间耦合时过电压幅值比无相间耦合时小，改进模型中有相间耦合时线路电流比无相间耦合时小，这是由于输电线路有电晕以后的动态电容大于几何电容，就使雷电波的相速度减缓而造成时延，同时使得线路波阻抗减小，耦合系数变大。这些因素的综合作用引起了雷电过电压波形的变化进而导致上述现象的发生。

5 结论

通过ATP-EMTP 建立冲击电晕模型对1000kV输电线路雷电过电压进行分析，运用能够反映电晕伏库特性的线路模型，这样就能考虑到雷电波在节点的折、反射以及雷电波与相邻线路之间的互耦的情况，并且对传统电晕模型进行了改进，考虑了导线间耦合系数变化的影响，使计算结果更精确。通过雷电过电压波形分析我们可以得出：冲击电晕发生以后线路电容随电压提高而增大，有电晕线路的波阻抗会减小，耦合系数增大，这样使得线路上的过电压波形发生严重衰减和变形，降低了雷电过电压的幅值，由仿真可知耐雷水平提高了15%左右。这显著提高了特高压交流输电线路的运行的稳定性。仿真结果对特高压输电线路设计、建设和运行以及研究变电站防雷保护方案和进行电气设备冲击绝缘配合方面提供了参考。

[1] 袁清云.特高压直流输电技术现状及在我国的应用前景[J].电网技术,2005,29(14): 1-3.

[2] 黄瑞梅.输电线路防雷接地技术研究[J].水电能源科学,2009,27(5): 207-210.

[3] 李晓岚,杜忠东.1000kV 特高压输电线路防雷问题探讨[J].高电压技术,2006,32(12): 52-54.

[4] 陈梁金,杜斌,刘青,等.计及雷击电晕时750kV 进线开关触头间暂态过电压的研究[J].高压电器,2004,40(3): 167-169.

[5] 刘磊,李敏,李锐海,等.高海拔特高压直流试验线路电磁环境初步试验研究[J].南方电网技术,2010,4(6): 49-53.

[6] 尤少华,刘云鹏,律方成,等.不同海拔下电晕笼分 裂导线起晕电压的计算分析[J].中国电机工程学报,2012,32(4): 169-177.

[7] 袁海燕,傅正财,魏本刚,等.冲击电晕对特高压输电线路绕击耐雷水平的影响分析[J].中国电机工程学报,2009,29(25): 111-116.

[8] 戴玉松,颜怀梁.考虑冲击电晕时的一种多相线等值电路模型[J].中国电机工程学报,1997,17(5): 339-343.

[9] Lee K C,Hydro B C.Non-linear corona models in an electromagnetic transients program (EMTP)[J].IEEE Transa-itions on Power Apparatus and Systems,1983,102(9): 2936-2942.

[10] Marti J R,Castellanos F,Santiago N.Wide-band corona circuit model for transient simulations[J].IEEE Transactions on Power Systems,1995,10(4): 1003- 1013.

[11] 张永记,司马文霞,张志劲.防雷分析中杆塔模型的研究现状[J].高电压技术,2006,32(7): 93-97.

[12] 樊争亮,常美生.杆塔模型对1000kV 特高压同塔双回线路反击过电压的影响[J].电力学报,2013,28(2): 104-107.

[13] 杨庆,王荆,陈林,等.计及冲击电晕的输电线路雷电绕击和反击智能识别方法[J].高电压技术,2011,37(5): 1149-1157.

[14] Carneiro S Jr,MartiJ R.Evaluation of Corana and Line Models in Electromagnetic Transients Simulations[J].IEEE Transactions on Power Delivery,1991,6(1): 334-340.

[15] 李翔,赵全江,刘文勋,等.1000kV 特高压交流大跨越线路设计[J].高电压技术,2010,36(1): 265- 269.