惯性测量组合减振系统动力学分析及实验研究
2015-05-28郑玲房占鹏
郑玲,房占鹏
(重庆大学 机械传动国家重点实验室,重庆 400030)
惯性导航系统(IMU)的工作情况直接影响导航的精度和可靠性。由于IMU的工作环境具有振动加速度大、激励频率范围广和受激励时间长等特点,为了保证IMU的工作精度和可靠性,通常使用隔振器对IMU进行隔振[1—3]。因而,为了隔离来自载体强烈的振动和冲击,使测量组合具有良好的工作环境,确保IMU可靠、稳定的工作,必须设计高性能的减振系统[4—6]。
随着惯性导航技术的要求越来越高,研究人员也越来越重视IMU减振系统设计的研究。姚建军等[7—8]分别建立了5种不同隔振模式的惯性导航系统动力学微分方程,通过对IMU在6个自由度上振动耦合特性和传递特性的对比分析,提出了不同隔振系统的布置方式。刘世品[9]采用有限元的方法对橡胶隔振器的结构进行了修改,分析了此隔振系统的频率响应,搭建了试验测试系统平台,实验验证了建立的有限元模型的正确性和分析方法的有效性。Steinberg等[10—11]为了探讨电子设备的减振和隔振方法,采用理论分析对电子设备的振动和冲击等问题进行了研究。
文中对IMU的减振系统进行了动力学特性研究。建立了测量组合的三维模型,为了提高IMU的解耦率,调整IMU和支架的质心,使IMU的质心与4个隔振器的刚度中心基本重合。采用Mooney-Rivlin超弹性本构模型对橡胶隔振器的橡胶材料进行表征,并确定了橡胶材料的超弹性本构模型的参数,进而建立了IMU减振系统有限元模型。分析了减振系统的频率响应和冲击响应,并对IMU减振系统进行了振动和冲击试验。
1 IMU振动系统解耦
振动解耦可以使IMU系统各个自由度上的振动相对独立或分离,这样可在不影响其他自由度的情况下对隔振效果不佳的自由度独立采取措施,使IMU获得良好的振动姿态,有利于提高隔振性能。
IMU减振系统隔振器布置方式如图1所示,理论上IMU减振系统在各自由度方向上的振动是互不干涉、互不耦合的,因而,可按照单自由度振动系统对IMU减振系统进行设计。在实际设计时,很难做到IMU质心与隔振器刚度中心的重合,振动系统在各自由度方向上具有振动耦合,因此,需对IMU减振系统进行解耦分析。
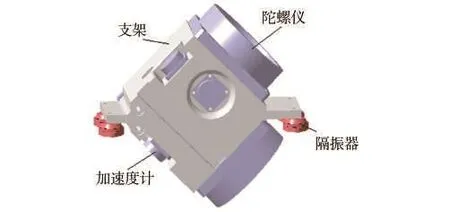
图1 IMU减振系统结构Fig.1 The vibration system model of IMU
1.1 振动系统解耦的原理
建立IMU减振系统的动力学模型,由于IMU是通过4个隔振器安装到运载体上的,因而,可将IMU减振系统看作一个悬置系统,如图2所示。G0-XYZ为定坐标系,支架和测量组合静平衡时的质心在原点G0处。相对于定坐标系G0-XYZ的是动坐标系G-xyz。系统的广义坐标为IMU减振系统沿X,Y,Z三个方向的平动坐标x,y,z和围绕x,y,z轴转动的坐标θx,θy,θz,即{q}={x,y,z,θx,θy,θz}T。

图2 振动系统动力学模型Fig.2 The model of vibration system
无阻尼情况下,系统的动力学方程为:

式中:[M],[K]分别为系统的质量矩阵和刚度矩阵:

式中:Ixx,Iyy,Izz和Ixy,Iyz,Izx分别为振动系统绕坐标轴X,Y,Z的转动惯量和惯性积;kxx,kyy,kzz和kαα,kββ,kγγ分别为振动系统绕坐标轴X,Y,Z的总往复刚度和总回转刚度;kmn(m≠n)为系统的耦合刚度。
根据振动理论,该振动系统的动力学方程的解可表示为:

将式(4)代入振动系统的动力学方程可得:

通过求解方程式(5)可得到振动系统的固有频率ωi和主振型{Xi}(i=1,2,3,4,5,6)。
在坐标系G0-XYZ中,可以得到振动系统在各阶次主振动时的能量分布矩阵。当系统在第k阶模态振动时,此矩阵为:

式中:ωk为k阶固有频率。
振动系统在第k阶模态振动时,分配到第i个广义坐标上能量的总和占整个振动系统总能量的百分比为:
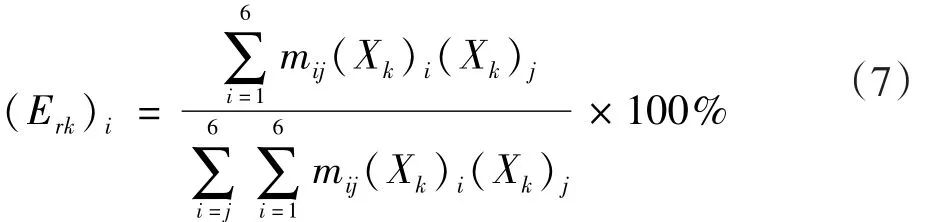
当(Erk)i=100%时,说明第k阶模态振动能量全部集中在第i个广义坐标上,其他自由度上没有振动能量,即不发生振动,这就实现了解耦。
1.2 IMU质心位置调整
在理想状态下,IMU的质心和隔振器的刚度中心完全重合,IMU在6个自由度上的振动完全解耦。对于初始设计的结构,系统的质心和隔振器的刚度中心之间具有3.2 mm的偏差。因而,需要通过调整陀螺仪和加速度计的位置以及支架结构尺寸,使IMU的质心与隔振器的刚度中心基本重合,进而使IMU在各自由度上的振动都具有很高的解耦率。
在三维软件Catia中,输入各个部件的材料参数,对陀螺仪和加速度计的位置以及支架的结构尺寸进行调整。文中使用的4个隔振器的规则相同,并且每个隔振器在空间三向具有相同的刚度,所以4个隔振器安装点坐标的平均值即是刚度中心坐标。调整后IMU质心的坐标为(104.87,97.173,-96.15),4个隔振器刚度中心的坐标为(105,97,-96),两坐标的差值为(0.13,0.173,0.15)。可以看出,装配体的质心和隔振器的刚度中心基本实现了完全重合。
1.3 调整前后解耦率的对比
调整前后IMU减振系统的振动解耦率见表1和表2。通过对比分析可知,对IMU调整之前,振动解耦率较低,IMU的振动会出现耦合。在IMU调整后,在各阶模态上的振动解耦率都有很大的提高。其中,一、五、六阶模态实现了完全解耦,二、三、四阶模态的解耦率也都大于80%,有助于使IMU在各个方向上都获得良好的减振效果。
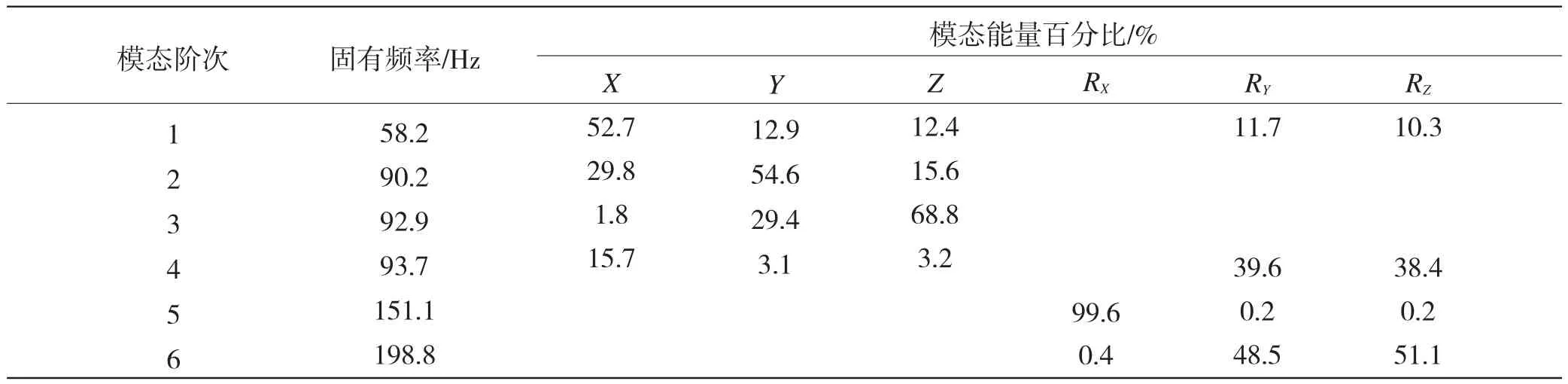
表1 调整前解耦率Table 1 Decoupling rate before adjustment

表2 调整后解耦率Table 2 Decoupling rate after adjustment
2 橡胶材料表征模型的分析
选用的橡胶隔振器如图3所示,它由上支座、下支座以及隔振橡胶组成。上支座连接IMU,下支座与载体连接,起到安装和支持的作用。锥形的硫化橡胶件是主要的减振元件,为了防止橡胶件发生脱落,将金属件嵌入到凸出的两个圆环中从而加强胶合。为了对IMU减振系统进行振动响应和冲击响应仿真分析,需要对橡胶材料进行表征。

图3 隔振器结构Fig.3 The sketch of damper
2.1 橡胶材料的表征模型
橡胶材料是一种具有非线性、超弹性的各向同性近似不可压缩材料。基于应变能密度函数的大弹性变形本构理论[12]是描述超弹性材料特性的有效理论之一,根据超弹性本构关系模型,应变能密度函数采用的多项式形式表示为[13]:
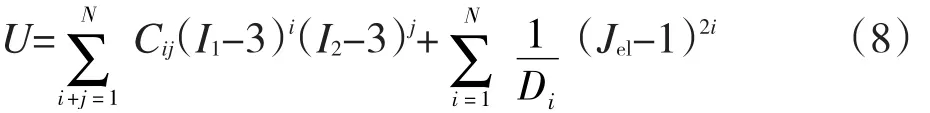
式中:N是项数;Cij和Di分别用来描述橡胶材料的剪切特性和可压缩性;I1,I2分别是第一、第二偏应变不变量;Jel是弹性体积比。当项数为1时,式(8)可转化为:

采用Mooney-Rivlin超弹性本构模型对橡胶材料进行表征,只需要确定橡胶材料的相关系数C10,C01和D1,橡胶材料的弹性特性即可得到表征。橡胶材料系数与初始剪切模量G0和体积模量K0的关系为[10]:
2.2 橡胶材料本构模型材料系数的确定

采用实验的方法[13]确定Mooney-Rivlin模型材料系数较为复杂,提高了减震器的设计成本和难度。橡胶的超弹性材料系数C01/C10和邵氏硬度之间的经验关系如图4所示,根据图4可以初步确定其相关的材料系数[14]。

图4 C01/C10与邵氏硬度的经验关系Fig.4 Empirical relationship between C01/C10and HS
根据式(10),橡胶材料的等效弹性模量E以及等效剪切模量G与系数C10,C01的关系为[15]:

对于确定硬度的橡胶材料,可通过图4确定C01/C10值,代入到式(11)中,可求解出C01,C10。设橡胶材料的参数D1为0,邵氏硬度为36°,根据图4和式(11)可确定的材料系数为:C01=0.0164,C10=0.1825,D=0。
3 IMU减振系统振动和冲击试验仿真分析
3.1 有限元模型的建立
在商业有限元软件HyperMesh中,采用六面体单元对IMU减振系统划分网格,划分的单元总数为132 508个。采用刚性接触定义各个接触面,并且对隔振器安装面上的自由度进行全约束,建立的IMU减振系统的有限元模型如图5所示。把建立的有限元模型导入到ABAQUS中进行计算分析。
对建立的有限元模型进行分析时,结构阻尼采用复合阻尼,其表达式为:

图5 IMU隔振系统的有限元模型Fig.5 The FEM model of the IMU vibration system

3.2 频率响应仿真分析
在有限元软件ABAQUS中对建立的有限模型进行频率响应分析,求解方法为模态叠加法,分别在4个隔振器安装面的X,Y,Z三个方向上施加幅值为0.5g,频率为10~500 Hz的加速度基础激励。分析IMU在X,Y,Z三个方向上的加速度响应,其频率响应曲线分别如图6所示,其中,T为传递率。
通过分析图6,IMU减振系统在X,Y,Z三个方向上的固有频率分别为:93.2,92.5,94.1 Hz,等效阻尼比处于0.166~0.172之间,放大倍数在X,Y,Z三个方向上分别为3.072,3.12,3.17。满足了IMU减振系统在三个方向上的刚度和阻尼相等的要求。
3.3 冲击响应仿真分析
在冲击响应分析时,对4个隔振器安装面的Z方向上施加冲击激励,冲击激励为55g的半正弦加速度激励,持续时间为11 ms,如图7所示。得到IMU上的加速度响应如图8所示。

图6 减振系统幅频响应曲线Fig.6 The frequency response curve

图7 冲击激励加速度Fig.7 The acceleration of shock excitation

图8 冲击加速度响应Fig.8 The acceleration of shock response
由图8可见,最大响应幅值为70.1g,响应被放大,其冲击传递率大于1。该系统固有频率在90 Hz以上,不能隔冲,如在此冲击激励条件下要得到较好的隔冲效果,需减小系统的固有频率。分析图9可得,隔振器最大压缩量为0.92 mm,比结构的预留空间2 mm要小很多,满足IMU的设计要求。

图9 隔振器的压缩量Fig.9 The deformed distance of isolator
4 IMU减振系统试验研究
根据相关的产品定型试验指标的要求,依据GJB 150.16—86《军用设备环境试验方法·振动试验》和GJB 150.18—86《军用设备环境试验方法·冲击试验》,分别对文中设计的IMU减振系统进行频率响应试验测试和冲击试验测试。
4.1 振动响应分析
在做频率响应测试试验时,采用电动振动实验系统对IMU进行激振。IMU通过隔振器和夹具固定在振动台台面上,响应信号采集点位于IMU上顶部,测量响应点处的加速度响应。试验测试时,采用对数扫频的方式,扫频速率为1 oct/min,扫频范围为5~500 Hz,分别对振动台在X,Y,Z三个方向上施加正弦加速度激励,激励幅值为0.2g。IMU减振系统的试验和仿真的谐振频率和放大倍数见表3。
从表3中可以看出,减振系统在X,Y,Z三个方向上谐振频率在90.79~92.91 Hz之间,放大倍数在3.12~3.42之间,试验验证了建立的有限元模型的正确性和设计系统的有效性。

表3 隔振器固有频率试验与仿真对比值Table 3 The comparison of experiment and simulation in vibration
4.2 冲击响应分析
冲击试验中,冲击激励是峰值为55g的半正弦波,激励持续时间为11 ms,冲击激励方向为Z向,得到的加速度响应如图10所示。在试验完成后,隔振器没有出现结构损伤,测量得到的最大加速度响应峰值为72.47g,与数值计算值(71.3g)差别不大,说明了IMU减振系统在冲击响应谱作用下具有很好的冲击响应。

图10 冲击试验激励和响应曲线Fig.10 The excitation&response of the shock experiment
5 结论
文中对设计的IMU减振系统进行了动力学特性研究。主要结论如下。
1)建立了测量组合的三维模型,为了提高IMU的解耦率,调整IMU和支架的质心,使IMU的质心与4个隔振器的刚度中心基本重合。对比分析了IMU的质心调整前后的解耦率,调整质心后,IMU的解耦率大大提高,使各个自由度的解耦率都在80%以上。
2)采用Mooney-Rivlin超弹性本构模型对橡胶隔振器的橡胶材料进行表征,并初步确定了橡胶材料本构表征模型的相关参数。建立了IMU减振系统的有限元模型,并对IMU减振系统进行了频率响应分析和冲击试验分析。通过仿真分析,表明设计的减振系统满足空间减振的要求。
3)对IMU减振系统进行了振动响应试验和冲击响应试验,试验结果表明,设计的IMU减振系统满足了在3个方向上刚度和阻尼相等的要求。通过与仿真结果进行对比,验证了设计的IMU减振系统的有效性和有限元建模的正确性,为以后IMU减振系统的设计研究奠定了基础。
[1] 黄金威,杨朋军,于云峰,等.惯性平台橡胶隔振器弹性特性的有限元分析[J].机械设计,2006.23(11):51—54.HUANG Jin-wei,YANG Peng-jun,YU Yun-feng,et al.Finite Element Analysis on Elastic Characteristics of Rubber Shock Absorber of Inertia Platform[J].Journal of Machine Design,2006,23(11):51—54.
[2] 黄林,王寿荣,颜泽飞,等.惯性技术中集成控制减振的研究[J].中国惯性技术学报,1998,6(2):15—28.HUANG Lin,WANG Shou-rong,YAN Ze-fei,et al.Research of Integrated Control Devibration in Inertial Technology[J].Journal of Chinese Inertial Technology,1998,6(2):15—28.
[3] 秦洁,师永宁.金属丝网隔振器的研制与试验研究[J].装备环境工程,2013,10(2):109—112.QIN Jie,SHI Yong-ning.Development and Test of Metal Wire Net Isolator[J].Equipment Environmental Engineering,2013,10(2):109—112.
[4] 李晓波,吴斌,董程,等.捷联惯导减振系统的耦合振动研究[J].装备环境工程,2014,11(2):43—48.LI Xiao-bo,WU Bin,DONG Cheng,et al.Research on Coupled Vibration of Strapdown INS Damping System[J].Equipment Environmental Engineering,2014,11(2):43—48.
[5] 张生鹏,李晓刚.某橡胶减振垫加速贮存老化试验及寿命预测[J].装备环境工程,2010,7(5):24—28.ZHANG Sheng-peng,LI Xiao-gang.Accelerated Aging Tests and Storage Life Prediction for a Rubber Damping Pad[J].Equipment Environmental Engineering,2010,7(5):24—28.
[6] 王佳民,裴听国.惯性平台减振系统动力学分析及参数设计[J].战术导弹控制技术,2003,43(4):51—54.WANG Jia-min,PEI Ting-guo.Dynamic Analysis of Inertial Plat form Vibration-Reduced System and its Parameters Design[J].Control Technology of Tactical Missile,2003,43(4):51—54.
[7] 姚建军,付继波,刘道静.捷联惯导系统振动耦合特性研究[J].战术导弹控制技术,2005,49(2):55—58.YAO Jian-jun,FU Ji-bo,LIU Dao-jing.Coupled Vibration Characteristics of Strap down Inertial Navigation System[J].Control Technology of Tactical Missile,2005,49(2):55—58.
[8] 姚建军.捷联惯导系统不同隔振模式的比较[J].强度与环境,2009,36(2):19—27.YAO Jian-jun.Contrast of Different Vibration Isolation Patterns Used in Strap-down Inertial Navigation System[J].Structure&Environment Engineering,2009,36(2):19—27.
[9] 刘世品,曾祥国,黄光速,等.有限元频响分析在减振器设计中的应用[J].华中科技大学学报,2008,25(3):45—53.LIU Shi-pin,ZENG Xiang-guo,HUANG Guang-su,et al.The Frequency Response of Finite Element Analysis in the Application of Vibration Isolator Design[J].Journal of Huazhong University of Science and Technology,2008,25(3):45—53.
[10]BANERJEE K,DAM B,MAJUMDAR K,et al.An Improved Dither-Stripping Scheme for Strapdown Ring Laser Gyroscopes[C]//IEEE 2004 Region 10 Conference,Tencon:IEEE,2004.
[11]VEPRIK A M,BABITSKY V I.Vibration Protection of Sensitive Electronic Equipment[J].Harsh Harmonic Vibration,2000,238(1):19—30.
[12]上官文斌,吕振华.汽车动力总成橡胶隔振器弹性特性的有限元分析[J].内燃机工程,2003,24(6):50—55.SHANGGUAN Wen-bin,LYU Zhen-hua.Finite Element Analysis of Elastic Characteristics of Rubber Isolator for Automotive Powertrain Systems[J].Chinese Internal Combustion Engine Engineering,2003.24(6):50—55.
[13]费康,张建伟.ABAQUS在岩土工程中的应用[M].北京:中国水利水电出版社,2010.FEI Kang,ZHANG Jian-wei.Application of ABAQUS in Geotechnical Engineering[M].Beijing:China Water Conservancy and Hydropower Press,2010.
[14]任全彬,蔡体敏,安春利,等.硅橡胶“O”形密封圈Mooney-Rivlin模型常数的确定[J].固体火箭技术,2006,29(2):130—134.REN Quan-bin,CAI Ti-min,AN Chun-li,et al.Determination on Mooney-Rivlin model constants of Silicon Rubber"O"-Ring[J].Journal of Solid Rocket Technology,2006,29(2):130—134.
[15]王锐,李世其,宋少云,等.橡胶隔振器系列化设计方法研究[J].噪声与振动控制,2006,26(4):11—25.WANG Rui,LI Shi-qi,SONG Shao-yun.Research on Serialization Design Method of Rubber Vibration Isolators[J].Noise and Vibration Control,2006,26(4):11—25.
