基于SFS 技术的全极化SAR 图像海浪反演机制
2015-05-27赵尚卓于文金
谢 涛,方 贺,陈 伟,赵尚卓,于文金
(1.南京信息工程大学 海洋科学学院,江苏 南京210044;2.武汉理工大学 自动化学院,湖北 武汉430070)
海浪参数反演技术是海洋环境监测与海洋气象预报数据同化的核心,也是当今海洋遥感监测的重点。海洋界主要通过现场测量和遥感测量获取海浪参数。其中现场测量只能获取少量点的海浪参数,对于浩瀚的大洋,只有通过机载和卫星遥感观测才能满足人类对大洋海浪的监测与预报的需求。目前最为实用且较成熟的技术是利用合成孔径雷达(synthetic aperture radar,SAR)进行遥感反演海浪参数[1-7]。
SAR 图像反演海浪参数方法可分为两大类,一类是利用单极化SAR 图像,结合先验信息或猜测谱进行海浪谱反演和参数提取[8-12]。Max -Planck Institut für Meteorologie (MPIM)算法是早期发展的一种基于非线性积分变换的海浪谱反演方法,该方法依赖于由海浪模式模拟的结果输入第一猜测海浪谱。后来,有人利用欧洲遥感(ERS)卫星散射计测量风浪谱,发展成一种半参数化海浪谱反演算法(SPRA),摆脱了对第一猜测谱的限制[13]。因此,在利用SAR 图像反演海浪谱和参数提取方法研究时,注重考虑避免使用第一猜测谱作为输入。另一类是利用全极化SAR 图像的复散射系数,结合其他调制传递函数(MTF)进行海浪谱反演与参数提取[14-15]。全极化SAR 图像反演的优点是所需外部信息相对较少,仅在提取海浪传播方向消除180°模糊时需要外部信息。但目前利用全极化SAR 进行海浪谱反演和参数提取的方法存在依赖于调制传递函数的严重缺陷,从而反演精度取决于调整传递函数描述海面SAR 成像机制的准确性。笔者在既不依赖于第一猜测谱,又不使用调制传递函数的前提下,探索利用全极化SAR 图像反演海浪谱的方法。
1 基于SFS 技术的全极化SAR 图像陆地表面斜率反演
图1 所示为入射电磁波照射成像表面任一像元成像几何示意图。像元在(x,z)平面和(y,z)平面尺寸分别为La和Lr,方位向和距离向分辨率分别为Ra和Rr,tan γ 和tan β 分别为像元在方位向和距离向的斜率,电磁波入射角为θ。
根据图1,可以有如下关系成立:
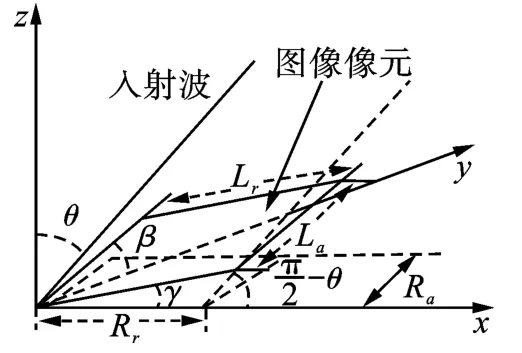
图1 入射波照射像元几何示意图
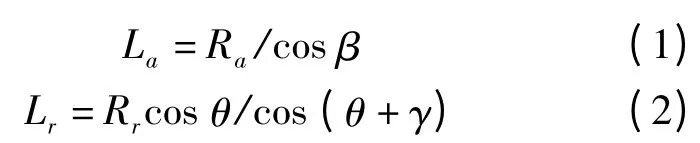
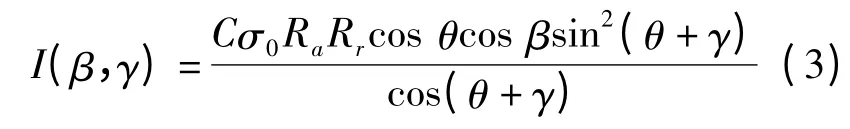
其中,当β =γ =0 时,子图像统计平均后向散射强度I0=Ir(0,0)=Cσ0RaRrsin2θ,σ0为成像区域归一化后向散射系数。不难发现,每个像元与平均后向散射强度的比值R(β,γ)仅与θ,β 和γ 相关,即:
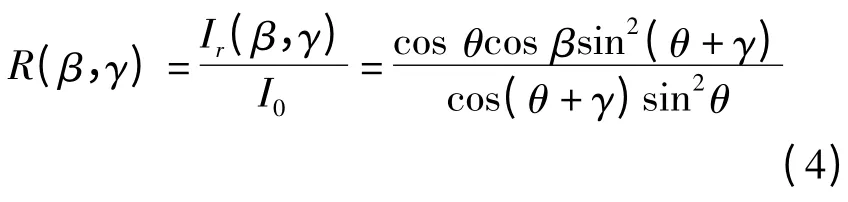
对于SAR 图像,每个像元的电磁波入射角是确定的,如果能确定一个仅与θ,β,γ 相关的独立于式(4)的方程,则可解出β,γ,得到成像区域的斜率分布,从而可反演海浪谱并进行参数提取。
LEE 等[16]发展了陆地成像时,地面斜率(tan β和tan γ)变化引起的极化方位角漂移φ 与电磁波入射角θ 的关系为:
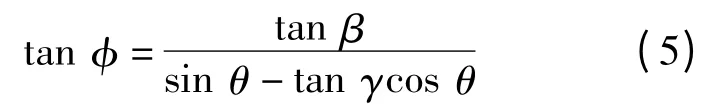
其中,当φ≤π/4 时,φ= φ;当φ >π/4 时,φ=φ-π/2,且有:
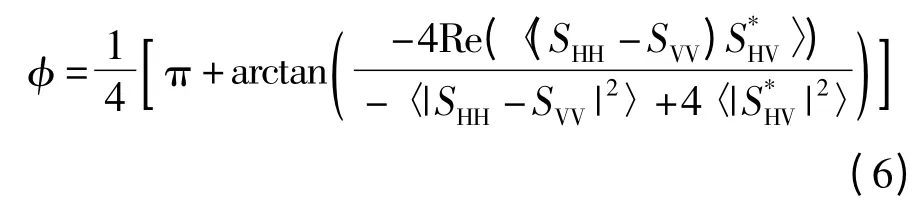
式中:SHH为雷达水平发射水平接收时后向散射系数;SVV为雷达垂直发射垂直接收时后向散射系数;SHV为雷达水平发射垂直接收时后向散射系数;SVH为雷达垂直发射水平接收时后向散射系数;* 为共轭算子。根据互易关系[17],则有SHV=(SHV+SVH)/2。
目前,式(4)~式(6)已被应用于陆地地形的数字高程反演技术,取得较理想的效果[18-19]。
2 全极化SAR 图像海浪反演机理
相对陆地SAR 成像而言,海面SAR 成像机制更为复杂,要将SFS 应用于海浪反演,应该从SAR 成像机制入手,研究基于阴影恢复形状技术的SAR 图像海浪反演机理,并验证该方法海面地形反演的可适用性。
在J监测点使用水平仪进行观测,选取距离基坑较远的一点(30 m以外)为参照点,将参照点与标点上标尺的差值作为对应的相对高程(图2)。
海面SAR 成像主要有3 种机制:①倾斜调制,由散射面的“倾斜”引起局部入射角变化,从而导致后向散射强度的改变;②流体动力学调制,由于长波对短波调制引起Bragg 波谱变化,导致雷达回波强度改变;③速度聚束调制,轨道运动引起的海浪SAR 图像上的周期性图像强度变化。分别采用倾斜调制传递函数(其中,“+”表示VV 极化,“-”表示HH 极化)、流体动力学调制传递函数Rhydro=4.5和速度聚束调制传递函数来描述上述3 种成像机制。其中,ka、kr分别为方位向和距离向海浪波数分量;R为SAR 平台与散射小面的距离;V为平台的地面轨迹速度为海浪角频率;g为重力加速度;ψ 为方位角即海浪传播方向与平台运行轨迹方向的夹角,满足sinψ=kr/k。
2.1 倾斜调制机制
如果海面是静态的,则SAR 海面成像主要由倾斜调制引起,式(4)~式(6)完全可以直接应用于海浪谱反演。因此源于陆地地形反演应用的SFS 技术的主要机制为倾斜调制机制,而该机制也是海面SAR 成像过程中的主要机制,其主要作用是由于散射面的倾斜致使雷达后向散射截面的变化,式(3)为该机制的数学表达式。
如果海面是动态的,则长短波之间存在水动力学调制作用,另外海水运动导致速度聚束调制SAR 成像,这两个机制是海面成像所特有的机制。如果将SFS 技术应用于海浪谱反演,必须考虑这两个机制带来的影响。即如果式(4)~式(6)隐含了某个机制或者该机制在整个SAR 成像过程中所占比例可以忽略,则可认为该机制是基于SFS 技术的全极化SAR 海浪谱反演的主要机制之一或者说是可以被忽略的机制。
2.2 速度聚束调制机制
笔者研究速度聚束调制对基于SFS 技术的全极化SAR 海浪谱反演的影响。实际上式(4)~式(6)隐含了速度聚束调制机制。根据ALPERS等[20]的研究,当散射小面方位向分辨率ρ'a(x0),及平均雷达截面σ(x0)仅为方位向坐标x0的函数时,图像强度为:


其中,C(x0)=对于静态海面,根据实孔径雷达极化后向散射系数可计算x0处的方位角为:
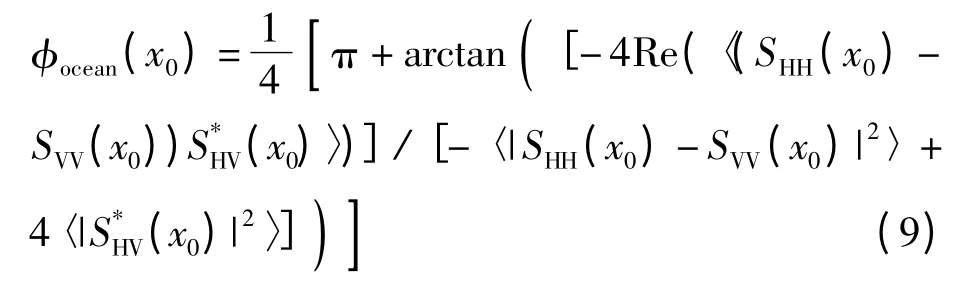
而对于动态海面,由SAR 极化后向散射系数可计算SAR 图像x处的方位角为:
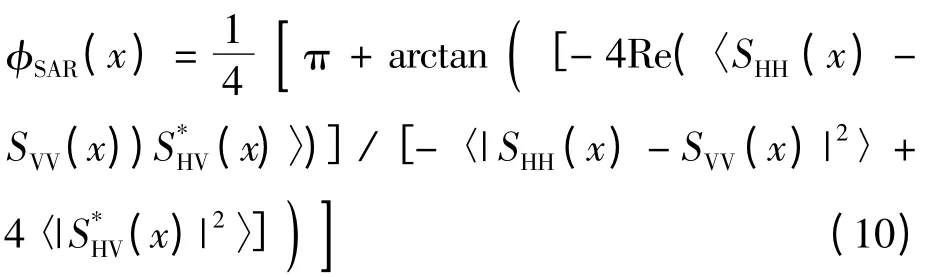
将式(8)代入式(10)则有:
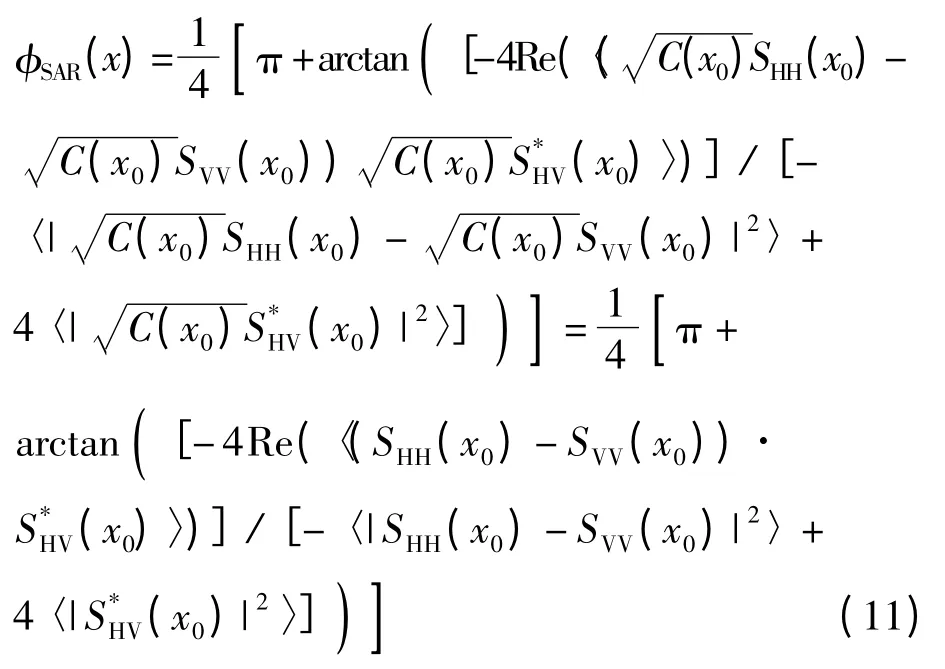
即有φSAR(x)= φocean(x0)。由式(8)和式(11)可以看出,由于速度聚束调制函数系数C(x0)与雷达极化方式无关,即每种极化方式的速度聚束函数系数相同,因此在利用全极化散射系数计算方位角时,速度聚束调制被隐含了。
因此,除了倾斜调制机制以外,由于采用全极化SAR 图像,基于SFS 技术的全极化SAR 海浪谱反演机制也隐含了速度聚束机制。
2.3 流体动力学调制
流体动力学调制是SAR 成像的另一非线性调制机制,需要讨论其对SAR 海浪反演的影响。SAR 图像强度PI(k)与海浪高度谱Pξ(k)之间的线性调制函数为:
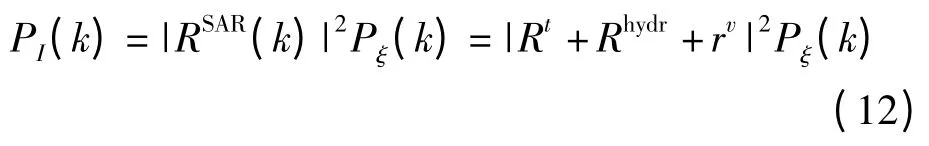
考虑流体动力学调制机制的贡献,需估计流体动力学调制在所有调制传递函数中所占比例rhydr。由式(12)及上述各调制传递函数表达式可知:

根据式(13)可以估计流体动力学调制的贡献,图2 所示为流体动力学调制在所有调制传递函数中所占比例rhydr随雷达入射角θ 和方位角ψ的变化,其中图2(a)为HH 极化方式SAR 成像过程中,流体动力学调制在所有调制传递函数中所占比例rhydr,图2(b)为VV 极化方式SAR 成像中流体动力学调制机制的贡献。

图2 流体动力学调制在所有调制传递函数中所占比例
数值结果表明,除了海浪沿与距离向夹角很小范围内的方位角情形(ψ=90°左右)外,流体动力学调制对海面SAR 成像的影响可以忽略。如图2(a)所示,HH极化收发方式SAR海面成像时,所有入射角范围内,当方位角ψ≤44°时,流体动力学调制在所有调制传递函数中所占比例rhydr≤1/1 000;当44°<ψ≤67°时,rhydr≤1/100;当67°<ψ≤81°时,rhydr≤1/20;当81°<ψ≤84°时,rhydr≤1/10;当ψ >84°时,rhydr>1/10。即考虑所有入射角适用情形,当方位角ψ≤84°时,不考虑流体动力学调制影响时,所采用SFS 技术的全极化SAR 海浪谱反演方法的误差很小。VV 极化收发方式SAR 海面成像如图2 (b)所示,存在类似情形,即当方位角ψ≤34°时,流体动力学调制在所有调制传递函数中所占比例rhydr≤1/1 000;当34°<ψ≤65°时,rhydr≤1/100;当65°<ψ≤80°时,rhydy≤1/20;当80°<ψ≤84°时,rhydr≤1/10,当ψ >84°时,rhydr>1/10。比较HH 极化和VV 极化两种情形,流体动力学调制对海面SAR 成像的影响可以忽略的临界值为方位角ψ =84°。也就是说当方位角84° <ψ≤90°时,SFS 技术的全极化SAR海浪谱反演方法误差较大。因此,可以总结出SFS 技术的全极化SAR 海浪谱反演方法适用范围为ψ≤84°(当rhydr≤1/10 时,流体动力学调制对海面SAR 成像的影响可以忽略)。
另外,笔者还计算了图2 中流体动力学调制在所有调制传递函数中所占比例的平均值其中,图2(a)所示HH 极化方式SAR 成像的0.017 3,而图2(b)VV 极化方式SAR 成像的0.030 4。因此平均而言,在利用SFS 技术进行全极化SAR 图像海浪谱反演时,式(4)计算Ir(β,γ)/I0时,采用HH 极化图像强度要比采用VV 极化图像强度所得结果精度高得多,特别是在方位角ψ值较大时,相对于VV 极化SAR 图像而言,采用HH 极化SAR 图像优势更为明显。
针对上述3 种海面SAR 成像机制,分析和证明了利用SFS 技术进行全极化SAR 图像海浪谱反演和参数提取的可行性和适用范围。从机理上来说,该方法的主要误差来源于忽略流体动力学调制对海面SAR 成像的影响,通过理论推导和数值模拟发现,在绝大多数情形,该误差很小,可以忽略。
3 结论
基于发展新的海浪谱反演方法的目的,笔者试图将SFS 技术应用于发展SAR 图像海浪谱反演技术,提出了利用SFS 技术和全极化SAR 图像进行海浪谱反演的新方法,并从SAR 成像的倾斜机制、速度聚束机制和流体动力学机制3 个方面对所提出的新方法反演海浪谱的可行性进行论证,发现除了SFS 包含倾斜调制机制外,利用全极化SAR 图像计算方位角漂移时,实际上隐含了速度聚束调制,这是因为每种极化方式都包含了相同的调制传递函数系数,计算公式中分子分母的调制传递函数系数可以约分掉。另外,流体动力学调制机制是笔者提出新方法所不能包含的一种机制,但通过理论分析和数值模拟计算发现,除了方位角处于90°附近很窄的范围内的情形,流体动力学调制机制的影响可以忽略。
[1]刘丽娜,陈曦,赵现斌,等.机载SAR 探测海面风场、海浪和海洋内波方面的分析与研究[J]. 气象水文海洋仪器,2012,2(2):6 -10.
[2]范林刚,陈泽宗,金燕,等.微波多普勒雷达海浪参数提取算法[J].华中科技大学学报:自然科学版,2012,40(10):21 -24.
[3]刘文俊,孔毅,赵现斌,等. 基于交叉谱法的C 波段机载SAR 海浪反演[J]. 解放军理工大学学报:自然科学版,2014,15(4):380 -385.
[4]肖鹏,种劲松.基于拟线性变换的海浪方向谱反演方法研究[J].科学技术与工程,2011,17(11):3899-3902.
[5]史伟哲. 星载SAR 海洋场景仿真与反演方法综述[J].航天器工程,2011,20(1):50 -56.
[6]ROMEISER R,GRABER H C.A new approach of ocean wave parameter estimates from C-band scan SAR images[J]. IEEE Transactions on Geoseience and Remote Sensing,2015,53(3):1320-1344.
[7]CHEN Z B,HE Y J.A new algorithm to retrieve wave parameters from marine X-band radar image sequences[J].IEEE Transactions on Geoseience and Remote Sensing,2014,52(7):4083-4091.
[8]LAI D Y,DELISI D P. Spatial distribution of surface wave field in coastal regions using spaceborne synthetic aperture radar images[J].International Journal of Remote Sensing,2010(31):4915 -4931.
[9]HASSELMANN K,HASSELMANN S.On the nonlinear mapping of an ocean wave spectrum into a synthetic aperture radar image spectrum and its inversion[J].Journal of Geophysical Research,1991(96):713-729.
[10]HASSELMANN S,BRUNING C,HASSELMANN K,et al.An improved algorithm for the retrieval of ocean wave spectra from synthetic aperture radar image spectrum[J].Journal of Geophysical Research,1996(101):615 -629.
[11]SCHULZ S J,LEHNER S,HOJA D. A parametric scheme for the retrieval of two - dimensional ocean wave spectra from synthetic aperture radar look cross spectra[J]. Journal of Geophysical Research,2005(110):5004 -5017.
[12]LEHNER S,PLESKACHEVSKY A,BRUCK M.High- resolution satellite measurements of coastal wind field and sea state[J]. International Journal of Remote Sensing,2012,33(23):7337 -7360.
[13]MASTENBROEK C,DEVALK C F.A semiparametric algorithm to retrieve ocean wave spectra from synthetic aperture radar[J]. Journal of Geophysical Research,2000(105):3497 -3516.
[14]ZHANG B,PERRIE W,HE Y.Validation of RADARSAT-2 fully poarimetric SAR measurements of ocean surface waves[J].Journal of Geophysical Research,2010(115):6031 -6043.
[15]HE Y,SHEN H,PERRIE W. Remote sensing of ocean waves by polarimetric SAR[J]. Journal of Atmospheric and Oceanic Technology,2006(23):1768-1773.
[16]LEE J S,JASEN R W,SCHULER D L. Polarimetric analysis and modeling of multi frequency SAR signatures from Gulf Stream fronts[J]. IEEE Journal of Ocean Engineering,1998,23(4):322 -333.
[17]SEVGI L.Reciprocity:some remarks from a field point of view[J]. Antennas and Propagation Magazine,IEEE,2010,52(2):205 -210.
[18]CHEN X,WANG C,ZHANG H.DEM generation combining SAR polarimetry and shape -from -shading techniques [J]. IEEE Geoscience and Remote Sensing Letters,2009,6(1):28 -32.
[19]CHEN Z,QIN Q,LIN L,et al. DEM densification using perspective shape from shading through multispectral imagery[J]. IEEE Geoscience and Remote Sensing Letters,2013,10(1):145 -149.
[20]ALPERS W R,ROSS D B,RUFENACH C L.On the detectability of ocean surface waves by real and synthetic aperture radar[J]. Journal of Geophysical Research,1981(86):6481 -6490.
