基于SD 的工程合谋防治演化博弈动态分析
2015-05-26周洪涛
俞 乐,周洪涛,曾 伟
(华中科技大学 自动化学院,湖北 武汉430074)
作为经济社会的一个顽疾,合谋存在于人类社会发展的各个阶段、各个领域[1]。针对建设领域合谋腐败现象,学者多采取经济学领域委托代理模型与博弈模型相结合的研究模式。LAFFONT 运用博弈模型和不完全契约分析了组织行为,建立了监管人、委托人和代理人三方博弈模型[2]。余晓钟等建立了业主、承包商和监理方三方合谋静态博弈模型,在模型分析的基础上提出了加大监督力度、合谋惩罚力度、完善信用体系和降低信息不对称等防治合谋的方法[3]。陈赘等建立了博弈的不完全信息动态博弈模型,得出了合谋条件及防范机制[4]。KREPS 在重复博弈分析下得出多次重复博弈更有可能出现群体合谋腐败的结论。乌云娜等针对合谋人并非完全理性,提出用前景理论刻画合谋人在合谋过程中的不同风险态度,更准确地解释了合谋人对不确定的收益和损失所产生的不同心理效应[5]。上述研究多为一次性博弈,而建设项目施工周期长,行为人有可能在不同的子项目中多次相遇,即存在多次博弈。并且当前研究多利用演化博弈理论刻画工程招投标中围标行为的防范[6],工程质量合谋行为防范研究鲜有所见。因此,笔者将前景理论与演化博弈相结合,改善原有的博弈模型假设,并对博弈模型进行系统动力学仿真验证。通过仿真分析可行的防合谋机制,使政府工程项目监管博弈模型更具实际运用价值。
1 合谋演化博弈分析
1.1 模型假设
假设1 博弈中只存在3 类群体:政府项目投资人、监理方和承包商,后两者组成合谋体。政府行动集是{打击合谋,不打击合谋}。监理方和承包商的行动集均为{合谋,不合谋},监理方合谋是为了自身利益向承包商寻租,有意疏于对承包商施工行为的监管;承包商合谋是为了追求最大的经济利益,通过向监理方行贿达到隐藏自身努力程度的目的。
假设2 博弈群体中个体均为有限理性的行为人,做决策时基于自身对策略价值的感知而非实际效用情况,且这种感知价值的特征符合累计前景理论,即具有收益满足V=Σiπ(pi)v(Δwi),其中,pi为事件i发生的客观概率;Δwi为事件i发生后参与者所得的实际收益与参照点的差[7];v(Δwi)为参与者对于Δwi的主观价值函数;决策权重π(pi)为参与者的主观概率,其是客观概率的函数。行为人对既定的收入或损失(不存在风险)不存在心理效应的偏差,不用v(x)收益函数表示;而行为人对于合谋所导致的收入或损失的不确定性才存在心理效应v(x)(如合谋时的额外收益、意外惩罚或未知的奖励)。
政府和监理方博弈是不完全信息模型。假设只有监管且打击成功与否对于合谋方有心理效用,政府打击成功的概率为α。合谋方对政府打击力度抱有侥幸心理,是前景理论主观概率形成的原因,合谋方主观认为打击成功的概率为π(α)。
假设3 模型参数假设。政府实行代建制项目的社会收益为Vg,对项目监管查处成本为Cg,政府对监理和承包商的监管强度即惩罚系数分别为Ks和Kc。监理方合法收入为Vs,从承包商抽得的不法额外收益为Rc,合谋被打击后的惩罚为KsRc。承包商的合法收入为Vs,因合谋压缩的额外收益为RTc,合谋被打击后的惩罚为KcRTc。Hs表示因项目提前竣工或节余资金等国家给予监理方的奖励。Fs表示合谋发生并被成功查处后监理方遭受的名誉损失。引入质量安全风险成本,监理方与承包商的安全风险成本线性相关,即若承包商承担的安全风险成本为L,则监理方承担的安全风险成本为kL,k为风险传递系数。
1.2 演化博弈模型分析求解
根据模型假设及相关博弈分析理论,假设政府是否监管不再对合谋双方有心理效用,只有打击成功与否对合谋方有心理效用,政府选择打击合谋的比例为y,选择不打击合谋的比例为1 -y;监理方选择与承包商合谋的比例为x,选择不合谋的比例为1 -x。政府与监理方博弈收益矩阵如表1 所示。

表1 政府、监理博弈收益矩阵
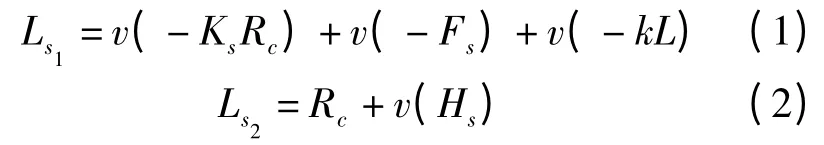
政府打击合谋失败的损失为:

政府打击合谋成功的收入为:)
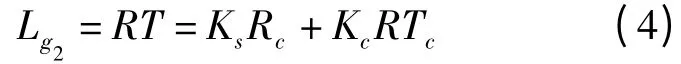
由表1 可知,监理选择与承包商合谋的期望收益Us1,选择不合谋的期望收益Us2,平均收益Us,复制动态方程F(x)分别为:
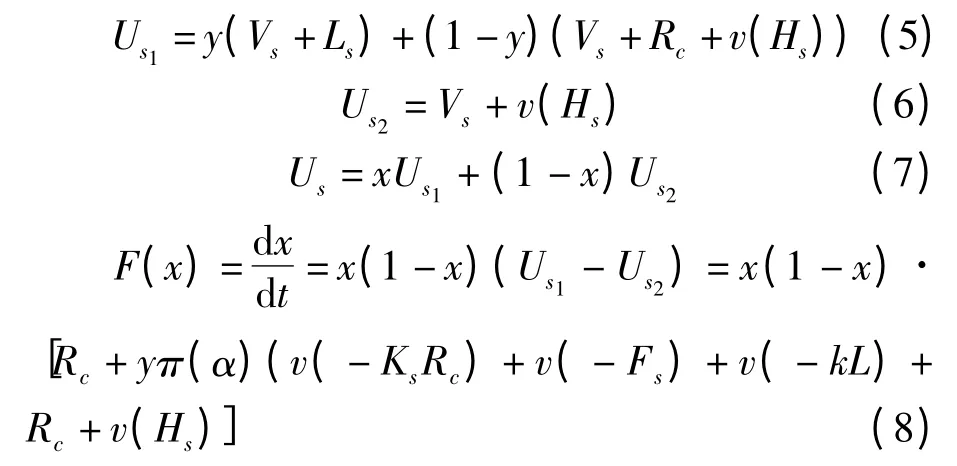
同理,政府选择打击合谋的收益Ug1,选择不打击合谋的收益Ug2,平均收益Ug,复制动态方程F(y)分别为:
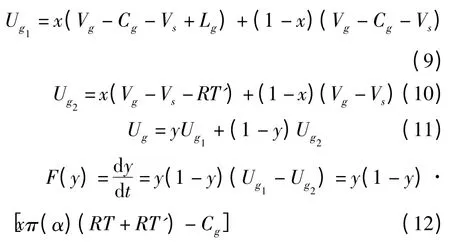
令(F(x),F(y))= (0,0),得到该复制动态系统有5 个均衡点,分别为:E1(0,0),E2(0,1),E3(1,0),E4(1,1),E5(x*,y*)(E5(Cg/π(α)vg,-Rc/π(α)vs),其中vs=v(-KsRc)+v(-Fs)+v(-kL)-Rc-v(Hs),vg=RT+RT')。但这些系统均衡点不一定满足演化博弈稳定策略,需根据每个均衡状态的具体情况加以判断[8]。笔者根据FRIEDMAN 提出的方法[9],一个由微分方程描述的群体动态均衡点的稳定性可由该系统的雅克比矩阵的局部稳定性分析得到。因此,分别对式(8)和式(12)求x、y的偏导数,可得雅克比矩阵:
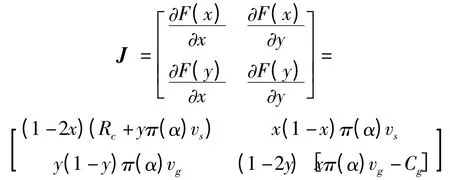
矩阵的行列式detj和迹trj分别为:
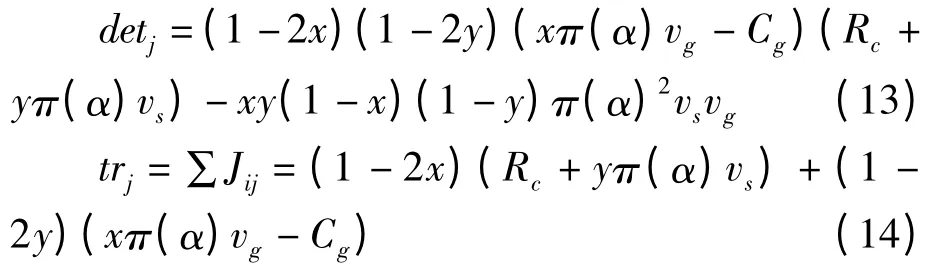
演化稳定策略(ESS)的判定,可以用均衡点的雅克比矩阵的行列式detj及trj的符号判断。对于离散系统,当且仅当detj>0 且trj<0 时,该均衡点是稳定的。因此上述5 个平衡点的稳定性受π(α)vg-Cg和Rc+π(α)vs大小的影响,分别计算各点的detj及trj,共4 种情况:
(1)π(α)vg-Cg>0 且Rc+π(α)vs>0 时,E1、E3是鞍点,E2不稳定,E4是ESS;
(2)π(α)vg-Cg>0 且Rc+π(α)vs<0 时,E1、E2、E3、E4均是鞍点,E5是中心点,没有ESS;
(3)π(α)vg-Cg<0 且Rc+π(α)vs>0 时,E1、E4是鞍点,E2不稳定,E3是ESS;
(4)π(α)vg-Cg<0 且Rc+π(α)vs<0 时,E1、E2是鞍点,E4不稳定,E3是ESS。
综上所述,演化博弈的每一个平衡点都不是满足一般情况的ESS。但是,在某些特定状况下存在ESS:①当π(α)vg-Cg<0,即π(α)<Cg/vg时,E3是ESS;②当π(α)vg-Cg>0 且Rc+π(α)·vs>0,即Cg/vg<π(α)<-Rc/vs时,E4是ESS。
2 演化博弈SD 仿真及策略分析
2.1 SD 演化模型建立
用VesimPLE6.3 建立工程防合谋演化博弈SD 模型,主要由4 个流位、2 个流率、22 个中间变量,以及11 个外部变量组成,如图1 所示。
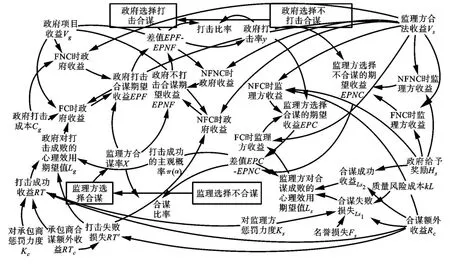
图1 工程防合谋演化博弈SD 模型
假设起始时间为0,终止时间为5 000,时间间隔为0.25,以某代建项目为例,政府收益Vg=10,政府打击合谋成本Cg= 0.5,监理方代建费为总效益的2%,节余奖励为节余金额的30%。则监理方合法收益Vs=2,监理方合谋额外收益Rc= 0.5,承包商合谋额外收益RTc= 0.2,奖励Hs= 0.06。笔者设定对监理方的惩罚系数Ks和对承包商的惩罚系数Kc都为3,合谋名誉损失Fs=4,监理方质量安全成本kL=0.05。
依据以上外部变量取值,vs= -10.37,vg=2.8,E5(0.17/π(α),0.05/π(α)),取边际递减敏感性程度系数α 为0.88,厌恶损失效应程度λ为2,v(x)测算公式为[10]:
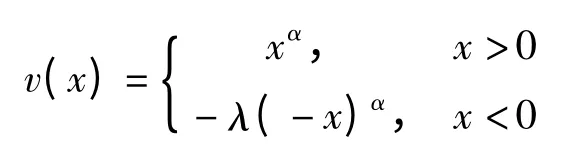
2.2 仿真策略分析
2.2.1 π(α)<Cg/vg时演化过程仿真
(1)博弈双方初始战略均采用Nash 均衡纯策略。取π(α)<Cg/vg=0.1,博弈双方初始均采用Nash 均衡E1(0,0),E2(0,1),E3(1,0),E4(1,1),输入纯战略Nash 作为初始值进行模拟,双方演化过程如图2 和图3 所示。

图2 监理初始值为均衡状态
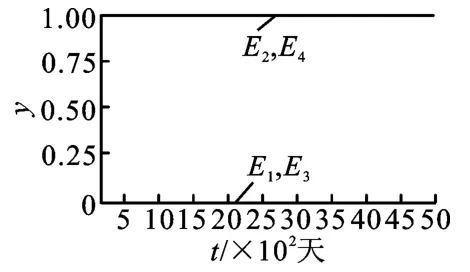
图3 政府初始值为均衡状态
对于E1和E4,当监理方总是不选择与承包商合谋时,政府业主方的最佳决策是不监管打击;当监理方总是选择与承包商合谋时,政府业主方的最佳决策是采取监管进行打击。但是对于E2和E3却是监理方选择不合谋,政府反而总采取打击措施;而监理方与承包商合谋时,政府反而不进行监管打击,导致自身利益受损。E2和E3可以理解为没有任何个体采用新的不同策略,即没有新策略供个体进行学习改进,因此也能处于一定的稳定状态。
进一步分析可知,E1有微小突变(0.2,0),会迅速演变到E3状态达到稳定;E2突变(0.2,1),系统将迅速稳定到E4状态;E4突变(1,0.99),也将迅速演化到E3状态稳定下来;E3突变(1,0.1)仍能演化到E3(1,0)稳定下来。E4和E3突变演化图如图4 和图5 所示。
(2)博弈双方初始战略均采用混合策略。当博弈双方采取混合战略如x=0.2,y=0.4 时,也会迅速演化到E3(1,0)状态,即监理方选择合谋,而政府却不打击。演化过程如图6 所示。
由上述分析可知,在行为人对不确定得失的主观概率π(α)<Cg/vg时,E3(1,0)状态是演化稳定策略,这种稳定状态很难被打破。即当监理方主观判断政府打击成功概率小于一定值时,监理方会选择合谋,政府也会渐渐因利益原因选择不打击合谋,该情况不利于政府项目的质量安全。
2.2.2Cg/vg<π(α)<Rc/vs时演化过程仿真
为满足Cg/vg<π(α)<Rc/vs,需重新取值,令Vg=3,Cg=0.01,Vs=0.6,Rc=0.4,RTc=0.2,Hs=0.045,Ks=Kc=2,Fs=1,kL=0.03。此时Cg/vg=0.05,-Rc/vs=0.1,取π(α)=0.07。
(1)博弈双方初始战略均采用Nash 均衡纯策略。在Cg/vg<π(α)<-Rc/vs的情况下,对各个稳定状态的演化过程和发生微小突变的演化过程图进行对比,发现E1在微小突变(0.1,0)下,会稳定到E3(1,0)状态;E2突变(0.1,1)会稳定到E4(1,1)状态;E3突变(1,0.1)也会稳定到E4(1,1)状态;E4(1,0.9)突变稳定到E4(1,1)。E2和E4的突变演化过程图如图7 和图8 所示。
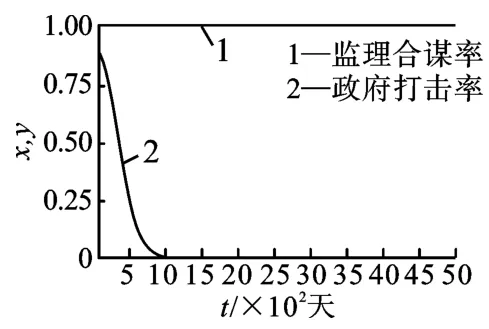
图4 E4 状态在x=1,y=0.99 的突变
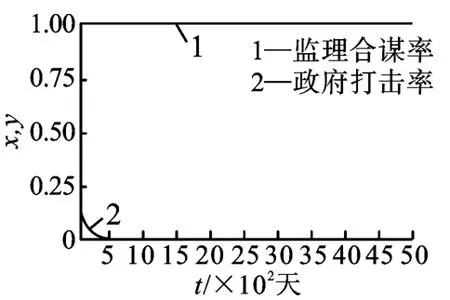
图5 E3 状态在x=1,y=0.1 的突变
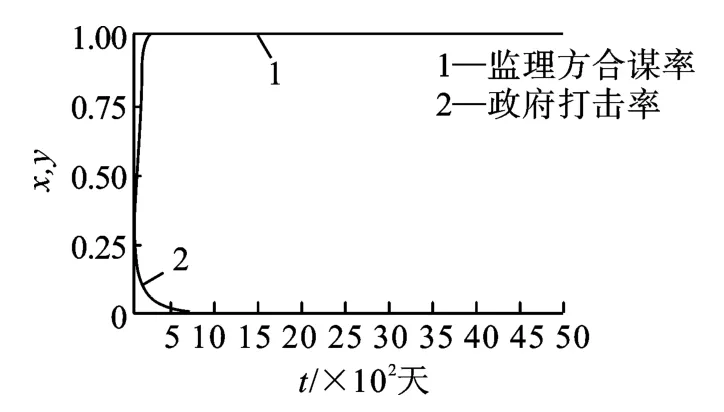
图6 初始状态混合战略x=0.2,y=0.4 的突变
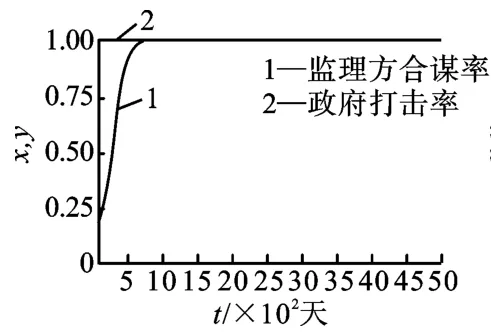
图7 初始E2(0.1,1)突变到E4(1,1)
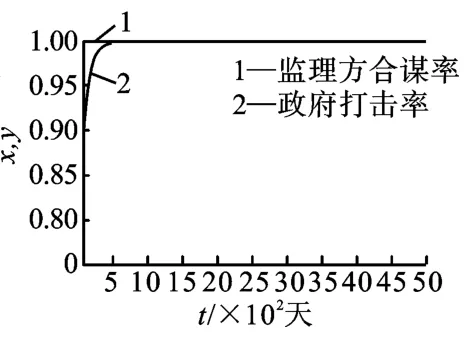
图8 初始E4(1,0.9)突变到E4(1,1)
(2)一般情况初始值。博弈双方初始时采取x=0.2,y=0.4 的一般战略,演化过程如图9 所示。混合战略(0.2,0.4)会迅速演变到E4(1,1)状态。
这证明了行为人不确定得失的主观概率Cg/vg<π(α)<-Rc/vs时,E4(1,1)状态是演化稳定策略,该稳定状态很难被打破。即当监理方主观判断政府打击合谋成功的概率在一定范围时,监理方会选择合谋,政府也会选择打击合谋。
但是从数据选取和π(α)的取值范围可知,这种情况是较难出现的,政府对于高风险追求的监理方,为避免出现(合谋,不打击)不利状况,必须采取打击策略,使演化能稳定到(合谋,打击)的状态。
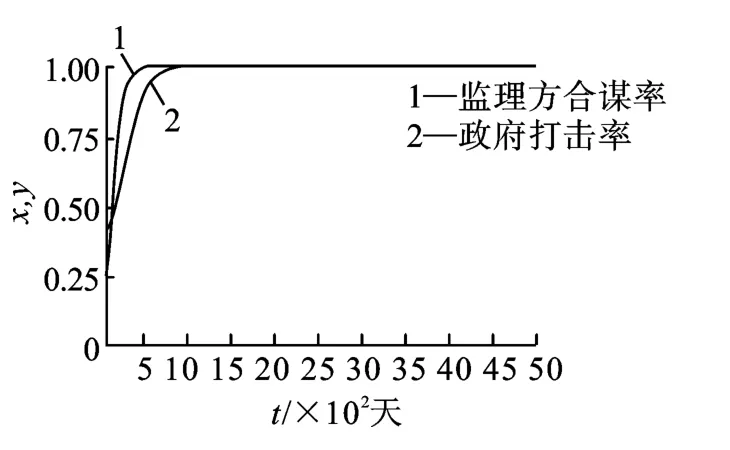
图9 初始状态混合策略(0.2,0.4)稳定到E4(1,1)
2.2.3 π(α)vg-Cg>0 且Rc+π(α)vs<0 时演化过程仿真
(1)混合战略Nash 演化仿真。用第一组数据,取π(α)>Cg/vg=0.3,在该情况下有E5(0.6,0.15)。仿真结果证明E1、E2、E3、E4都不是稳定状态,微小突变会使它们互相演变。E5的演化过程如图10 所示,在2π(α)vg-Cg>0 且Rc+π(α)vs<0 时,E5是中心点,此时不存在稳定点。
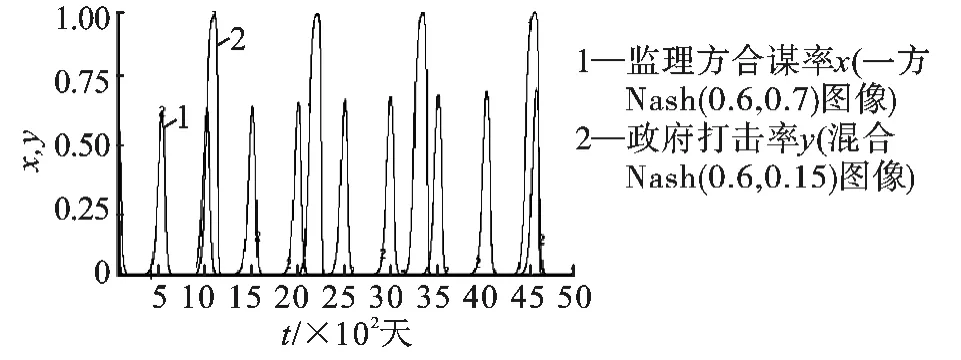
图10 初始状态E5(0.6,0.15)和混合状态(0.6,0.7)对比
由图10 可知,当博弈一方选择混合战略Nash 均衡,另一方随机选择,随着时间和博弈次数的增加,双方策略的变更波动大且极不易控制。
(2)动态惩罚机制的改良演化。针对没有稳定点并且波动难以控制的状况,笔者引进动态惩罚机制进行改良。合谋比例x表示合谋导致的工程安全风险严重程度,则安全风险严重程度越高,政府打击成功后的惩罚力度成比例增加。加入动态惩罚Ks=Kc=3x后的演化过程如图11 所示。由图11 可知,一定程度上的加大惩罚力度基数或减小打击成本能有效降低监理方合谋率。

图11 动态惩罚改良后的演化过程
3 对策建议
(1)差异化监管威慑机制。政府要实时了解监理行业现状,监理方风险态度,对监理方进行分类,有针对性地进行监管。对于π(α)较低的监理方,为避免出现(合谋,不打击)的演化稳定结果,在π(α)<Cg/vg时,政府应加大监管和打击力度;对于π(α)较高的监理方,可在一定程度上压缩监管成本,使其能出现3π(α)vg-Cg>0 且Rc+π(α)vs<0 时较稳定且合谋概率较低的状态,压缩的成本还可用于监管π(α)较低的监理方。
(2)科学的惩罚机制。科学的惩罚机制能在合理的范围内加大惩罚力度(倍数)来抑制合谋的同时,也能避免长期演化的波动性。从合谋防治长效机制角度来看,有效结合动态惩罚政策,即惩罚力度随合谋导致的工程安全风险程度不同而变化,有利于达到稳定控制合谋的目的。
(3)监管成本控制。通过施工现场监控、人员定位等手段使施工现场透明化,监理方和承包商的行为均在一定监控范围内,承包商隐瞒努力程度的信息不对称无法形成,合谋便无法达到。另外组织监理方、承包商参观政府监控安全中心,宣传合谋惩罚条例和处罚实例,让合谋方体验到政府的打击能力和惩罚的严厉性,有助于提高监理方π(α),且达到威慑作用。
(4)健全行业名誉体系,加强社会监督。政府应积极依法制定监理行业信誉评价体系,客观评价监理行业水准。良好的信誉体系能让政府清晰地了解监理行业现状,将信誉较低甚至合谋多次的监理方纳入行业黑名单,无论私有或是政府项目都不与其签订代理合约,这种信誉低的监理方也必将被行业淘汰。
[1] 罗建兵.合谋的生成与制衡:理论分析与来自东亚的数据[D].上海:复旦大学图书馆,2006.
[2] 乐云,单明. 建设工程领域工程合谋现象研究综述[J].工业技术经济,2013,1(1):145 -151.
[3] 余晓钟,张焕杰.政府工程项目业主、承包商和监理方的合谋博弈分析[J]. 经济问题探索,2008(11):86 -92.
[4] 陈赘,刘肇城. 公共工程项目主体合谋条件的动态博弈分析[J].公路与汽车,2006(6):104 -105.
[5] 乌云娜,杨益晟,冯天天,等.基于前景理论的政府投资代建项目合谋监管威慑模型研究[J]. 管理工程学报,2013,1(2):168 -176.
[6] 范如国,李丹.基于演化博弈的工程投标中的围标行为及对策分析[J].价值工程,2011,30(1):64-66.
[7] 周国华,张羽,李延华,等.基于前景理论的施工安全管理行为演化博弈[J]. 系统管理学报,2012,7(4):501 -508.
[8] 易余胤,盛昭瀚,肖条军.合作研发中机会主义行为的演化博弈分析[J].管理科学学报,2005,8(4):80-87.
[9] FRIEDMAN D.On economic applications of evolutionary game theory[J].Journal of Evolutionary Economics,1998(8):15 -43.
[10] 贾璐. 基于SD 工程建设安全监管烟花博弈研究[J].南昌大学学报:工科版,2012,3(1):42 -48.
