基于模糊自适应PID的SR电机DITC系统仿真研究

康荣波 杨明发

（福州大学电气工程与自动化学院，福州 350116）

开关磁阻电机（Switched Reluctance Motor，SRM）具有简单坚固、体积小、重量轻、工作可靠、制造成本低廉等诸多优良特性，形成了与其他类型电动机竞争的潜在优势[1]。但是由于SRM 的双凸极结构和很强的磁场非线性使噪声和转矩脉动问题较其他传统电机更加严重[2]。采用常规的控制方法如电流斩波控制、电压PWM 控制和角度位置控制方法造成转矩脉动较大，难以满足SRM 非线性、变结构、变参数的要求。

研究者在减小转矩脉动、提高系统性能方面做了大量深入的研究[1-3]。目前已有的针对转矩脉动的改进型控制策略包括直接转矩控制、变结构控制、模糊控制等。文献[3]把转矩分配函数与模糊神经网络转矩逆模型结合，实现了转矩脉动抑制。文献[4]用转矩、磁链双闭环的直接转矩控制方法达到抑制转矩脉动目的；文献[5]提出了基于RBF 神经网络的单神经元PID 控制方法，改善了电机调速性能。文献[6]把直接转矩控制与模糊PI 调速系统结合起来，在抑制转矩的基础上改善了调速性能。本文提出了把开关磁阻电机直接瞬时转矩控制（DITC）策略与模糊自适应PID 控制器相结合的新方法，其中DITC控制无需磁链闭环，把任意时刻瞬时转矩作为控制量来确定功率开关管工作状态。仿真表明，该方法不仅能有效抑制转矩脉动，而且能很好的改善调速系统，使其具有系统超调小、转速稳定时间短、鲁棒性强的优点。

1 开关磁阻电机DITC 系统控制方法

开关磁阻电机DITC 系统主要包括转矩估算单元、模糊自适应PID 控制器、DITC 转矩滞环控制器、不对称半桥式功率变换器等。转速外环误差输入模糊PID 控制器，控制器输出的期望转矩再与电机实际转矩形成内环，把转矩误差与各相位置信息输入DITC 转矩滞环控制器，最后输出用以控制功率变换器开关管状态的信息。

1.1 不对称桥式功率变换电路的开关状态

电路根据开关管通断情况分为三种工作状态：两个开关管全部导通时，电机绕组外加正电压，设此时状态为S=1；两个开关管一通一断时，电机绕组外加零电压，设此时状态S=0；两个开关管全部关断时，电机绕组外加负电压，设此时状态S=-1。功率变换电路三种状态如图1所示。

图1 功率变换电路工作状态

1.2 DITC 转矩滞环控制器设计原理

与传统的控制器不同，DITC 认为转矩是直接控制的变量，相电压由转矩命令和瞬时转矩之差决 定[7]。根据任意时刻导通角的重叠情况，可以把电机工作区域分为单相导通区和换相重叠区。如图2所示，其中区域1、3、5、7 为单相导通区，区域2、4、6、8 为换相重叠区。

图2 四相绕组电流-位置角示意图

在单相导通区时，如图3（a）所示，以A 相为例，当瞬时转矩T减小到与给定转矩的偏差值大于ΔTmin时，S 的工作状态从0 变1，给绕组正电压以增大瞬时转矩T；当瞬时转矩T增大到与给定转矩偏差值小于-ΔTmin时，S 的工作状态从1 变成0，让绕组电压降为0 以减小瞬时转矩T。

在换相重叠区时，如图3（b）所示，以A、B换相时为例，此时瞬时转矩为两相转矩之和。假设换相初期A 相的S=0，B 相的S=1。当B 相产生转矩不足时，瞬时转矩下降，直到转矩差大于ΔTmax时让A 相的S 由0 变1 以增大瞬时转矩；当瞬时转矩增至转矩偏差小于0 时再把A 相的S 置0；当瞬时转矩继续增大至转矩偏差小于-ΔTmin时，B 相的S也置0 以进一步抑制瞬时转矩；此后若转矩继续增大至偏差小于-ΔTmax时，把A 相的S 变成-1 以最大限度抑制转矩，直到转矩减小至偏差为0 时再把A的S 转为0；当转矩减小到偏差大于ΔTmin时把B 相重新置1 以增大瞬时转矩。这样，通过DITC 的开关动作，换相区域的瞬时转矩也得到了控制。

图3 DITC 控制方法原理图

2 模糊自适应PID 控制器

模糊自适应PID 控制器将根据误差e和误差变化de来确定PID 参数的经验用模糊规则表示；在实际控制过程中，根据实时误差e和误差变化de来进行模糊推理以确定PID 参数的变化，将参数传给PID控制器[8]。模糊推理器以误差e与误差变化de作为输入，以PID 控制器的三个参数ΔKp、ΔKi、ΔKd作为输出，随时根据控制对象模型变化来在线自适应调节PID 参数。相比于传统PID 控制器，模糊自适应PID 控制器对控制系统调速性能改善具有良好的综合效果。其控制原理图如图4所示。

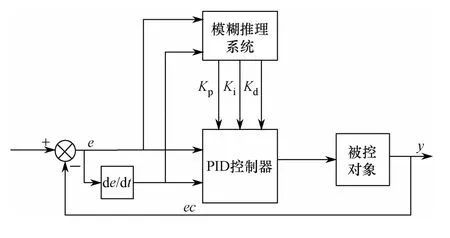
图4 模糊自适应PID 控制系统框图

2.1 模糊化与解模糊处理

模糊控制器是基于模糊控制语言进行描述和推理的，而输入的e和ec是精确值，因此首先应该通过量化因子将e和ec从基本论域映射到模糊论域中，转化成模糊量E和EC。本文的调速目标是要电机转速稳定在 1000r/min，所以取e基本论域为［-1000，1000］，取ec的基本论域为［-220000，220000］；E和EC的模糊论域均取［-6，6］；由此可以确定量化因子Ke=6/1000，Kec=6/220000。模糊变量E和EC都取七个模糊语言值，即“正大”（PL）、“正中”（PM）、“正小”（PS）、“零”（ZO）、“负小”（NS）、“负中”（NM）和“负大”（NL）。为了简化计算，采用了三角形隶属函数，E与EC的隶属函数如图5所示。

图5 E 和EC 的隶属函数

采用加权平均法[9]解模糊得到模糊输出值。设模糊输出值为KP、KI、KD，其模糊语言值也取为“正大”（PL）、“正中”（PM）、“正小”（PS）、“零”（ZO）、“负小”（NS）、“负中”（NM）和“负大”（NL），模糊论域为［-6，6］，隶属函数如图6所示。

图6 KP、KI、KD 的隶属函数

模糊输出值再通过与比例因子相乘转化到PID参数的基本论域中。设ΔKp的基本论域为［-2.7，2.7］，ΔKi为［-0.12，0.12］，ΔKd为［-0.00005，0.00005］。可得三个参数的比例因子为Gp=2.7/6、Gi=0.12/6、Gd=0.00005/6。三个修正参数与PID 控制器初始值相加后得到在线调整的新参数。

2.2 模糊推理

模糊规则的选取是设计模糊控制器的核心。实践中，模糊规则是根据工程设计人员知识和经验总结得出的，选择PID 三个输出参数应遵循以下控制规则[11]：

1）当|e|较大时，应取较大的Kp和较小的Kd（以使系统响应加快）且是Ki=0（为避免较大的超调，故取掉积分作用）。

2）当|e|中等时，应取较小的Kp（以使系统响应具有较小的超调），适当的Ki和Kd（特别是Kd的取值对系统的响应影响较大）。

3）当|e|较小时，应取较大的Kp和Ki（以使系统具有较好的稳态性能），Kd的取值要恰当，以避免在平衡点附近出现震荡。

本文根据模糊规则建立的模糊推理表见表1至表3。

表1 KP 模糊推理表

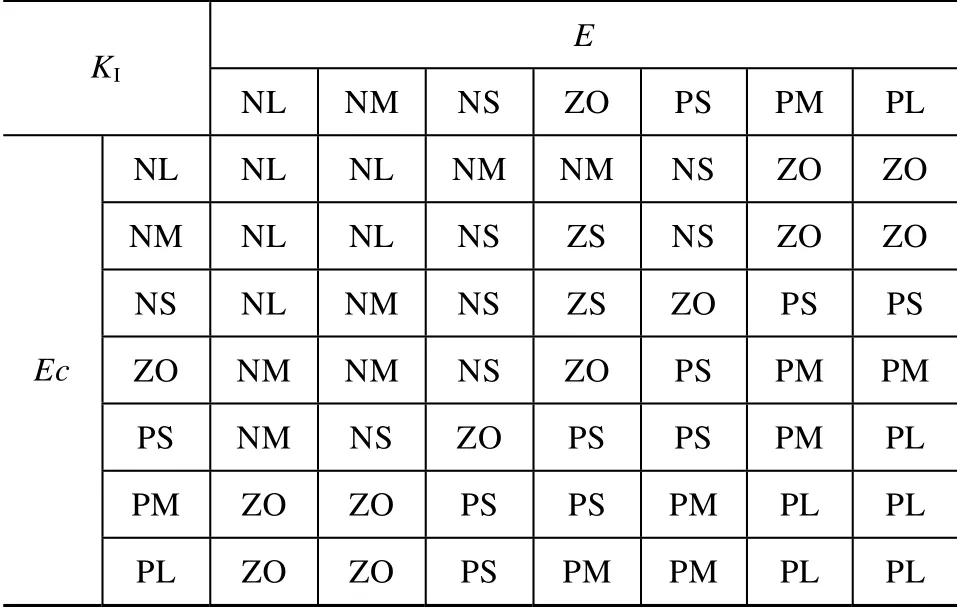
表2 KI 模糊推理表

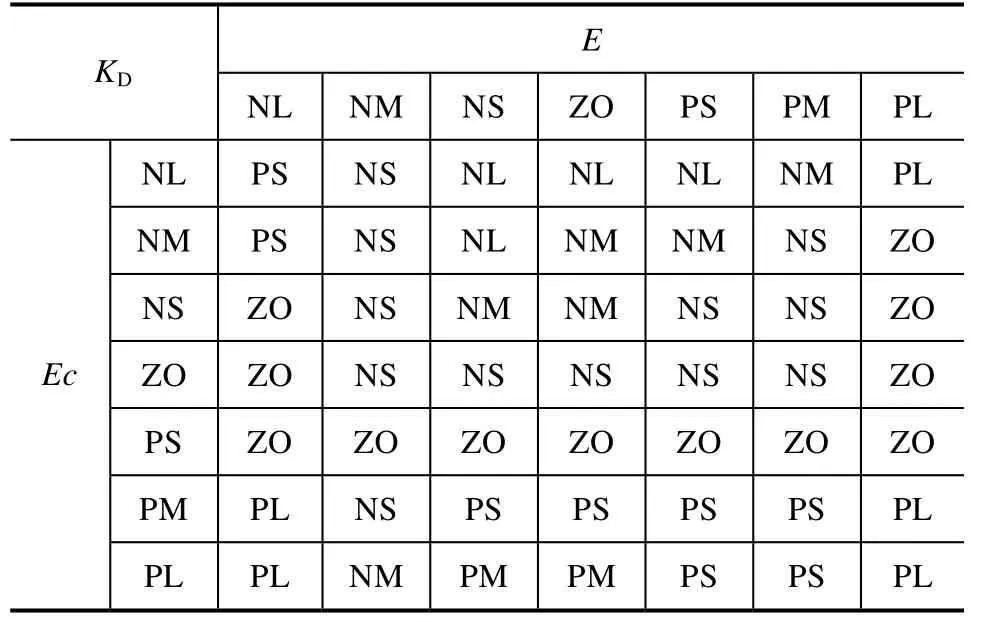
表3 KD 模糊推理表

3 系统仿真实验与分析

为验证本文所研究的内容，在Matlab/Simulink环境下，对摩擦系数F=0.02（N·m·s）的60kW 四相（8/6）SR 电机进行仿真。DITC 系统的开通角为35°，关断角为53°；内滞转矩为0.3，外滞转矩为0.5。图7给出了仿真系统总框图，其中FUZZY模块存放各参数隶属函数与模糊推理表，DITC 转矩滞环控制器模块根据上文所述原理用S 函数实现。

本文在给定负载转矩 10N·m、给定转速1000r/min 的条件下对电机传统电压PWM 控制、直接转矩（DTC）控制和直接瞬时转矩（DITC）控制三种控制策略进行仿真对比，得出转矩波形如图8所示。

考虑摩擦系数与给定转速，电机在给定负载转矩下的输出负载转矩为12.09N·m。由表4对比可知 DITC 控制策略的转矩波动范围最小，仅仅0.31N·m 的最大转矩误差远小于其他两种控制策略，能最大限度抑制转矩脉动。

为对比验证电机在DITC 控制系统下使用传统PID 控制器与模糊自适应PID 控制器的调速性能，本文取传统PID 控制器的参数值为Kp=0.8、Ki=0.1、Kd=0.00005，模糊自适应PID 控制器也以这组参数为自整定初值。在给定负载转矩10N·m、给定转速1000r/min 的条件下，图9（a）和（b）给出了使用两种PID 控制器情况下系统起动时转速响应波形图。

表5对比了两种PID 控制器的起动性能，考虑到电机实际起动时转矩不能过大，本文仿真对起动时转矩作了限幅，因此相较于起动中后期，模糊自适应PID 控制器的参数调节作用对起动初期时的影响相对较小，其结果是转速响应时间比传统PID 稍慢，但是前者大大的限制了转速超调量，且转速稳定时间快于后者，综合对比可以看出相较于后者，前者能够有效改善起动时的转速响应波形。

图7 基于模糊自适应PID 控制的开关磁阻电机直接瞬时转矩控制系统

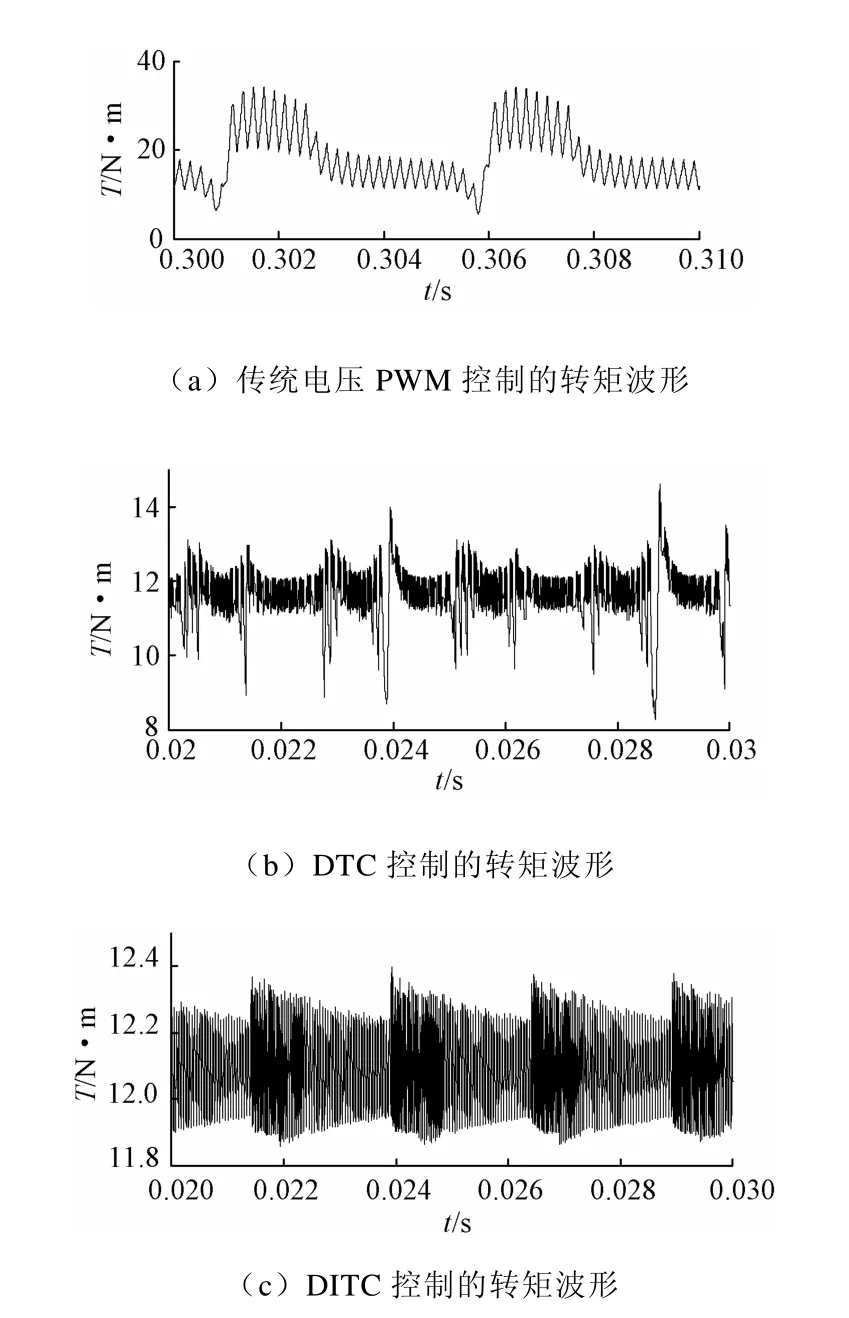
图8 三种控制方法的稳态转矩波形对比图

表4 三种控制方法稳态转矩性能指标

图9 系统起动时转速响应波形图

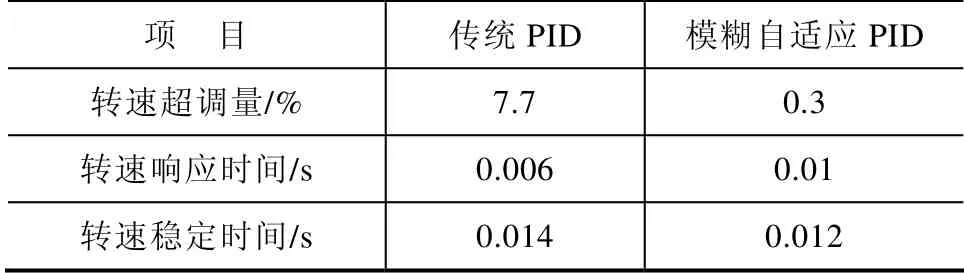
表5 系统起动性能对比

在给定负载转矩10N·m的条件下于0.1s 时加入大小为40N·m 的扰动负载，并于0.13s 时卸掉此负载，图10（a）和（b）为两种PID 控制方式在此情况下的转速响应波形图。由表6对比可知，模糊自适应PID 控制的抗干扰能力优于传统PID 控制，有更强的鲁棒性。

图10 系统负载变化时转速响应波形

表6 系统负载变化时转速响应性能对比

4 结论

本文在开关磁阻电机直接瞬时转矩控制策略的基础上引入了模糊自适应 PID 控制技术，并在Matlab/Simulink 环境下搭建了系统仿真模型，通过 比较可知相比于其他方法，直接瞬时转矩控制方法对抑制转矩脉动的作用明显；模糊自适应PID 控制器的引入又能有效改善系统调速性能，使系统在改善转矩性能的同时具有超调量低、转速稳定时间短、鲁棒性强的优点。

[1] 曹家勇,陈幼平,詹琼华,等.开关磁阻电动机控制技术的研究现状和发展趋势[J].电机与控制学报,2002,6(1): 1-5,25.

[2] 孙剑波,詹琼华,王双红,等.开关磁阻电机减振降噪和低转矩脉动控制策略[J].中国电机工程学报,2008,28(12): 134-138.

[3] 开关磁阻电机转矩脉动的智能抑制研究[J].微电机,2006,39(3): 7-10,14.

[4] 王勉华,梁媛媛,宋景哲,等.直接转矩控制在开关磁阻电机中的应用与研究[J].电机与控制应用,2008,35(2): 25-28,36.

[5] 夏长亮,王明超.基于RBF 神经网络的开关磁阻电 机单神经元PID 控制[J].中国电机工程学报,2005,25(15): 161-165.

[6] 王勉华,梁媛媛.开关磁阻电机直接转矩模糊PI 控制器设计[J].电气传动,2010,40(1): 51-54.

[7] 漆汉宏,张婷婷,李珍国,等.基于DITC 的开关磁阻电机转矩脉动最小化研究[J].电工技术学报,2007,22(7): 136-140.

[8] 罗兵,甘俊英,张建民.智能控制技术[M].北京: 清华大学出版社,2011.

[9] 霍建刚.基于模糊PID 控制的SRM 位置随动系统的分析与研究[D].天津: 河北工业大学,2011.

[10] 石辛民.模糊控制及其Matlab 仿真[M].北京: 清华大学出版社; 北京交通大学出版社,2008.

[11] 屈毅,宁铎,刘飞航,等.模糊PID 控制器的设计及其仿真[J].计算机仿真,2009,26(12): 130-132,176.

[12] 刘春元,王宗刚,张静,等.基于BP 网络SRM 的DITC 系统仿真研究[J].微电机,2011,44(12): 72-75.