基于数学形态学的行波奇异性 检测算法研究

王 丰 甘 燕

（三峡大学电气与新能源学院，湖北 宜昌 443002）

随着电力系统的发展，大容量、远距离的超（特）高压输电线路越来越多，电网结构日趋复杂，对系统的暂态稳定性也有了更高的要求。由于传统的基于工频量的继电保护装置在信号分析方面的局限性，其保护动作速度难以再有提高。而利用高频暂态量的行波保护不受系统运行方式等的影响，具有超高速动作特性，能满足大电网条件下系统的暂态稳定性的要求。

任何一套完整的保护装置都装有起动元件，它要求故障时可靠动作，非故障条件下不误动。故障发生后，线路上会产生电压电流行波，一定时间后到达保护安装处，并产生突变。但在实际线路中经常存在着干扰噪声信号，因此，快速有效的检测突变量和突变产生的时刻，即区分突变是由故障还是干扰噪声产生的，是起动保护算法的关键。

文献[1]利用故障行波和噪声行波在不同尺度下的小波变换表现的不同来加以区别，但它增加了计算量，不利于超高速保护的速动性。同时会减小波头的梯度，降低了灵敏度。文献[2]利用数学形态学滤波处理，然后用小波变换提取波头，取得了较好的效果。但是在脉冲序列距离行波波头较近或淹没行波波头时，会出现干扰梯度较大的情况，而导致误判。本文以数学形态学为基础，针对文献[2]中的不利情况提出了相应的改进措施，并以Matlab 仿真测试验证了本文措施的有效性。

1 数学形态学

数学形态学[3]建立在集合理论基础之上，是在对二维数字图像处理的研究中发展起来的。它能够很好描述图像的基本特征，可用来解决抑制噪声、特征提取、边缘检测等问题。数学形态学是一种非线性分析方法，不存在相移和幅度衰减等问题；与小波变换的频域分析相比，数学形态学着眼于波形形态，计算简单，仅有加减法和取极值运算，具有并行快速、易于硬件实现的优点。目前数学形态学在电力系统的一维信号处理方面得到了大量的应 用[4]。

基于数学形态学的开闭运算滤波器可有效滤除暂态行波中的噪声干扰。在完成滤波后，通过形态梯度可以检测出电流电压行波信号的突变时刻。

1.1 形态滤波

腐蚀与膨胀是数学形态学的基础，形态滤波和梯度运算[5]都由以上两者推导而出。腐蚀变换是一种收缩变换，使目标信号出现的外凸信号变得平滑，即减小外凸。相反，膨胀则是一种扩张变换，减小内陷信号。它们都是通过不同的结构元素完成对信号进行分析，修正信号的局部几何特征。

设f(n)和g(m)分别为待处理的离散数字信号和结构元素，D1和D2分别为f(n)和g(m)的定义域，则用结构元素g(m)对信号f(n)进行的腐蚀与膨胀分别定义为

由上述式（1）可以明显的看出，腐蚀与膨胀运算仅用了加减运算，对减少计算量是有裨益的。

结构元素g(m)是形态运算的重要组成部分，它起到“探针”的作用，收集信息。当探针不断移动时，就可以提取有用信息作分析。结构元素的设计如果不同的话，可以直接影响信号输出，因此它的设计取决于处理后要保持的信号的形状。对电力系统中具有衰减直流分量和各次谐波的工频正弦信号，常采用扁平结构元素，可以将结构元素的大小置零。

在腐蚀与膨胀的基础上，定义形态开运算[6]为结构元素g对信号f先进行腐蚀，然后再用结构元素g对腐蚀的结果(fΘg) 进行膨胀，得到结果(fΘg)⊕g。可以用公式表示如下：

而闭运算与开运算的腐蚀与膨胀顺序相反，可用公式表示为

式（2）和式（3）中的符号“·”和“·”分别表示开、闭运算。

在结构元素选择合适的条件下，开运算对受到外凸干扰信号的滤波效果较好，而闭运算则恰好相反，对受到凹陷干扰信号的滤波效果较好。但是在实际信号干扰中，两种类型的干扰都是存在的，单独应用开运算和闭运算作滤波器显然是不能满足要求的。于是利用开运算和闭运算各自的滤波优点，将二者以级联的形式形成新的滤波器，即“交替滤波”。根据结构元素g对信号f进行开运算和闭运算的顺序不同，可以得到开—闭运算和闭—开运算，分别记为Oc(f(n))和Co(f(n))表达式如下：

由于开运算和闭运算性质的不同，导致开一闭滤波器输出幅度偏小，而闭一开滤波器输出幅度偏大。在结构元素选择不合适时，单独使用二者之一并不能完全滤除外凸和凹陷干扰。因此，可采用合用二者，形成交替混合滤波如下：

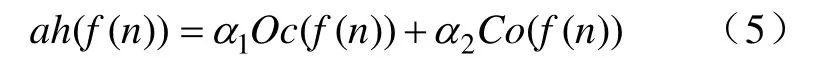
式中，α1和α2为加权系数，通过不断修正其值，可以得到最优滤波效果，但为简化算法通常取α1=2α=1/2[7]，即

在后续仿真中验证其滤波效果比较理想。

1.2 形态梯度

形态学梯度主要用于提取图像的边沿，本文中用于检测行波波形的突变特性，其基本运算以差分形式给出如下：

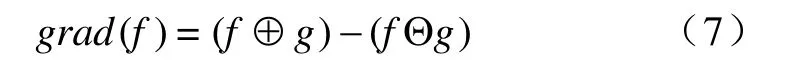
进行梯度运算前，对信号的滤波是十分有必要的。但结构元素的长度会影响到滤波效果和信号的奇异性检测。结构元素较长时，滤波效果较好，但奇异性检测效果不佳；结构元素较短时，效果恰好相反。所以，在形态梯度运算前，选择较长的结构元素，且长度以递增或递减方式呈现。而采用较短的结构元素来计算梯度。形态滤波及梯度运算表达如下：

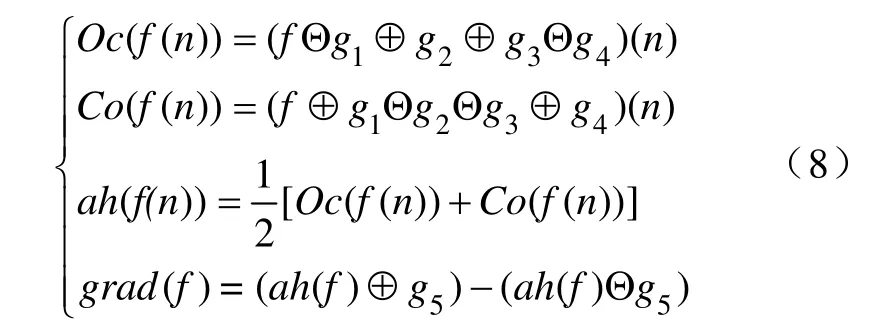
在仿真试验中g1,g2,g3,g4的长度分别为17、 27、37、47，g5的长度取3。

2 仿真试验

在Matlab/Simulink 中建立500kV 的输电线路模型，如图1所示。线路MN 为故障线路，LM、NR为非故障线路。线路参数为正序阻抗Z1=0.01273+ j0.2932Ω/km，负序阻抗Z1=Z2，零序阻抗Z0=0.3864+ j1.2957 Ω/km，线路对地正序电容与负序电容相等C1=C2=0.01274 μF/km，线路对地零序电容C0= 0.07751 μF/km。

图1 电力系统模型

图1中故障点F 在MN 线路内部距M 点65km处，仿真以A 相（左侧电源初相角60°）金属性接地故障为例，短路故障发生在仿真开始后的0.02s,结束于0.04s。采样频率设为1MHz。

在不加任何噪声干扰的情况下，进行凯伦贝尔相模变换，取1 模和2 模中较大者，并将故障时刻取为原点，绘制端电流行波波形如图2所示。

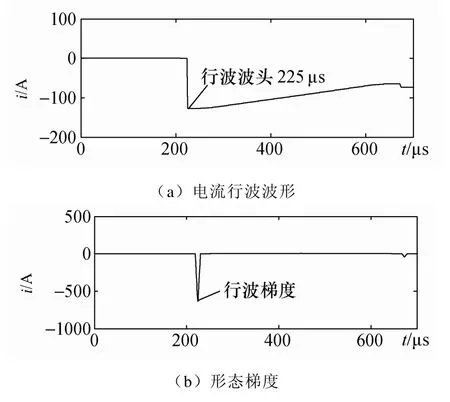
图2 理想状态下的仿真结果

由图1可以看出，行波波头在故障后225μs 时刻第一次到达M 端。根据实际参数：

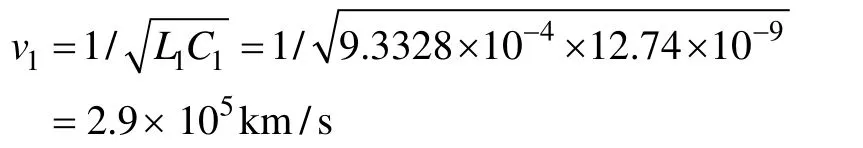
计算得到的时间为224μs，有1μs 的误差，但可忽略。

上述只是理想状态下的仿真结果，在实际系统中存在着各种噪声信号，下面分两种情况加入噪声信号，并进行形态滤波和梯度运算。考虑到进行滤波运算时，会削弱波头，在进行梯度运算时增加了改进梯度算法[8]。

1）在电流行波中加入混有信噪比为10dB 的高斯白噪声和脉冲序列的干扰，但脉冲序列与行波波头相距较远，检查形态滤波效果，并利用形态梯度提取行波突变点，绘制波形如图3所示。

图3 加入噪声后的仿真结果1

2）在电流行波中加入混有信噪比为10dB 的高斯白噪声和脉冲序列的干扰，但脉冲序列与行波波头相距较近，检查形态滤波效果，并利用形态梯度提取行波突变点，绘制波形如图4所示。

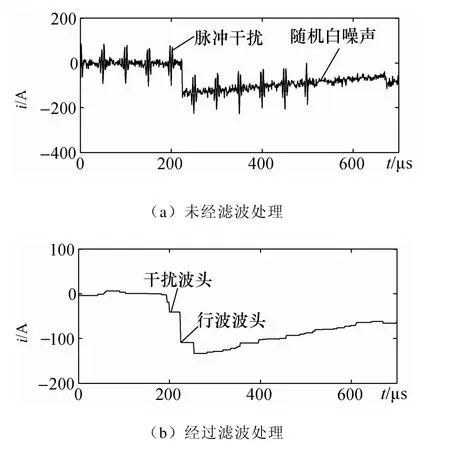
图4 加入噪声后的仿真结果2

3 结果分析及改进

通过比较图2至图4的波形结果，可以发现数学形态学在滤除噪声干扰方面效果显著，也能比较灵敏的提取突变点，如图3所示。但是，在一些情况下，如图4，即当，有较大脉冲信号出现在行波波头附近时，经滤波后，脉冲干扰波头也会出现，且行波波头梯度减小，这对准确提取故障时刻不利，同时也会影响到起动元件的灵敏性。在此提出相应的改进方法，来消除或减小该不利影响。

鉴于从前述仿真中，在即使出现阶梯波，但行波波头仍然较大于干扰波头的情况下，本文受模极大值[9]的启发，计算滤波后某一邻域内的极大值，而将邻域内其他点置零，消除因出现阶梯波带来的不利因素，可表达为

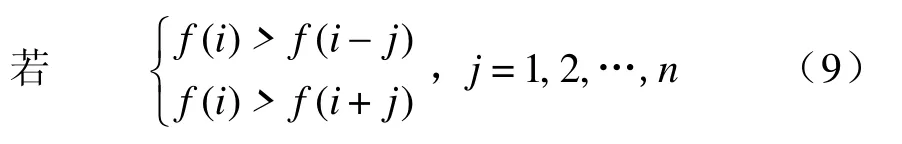
则保留f(i)的值，而将f(i)前后共2n个点置零，这样就可以消除行波波头附近出现阶梯波，而留下故障行波波头。本文中n取30。从对图4（c）中作上述处理的图5中可以看出该方法效果明显，能排除不利因素。

图5 改进后的形态梯度

4 结论

本文在阐述数学形态学的一些基本运算的基础上，通过仿真验证了数学形态学在滤波和奇异性检测方面的优越性。针对系统中有可能出现的导致起动元件误动或使灵敏度降低的情况提出了改进措施，仿真结果验证了该改进措施能排除干扰，准确地检测波头到达时刻。但在某些极端情况下，如电压过零点时该方法将出错。如果考虑到极端不利情况出现的几率[10]，该方法还是十分有效的，因此本文对准确提取突变点，保证故障时保护可靠动作，干扰时不误动有积极作用。

[1] 董新洲,贺家李,葛耀中.小波变换在行波故障检测中的应用[J].继电器,1998,26(5): 3-6.

[2] 林湘宁,刘沛,刘世明,等.电力系统超高速保护的形态学-小波综合滤波算法[J].中国电机工程学报,2002,22(9): 19-24.

[3] 崔屹.图像处理与分析——数学形态学方法及应用[M].北京: 科学出版社,2000.

[4] 尹文琴,刘前进.数学形态学在电力系统中的应用综述[J].继电器,2007,35(19): 76-83.

[5] 袁兆强.超高压交流输电线路行波电流积分差动保护算法研究[D].武汉: 武汉大学,2013.

[6] Maragos P,Schafer R W.Morphological filters–Part I: Their set-theoretic analysis and relations to linear shift-invariant filters[J].IEEE Trans.on Acoustics,Speech,and Signal Processing,1987,35(8): 1153- 1169.

[7] 赵青春,邹力,刘沛.基于数学形态学的线路超高速方向保护[J].电网技术,2005,29(21): 75-80.

[8] 魏军,罗四倍.基于信号奇异性检测的行波起动元件算法的探讨[J].继电器,2007,35(21): 1-6.

[9] 胡铭,陈珩.基于小波变换模极大值的电能质量扰动检测与定位[J].电网技术,2001,25(3): 12-16.

[10] 葛耀中.新型继电保护与故障测距原理与技术[M].西安: 西安交通大学出版社,1996.