一类具有标准发生率的SIRS传染病模型分岔分析*
2015-05-25刘苏雨蒋贵荣凌琳
刘苏雨 蒋贵荣 凌琳
(桂林电子科技大学数学与计算科学学院,桂林 541004)
引言
疾病发生率是刻画传染病模型的主要内容,经典的传染病模型大多是采用双线性发生率[1]和饱和发生率[2].标准发生率[3]属于非线性发生率,这种发生率可以包括行为变化和群体效应,Anderson和May[4]通过研究证实,对于某些动物来说,标准发生率比双线性发生率更符合实际.
连续动力系统的分岔理论研究已较为丰富,而对于脉冲动力系统的分岔研究很少.蒋贵荣等[5]研究了一类自治脉冲微分方程,得到了由半平凡解分岔出正周期-T解的fold分岔;钱临宁和陆启韶在文[6]中得到了系统的半平凡解到正周期-T解的跨临界分岔行为;文[7]分析了由平凡解分岔出非平凡周期-T解的超临界分岔现象,等等.但是对于由平凡解分岔出正周期-T解的分岔现象大多没有考虑.
垂直传染、脉冲接种[8]和脉冲生育[9]常被用来建立和研究传染病模型.本文同时考虑垂直传染、脉冲接种和脉冲生育,建立一个有标准发生率的传染病模型,利用映射研究该模型正周期解的存在性及该系统的分岔现象.
1 模型描述
设S(t),I(t)和R(t)分别为t时刻的易感者、感染者和移出者的数量,现给出有脉冲生育和接种、垂直传染和标准发生率SIRS的传染病模型:
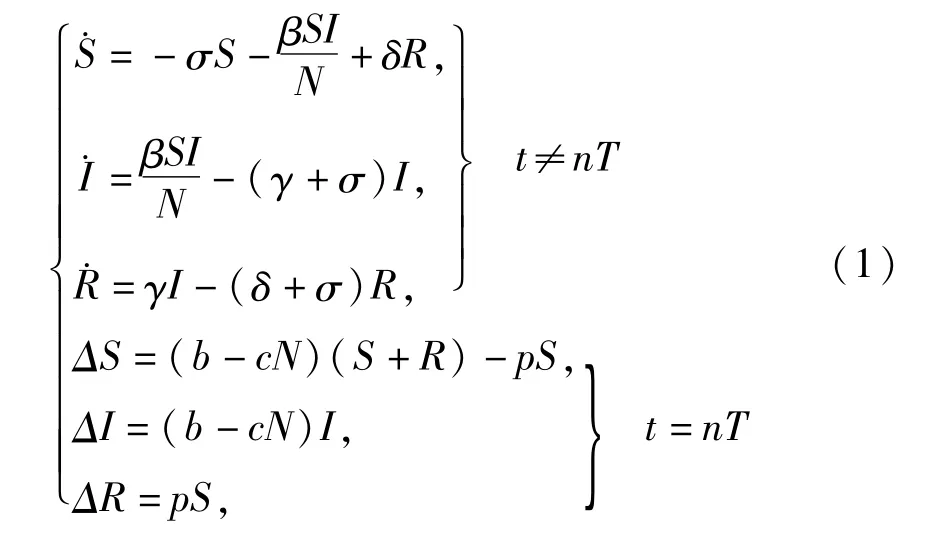
其中,σ表示自然死亡率且有0<σ≤1,δ是移出者丧失免疫进入易感者类的比率,γ是感染者的自然恢复率,βSI/N是标准发生率,生育脉冲为ΔN=(b-cN)N,其中b是最大出生率.染病者的后代均为染病者,易感者和移出者的后代均为易感者.在生育时刻,ΔS=(b-cN)(S+R),由于垂直传染,ΔI=(b-cN)I.易感者的接种率为p,即 ΔS=-pS,ΔR=pS,其中0<p<1.
2 无病周期-T解和平凡解的存在、稳定性
当种群中不存在感染者,即I(t)=0(t>0)时,N(t)=S(t)+R(t),系统(1)变为:

设系统(2)的轨线从(Nk,Rk)出发,在T时刻到达点然后跳到(Nk+1,Rk+1),则有映射

离散映射(3)的不动点为
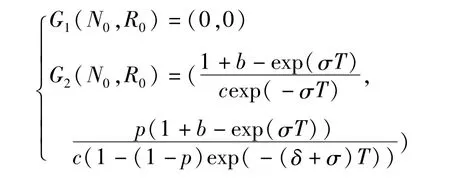
由G2(N0,R0)可得系统(1)无病周期解为
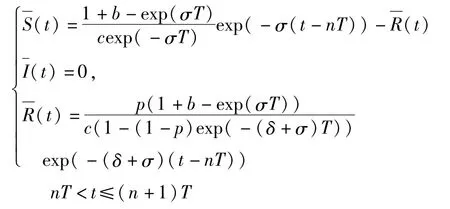
由于N(t)=S(t)+I(t)+R(t),由(1)有:

由系统(4)在无病周期-T解处的变分系统对应的特征值为:

因为0<p<1,(δ+σ)T>0,所以|λ2|<1.当|λ1|<1,|λ3|<1时,无病周期-T解渐近稳定.由得|λ1|<1:
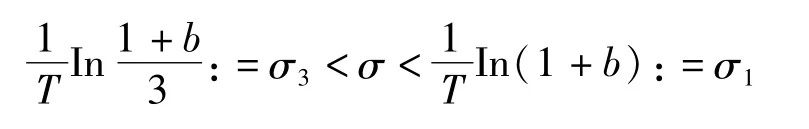
假设 β>γ,由|λ3|<1得:
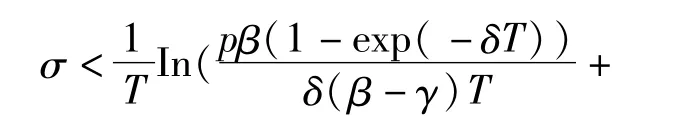
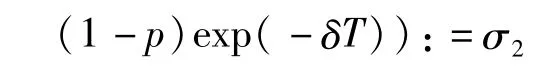
在本文中总假设下列条件成立,

当 σ∈(σ3,σ1)时,有|λ3|>1;当 σ∈(0,σ2)时,有|λ1|>1;当 σ∈(σ2,σ3)时,有|λ1|>1和|λ3|>1对任意的σ∈(0,1],总有模大于1的特征值,从而(1)的无病周期-T解是不稳定的.
过G1(N0,R0)=(0,0)的系统(1)平凡解(0,0,0)处对应变分系统的单值矩阵的乘子是:
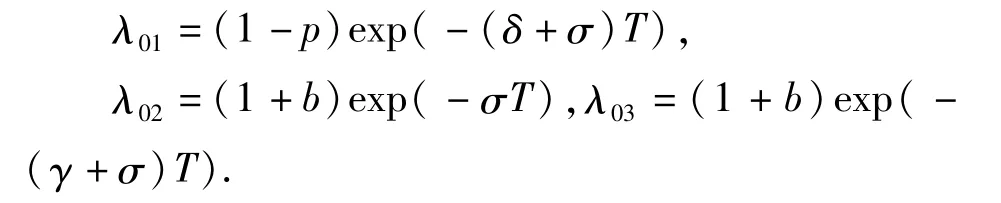
当 σ∈(σ1,1]时,|λ01|<1,|λ02|<1,|λ03|<1,从而平凡解稳定;当 σ∈(0,σ1]时,|λ02|>1从而平凡解不稳定.于是我们有下面的结论:
定理2.1假设(5)成立,(1)的平凡解在 σ∈(0,σ1]下是不稳定的,在σ∈(σ1,1]下是稳定的;(1)的无病周期-T解在σ∈(0,1]下是不稳定的.
3 分岔
取μ=-σ为参数,讨论(1)的周期解的分岔.
3.1 跨临界分岔现象
对于μ1=-σ1和I(t)=0.由σ1=μ+In(1+b)/T得由(3)得

映射(6)的一个中心流形可以表示为:

则限制在中心流形上的映射为:

在点
由文献[10]中的跨临界分岔的判定可知,系统(4)在μ=μ1=-σ1处发生跨临界分岔,系统的平凡解在μ=μ1=-σ1分岔出周期-T解.由于δ>0,当 μ∈(μ1,μ1+ε)时,系统没有稳定的无病周期-T解,故此时原系统的平凡解在μ=μ1=-σ1分岔出稳定的正周期-T解.
定理3.1系统(1)在 μ=μ1=-σ1处发生跨临界分岔,平凡解分岔出正周期-T解,即ε>0,当μ∈(μ1,μ1+ε)时,系统(1)有稳定的正周期-T解.
3.2 Flip分岔现象
假设系统(4)的周期-T解(N(t),I(t),R(t))从点A0(N0,I0,R0)出发,到达B0(N(t),I(T),R(T)),再跳到A0,有R0=p(N(T)-I(T))+(1+p)R(T),N0=(1+b-cN(T))N(T),I0=(1+b-cN(T))I(T),由N·=-σN得到N(T)=N0exp(-σT),于是N0=(1+b-exp(σT))exp(σT)/c.
现取Poincaré截面S0={(N,I,R)|I=I0},过初始点Ak(N0+xk,I0,R0+yk)的解为(N1(t),I1(t),R1(t)),其中Ak∈S0.在时刻T解到达Bk=(N1(T),I1(t),R1(t)),再然后跳到点Ak+1(N0+xk+1,I0,R0+yk+1).
令x(t)=N1(t)-N(t),y(t)=R1(t)-R(t),z(t)=I1(t)-I(t).则x(t),y(t),z(t)满足下面的关系:
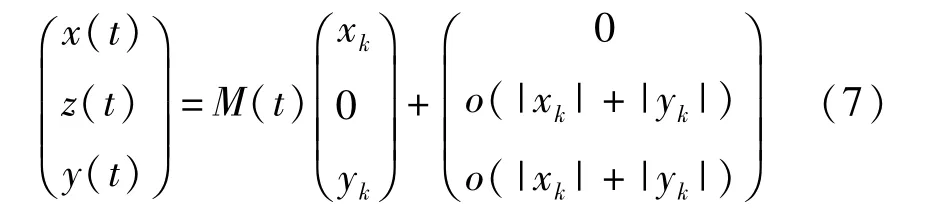
其中M(t)满足

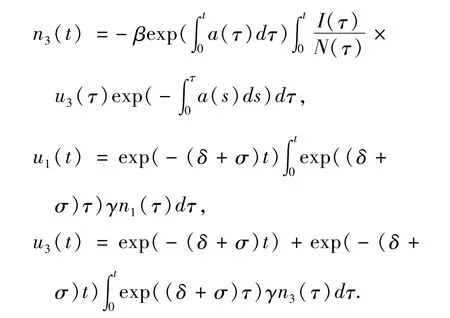
由(7)得:

从而得到Poincaré映射:

其中:
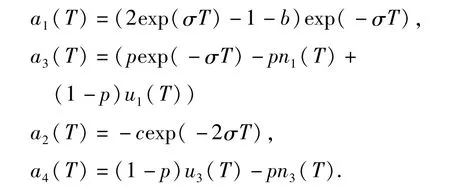
式(8)的不动点的特征值为:

当时,λ4=a1(T)=-1.
定理3.2 系统在μ=μ3=-σ3处发生flip分岔.
证明:令=μ-μ3=μ+σ3,则(8)可以写成:

可计算出一个限制在中心流形上的映射为:
f:x|→(2-3expx-在点处有
由文献[11]中定理3.5.1可知:系统在 μ=μ3=-σ3处发生flip分岔,从而 ε>0,当 μ∈(μ3,μ3+ε)时,系统有稳定的正周期-2T解.定理得证.
4 数值模拟
在(1)中,取b=2.8,T=2,δ=0.4,p=0.2,c=0.2,β=0.6,γ=0.5.则 μ1=-σ1≈-0.6675,μ2=-σ2≈-0.0851,μ3=-σ3≈-0.1182.显然条件(5)成立.以 μ(-σ)为参数,系统(1)的周期解的分岔如图1所示,当 μ∈[-1,-0.6675]时,系统有稳定的平凡解,系统在μ=μ1=-σ1处发生跨临界分岔,当μ从μ1左侧变到右侧时,系统出现稳定的正周期-T解,系统在μ=μ3=-σ3处发生flip分岔,由正周期-T解分岔出正周期-2T解,很好的验证了定理3.1和定理3.2.图2给出了(1)在μ=-σ=-0.4时的正周期-T解.
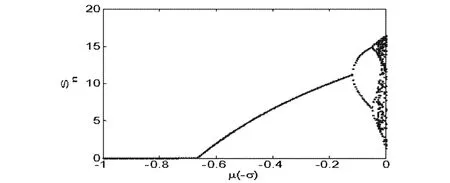
图1 系统(1)关于μ的分岔图Fig.1 The bifurcation diagram of periodic solutions of system(1)with respect to parameterμ
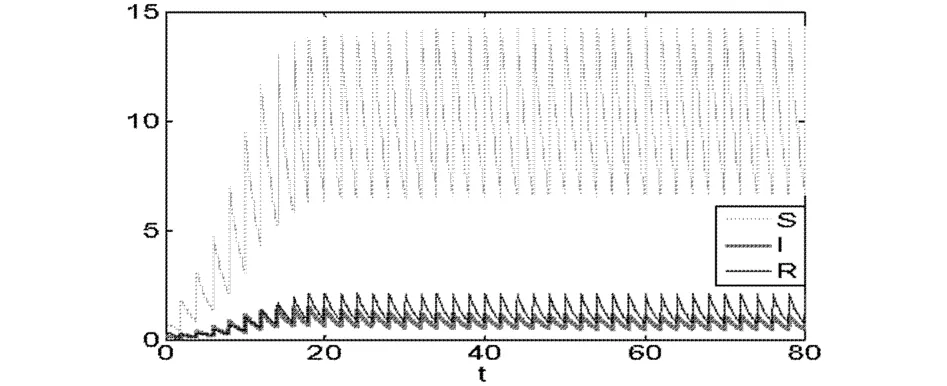
图2 μ=-0.4时的系统(1)的解的时间序列图Fig.2 The time-series of S,I and of(1)withμ=-0.4
5 结论
本文讨论了对所建的系统在β>γ的情形下,由于参数间的变化使得σ2<σ3<σ1下的系统的动力学性质.随着参数μ=-σ的增加,系统在μ=μ3=-σ3处发生跨临界分岔,由平凡解分岔出正周期-T解;在μ=μ3=-σ3处发生flip分岔,由正周期-T解分岔出正周期-2T解.
随着σ的变化,系统出现不同的稳定周期解,说明了自然死亡率大小在传染病的控制过程中的作用,为控制传染病的传播提供了一定的理论依据.
1 屈林波,韩瑞珠.一类具有迁移特性的生物危险源扩散动力学模型分析.东南大学学报(自然科学版),2007,37(II):381~386(Qu L B,Han R Z.Analysis of biology dangerous source diffusing dynamicsmodel in populationmigration.Journal of Southeast University(Natural Science E-dition),2007,37(II):381~386(in Chiniese))
2 庞国萍,陈兰荪.具饱和传染率的脉冲免疫接种SIRS模型.系统科学与数学,2007,27(4):563~572(Pang G P,Chen L S.The SIRS epidemic model with saturated contact rate and pulse vaccination.Journal of Systems Science and Mathematical Sciences,2007,27(4):563~572(in Chiniese))
3 Hu Z X,Liu S,Wang H.Backward bifurcation of an epidemic model with standard incidence rate and treatment rate.Nonlinear Analysis:Real World Applications,2008,9:2302~2312
4 Anderson R,May R.Infectious diseases of humen:dynamics and control.Oxford:Oxford University Press,1991
5 蒋贵荣,陆启韶,钱临宁.一类脉冲动力系统的状态反馈控制.动力学与控制学报,2005,3(4):17~23(Jiang G R,Lu Q S,Qian L N.State feedback control of a class of impulsive dynamic systems.Journal of Dynamics and Control,2005,3(4):17~23(in Chiniese))
6 钱临宁,陆启韶.一类自治脉冲微分方程的动力学研究.动力学与控制学报,2008,6(2):97~101(Qian L N,Lu Q S.Dynamics of a class of autonomous impulsive equations.Journal of Dynamicsand Control,2008,6(2):97~101(in Chiniese))
7 Zhang H,Paul Georgescu,Chen L S.On the impulsive controllability and bifurcation of a predator-pest model of IPM.BioSystems,2008,93:151~171
8 Gakkhar S,Negi K.Pulse vaccination in SIRS epidemic modelwith non monotonic incidence rate.Chaos,Solitons and Fractals,2008,35:626~638
9 韩丽涛.两种群相互竞争具有脉冲出生率的SIS传染病模型.生物数学学报,2006,21(2):237~246(Han L T.An SIS epidemic model of two competitive species with birth pulse.Journal of Biomathematics,2006,21(2):237~246(in Chiniese))
10 Wiggins S.Introduction to applied nonlinear dynamical systems and chaos.New York:Springer-Verlag,1990
11 Guckenheimer J,Holmes P.Nonlinear oscillations,dy-namical systems,and bifurcations of vector fields.New York:Springer-Verlag,1983
