关于正弦起搏器控制耦合神经元的去同步探索*
2015-05-25李美生陈偲张红慧
李美生 陈偲† 张红慧
(1.北京航空航天大学数学与系统科学学院,北京 100191)(2.北京航空航天大学航空科学与工程学院,北京 100191)
引言
近年来,耦合神经元系统的同步成为国内外学者们研究的焦点,出现了新兴的神经动力学.神经元的同步在大脑的信息处理过程中发挥了至关重要的作用[1].然而并非所有的同步模式都是有利的.过度的同步往往会导致某类生理疾病[2-3],例如帕金森氏症、手的颤抖和癫痫病,这种同步称为病态同步.脑深部刺激治疗(脑起搏器)是近年来帕金森病治疗中最大的突破.它通过植入体内的脑起搏器发放弱电脉冲,刺激脑内控制运动的相关神经核团,抑制引起帕金森病症状的异常脑神经信号从而消除了帕金森病的症状[4-6].同步和不同步之间的转化是为了适应系统机能调节的形态改变[7].因此,对神经元间的同步和去同步化机制的研究都是很有意义的.
目前,神经元耦合系统的同步问题的研究有着较丰富的结论[8-11].而去同步方面的研究则相对较少,Popovych等[12-13]提出了利用非线性延迟反馈控制可以有效地消除神经系统的病态同步,于海涛等[14]在该方法的基础上采用差分反馈和直接反馈实现了离散神经元网络的去同步化.于洪洁等[15]利用正弦延迟反馈法对单个HR神经元模型的动力学特性进行了研究,发现对HR神经元进行反控制的正弦延迟自适应反馈法是有效的.目前的耦合神经元去同步研究都没有专门针对去同步的系统去同步性程度的分类和度量.
本文针对两个全同HR神经元的耦合系统,采用正弦起搏器控制其中一个神经元的方式来达到系统的去同步化,对丰富的去同步效果进行分类,并设计相应的度量指标,最后使用这些指标对正弦起搏器控制下的神经元耦合系统进行进一步的数值分析.
1 去同步系统模型
考虑两个全同HR神经元N1和N2通过双向电突触耦合,其中N1受到起搏器的控制,如图1.本文中,起搏器对神经元的控制是在神经元的外界直流刺激上再加入一个较弱的正弦的交流信号.它们的动力学行为由以下微分方程描述:

其中,x代表神经细胞的膜电位,y是与内电流(例如Na+和K+)相关的恢复变量,z表示与Ca2+激活的K+离子电流相关的慢变调节电流,I表示外界直流激励.a,b,c,d,r,s以及 χ都是常数,取值参考文献[10].C是神经元N1和N2之间的耦合强度,C0是起搏器对神经元N1的控制强度,T是起搏器控制神经元N1加在外界直流刺激上面的正弦信号的周期.

图1 带有起搏器的两个全同神经元耦合系统示意图Fig.1 The diagram for the two identical neurons coupled system with a pacemaker
令
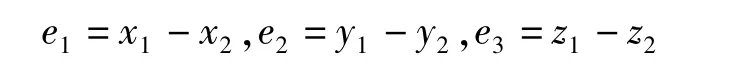
得到如下误差方程:

(e1,e2,e3)=(0,0,0)不是此方程的零解,此时对于任意初始条件,两个神经元都不能完全同步.所以只要起搏器对神经元的膜电位激励不恒等于零,那么就对上述系统具有一定的去同步效果.
2 去同步类型
对于由(1)式定义的系统,不同的起搏器参数C0、T会使得神经元N1和N2之间的去同步性出现很大差别.图2显示,逐渐增大起搏器耦合强度C0时,两个神经元的同步性受到了不同程度的破坏.当系统的其他参数发生变化时,系统会出现更为多变的去同步情况.图3中可见,正弦起搏器控制下的神经元耦合系统出现了其中一个神经元周期性出现静息态、两神经元都转迁成周期簇放电、其中一个神经元转迁成周期簇放电三种情况.
I=1.4时的单个HR神经元的放电模式应该是周期峰放电,图3(a)中的两个耦合HR神经元的放电模式在起搏器控制下仍然是周期峰放电,它们的峰峰间期(ISI)只有不大的个体差别,它们的平均峰峰间期仍然相等.可见这两个神经元还有较强的同步性,我们姑且把这种两个神经元的峰放电时间不完全相等,而平均峰峰间期相等且神经元放电模式保持去同步以前的模式的去同步情况叫做“弱去同步”.对比图3中的(a)和(b)两种去同步效果,由于(b)情况中两个神经元放电的平均峰峰间期已经不相等了,所以我们认为:(b)情况中两个神经元的同步性得到了很大的削弱,去同步性远远强于(a)情况.因此,我们将这种两个神经元放电的平均峰峰间期不相等,且神经元放电模式保持去同步以前的模式的去同步情况叫做“强去同步”.图2中的(c)情况中,神经元N1的放电模式发生了转迁,变成了周期簇放电,两个神经元之间的同步性也受到了很大程度的削弱.同样,图3中的三种情况中,神经元的放电模式也都发生了不同程度的转迁.于是,我们将这些神经元的放电模式发生了改变的情况统称为“破坏性去同步”.

图2 I=1.4、T=180、C=0.02时,系统(1)的膜电位时间历程图(a)C0=0.01,(b)C0=0.03,(c)C0=0.05Fig.2 The time course of system(1),I=1.4、T=180、C=0.02(a)C0=0.01,(b)C0=0.03,(c)C0=0.05
3 去同步效果的度量
为了便于对上文中的去同步情况进行更加细致的研究,我们对“弱去同步”和“强去同步”设计了一些指标来量化去同步性的大小,由于“破坏性去同步”具有很强的多样性,并且这种改变的神经元原有放电模式的去同步是我们不愿意看到的,所以我们没有对“破坏性去同步”设计度量指标.在系统“弱去同步”的前提下,我们利用神经元的峰峰间期来构造度量指标.这个指标为Q1,定义如下,若两个神经元的峰峰间期分别是F1n、F2n(n=1,2,3…),N→+∞,则:
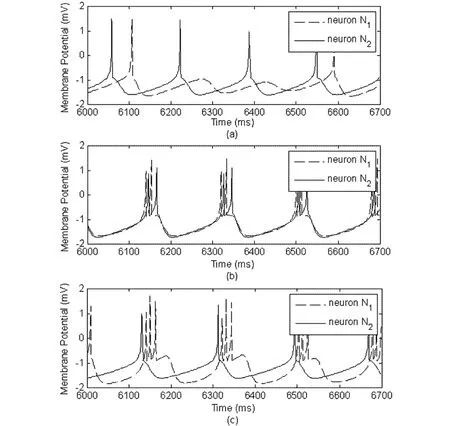
图3 I=1.4、T=180时,系统(1)的膜电位时间历程图(a)C=0.02,C0=0.02,(b)C=0.08,C0=0.08,(c)C=0.04,C0=0.3Fig.3 The time course of system(1),I=1.4、T=180(a)C=0.02,C0=0.02,(b)C=0.08,C0=0.08,(c)C=0.04,C0=0.3
在系统“强去同步”的时候,平均峰峰间期不相等,神经元的放电次数也不等,因此不能使用Q1作为指标.由于“强去同步”具有神经元的平均峰峰间期不相等的特点,所以以此构造度量指标.平均峰峰间期的不同也就意味着放电次数不同,于是如下定义指标Q2,令两个神经元在0~t时间内的峰放电次数分别是B1(t)和B2(t),t→∞,则:
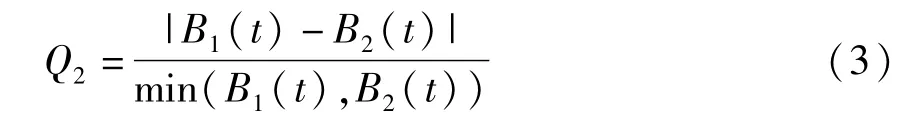
于是有:“弱去同步”时,Q1值越大则去同步性越大;“强去同步”时,Q2值越大则去同步性越大;Q1和Q2的值始终为非负数.
我们现在对(1)式定义的系统进行数值模拟,计算出不同参数下去同步度量指标Q1和Q2的值.由于度量指标定义中N和t的取值都是正无穷大,并且系统在非“破坏性去同步”的时候不会出现混沌现象,所以在一定误差范围内,我们认为系统进入周期状态,以此计算度量值.为了便于观察,我们令“弱去同步”时,Q2=-0.01;令“强去同步”时,Q1=-0.02;令“破坏性去同步”时,Q1=-0.03,Q2=-0.03.
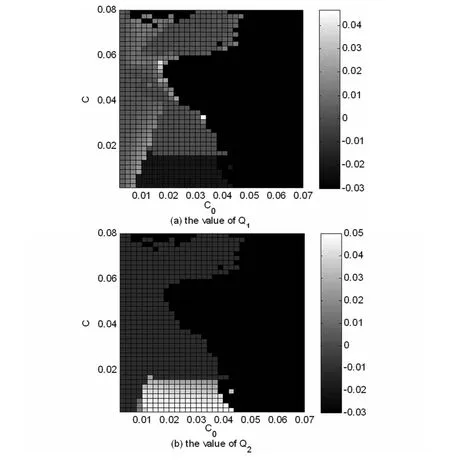
图4 I=1.4,T=165时,系统(1)的度量指标值Fig.4 The value of system(1)’smetric indexes,I=1.4、T=165
从图4中可以看到,当C<0.016时,随着C0增大,系统依次出现“弱去同步”、“强去同步”、“破坏性去同步”;当C>0.016时,随着C0增大,系统的去同步程度直接从“弱去同步”变成“破坏性去同步”;而当C=0.016时,随着C0增大,系统依次出现“弱”、“强”、“弱”、“破坏性”去同步.因此C=0.016是T=165的系统的去同步性态的一条明显分隔线.其次,在0<C<0.026、0.014<C0<0.038的这一范围内,Q1和Q2对C变化的敏感性远远大于C0的敏感性,即此时Q1和Q2几乎只受C影响.还可以看到,当C0>0.05时,无论C取何值,系统一定出现“破坏性去同步”.
由于I=1.4时,单个HR神经元的峰放电间期约为156,上面的仿真结果是起搏器周期T大于原神经元放电周期的结果,因此我们又做了T小于156时的数值仿真,如图5.可见,T=150时:“弱去同步”有两块严格分离的区域,其中一块“弱去同步”区域完全处于“破坏性去同步”的包围中,形成孤岛;仍然存在一个参数范围,使得这个参数范围内中的指标值对C变化的敏感性远远大于对C0的敏感性;系统不再具有一条明显的去同步性态分隔线.

图5 I=1.4,T=150时,系统(1)的度量指标值Fig.5 The value of system(1)’smetric indexes,I=1.4、T=150
4 小结
正弦起搏器能有效控制神经元去同步,本文通过用正弦起搏器刺激单个神经元的方式对两个全同HR神经元耦合系统进行了去同步探索,实现了丰富的去同步效果.仿真结果表明:系统(1)中的参数I=1.4,T=165时,起搏器耦合强度只要大于0.05就能破坏原神经元的放电模式;一定参数范围内,去同步效果对神经元耦合强度变化的敏感性远远大于正弦起搏器耦合强度;总能找到参数使得系统出现“破坏性去同步”.本文的结果对耦合神经元的去同步研究具有参考价值.
1 Masuda N,Aihara K.Global and local synchrony of coupled neurons in small-world networks.Biological Cybernetics,2004,90:302~309
2 Freund H J,Motor unit and muscle activity in voluntary motor control.Physiological Reviews,1983,63:387~436
3 Levy R,Hutchison W D,Lozano A M,et al.High-frequency sync-hronization of neuronal activity in the subthalamic nucleus of parkinsonian patients with limb tremor.Journal of Neuroscience,2000,20:7766~7775
4 胡小吾,周晓平,王来兴等.丘脑底核脑深部刺激术治疗帕金森病的手术方法和疗效分析.中国神经精神疾病杂志,2003,29(6):407~409(Hu X W,Zhou X P,Wang L X,et al.Technical approach and effects of deep brain stimulation of the subthalamic nucleus in parkinson’s disease.Chinese Journal of Nervous and Mental Diseases,2003,29(6):407~409(in Chinese))
5 孙成彦,孙伯民,潘力等.脑深部电刺激治疗帕金森病的并发症分析.中国神经精神疾病杂志,2003,29(6):410~413(Shun C Y,Shun B M,Pan L,et al.Complication of DBS in the treatment of parkinson’s disease.Chinese Journal of Nervousand Mental Diseases,2003,29(6):410~413(in Chinese))
6 邰超,罗明,肖登明等.应用Washout filter控制耦合神经元同步活动.工业控制计算机,2010,23(8):81~84(Tai C,Luo M,Xiao D M,etal.Controlling synchronous behaviors of coupled neurons by washout filter.Industrial Control Computer,2010,23(8):81~84(in Chinese))
7 Steinmeta P N,Roy A,Fitzgerald P J,et al.Attention modulates synchronized neuronal firing in primate somatosensory cortex.Nature,2000,404:187~190
8 Wang Q Y,Lu Q S,Wang H X.Transition to complete synchronization in two coupled chaotic neurons.Chinese Physics,2005,14:2189~2195
9 Shi X,Lu Q S.Phase synchronization in electrically coupled different neuronal pacemakers with the Chay model.Chinese Physics Letters,2005,22:547~550
10 Li M S,Lu Q S,Duan L X,Wang Q Y.Firing patterns and transitions in coupled neurons controlled by a pacemaker.Chinese Physics Letters,2008,25(8):2806~2808
11 郑艳红,陆启韶.时滞影响下的环式耦合混沌神经元同步.动力学与控制学报,2008,6(3):208~212(Zheng Y H,Lu Q S.Synchronization in ring coupled chaotic neuronswith time delay.Journal of Dynamicsand Control,2008,6(3):208~212(in Chinese))
12 Popovych O V,Hauptmann C,Tass PA.Effective desynchronization by nonlinear delayed feedback.Physical Review Letters,2005,94(16):164102
13 Popovych O V,Hauptmann C,Tass PA.Control of neuronal sync-hrony by nonlinear delayed feedback.Biological Cybernetics,2006,95:69~85
14 于海涛,王江,车艳秋等.非线性时滞反馈实现离散神经元网络的去同步化.动力学与控制学报,2010,8(4):375~379(Yu H T,Wang J,Che Y Q,et al.Nonlinear delayed feedback for effective desynchronization of discrete neural network.Journal of Dynamics and Control,2010,8(4):375~379(in Chinese))
15 于洪洁,张文龙,童伟君.H-R神经元的正弦函数-延迟反馈反控制.医用生物力学,2012,27(2):233~237(Yu H J,Zhang W L,Tong W J.Anti-control of sine function-delay feedback for H-R neuron.Journal ofMedical Biomechanics,2010,8(4):375~379(in Chinese) )
