一个带负顾客排队系统算子的半群特征

奥古丽江·艾尼

（乌鲁木齐市第二中学，新疆乌鲁木齐830000）

一个带负顾客排队系统算子的半群特征

奥古丽江·艾尼

（乌鲁木齐市第二中学，新疆乌鲁木齐830000）

利用泛函分析中的线性算子半群理论讨论一个带负顾客的非空竭服务休假排队系统模型相应算子的半群特征。结果表明该排队模型相应的算子生成一个正定压缩C0-半群S（t）。

带负顾客的排队系统；Cauchy问题；线性算子；耗散算子

线性算子半群理论是研究排队系统和可靠性系统的理论基础和重要工具，尤其是在讨论系统解的存在唯一性、渐近性和稳定性等方面发挥着重要的作用［1-12］。与此同时，利用数学模型的方法，研究、评价排队系统在内的各类系统的可靠性已经成为可靠性理论及可靠性数学的热门课题。随着排队论的发展，90年代左右产生了一类新型的排队系统，即带负顾客排队系统。负顾客是一种全新的顾客，他们相对于一般（正）顾客而言的，他们本身不需要系统提供的任何服务，负顾客到达后，若系统是空闲的则立刻从系统中消失，若系统中有接受服务的正顾客，则立刻把他带走。负顾客通常被认为是一次操作失误，外来信号的干扰，一种病毒，工作信号的消失等等。负顾客概念的提出，使许多计算机、控制、机械和交通等领域中的各类现实问题找到了解决问题的方法，引起了国内外研究者的广泛关注，从而对负顾客排队进行了一系列的研究。在文献［13］中作者将负顾客引进非空竭服务休假且正顾客有流失的M／G／1排队系统，利用求吸收分布以及普通M／G／1排队系统的稳态条件，研究了一类带有负顾客且正顾客有流失的M／G／1非空竭服务休假排队系统的稳态条件。文章利用线性算子的半群理论，讨论该排队系统算子的半群特征，以期进一步研究这些系统解的渐近性，并在此基础上研究系统的可靠性。

1 带负顾客的非空竭服务休假排队模型及模型转换

由文献［13］带有负顾客的非空竭服务休假排队系统的数学模型用以下方程组描述：

其中（t，x）∈［0，∞）×［0，∞）；p0（t）表示在t时刻顾客已结束服务离开系统的概率；p1（t，x）dx表示在t时刻服务器正在为顾客服务，并服务已逝去的时间在［x，x＋dx）之间的概率；p2（t，x）dx表示在t时刻服务器处于工作休假期，并休假已逝去的时间在［x，x＋dx）之间的概率。λ-表示负顾客的到达率；α表示正常状态率；μ（x）表示服务失效率；υ（x）表示休假失效率。

选取状态空间为

显然X是一个Banach空间［14］。下面引进算子及其定义域：

则方程组（1）-（6）可以描述为Banach空间X上的一个抽象Cauchy问题：

引理1 A生成一个C0-半群。

引理2 B是有界算子。

2 带负顾客的非空竭服务休假排队系统算子的半群特征

定理1 A＋B生成一个正压缩C0-半群S（t）。

证明 分两步证明此定理。第一步指出B是有界线性算子，并推出A＋B生成一个C0-半群S（t）。第二步由算子的耗散性和Philips定理得到S（t）是一个正压缩C0-半群。

由B的定义对∀p=（p0，p1，p2）∈X，∀q=（q0，q1，q2）∈X，∀k，l∈R有

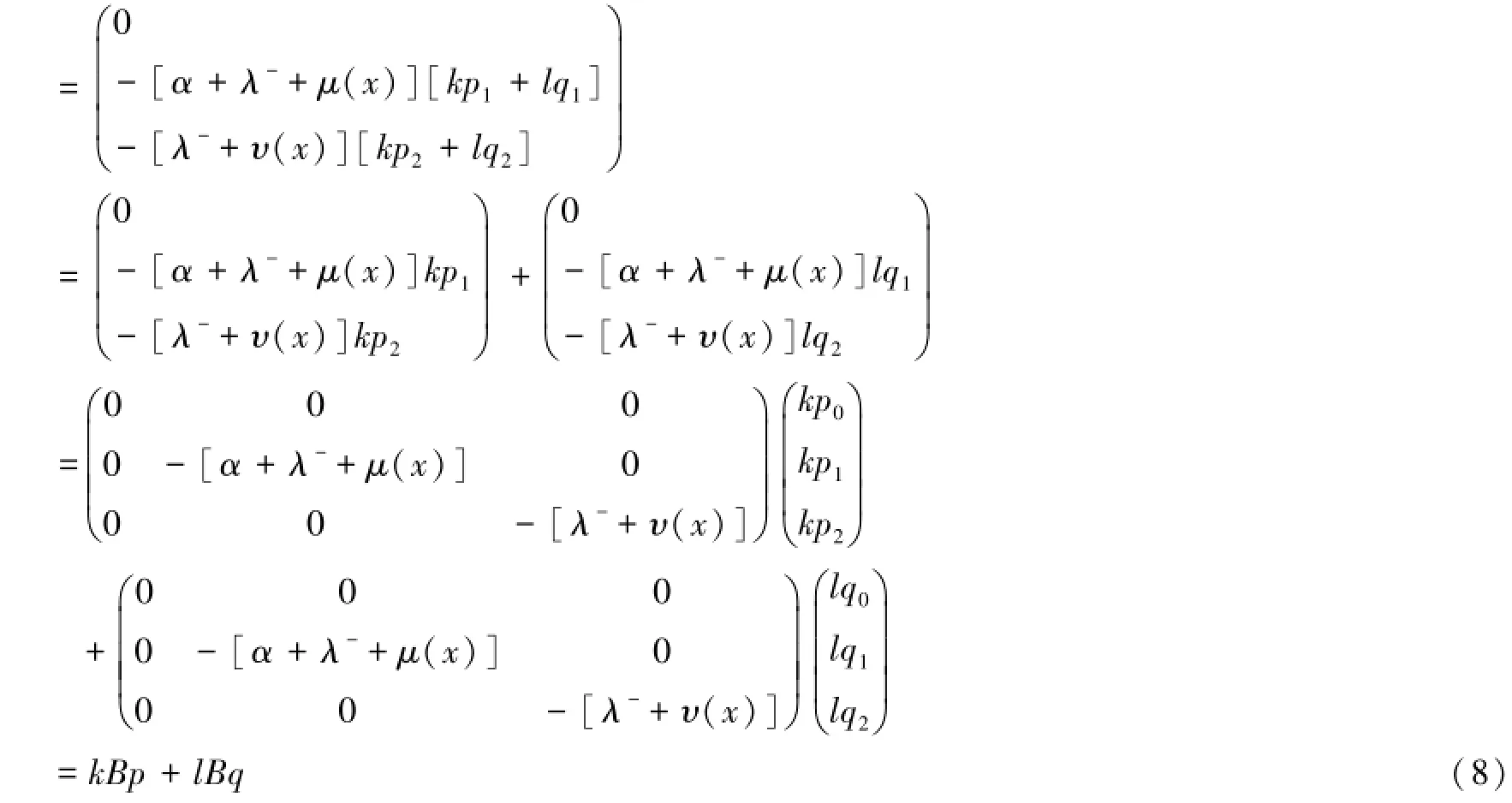
（8）与引理2表明B是有界线性算子。此结果结合到引理1与C0-半群的扰动定理［3］知道A＋B生成一个C0-半群S（t）。

第二步证明A＋B是dispersive算子。对p（x）=（p0，p1（x），p2（x））∈D（A），令

对p∈D（A）与上述的φ（x），由（9）式与边界条件推出

此式说明算子A＋U是dispersive。因此由Philips定理得到A＋U生成一个正压缩C0-半群［3］。再由半群的唯一性理论［3］即知这个正定压缩C0-半群就是S（t）。定理证毕。

此结论对于今后进一步讨论该排队系统算子的拟紧性、豫解集和渐近稳定性等方面发挥着重要的作用。

［1］Pazy A.Semigroups of Linear Operators and Applications to Partial Differential Equations［M］.New York：Springer-Verlag，1983.

［2］Engel KJ.，Nagel R.One-parameter Semigroups for Linear Evolution Equations［M］.Graduate Texts in Mathematics，New York：Springer-Verlag，2000.

［3］Gupur G.，Li X Z，Zhu G T.Functional Analysis Method in Queueing Theory［M］.Hertfordshire：Research Information Ltd，2001.

［4］Alim Mijit，Geni Gupur.Asymptotic behavior of the time-dependent solution of the M／M／1 queueing model with optional second service［J］.Inter⁃national Journal of Pure and Applied Mathematics，2011，69：289-328.

［5］阿力木·米吉提.第二种服务可选的M／M／1排队模型的一个注［J］.新疆大学学报（自然科学版），2012，29（4）：414-420.

［6］Alim Mijit.Semigroup method on a MX／G／1 queueing model［J］.Advances in Mathematical Physics，2013：893254.

［7］Alim Mijit，Geni Gupur.Semigroup approach of a two-unit system with connecting and disconnecting effect［J］.International Journal of Applied mathematics and Statictics，2013，41：23-30.

［8］阿力米·米吉提.一类排队模型的适定性［J］.安徽师范大学学报（自然科学版），2013，36（2）：110-114.

［9］阿力木·米吉提，蔡玲霞.一个排队模型时间依赖解的渐近性质［J］新疆师范大学学报（自然科学版），2014，33（2）：53-57.

［10］阿力米·米吉提.带负顾客的非空竭服务休假排队模型非负解的存在唯一性［J］.江西师范大学学报（自然科学版），2014，38（6）：574-577.

［11］Alim Mijit.Time-dependent analysis for a two-unit system with connecting and disconnecting effect［J］.Gazi University Journal of Science，2015，28（1）：27-35.

［12］阿力米·米吉提.一类由两个同型部件与一个修理设备构成的系统研究中出现的投影算子的表达式［J］.新疆大学学报（自然科学版），2015，32（1）：45-56.

［13］尹小玲.带负顾客的非空竭服务休假排队系统的稳态分析［J］.中山大学学报（自然科学版），2008，47（2）：1-4.

［14］阿力木·米吉提，蔡玲霞.第二种服务可选的M／M／1排队模型状态空间及对偶空间的完备性［J］.新疆师范大学学报（自然科学版），2012，31（2）：72-76.

Semigroup Characteristics of a Queueing System Operator with Negative Customers

Oghuljan·AINI
（No．2 Middle School of Urumqi，Urumqi，Xinjiang，830000，China）

By using the strong continuous semigroup theory of linear operators in functional analysis，we dis⁃cuss the semigroup characteristics of the system operator expressed by the queue with negative customers and vaca⁃tion on non-exhaustive service.Our results show that the underlying operator of the model generates a positive con⁃traction C0-semigroup S（t）.

Queue system with Negative Customers；abstract Cauchy problem；linear operator；dispersive op⁃erator

G623.5

A

1008⁃9659（2015）03⁃056⁃04

2015-06-10

新疆广播电视大学基金（2013xjddkt001）。

奥古丽江·艾尼（1977-），女，新疆吐鲁番人，中教一级，主要从事中学数学教学和模型的动态分析方面的研究。