可测集的结构及其应用

玛哈提·胡斯曼

（新疆师范大学数学科学学院，新疆乌鲁木齐830054）

可测集的结构及其应用

玛哈提·胡斯曼

（新疆师范大学数学科学学院，新疆乌鲁木齐830054）

实变函数论是微积分的进步，其目的是想克服黎曼所建立微积分学存在的缺点，使得微积分的运算更对称更完美。可测集是实变函数中基本而重要的概念之一。内外测度相等的有界点集E称为勒贝格可测集（简称可测集）。文章讨论可测集定义的等价性，性质以及可测集与开集，闭集的关系，用开集、闭集，刻画出开集可以从外部逼近，可测集、闭集可以从内部逼近。

可测集；开集；闭集

实变函数论中心问题是建立勒贝格积分理论。数学分析中考虑函数f（x）在区间［a，b］上黎曼积分时，对区间进行分划T并作积分和数，f（ξi）△xi即当分划的细度｜｜T｜｜→0时，积分和数的极限存在且与分化的方法及介点ξi的取法无关，就必须要求函数f在这些小区间上的函数值变动不大。这表明黎曼可积函数类太窄，加之黎曼积分存在缺陷。

若交换积分与极限运算的条件太苛刻，可积函数类的充要条件没有解决，从而求原函数的问题得不到彻底解决。近代物理与概率论的发展要求改造黎曼积分，引进应用更灵活的新积分。考虑不是分划函数f（x）的定义域，而且对函数的值域R（f）=f（［a，b］）做某种分划［2］，这样便能保证函数在每个［yi-1，yi］上值的变化不大，记作Εi=［x：x∈［a，b］，yi-1≤f（x）＜yi］则Εi不一定是区间。则需要通过对Εi进行某种度量，即必须推广区间长度概念，对一般的点集建立一种合理的度量，即推广长度概念，又必须保留长度概念的基本性质，这就是集合的测度。

1 零测度集（简称零集）

零测度集的概念与黎曼积分的局限性有关。定义在［a，b］上的非负函数f（x），如果可积，则其积分值应为曲线y=f（x）的下方图形的面积。对于狄利克雷函数D（x）是勒贝格积分下可积函数，该面积可理解为一有理数集为底，高为1的“矩形”的面积，此值就应为［0，1］∩Q的“长度”。在黎曼积分中这种非区间数集的“长度”是没有意义.再说我们把区间长度的概念推广到一般的集合。设I=［a，b］为区间，定义I的长度为m（I）=b-a，对单点集a{}有m（a）=m（［a，a］）=0，故单点集的度量（测度）为零或零测度集由于有限点集是有限个单点集之并集，即任何有限点集也是零测度集。

一般地，如果能把一个集合分解为有限个互不相交的区间之并，则该集合的长度应该等于这几个区间的长度之和，如果不能把给定的集合分解为一些区间之并集时，考虑覆盖该集合的区间系。我们考虑由可数个区间构成的覆盖，从这点出发可给出如下“零测度集”定义。

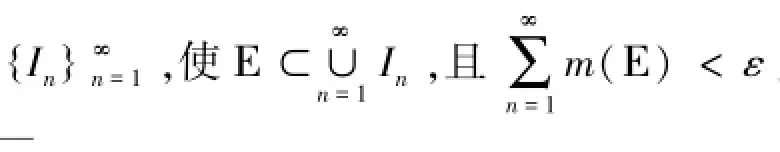
2 有界集的测度

开集与闭集的测度：利用区间的长度以及开集的构造定理引进开集的测度概念。

定义2 设G是非空开集G=∪i（αi，βi），（αi，βi）为G的构成区间，

设F为非空有界闭集，令α=inf｛x：x∈F｝，β=sup｛x：x∈F｝，

因此G0=［α，β］-F，G=（a，b）-F是开集，从而有b-a-m（G）=β-α-m（G0）

这表明b-a-m（G）只与F有关，而与区间（a，b）的选择无关。

定义3 设F为非空有界闭集，任取包含F的开区间（a，b），令G=（a，b）-F，则G为开集，定义b-a -m（G）为闭集F的测度。

性质1 设F为有界闭集，G是有界开集且F⊂G，则m（G-F）=mG-mF［4］。

定义4 设Ε是有界集，定义m∗Ε=inf｛mG：G⊃Ε，G是开集｝为外测度

m∗Ε=sup｛mF：Ε⊃F，F是闭集｝为内测度。

定义5 设E是有界集，如果m∗Ε=m∗Ε，则称Ε是勒贝格可测集。

3 勒贝格外测度

零集的概念为我们建立一般集合的“长度”概念提供了思路。

设Ε为Rn中任意集合，为定义Ε的“长度”，使用从Ε的外部包围Ε的方法。

用一列区间构成的区间系去覆盖Ε，这一列区间的长度之和为该覆盖的总长度。

由于ZΕ是以0为下界的非空集合，故它的下确界是存在的。对Rn中的任何集Ε，都有外测度，对有些集Ε，级数m（In）可能对任何覆盖都发散，因此m∗Ε可以为∞。

当m∗Ε＜＋∞时，对∀ε＞0，必存在一列开区间｛In｝，满足In⊃Ε且In｜＜m∗Ε＋ε。

勒贝格外测度除具有单调性以外还有次可加性和平移不变性。

勒贝格建立的外测度是定义在Rn的一切子集构成的集合类P（R）上的集函数，它是区间长度概念推广的，尽管它有许多好性质并具有次可加性，即集合的外测度一般不满足可列可加性，这表明外测度m∗（·）不能作为长度概念在P（R）上的延伸。希望去掉P（R）中分出一个子集族，使m∗（·）在其上具有可列可加性，这子集族包含足够广泛的集合。

4 勒贝格可测集与勒贝格测度

在外测度的基础上，在Rn中诱导出集族Ω，使在其上m∗（·）除满足外测度的性质外还是可列可加性的。在概率论中，用Α∩Ε，Α∩Εc的概率之和表示事件Α的概率，而对集合Α，Ε来说m∗Α=m∗（Α∩Ε）＋m∗（Α∩Εc）不一定成立，如果Ε是勒贝格可测集必有等号成立，反之亦然，即可测集的充要条件是等号成立［3］。

定义7 设Ε⊂Rn，如果对任一集T⊆Rn，有m∗T=m∗（T∩Ε）＋m∗（T∩Εc），则称Ε为勒贝格可测集，即m∗Ε=mΕ为集合Ε的勒贝格测度。

5 主要结果

定理1 若Ε⊂Rn有界可测集满足m∗Ε=m∗Ε，则对∀Α⊆I有m∗A=m∗（Α∩Ε）＋m∗（Α∩Εc）。

证明 由Α=（Α∩Ε）∪（Α∩Εc）得，m∗Α≤m∗（Α∩Ε）＋m∗（Α∩Εc）（1）

反之，由于m∗Α=inf｛mG｜Α⊆G，G为开集｝。故由下确界定义，有开集G，Α⊆G⊆I，使得mG＜m∗Α＋ε。而G可测集，所以Gc也可测集。

由于Ε∩G⊆G，Εc∩G⊆Gc，故

有内测度定义知｜I｜=m∗Ε＋m∗（I-Ε），但是

故（1）和（2）知定理1证毕。

定理2 若mΕ＜∞，则定义5和定义7等价，即

（1）m∗Ε=m∗Ε

（2）对∀T⊆Rn，m∗T=m∗（T∩Ε）＋m∗（T∩Εc）

证明 先证（2）⇒（1）设对∀T⊆Rn，m∗T=m∗（T∩Ε）＋m∗（T∩Εc）

取T为开区间I且使Ε⊆I，有｜I｜=m∗（I∩Ε）＋m∗（I∩Εc）=m∗Ε＋m∗（I-Ε）

从而有m∗Ε=｜I｜-m∗（I-Ε）=m∗Ε

再证（1）⇒（2）。因Ε是有界集，可取开区间I⊇Ε，则Ε∩Ic=∅

而由定理1，且T∩I⊂I可得m∗（T∩I）=m∗（T∩I∩Ε）＋m∗（T∩I∩Εc）

故，由I的可测性，将上述二式相加，得m∗T=m∗（T∩I）＋m∗（T∩Ic）≥m∗（T∩Ε）＋m∗（T∩Εc）

另外，对任意集T，有m∗T≤m∗（T∩Ε）＋m∗（T∩Εc），即Ε为可测集

6 可测集的结构

勒贝格可测集的结构虽不像波雷尔集那样形象和容易把握，但通过以下的逼近定理可予以刻划。

定理3［4］（逼近定理）设Ε⊂Rn有界集，则

（1）设Ε可测⇔对∀ε＞0，存在开集G与闭集F，使得F⊂Ε⊂G，且m（G-Ε）＜ε，m（Ε-F）＜ε。

（2）Ε可测⇔对∀ε＞0，存在Gδ型集G与Fσ型集F，使得F⊂Ε⊂G且m（G-F）=0。

定理4［2］设Ε⊂Rn可测的充要条件是：对∀ε＞0，存在开集Ε⊂G1，Εc⊂G2，使得m（G1∩G2）＜ε。

这个逼近定理表明，可测集可以用包含它的开集或含于其内的闭集去任意逼近，而且任何勒贝格可测集与Gδ型或Fσ型集合相比，仅仅相差一个零测度集。即用全体Gδ型集或Fσ型集合全体零测度集，可以构造勒贝格可测集。

全体勒贝格可测集的集合L（R）是R的幂集P（R）的真子集，这表明一定存在勒贝格不可测集。

［1］程其襄，等.实变函数与泛函分析基础［M］.北京：高等教育出版社，2010：56-69.

［2］周民强.实变函数论［M］.北京：北京大学出版社.

［3］赵静辉.实变函数简明教程［M］.华中理工大学出版社，1996：56-60，72-83.

［4］江泽坚，等.实变函数［M］.北京：高等教育出版社，1994：62-76.

［5］赵荣侠，等.测度与积分［M］.西安电子科技大学出版社，2002：31-48.

［6］吴炯新，周戈.实变与泛涵—基本原理与思想方法［M］.厦门：厦门大学出版社，2004.

［7］吴通新，吴卓人，等.实变函数与泛函分析（上）［M］.北京：人民教育出版社，1987.

Discuss the Measurable Set Shallowly the Structure

Mahat·HUSUMAN
（School of Mathematial Scinces，Xinjiang Normal University，Urumqi，Xinjiang，830054，China）

The theory of variable function is the department of infinitesimal calculus，.which makes operation more perfect symmetry of infinitesimal calculus.The purpose of the theory is to overcome the faults of infinitesimal calculus that Riemann established.The measurable set is one of basic and important concepts of variable function. The bounded point set E known as the Lebesgue measurable set（i.e.measurable set）.The present paper discusses the equivalency and the nature of the definition of measurable set.On the other hand，the relationship of the open set and the closed set is also discussed，further more，the paper portrays that open set approach the measurable set from exterior，the closed set may approach the measurable set from the interior.

Measurable set；Open set；Closed set

O174

A

1008⁃9659（2015）03⁃052⁃04

2015-04-29

玛哈提·胡斯曼（1959-），男，新疆阿勒泰人，副教授，主要从事函数论方向的研究。