高维量子纠缠态作为量子信道的热点分析

居 婧， 王先明

（新疆师范大学物理与电子工程学院，新疆乌鲁木齐830054）

高维量子纠缠态作为量子信道的热点分析

居 婧， 王先明∗

（新疆师范大学物理与电子工程学院，新疆乌鲁木齐830054）

文章分析了量子隐形传态当前的热点内容，并以四维纠缠态作为量子信道传送未知粒子提出两种方案，在分析两种方案中可以看出如果Alice测量结果和Bob的幺正操作是合适的，未知粒子态就会以最大概率传送。

量子通信；量子隐形传态；高维纠缠态

量子信息学作为一门交叉科学，在物理、通信、军事、国防和计算机计算中都有广泛的研究与应用，涉及领域广泛，而它的主要的研究内容是量子计算和量子通信。而量子隐形传态研究又是量子通信中的重要热点之一，同时也是量子信息学的基础研究［1-2］。

自Bennett等人首次提出量子隐形传态方案以来，量子隐形传态在理论上得到迅速发展，不止如此，量子隐形传态在实验上也早已应用。在理论上，1994年Vaidmand Ld等人提出连续变量的量子隐形传态方案，1997年郑仕标、郭光灿等人提出QED的量子隐形传态方案，1998年Braunstein等人提出通过用双模压缩的真空场进行了连续的相干光场的隐形传态，2003年Roa L等人提出D维量子系统的量子隐形传态方案［4-14］。

从实验上来看，1997年由奥地利的科学家首次验证了在室内的量子隐形传输，随后在2004年，实现了600米的量子隐形传输，到2012年，中国和奥地利的科学家都完成了百公里的量子隐形传输［15］。

随着量子隐形传态理论和实验的发展，时代赋予了量子隐形传态更加重要的使命，使得其在今日依旧是一个热点，文章则是以四维纠缠态作为量子信道传送未知粒子提出两种方案，在方案中使用了对称测量、非对称测量和适当的局域幺正变化操作。

1 两种方案

假设Alice和Bob分享的四维纠缠信道为

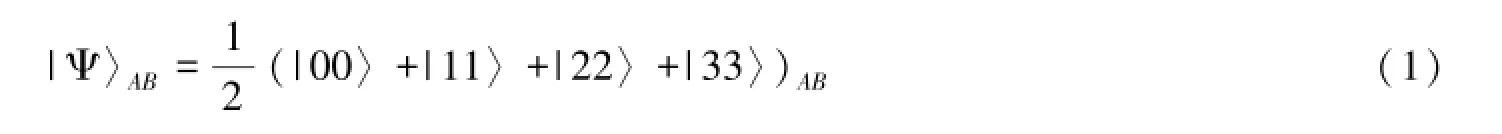
如果Alice想要传送一个未知粒子

那么可以把整个系统写成

为了实现未知粒子的传输，Alice对粒子A和a进行测量。

方案一：

如果Alice的测量基是

不失一般性，如果Alice的测量基是｜φ11〉aA，那么B粒子将会坍塌成

因此Bob不需要做任何的操作就可以得到未知粒子，成功的实现粒子的传输。

此时，Bob则需要根据Alice公布出来的测量结果对（6）式执行幺正操作

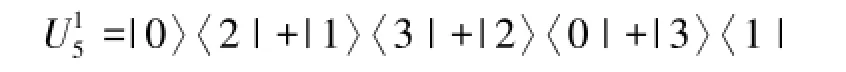
这样就可以得到未知态，实现量子态的重现。

相似地，Bob将会执行以下幺正操作，实现未知粒子的传输：

方案二：

如果Alice的测量基是

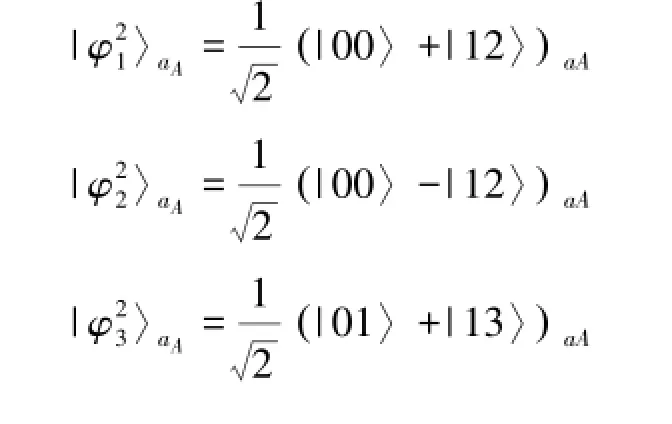
每个测量基都会导致粒子B的坍塌，而每个测量基对应的B粒子的坍塌态如下：

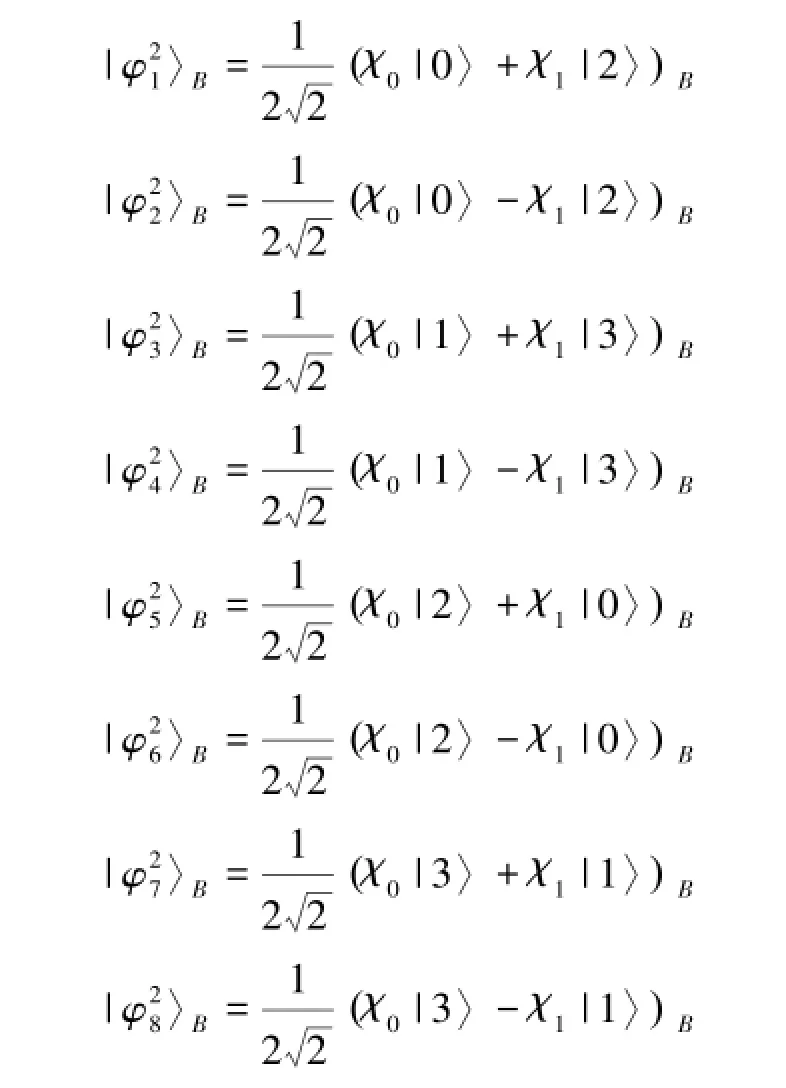
随后Bob将会根据以上结果，做对应的幺正操作，如下：

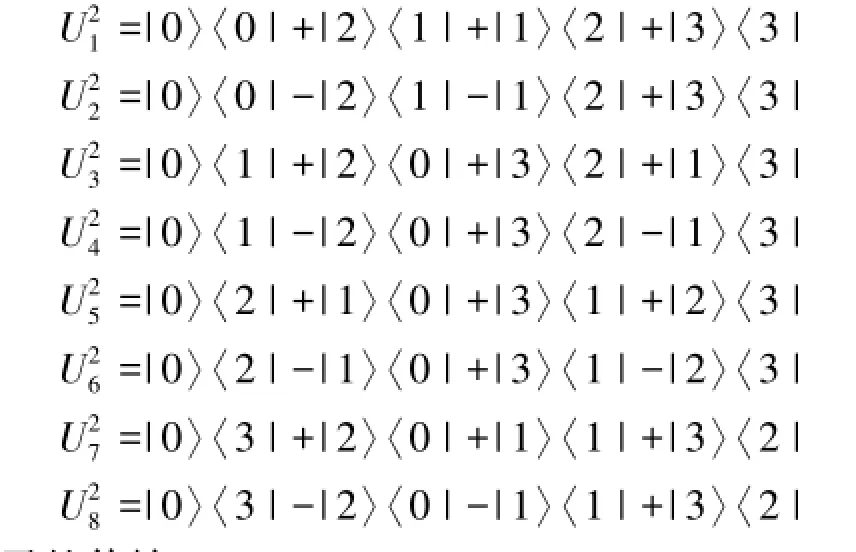
这样就会成功实现未知粒子的传输。

2 结果与讨论

文章分析了量子隐形传态当前的热点内容，并以四维纠缠态作为量子信道传送未知粒子提出两种方案，在分析根据以上两种方案中，看出如果Alice测量结果和Bob的幺正操作是合适的，未知粒子状态就会以最大概率传送。

参考文献：

［1］张婷.三粒子任意态的量子隐形传态的理论研究［D］.新疆：新疆师范大学，2013.

［2］李刚.量子隐形传态与量子信道［D］.福建：福建师范大学，2012.

［3］赵文卓.量子通信—量子信息时代到来的前奏［J］.物理前沿，2014，26（7）：46-50.

［4］叶欣露.高维量子纠缠态的制备及其在量子通信中的应用［D］.厦门：华侨大学，2013.

［5］C H Bennett，G Brassard，C Crepeau，et al.Teleportation an unkown quantum state via dual classical and EPR channel［J］.Phy Rev Lett，1993，70（13）：1895-1899.

［6］李翠翠.基于六粒子态的量子隐形传态与量子密集编码［D］.江西：江西师范大学，2013.

［7］张伶伶.基于多维多粒子量子信道的量子安全直接通信［D］.苏州：苏州大学，2009.

［8］S L Braunstein，H J Kimble.Teleportation of contonuous quantum variable［J］.Phys.Rev.Lett，1998，80（4）：869-872.

［9］L.Vaidman，teleportation of quantum states［J］.Phys.Rev.A，1994，49：4394.

［10］S.B.Zheng，G C Guo，Teleportation of an unknown atomic state throug the Raman atom-cavity-field interaction［J］.Phys.Lett.A，1997，232（3-4）：171-174.

［11］S.B.Zheng，G C GUO，Teleportation of acroscopic states of a cavity field［J］.Phys.Lett.A，1997，236（3）：180-182.

［12］L.Roa，A.Delgado，I.Fuentes-Guridi，Optimal conclusive teleportation of quantum states［J］.Phys.Rev.A，2003，68：022310.

［13］詹孝贵.高维Hilbert空间中量子隐形传态的研究［D］.山东：山东师范大学，2007.

［14］徐兵杰，刘文林，等.量子通信技术发展现状及面临的问题研究［J］.通信技术，2014，5（47）：463-468.

［15］张树怀.量子通信技术的发展趋势［J］.科学向导，2015，2：191.

Analysis of Hot Sports on High Dimensional Quantum Entangled States as Quantum Channel

JU Jing， WANG Xian-ming∗
（College of Physics and Electronic Engineering，Xinjiang Normal University，Urumqi，Xinjiang，830054，China）

The hot content of quantum teleportation is analyzed，and two schemes are proposed to transmit an unknown single-qubit state by using 4-dimensional entangled state as the quantum channel.In the analysis，the two schemes can be seen if the Alice’s measurement and the unitary operation of Bob are appropriate，the teleportation can be successfully realized with the maximal probability.

Uantum communication；Quantum teleportation；High-dimensional entangled state

0431

A

1008⁃9659（2015）03⁃048⁃04

2015-08-29

居 婧（1990-），女，新疆哈密人，硕士研究生，主要从事量子通信的研究。

∗［通讯作者］王先明（1958-），男，湖南衡山人，教授，硕士生导师，主要从事量子通信的研究。