考虑学习效应的重复性建设项目最低成本问题
2015-05-25张立辉熊俊德格吉日夫
张立辉,熊俊,德格吉日夫
(华北电力大学经济与管理学院,北京 102206)
考虑学习效应的重复性建设项目最低成本问题
张立辉,熊俊,德格吉日夫
(华北电力大学经济与管理学院,北京 102206)
在重复性建设项目过程中,学习效应是一种很常见的现象。但目前还没有研究将学习效应应用到重复性项目的工期与成本优化问题中。本文将学习效应考虑到重复性项目最低成本问题中,分析了学习效应对项目成本的影响,建立了考虑学习效应的项目总成本模型,并设计了一种改进的粒子群算法进行求解。算例表明,学习效应有助于缩短项目工期、节约成本。本文研究有利于项目计划人员充分利用学习效应制定更为合理的进度方案。
学习效应;重复性项目;最低成本问题
重复性建设项目是指在建设工程的每个单元各个工序不断重复进行的项目,如高速公路、管道工程、铁道工程、隧道工程、高层建筑等。目前国际上关于重复性项目调度的研究基本上可以归为两类,一是关于重复性项目调度的基本理论研究,如关于确定控制路线(Controlling Path)[1~3]、关键性分析[4,5]等;二是关于重复性项目调度中的各种实际问题,如时间-费用权衡[6,7]、资源均衡[8,9]等的研究。当前我国处于基本建设大发展时期,大量的重复性建设项目如高速公路、铁路、地铁、管道工程等正在兴建或规划中,这些项目投资大、工期长,因此重复性项目调度研究具有很实际的意义。
本文所研究的最低成本问题是指在给定工期范围内找出所有可行方案中的最低成本方案,属于离散时间-费用权衡(discrete time-cost tradeoff problem,DTCTP)问题的一种[10]。离散时间-费用权衡是项目调度中的一种双目标优化问题,属于强NP难问题。DTCTP的解决方法主要有基于动态规划[11]和分支定界的精确算法[12],也有基于启发式规则的各种启发式算法[13]以及智能算法[14,15]。目前对该问题的研究大都采用智能算法求解,如Hyari等构建了能权衡总工期与总费用的遗传算法,并采用Pareto最优性原理对重复性建设项目的调度方案优化[7];Zhang等用遗传算法解决了考虑软逻辑下重复性项目的时间费用权衡问题[14];Long等设计了考虑工序优先关系和工作连续性的遗传算法,并将其应用于优化重复性项目的工期和费用[15]。但是,以上研究都没有考虑学习效应对项目的影响。
学习效应是指随着以人工为基础的工作经验不断累积,工人的工作效率会逐渐提高的现象。在重复性建设项目中,相同或相似的工作在多个单元中不断重复,恰恰是学习效应最常发生的领域。实际上,1936年W right提出学习曲线原则[16]后,建筑领域就开始逐渐认识到学习现象的普遍存在并开始将其影响考虑到实际的项目问题中。Arditi等发现随着完成单元的增加,学习现象将会越来越明显,并且用LOB描绘了学习效应引起生产率的变化情况[17]。Couto等验证了学习效应在建筑领域预测方面的应用性和有效性。他认为学习效应的发生需要一些外界条件保证,但是没有总结影响学习效应的因素[18]。Pellegrino等实例分析了在意大利多层混凝土建筑中影响学习效应的因素,他认为采取适当的措施如增强现场管理、采取适当的激励机制和其他管理手段将会有效提高学习效应[19]。
本文将学习效应考虑到重复性建设项目的最低成本问题中,并提出一种优化的PSO算法解决该问题。通过对计算结果的比较分析,讨论学习效应对项目工期、成本以及最优调度方案的影响。同时考虑了为了维持学习效应而需要额外支出的管理成本。
1 学习效应及其对项目成本的影响
1.1 学习效应的直线模型介绍
1936年,Wright在观察飞机制造厂生产过程中提出了学习曲线的概念[16]。他发现随着产量的增加,生产一个产品的时间也会按百分比降低。这个百分比就是学习率。学习曲线是研究工人生产过程中生产率变化的工具,能直观反映学习率的变化过程[20]。随着学习曲线的提出,各种学习曲线模型也相继出现,其中应用最广泛的有:直线模型[20]、斯坦福-B模型[21]、指数模型[22]、S型曲线模型[23]等。下面具体介绍直线模型。
直线模型,即对数线性模型。以对数-对数形式绘图时,图形表现为直线。基本特征是工序在开始到结束时间内学习率保持恒定。数学表达式如下:

式中:j表示累积工作单元数;y表示工序j个单元的累积平均单元工作时间;A是常数,其值等于完全没有经验的工人完成第一单元的工作时间;n (n<0)表示学习指数,S表示学习率(%),式(2)定量表示了两者的关系;Tj表示第j个单元的工作时间。
Moselhi等提出了一种基于位置的学习曲线模型[24],它类似于直线模型。数学表达式如下:

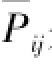
本文实例选取直线模型作为学习曲线模型。Blancett认为,直线模型能够广泛应用于重复性项目中预测生产率的学习曲线模型[20]。Everett和Farghal发现,直线模型能够可靠地预测学习效应对建筑领域的影响[22]。
1.2 重复性建设项目中学习效应对成本的影响
学习效应对生产率的影响是由学习率来衡量的。学习率的确定有助于定量分析学习效应对项目的影响。欧洲建筑领域的一项统计数据表明,建筑领域的学习率大约是90%;联合国的一项研究数据表明,建筑领域的学习率一般在80~95%之间[17]。学习率的高低受多种因素影响,有些因素是不可控或由项目本身决定,如天气条件、工作类型(复杂性和重复程度)等,有些因素则是可控的,包括项目计划与设计质量、现场管理、雇佣工人的项目经验和对工人的培训以及激励措施等[17,18]。更多关于重复性建设项目中影响学习效应的因素请参阅文献[18]、[19]。
学习效应从两方面影响重复性项目的成本。一方面,在重复性项目中,通过利用学习效应,可以使工人工作效率提高,从而缩短项目总工期,由此可能降低直接成本中与总工期有关的部分(如计时工资、设备租赁费用等),同时也可能降低项目的间接成本(如按照工期计算的管理费用)。此外,由于工程提前完工,还有可能获得业主的奖励。但是另一方面,为了获得更好的学习效应,需要为此支付额外的成本,例如,为了雇佣经验丰富的工人可能要支付更高的工资,对工人培训、加强现场管理、提高激励水平等措施都会导致管理费用的增加。因此,项目管理人员需要进行权衡,优化调度方案。
2 考虑学习效应后项目成本问题的描述和模型
2.1 项目成本问题的基本描述
具有学习效应的重复性项目问题描述如下:设有N个工序,每个工序有相同的单元数M。工序i(i=1,2,…,N)有bi种执行模式,执行模式用Mik(k=1,2,…,bi)表示。一种执行模式对应一种学习率Lik。通过式(5)计算工序i第j单元的工期。

式中:珔dijk表示不考虑学习效应的影响下选择执行模式Mik时工序i第j单元的工期;Qji表示工序i第j单元的工作量。Pijk表示在执行模式Mik,学习率Lik下单元j的生产率。
通过式(6)计算考虑学习效应后工序i第j单元的工期。式(6)采用Moselhi等提出的基于位置的直线模型[21]。

式中:dijk表示在考虑选择执行模式Mik,学习率Lik情况下工序i第j单元的工期;i=1,…,N;j=1,…,M;k≥1。
项目的总成本由以下部分组成:直接费用(DC),间接费用(IC),延迟处罚(OC)或提前奖励(AC),和租赁费用(RC)。考虑到为了维持学习效应而增加的成本,增加一个额外的学习费用(LC)。各部分成本具体计算如下:
通过式(7)计算项目直接费用(DC),由项目中每个工序各单元的材料费用(MC)、劳动力费用(WC)、设备费用(EC)之和构成。
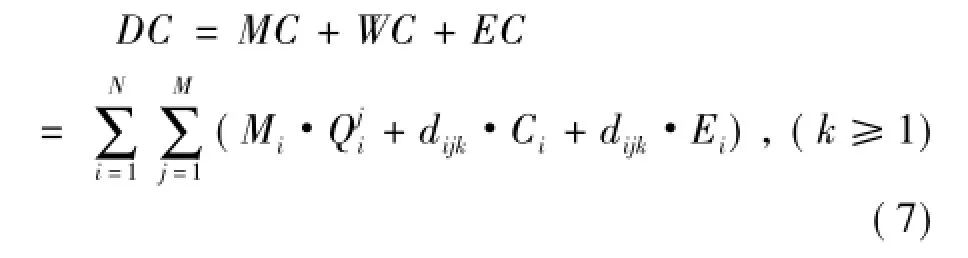
式中:Mi表示工序i的单位材料费用;Qji表示工序i的单元j完成所需的材料数量;劳动力费用为Ci/d;设备费用为Ei/d。
通过式(8)计算项目间接费用(IC),由项目中每天对应的费用之和构成。

式中:ICRd表示第d天的间接费用;D为项目的总工期。
通过式(9)计算延迟处罚费用(OC)或提前奖励(AC)。

式中:SD表示项目限定时间即项目规定的奖励惩处分界点;ORt表示项目实际完成比项目限定时间多的天数每天需要缴纳的延迟惩罚费用。式(10)表示设备的租赁费用(RC)。
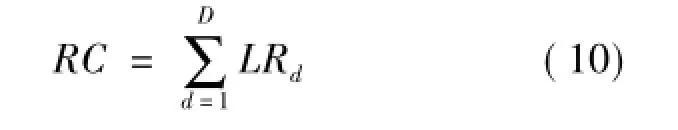
式中:LRd表示第d天的设备租赁费用。
通过式(11)计算项目维持学习效应的学习费用(LC),由项目中各工序的各个单元对应的费用之和构成。

式中:NCik表示在工序i上执行模式为Mik,学习率为Lik时,维持学习效应的学习费用。该项费用与工序所选的执行模式、学习率有关。
测试方法:以4个标记构成测试路线,4个标杆形成十字,直线距离为5m,十字的中点位置放置标记作为信号接收的起点和信号应答完毕后的终点。受试者站立于中点位置,根据随机信号指令完成4个不同方向的触杆动作。在该项指标测试中,受试者需完成的触杆次数为4次,跑动距离为10m,不仅能够反映出受试者视觉信号的搜索能力、信号的应答速度,也能够体现出受试者在完成动作时肢体的协调配合、动作的高效组织能力。指标测试以速度为核心,计算受试者根据信号指示准确完成相应的应答动作的时间。
2.2 总成本数学模型
(1)目标函数
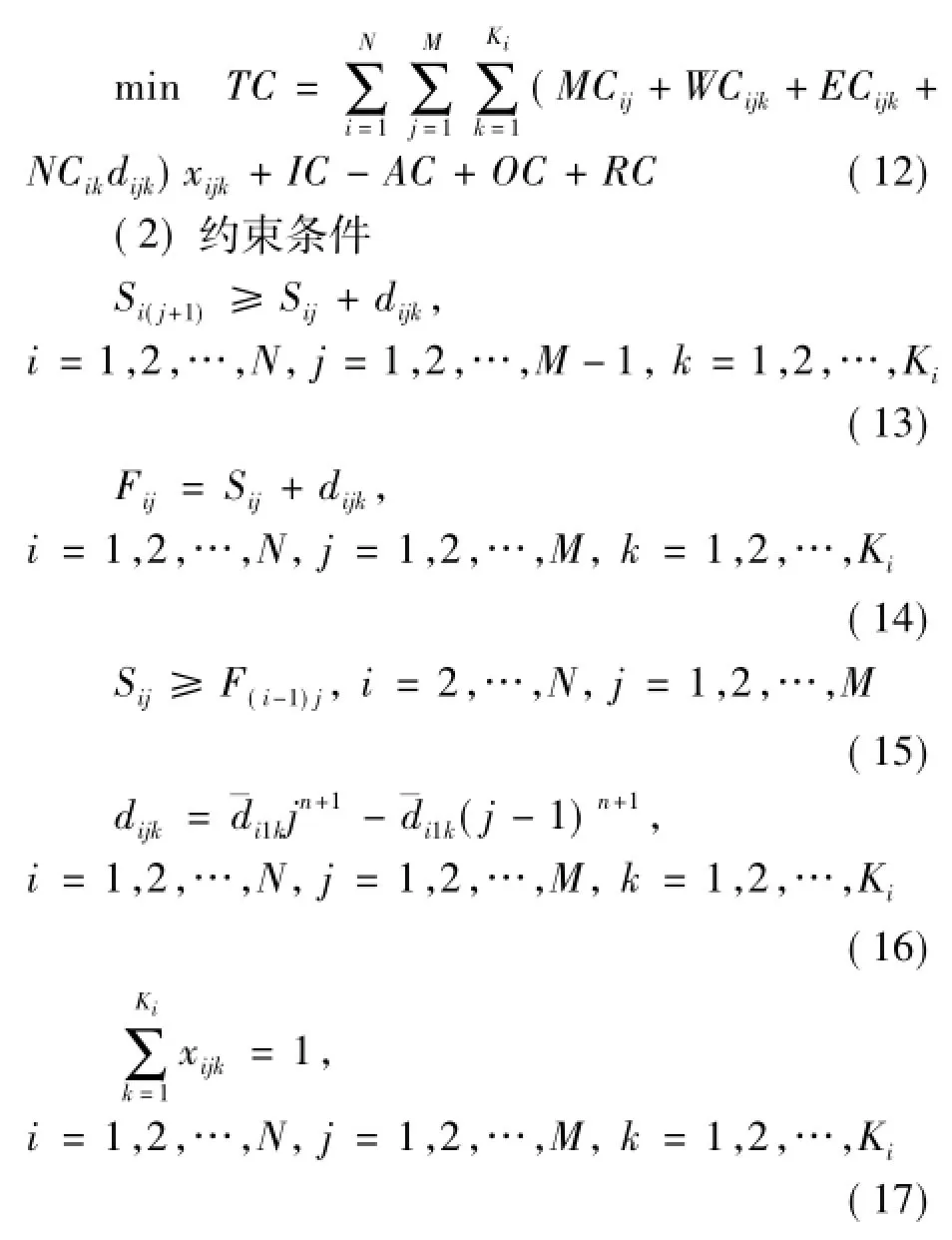

式中:i为工序数;j为单元数;N为工序总数;M为单元总数;bi为工序i的可选执行模式数;目标函数(12)最小化项目总成本,xijk是二进制数(如果子工序aij在模式k下执行,xijk取1,否则,xijk取0);约束(13)表示在同一工序aij中子工序完成后子工序ai(j+1)才可能开始;Sij表明子工序aij的开始时间;约束(14)计算子工序aij的完成时间;约束(15)表明子工序应该满足结束开始优先关系;约束(16)dijk表示工序i的学习率为Lik时,子工序aij的工期;约束(17)表示每个子工序有且仅有一种执行模式可被选择,同一工序内任意两种执行模式不能同时执行;约束(18)要求项目的工期不能超过给定的最大工期限制Tmax。
3 改进粒子群算法求解
由于所需解决的问题在实际项目中是一个NP-问题,用精确算法计算运行时间过长且难以得到满意解。粒子群优化算法是通过群体中粒子的相互影响而产生的并行搜索算法[25],能用来解决传统搜索方法无法解决的目标函数非线性问题。
3.1 粒子信息
求最小成本问题时,粒子中有两类变量:(1)各个工序的执行模式;(2)各个工序的学习率,如图1所示。本文将执行模式确定到每个重复单元,Mik表示工序i选择了第K种执行模式,Lik表示工序i执行模式K对应的学习率。

图1 一个粒子的结构
3.2 进化规则及步骤
首先,必须将当前代种群粒子中各个工序的工期和总工期计算出来;然后,通过结果比较得出最小成本的粒子;最后,通过该粒子的速度和位置与种群中粒子的速度和位置计算得到下一代;重复之前的步骤直到得到近似最优解或达到设定的迭代次数,得到种群最优方案的进化规则如下。
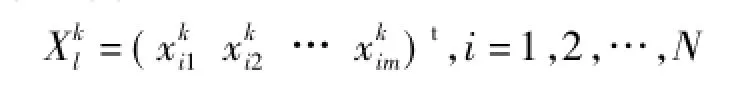
式中:N为工序的总数。
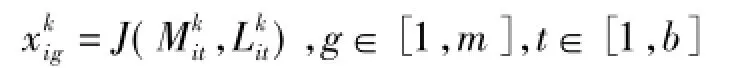
式中:b表示工序i可选执行模式数,每一维记录了执行模式M和学习率L的选择。
(2)定义适应函数即为目标函数:
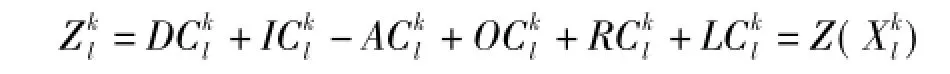
(3)获得当前最优粒子和全局最优粒子:
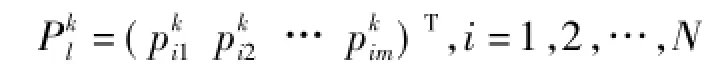
上式为第l个粒子当前代中得到的最优粒子;
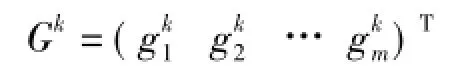
上式为从初始代到当前代的全局最优粒子;
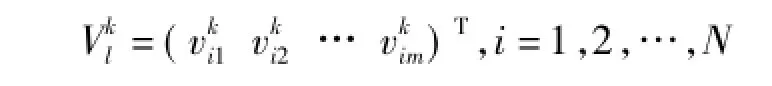
上式为第l个粒子的位移速度。
(4)更新第i个粒子速度和位置:

下面具体说明算法实现步骤:
步骤1:选定算法的参数。确定初始种群并计算出初始位移和速度。
步骤2:计算每个粒子的适应度。分别更新每个粒子的个体极值Pi和累积所有代的全局最优方案。
步骤3:更新种群粒子的信息。由于项目的执行模式和学习效应的非连续性,将按下式对得到的新种群粒子进行校正,保证执行模式在给定范围内。

步骤4:判断是否达到预定的迭代次数。此处未设置工期延迟的惩罚函数,因为奖惩费用已经计算在内。
步骤5:若成立,则停止计算,输出结果。若不成立,令k=k+1并转到步骤2。
4 计算实例
本文采用一个三跨混凝土桥建设项目作为算例。该项目由五个工序构成,分别是挖涵洞,填地基,立桥墩,上大梁和铺桥面。项目合同工期为115天,若工期超过115天,超过部分每天赔偿5000美元;若项目提前完工,则每提前一天奖励8000美元。项目管理费用(不包括学习效应维持费用)为2500/天。项目其它基本信息如表1所示。根据2.2节阐述并结合具体的经验数据给出各工序可获得的学习率及为了维持该学习率所需的学习费用,如表1所示。学习率主要是根据各工序的不同特点以及工序的工作复杂度确定,学习费用主要是管理者施加激励机制以及相关管理措施产生。
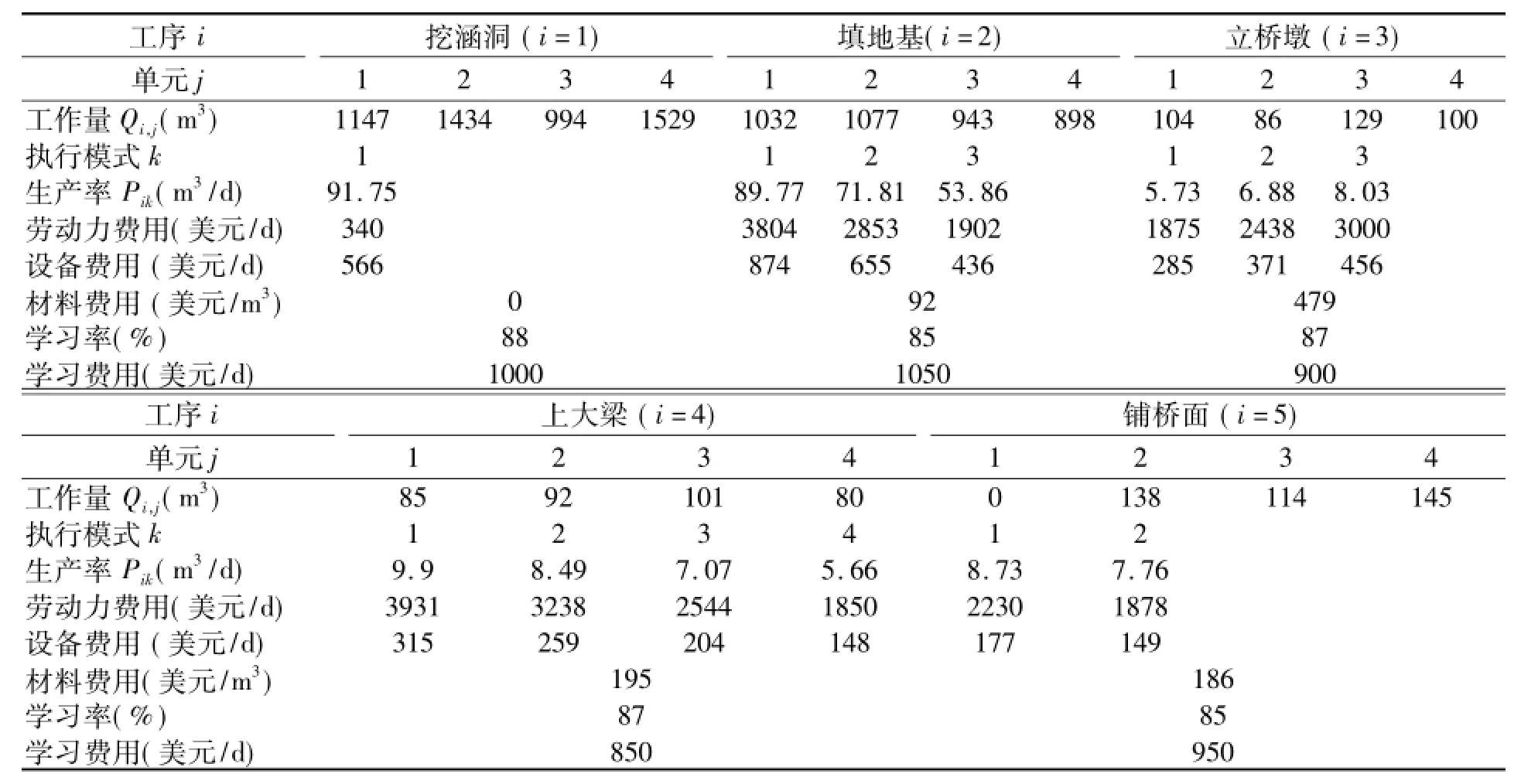
表1 项目数据
粒子群算法求解最小总成本如图2所示,项目总成本在图中的点A取得极小值,此时得到近似最优值1699242美元。粒子群算法的初始参数设置如下:迭代次数为100,种群规模为10,初始惯性权重最大值和最小值分别设置为wmax=0.9,wmin=0.4,学习因子c1=c2=1。

图2 粒子群算法求解最小总成本
表2列出了与不考虑学习效应方案对比下学习效应对项目费用的影响。为了维持一定的学习效应,额外增加了项目的管理费用(学习费用)。但是,由于学习效应使得项目总工期缩短了19天,由此造成项目的直接成本、间接成本、设备租赁费、延迟(提前)完工惩罚(奖励)费用等大幅降低,从而总成本也大幅降低。表3列出了是否考虑学习效应情况下的最低成本方案,从中可以看出,考虑学习效应后使得最优方案中部分工序执行模式的选择也发生了改变,例如,在不考虑学习效应情况下,工序(4)“上大梁”选择的执行模式3;而考虑学习效应后则选择执行模式2。总体看来,考虑学习效应对该项目调度方案优化效果非常明显。

表2 有无学习效应下的费用情况
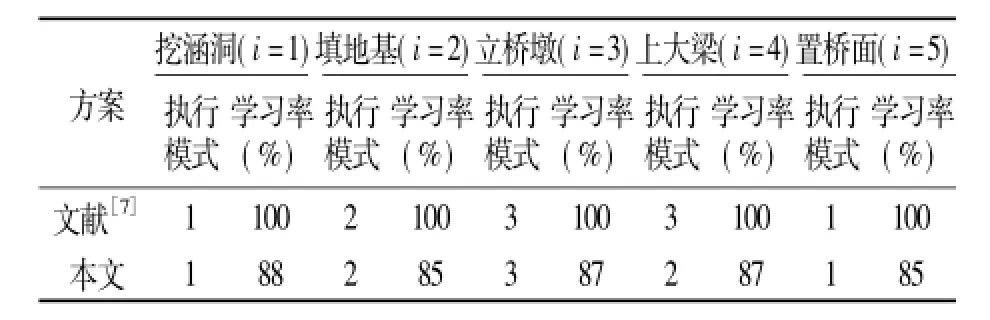
表3 在有无学习效应情况下最小成本方案选择
5 结语
本文探讨了学习效应对重复性项目成本的影响以及在重复性项目成本和工期决策优化中的应用。利用学习效应缩短项目工期、降低项目总成本的特点,本文建立了考虑学习效应情况下的最低成本方案决策模型,并设计了一种改进的粒子群算法求解。该算法同时还能满足重复性项目中各工序对工作连续性的要求。与事先不考虑学习效应的实施方案相比,考虑学习效应后项目计划者将把学习效应可能提高的生产率考虑到施工进度中,使得重复性项目的总工期缩短,工程计划将更加贴近工人的实际工作效率。项目计划人员可以充分利用学习效应获得更优的工程方案,对减小项目的总成本和制定科学的施工方案具有重要意义。
在项目施工过程中考虑学习效应的同时,由于施工中断等情况工人也可能会出现遗忘效应。所以,将学习效应和遗忘效应同时考虑到重复性项目优化问题将是本文后续的研究工作。
[1]Harris R B,Ioannou PG.Scheduling projectswith repeating activities[J].Journal of Construction Engineering and Management,1998,124(4):269-278.
[2]Lucko G.Productivity schedulingmethod:Linear schedule analysis with singularity functions[J].Journal of Construction Engineering and Management,2009,135 (4):246-253.
[3]张立辉,邹鑫,乞建勋.通过延迟阶跃函数求解重复性项目控制路线的方法研究[J].中国管理科学,2013,21(3):118-126.
[4]Kallantzis A,Soldatos J,Lambropoulos S.Linear versus network scheduling:a criticalpath comparison[J].Journal of construction engineering and management,2007,133(7):483-491.
[5]Zhang Lihui,Pan Chuyun,Zou Xin.Criticality comparison between the repetitive scheduling method and the network model[J].Journal of Construction Engineering and Mana-gement,2013,139(10):135-141.
[6]张立辉,邹鑫,乞建勋.考虑软逻辑的重复性项目离散时间费用权衡问题[J].系统工程学报,2013,28(4):554-561.
[7]Hyari K H,El-Rayes K,El-Mashaleh M.Automated trade-off between time and cost in planning repetitive construction projects[J].Construction Management and Economics,2009,27(8):749-761.
[8]Georgy M E.Evolutionary resource scheduler for linear projects[J].Automation in Construction,2008,17 (5):573-583.
[9]Tang Y,Liu R,Sun Q.Study and Application on China Railway Construction Project Scheduling Model Based on Resource Leveling[M].Berlin:Springer Berlin Heidelberg,2013.
[10]De P,James Dunne E,Ghosh JB,et al.The discrete time-cost tradeoff problem revisited[J].European Journal of Operational Research,1995,81(2):225-238.
[11]Hindelang T J,Muth JF.A dynamic programming algorithm for decision CPM networks[J].Operations Research,1979,27(2):225-241.
[13]Vanhoucke M,Debels D.The discrete time/cost tradeoff problem:extensions and heuristic procedures[J].Journal of Scheduling,2007,10(4-5):311-326.
[14]Zhang L,Zou X,Su Z.GA optimization model for time/cost trade-off problem in repetitive projects considering resource continuity[J].Applied Mathematics&Information Sciences,2013,7(2):611-617.
[15]Long L D,Ohsato A.A genetic algorithm-based method for scheduling repetitive construction projects[J].Automation in Construction,2009,18(4):499-511.
[16]Wright T P.Factors affecting the cost of airplanes[J].Journal of the Aeronautical Sciences,1936,3(4):122-8.
[17]Arditi D,Tokdemir O B,Suh K.Effect of learning on line-of-balance scheduling[J].International Journal of Project Management,2001,19(5):265-277.
[18]Couto JP,Teixeira JC.Using linearmodel for learning curve effect on highrise floor construction[J].Construction Management and Economics,2005,23 (4):355-364.
[19]Pellegrino R,Costantino N,Pietroforte R,etal.Construction of multi-storey concrete structures in Italy: patterns of productivity and learning curves[J].Construction Management and Economics,2012,30(2): 103-115.
[20]Blancett R S.Learning from productivity learning curves[J].Research-Technology Management,2002,45(3): 54-58.
[21]Stanford Research Institute.An improved rational and mathematical explanation of the progress curve in airframe production[R].Stanford:Stanford Research Institute,1949.
[22]Everett JG,Farghal S.Learning curve predictors for construction field operations[J].Journal of construction engineering and management,1994,120(3):603-616.
[23]Carr G W.Peacetime cost estimating requires new learning curves[J].Aviation,1946,45(4):220-228.
[24]Moselhi O,El-Rayes K.Scheduling of repetitive projectswith cost optimization[J].Journal of Construction Engineering and Management,1993,119(4):681-697.
[25]Eberhart R C,Shi Y.Particle Swarm Optim ization:Developments,Applications and Resources[C]//Evolutionary Computation.California:IEEE,2001,1:81-86.
The Cost Op tim ization Prob lem in Repetitive Construction Projects Considering Learning Effect
ZHANG LI-hui,XIONG Jun,DE Ge-ji-ri-fu
(School of Economic and Management,North China Electric Power University,Beijing 102206,China)
The phenomenon of the learning effect is very common in repetitive construction projects.However,it has not been considered in the time/cost trade-off analysis.In this paper,the cost optimization problem in repetitive construction projects with the learning effect was studied,while meeting a prescribed deadline.The influence of the learning effect on the total project cost was analyzed,and then the mathematical formulation of the current problem was proposed.In order to solve this problem,an improved PSO algorithm was designed.The effectiveness of the proposed algorithm was verified by an illustrative example and the result indicates that considering the learning effect in scheduling provides more potential to reduce project duration and cost.The research presented in this paper can help the planner to establish amore realistic and reasonable planning.
learning effect;repetitive construction projects;cost optimization problem
TB114.1
A
2095-0985(2015)02-0054-06
2014-11-03
2015-03-01
张立辉(1974-),男,湖南宁乡人,教授,博士,研究方向为工程管理(Email:ncepuxiongjun@126.com)
国家自然科学基金(71171079;71271081)
