棒束通道内两相流动摩擦阻力特性分析

田齐伟，阎昌琪，孙立成，闫超星

（哈尔滨工程大学 核安全与仿真技术国防重点学科实验室，黑龙江 哈尔滨 150001）

棒束通道内两相流动摩擦阻力特性分析

田齐伟，阎昌琪＊，孙立成，闫超星

（哈尔滨工程大学 核安全与仿真技术国防重点学科实验室，黑龙江 哈尔滨 150001）

常温常压下，对竖直3×3棒束通道内气液两相流动阻力特性进行了实验研究。利用所获得的实验数据，对8种典型的两相流动摩擦压降计算模型进行了评价。结果表明，均相模型在两相流速较高时精度较高，在两相流速较低时则偏差较大。分相模型中，Friedel模型和Lombodi-Pedrocchi模型不适用于本实验条件下棒束通道内气液两相流动摩擦压降的计算。Chisholm C模型、Zhang-Mishima模型、ChisholmB模型、Mishima-Hibiki模型及L.Sun模型的预测值与实验值的平均相对误差介于20%～30%之间。基于实验数据，通过修正ChisholmC模型的C系数，给出一个新的修正模型，其计算值与实验值符合良好。

棒束通道；两相流动；摩擦阻力；ChisholmC模型

棒束型燃料元件作为压水反应堆、沸水反应堆堆芯的主体结构，其内部的流动和换热特性对反应堆的设计和安全运行起着至关重要的作用。棒束通道由于其流道结构的复杂性，通道内的流动阻力特性与常规圆管有很大不同。准确计算棒束通道内的流动阻力特性，一方面可降低主泵功率的设计裕量，有效减少厂用电损失，另一方面，可更准确地计算堆内冷却剂的流量分配，提高反应堆的设计水平和安全性。

目前，棒束通道两相摩擦压降的计算大多采用基于圆管的计算方法，但由于棒束通道内流动的复杂性，其有效性还有待考证。因此，本文结合3×3棒束通道气液两相流动摩擦压降实验数据，对相应的计算方法在棒束通道内的适用性进行评价，并在此基础上提出相应的修正方法。

图1 实验系统流程图Fig.1 Schematic diagram of experimental apparatus

1 实验装置

实验系统（图1）由水循环回路、气回路、实验段和数据采集系统组成。实验以常温常压（20℃，0.1MPa）下的空气和水为工质，空气经压气机压缩，通过减压阀将流量计入口空气压力维持在0.3MPa。空气流过气体流量计后，进入混合腔，并与水进行混合，之后流入实验段。水循环驱动压头由多级离心泵提供，水依次流经流量调节阀、流量计、混合腔和实验段。在实验段出口，气液混合物依靠重力自然分离，空气排入大气，水则返回水箱。

棒束实验段截面如图2所示，外壳采用34mm×34mm的正方形有机玻璃通道，内部9根（3×3）有机玻璃棒呈正方形排列，棒径为8mm，棒中心距为11mm，外侧棒中心距外壳6mm。实验段总长2 000mm，有机玻璃棒通过3个定位格架进行固定。实验段通过法兰连接到实验回路上。

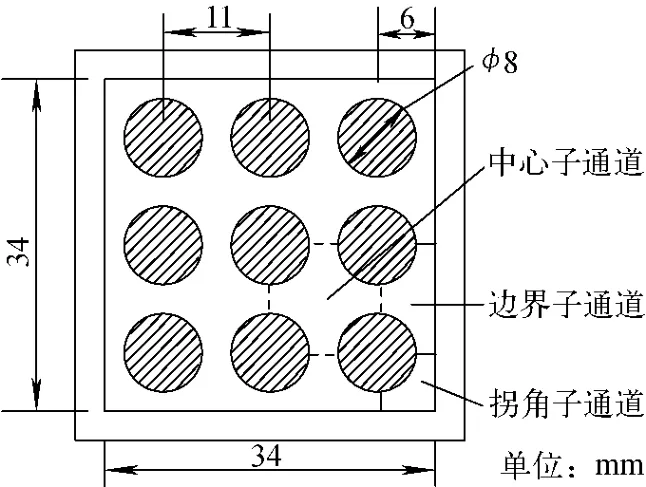
图2 棒束实验段结构Fig.2 Structure of rod bundle channel

实验中采集的数据主要包括气流量、水流量、温度及实验段内的压力等。气流量通过3个气体质量流量计测量，型号分别为GFM17、GFM37、GFM57，对应量程依次为0～10、0～50、0～200L／min，精度等级均为1级。水流量通过德国E＋H的PROMASS83质量流量计测量，量程为0～6 500kg／h，0.1级精度。水温在水箱回水口取样测量，气体温度以室温为准。沿程静压由GE公司的UNIK5000型压力传感器测量，精度等级为0.04。两个压力传感器的量程分别为0～100、0～200kPa，分别布置在距通道入口1 060mm和1 410mm处的两个定位格架之间。流量和对应压力信号通过NI数据采集系统传输给计算机，采样频率为256Hz。

实验在常压和室温下进行，气液两相表观速度分别为0.094～5.303m／s和0.196～1.793m／s。

2 实验数据处理与误差分析

竖直绝热条件下，棒束通道内两相流动总压降Δp由重位压降Δpgr和摩擦压降Δpf两部分组成。

重位压降Δpgr可按下式计算：

其中：α为截面含气率；g为重力加速度，m／s2；h为两测压点间的高度差，m；ρg、ρl分别为气液两相密度，kg／m3。

对于棒束通道内截面含气率的计算方法，Coddington等［1］依据大量实验数据进行了分析，发现Chexal-Lellouche［2］模型的效果较好，特别是在低压条件下。因此本文采用此模型计算通道内截面含气率，方法如下：

其中：jg、j分别为气相表观速度与气液混合物表观速度，m／s；C0为分布参数；≪vgj≫为漂移速度，m／s。C0由下式计算：

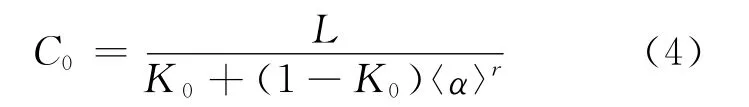
L为与压力和截面含气率有关的参数，按式（5）计算，参数C1与系统压力p及临界压力pcrit有关。〈α〉为截面含气率平均值，在此等于α。

K0为与两相相对密度及雷诺数有关的参数，计算方法见式（7）～（9），其中参数B1与雷诺数有关，Re为分相雷诺数中的最大值。

其中：Rel为分液相雷诺数；Reg为分气相雷诺数。

参数r与两相相对密度及雷诺数有关。

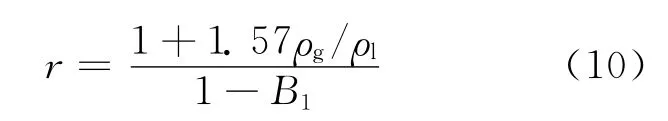
式（3）中的≪vgj≫按下式计算：

其中：σ为表面张力系数，N／m；Δρ为气液两相密度差，kg／m3；修正参数C2与两相密度有关。

截面含气率需迭代计算，迭代初值采用体积含气率β，直至迭代收敛。计算出截面含气率，便可从总压降中剥离出摩擦压降。

本文采用文献［3］中的不确定度计算方法分析测量参数的误差范围。各类不确定度分析结果列于表1。其中，A类不确定度ΔA指根据所测数据统计分析得出的不确定度；B类不确定度ΔB是指仪表及采集系统引入的系统误差；使用均方根合成法表示总不确定度Δ。

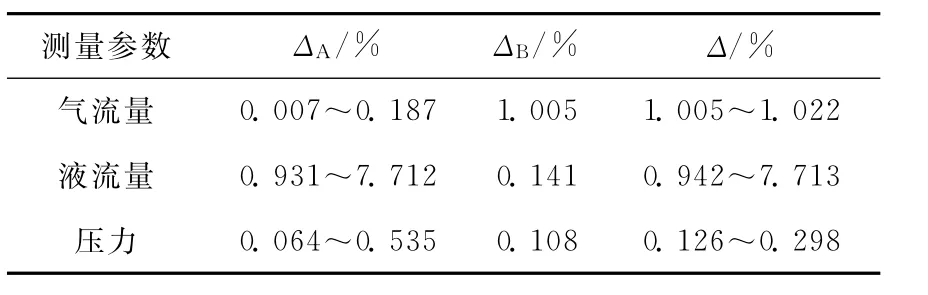
表1 测量参数的不确定度Table 1 Uncertainties of measured parameters

3 计算模型评价

基于棒束通道实验数据，本文对均相模型和分相模型中的Chisholm B／C模型［4］、Friedel模型［5］、Lombodi-Pedrocchi模型［6］、Zhang-Mishima模型［7］、Mishima-Hibiki模型［8］、L.Sun模型［9］等共8种两相摩擦压降计算方法的适用性进行了评价分析。

单相摩阻系数的计算，采用Cheng等［10］的棒束通道摩阻系数计算方法，将棒束通道划分为中心子通道、边界子通道和拐角子通道3种类型（图2）。棒束通道与其子通道的摩阻系数均按下式计算：

其中：λ为摩阻系数；K为摩阻系数几何因子；Re为雷诺数；角标i＝1、2、3、b分别对应中心子通道、边界子通道、拐角子通道及棒束整体；层流时m＝1，紊流时m＝0.18。

子通道摩阻系数几何因子Ki与棒束中心距P与棒径D的比值P／D有关，即：

其中，a、b1、b2取决于流动状态及P／D值。

棒束整体几何因子为：

其中：De为通道当量直径，m；Si＝NiAi／Ab，Ni为各类子通道数目，Ai为对应通道面积，m2。

图3为摩擦压降梯度各模型计算值与实验值的对比。相应的统计性分析结果列于表2。表中列出了各模型计算结果的平均相对误差以及相对误差在±30%、±50%以内数据点所占的比例。其中，平均相对误差（MRE）的计算方法为：

均相模型的MRE为24.64%，计算精度较高，但由图3可看出，其在摩擦压降相对较高时预测值很好，较低时偏差较大，说明均相模型不太适合于气液流速较低的工况。这可能是因为低流速下，气相由于浮力作用，相对速度快于液相，气液滑速比较大所致；高流速下气液搅混明显，两相运动过程更趋于均相流。

分相模型中Friedel和Lombodi-Pedrocchi模型的MRE分别为72.74%和95.72%，且相对误差在±30%、±50%以内的数据点所占比例很低，说明这两种模型并不适用于本实验条件下的棒束通道。L.Sun指出Friedel模型更适用于有机制冷剂的两相流动。而Lombodi-Pedrocchi模型适用于压力相对较高、气液密度差较小的两相流动工况。

图3 摩擦压降梯度各模型计算值与实验值比较Fig.3 Comparison between experimental data and calculated values of frictional pressure drop gradient by different models

此外，由表2可看出Zhang-Mishima模型、ChisholmC模型、L.Sun模型、Mishima-Hibiki模型、ChisholmB模型的MRE依次增大，但均介于20%～30%之间，预测精度相差不大。MRE相对较小的Zhang-Mishima模型和ChisholmC模型，在气液流速相对较低、摩擦压降相对较小的工况下，MRE的散度偏大，气液流速较高、摩擦压降较大时预测值偏低。ChisholmB模型和Mishima-Hibiki模型在摩擦压降相对较高时，预测效果较好，在摩擦压降较低时，预测值偏大。L.Sun模型在摩擦压降较小时，预测值偏高，而摩擦压降较大时，预测值偏低。

表2 不同模型误差的统计性分析Table 2 Statistical analysis of errors of different models

4 修正模型提出

ChisholmC模型中C系数的确定是以雷诺数等于2 000为界，划分为层流和紊流，进而给出C值。但在棒束通道内，针对层流和紊流的划分，不同学者的观点各异。Cheng等［10］认为棒束通道内层流和紊流的划分受P／D影响明显，且存在较大的过渡区。Rehme［11］认为棒束通道中不存在层流到紊流的突变，而存在一个摩阻系数指数值由－1到－0.2的渐变过程。当主流区达紊流时，两棒之间及棒与壁面之间的区域仍有可能处于层流状态。因此，以圆管临界雷诺数2 000为界划分流态进而确定C值的方法，并不适用于棒束通道，从而导致偏差较大。

基于上述原因，本文以ChisholmC模型为基础，通过对C系数进行修正，给出适合于棒束通道的摩擦压降计算方法。Chen等［12］认为ChisholmC模型的C系数与全液相雷诺数Relo及马蒂内利参数X有关。在此基础上，同时考虑Rel、Reg对C系数的影响，得出如下修正关系式：

摩擦压降梯度的修正关系式计算值与实验值的对比如图4所示。统计性分析表明，修正关系式计算值的平均相对误差为15.45%，相对误差在±30%及±50%范围内的数据点所占比例分别为88.81%和94.78%，总体效果好于其他模型，且提高了气液流速较低工况时的预测精度。

图4 摩擦压降梯度修正关系式计算值与实验值对比Fig.4 Comparison between predicted values by new correlation and experimental data of frictional pressure drop gradient

5 结论

以常温常压下的空气和水为工质，对竖直3×3棒束通道内的两相流动摩擦阻力特性进行了实验研究，并对8种两相摩擦压降计算方法的适用性进行了评价，得出的主要结论如下：

1）在两相流速较高时，气液两相搅浑明显，均相模型的预测精度较高，而两相流速较低时，由于浮力作用，滑速比偏大，均相模型预测偏差较大。

2）Friedel模型和Lombodi-Pedrocchi模型的预测结果偏差很大，不适用于计算常温常压下棒束通道内气液两相流动的摩擦压降。

3）Chisholm C模型、Zhang-Mishima模型、Chisholm B模型、Mishima-Hibiki模型及L.Sun模型的预测值与实验值的平均相对误差介于20%～30%之间，预测精度相差不大，但在一定参数范围内，偏差较大。

4）基于实验数据，以Chisholm C模型为基础，对C系数进行了修正，修正方法的计算值与实验值的平均相对误差为15.45%，对气液流速较低工况的预测效果较好。

本实验以空气和水为工质，对棒束通道内两相流动摩擦阻力特性进行了研究。相对于空气和水的两相流动，加热或冷凝实验中的气水两相流动由于相变而产生的传热和传质等过程，其流动特性更为复杂。对于加热及冷凝通道内的两相流动摩擦阻力特性的预测大多基于绝热通道阻力关系式，并考虑热平衡含气率等因素的影响。本实验研究可为加热或冷凝条件下的棒束通道内气水两相流动提供实验上的参考。

［1］ CODDINGTON P，MACIAN R.A study of the performance of void fraction correlations used in the context of drift-flux two-phase flow models［J］.Nuclear Engineering and Design，2002，215：199-216.

［2］ CHEXAL B，LELLOUCHE G，HOROWITZ J，et al.A void fraction correlation for generalized applications［J］.Progress in Nuclear Energy，1992，27（4）：255-295.

［3］ 陆廷济，忽的敬，陈铭南.物理实验教程［M］.上海：同济大学出版社，2000：14-15.

［4］ CHISHOLM D.Pressure gradients due to friction during the flow of evaporating two-phase mixtures in smooth tubes and channels［J］.Int J Heat Mass Transfer，1973，16（2）：347-358.

［5］ FRIEDEL L.Improved friction pressure drop correlations for horizontal and vertical two-phase pipe flow［C］∥European Two-Phase Flow Group Meeting，Paper E2.［S.l.］：［s.n.］，1979.

［6］ HETSRONI G.多相流动和传热手册［M］.鲁钟琪，等译.北京：机械工业出版社，1993.

［7］ ZHANG W.Study on constitutive equations for flow boiling in mini-channels［D］.Japan：Kyoto University，2006.

［8］ MISHIMA K，HIBIKI T.Some characteristics of air-water flow in small diameter vertical tubes［J］.Int J Multiphase Flow，1996，22：703-712.

［9］ SUN L C，MISHIMA K.Evaluation analysis of prediction methods for two phase flow pressure drop in mini-channels［J］.Int J Multiphase Flow，2009，35（1）：47-54.

［10］CHENG S K，TODREAS N E.Hydrodynamic models and correlations for bare and wirewrapped hexagonal rod bundles-bundle friction factors，subchannel fraction factors and mixing parameters［J］.Nuclear Engineering and Design，1986，92：227-251.

［11］REHME K.Pressure drop performance of rod bundles in hexagonal arrangements［J］.Int J Heat Mass Transfer，1972，15：2 499-2 517.

［12］CHEN I Y，CHEN Y M.Two-phase flow pattern and frictional performance across small rectangular channels［J］.Applied Thermal and Fluid Science，2002，26（2）：389-407.

Analysis of Frictional Resistance of Two-phase Flow in Rod Bundle Channel

TIAN Qi-wei，YAN Chang－qi＊，SUN Li-cheng，YAN Chao-xing
（Fundamental Science on Nuclear Safety and Simulation Technology Laboratory，Harbin Engineering University，Harbin150001，China）

The experimental investigation of air-water two-phase flow resistance characteristics in a vertical channel with a 3×3rod bundle was carried out under atmospheric and room temperature conditions.Eight classical correlations for predicting frictional pressure drop of two-phase flow were evaluated against the experimental data.The experimental results show that the homogeneous model can predict the experimental data well at high flow rates，but with relatively large deviations at low flow rates.Both the Friedel model and the Lombodi-Pedrocchi model are not suitable any longer for the present case.The Chisholm C model，the Zhang-Mishima model，the Chisholm B model，the Mishima-Hibiki model and the L.Sun model can well predict the experimental data with mean relative errors in the range of 20%-30%.The Cfactor in the ChisholmC model was modified for giving a new correlation to predict the frictionalpressure drop of two-phase flow through rod bundles，showing agood agreement with the experimental data.

rod bundle channel；two-phase flow；frictional resistance；ChisholmCmodel

TL334

：A

：1000-6931（2015）05-0819-06

10.7538／yzk.2015.49.05.0819

2014-01-16；

2014-03-28

国家自然科学基金资助项目（11175050，51376052）

田齐伟（1988—），男，河北沧州人，硕士研究生，从事反应堆热工水力及气液两相流研究

＊通信作者：阎昌琪，E-mail：Changqi＿yan＠163.com