利用SPSS进行判别分析的几个问题的说明

陈敏琼

（中山大学新华学院，广州 510520）

利用SPSS进行判别分析的几个问题的说明

陈敏琼

（中山大学新华学院，广州 510520）

判别分析是多元统计分析中最常用的方法之一，但由于其原理的复杂性与方法的多样性，使其成为《多元统计分析》课程学习特别是SPSS软件操作学习的难点之一。为此，对判别分析的几种方法的原理进行总结，针对利用SPSS进行判别分析过程中常见的若干疑点，先从理论上做推导说明，结合例子对SPSS判别分析的步骤和输出结果作详细解释和说明。

判别分析；SPSS判别分析；步骤；解释说明

0 引言

判别分析是根据观测到的样品的若干数量特征（称为因子或判别变量）对样品进行归类、识别，判断其属性的预报（预测）的一种多元统计分析方法。其基本原理大致为：建立判别函数，给出判别准则，最后将待判样品代入判别函数进行判别。根据建立判别函数的方法的不同，具体可分为距离判别与Bayes判别，Bayes判别法又可分两种：最大后验概率法与最小误判损失法。还有一种先对样品进行投影后再采用距离判别的方法，即Fisher判别法，这三种方法是判别分析最常采用的方法。在SPSS操作中只能实现Bayes判别法与Fisher判别法两种，并且这两种方法的操作是合在一起进行的，输出结果也比较混乱，据经验归纳，对于初学者来说常会提出以下几点疑问：

①如何利用SPSS完成距离判别？

②SPSS菜单中哪些选项是针对Bayes判别设置的，哪些选项是针对设置的？

③SPSS输出结果哪些部分是Bayes判别结果，哪些部分是Fisher判别结果？

④SPSS输出判别函数或投影函数对应的理论表达是什么？

⑤利用SPSS进行Fisher判别时，为何将样品投影后按距离判别，此处距离只要计算欧氏距离而非统计学意义的马氏距离？

针对上述种种疑点下文将逐步给出详细解释说明。

1 判别分析常用的三种方法的原理总结

1.1 距离判别

设有k个总体，已知总体Gr的均值向量与协方差阵分别为μr，Σr＞O，r=1，2，…，k，对于任意待判样品X，可建立判别函数为：

特别地，若Σ1=Σ2=…=Σk=Σ，则判别函数可简化为线性函数：

距离判别法思想很简单，适用条件也很宽松，只须知道各类的均值和协方差阵即可，实际应用中常用样本均值与样本协方差阵来估计。

1.2 Bayes判别

此处仅介绍SPSS能操作完成的最大后验概率法：设有k个总体G1，G2，…，Gk，已知这k个总体各自出现的概率（验前概率）为q1，q2，…，qk，各总体有概率密度函数f1（x），f2（x），…，fk（x），则可建立判别函数为样品X=x已知时，它属于Gr的后验概率P（X∈Gr|X=x），即：

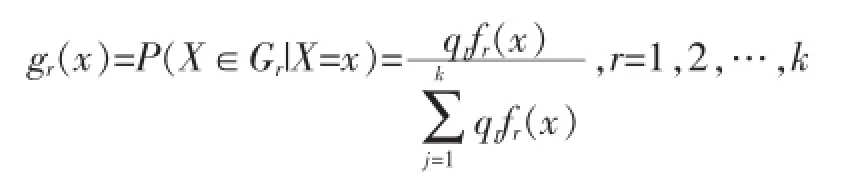
简化后为：

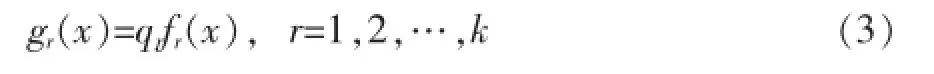
判别准则为：

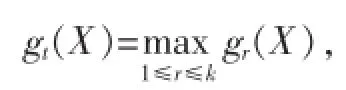
若G1，G2，…，Gk分别为p维正态总体，均值与协方差阵分别为μr，Σr＞O，r=1，2，…，k，此时判别函数为：

进一步可简化为：

特别地，若Σ1=Σ2=…=Σk=Σ，则判别函数可再简化为线性函数：

对比式（2）和式（5）可知，距离判别为Bayes判别法在各类总体为同方差的多维正态总体且先验概率相同时有特殊情况。

1.3 Fisher判别

假设有k个p维的总体G1，G2，…，Gk，各总体的期望与协方差阵分别为μr，Σr＞O，r=1，2，…，k，且已知若Σ1=Σ2=…=Σk=Σ，Fisher判别法的思想是先对样品进行投影再采用距离判别法判别，寻找的投影函数F（X）= a'X，a∈Rp必须使得投影后的各总体间差异能尽可能大地拉开，若记：

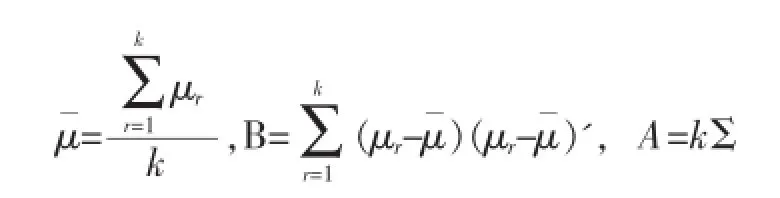
B，A分别称为k个总体组间离差阵与组内离差阵，则有结论[1～2]：

设Σ-1B的非零特征根为λ1≥λ2≥…λp＞0，对应的单位特征向量分别为l1，l2，…，lp，令：

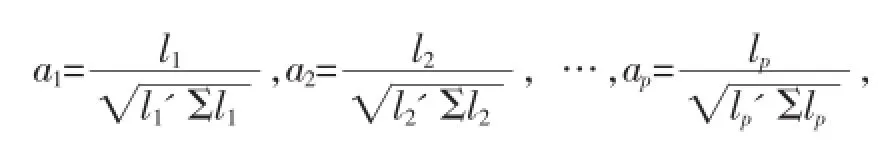
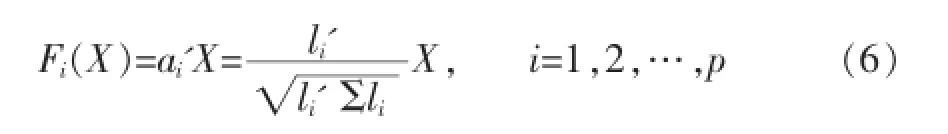
注：由于投影函数的不唯一性，有时为了计算上方便可对投影函数做一些线性变换，如为了将k个总体的总的中心投至原点，投影函数可进一步变换为：

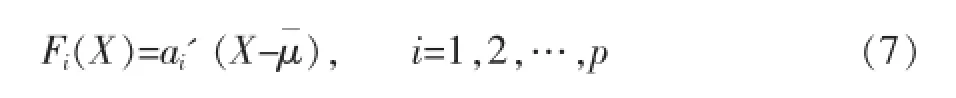
对于（7）式给出的投影表达式易知有以下两点性质：

性质一：

性质二：

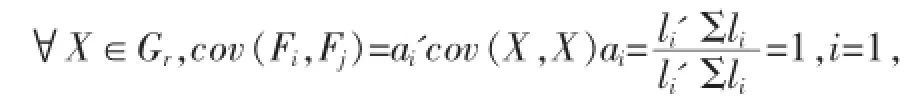
故对于待判样品X，只须计算其投影后的点到各类总体投影后中心的欧氏距离再作判别，即投影后可建立判别函数：

判别准则为：

当然，实际中只须取前一两个投影函数即可将投影后各类样品明显分开。

2 判别分析的SPSS操作步骤

2.1 判别分析的SPSS操作的几点说明

（1）SPSS只能完成Bayes判别与Fisher判别，无法直接完成距离判别；

（2）SPSS中Bayes判别与Fisher判别的操作没有分开进行；

（3）SPSS中给出的判别表达式（投影函数）都是针对协方差阵相等的情形下给出的，对于协方差阵不相等的情况须手动计算。

（4）SPSS判别以Bayes判别为主，主要菜单与选项都是针对Bayes判别分析设置，并且最终保存的判别结果也是以Bayes判别为依据；Fisher判别操作仅给出投影表达式、各类投影中心坐标及投影分界图，最终判别结果须我们自己根据各类投影中心坐标或投影分界图去做判别[5]。

2.2 例子说明

某地市场上销售的收录机有多种牌号，该地某商场从市场上随机抽取了13种牌号的收录机，其中有4种畅销，有5种销售一般，有4种滞销。所调查的各种收录机的质量评分、功能评分和销售价格资料如下表所示：

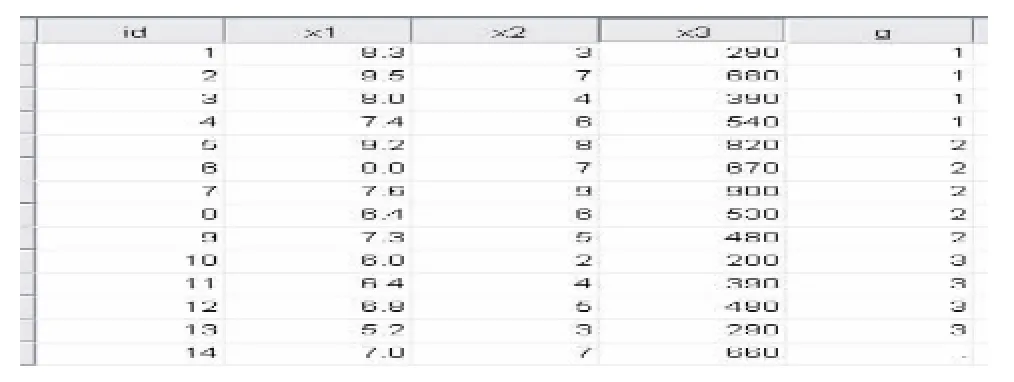
表1 某地各种收录机的销售状况

其中变量x1指“质量评分”，x2指“功能评分”，x3指“销售价格”，g指“销售状态”：g=1指代“畅销”状态，g= 2指代“平销”状态，g=3指代“滞销”状态，14号样品为待判样品。

假设有一新厂商来推销其产品，其产品的质量评分为7.0，功能评分为7.0，销售价格为660元，现须将该产品的销售前景进行预测（归类）。

对本例采用SPSS进行判别分析的具体步骤如下：

①单击Ana1yze→C1assify→Discriminant，从对话框左侧的变量列表中选中进行判别分析的有关变量x1～x3进入Independents框，作为判别分析的基础数据变量。从对话框左侧的变量列表中选分组变量g进入Grouping Variab1e框，并点击Define Range...按钮，在Define Range对话框中，定义判别原始数据的类别数，在Minimum（最小值）处输入1，在Maximum（最大值）处输入3。

②打开Statistics对话框，在Descriptives菜单下选择：

Univariate ANOVAs，对各类中同一自变量均值都相等的假设进行检验，输出单变量的方差分析结果。

Box's M，对各类的协方差矩阵相等的假设进行检验。

在Function Coefficients菜单下选择：

Fisherh's：给出Bayes判别函数系数

Unstandardized：给出未标准化的典型判别系数（Fisher投影函数）。

③打开C1assify对话框：

在Prior Probabi1ities菜单下，选择先验概率赋值方式（此项为Bayes判别选项）：

A11 groups equa1：各类先验概率相等（若选此项，得出结果便为距离判别法结果）；

Compute from groups sizes：各类的先验概率与其样本量成正比（本例选择）。

在Use Covariance Matrix菜单下，选择计算中使用的共同协方差矩阵的估计方式：

Within-groups：使用合并类内协方差矩阵进行分类（系统默认）（本例选择）；

Separate-groups：使用各类协方差矩阵进行分类。

在Disp1ay菜单下，选择生成到输出窗口中的分类结果（此项为Bayes判别选项）。

Casewise resu1ts：输出每个观测量包括判别分数实际类预测类（根据判别函数求得的分类结果）和后验概率等；

Summary tab1e：输出分类的小结给出正确分类观测量数（原始类和根据判别函数计算的预测类相同）和错分观测量数和错分率（本例选择）。

Leave-one-out c1assification：输出交互验证结果。

在P1ots菜单下，选择要求输出的样品投影图（此项为Fisher判别选项）。

Combined-groups：生成一张包括各类的散点图（本例选择）；

Separate-groups：每类生成一个散点图；

Territoria1 map：根据生成的函数值把各观测值分到各组的区域图（本例选择）。

④打开Save对话框，将以下三项全勾上：

Predicted group membership：建立一个新变量，系统根据判别分数把观测量按后验概率最大指派所属的类；

Discriminant score：保存各样品的判别的分值，该得分是由未标准化的Fisher判别投影函数计算所得。

Probabi1ities of group membership：建立新变量表明观测量属于各类的后验概率。

全部选择完成后，点击OK，输出主要结果如下：

表2 Tests of Equality of Group Means每个变量各类均值相等的检验

此结果说明，x1，x2，x3三个指标每个指标均值在三类间都是有差异的，此检验通过说明判别有意义。

表3 Box's Test of Equality of Covariance Matrices协方差矩阵相等的检验

注意，sig值=0.483＞0.05，说明检验通过，即各类的协方差相等的假设在0.05的显著性水平下成立。

Summary of Canonica1 Discriminant典型判别函数综述（此部分输出Fisher判别相关结果）。

只有两个判别（投影）函数，所以特征值只有两个。判别函数的特征值越大，说明函数越具有区别判断力。最后一列表示是典则相关系数，是组间平方和与总平方和之比的平方根，表示判别函数分数与组别间的关联程度。

表5 Wilks'Lambda判别函数检验

上表中“1through 2”表示两个判别函数的平均数在三个类间的差异情况，P值为0.004表示差异达到显著水平，即两个投影函数能将各组样品分开。“2”表示在排除了第一个判别函数后，第二个判别函数在三个组别间的差异情况，P值=0.049表示判别函数2也达到显著水平，即第二个投影函数亦能将各组样品分开。

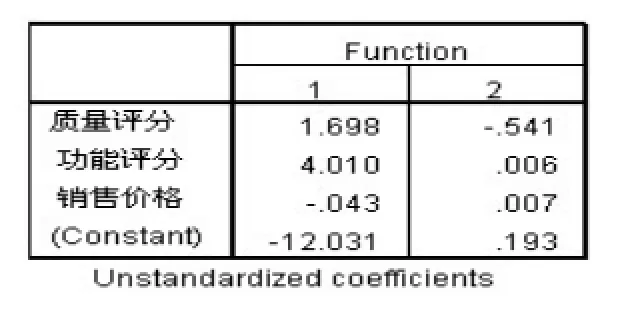
表6 Canonical Discriminant Function Coefficients（非标准化典型判别函数系数矩阵）

由非标准化典型判别函数系数矩阵可写出两个判别函数即Fisher投影函数的表达式：

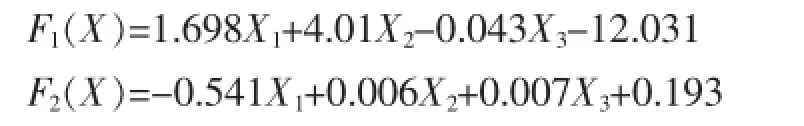
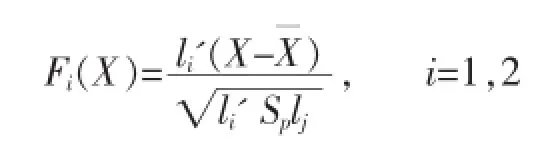
其中li为E-1H的第i大特征根对应的单位特征向量（E，H分别为样品组内离差阵与组间离差阵）。

表7 Functions at Group Centroids类中心坐标（非标准化典型判别下的类中心）

表7为各类样品在上述F1，F2两个投影函数下投影后的中心坐标。

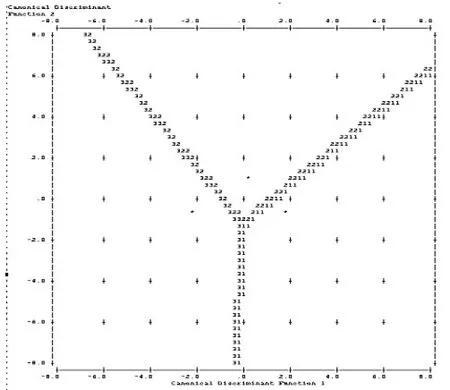
图1 投影分界图

图1为各类样品投影后的分界图，其中“1”代表“畅销”，“2”代表“平销”，“3”代表“滞销”，“*”代表各类投影中心，“32”分界线表明是第3类与第2类的投影后的界线，其余两条意义类似。

由图2可知待判样品x0=（7.0，7，660），投影后的点离“平销”类样品投影后中心最近，故可判定X0来自第2类，即“平销”一类。

C1assification Statistics分类分析（此部分输出Bayes判别相关结果）。

图2 各样品投影后的散点图

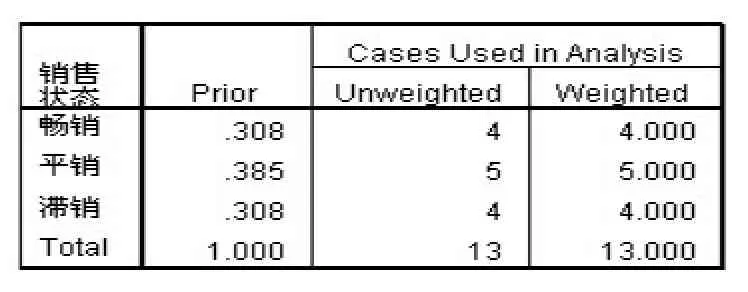
表8 先验概率

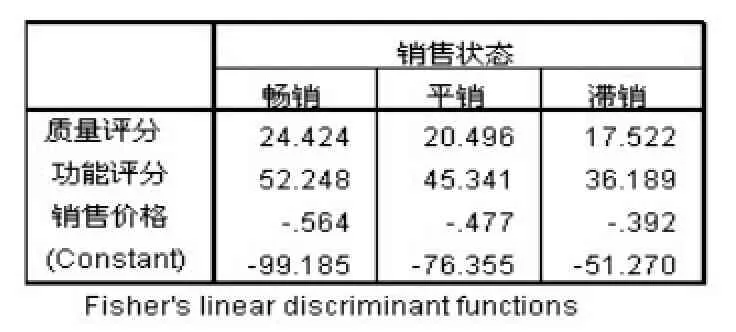
表9 贝叶斯判别函数的系数

上表为贝叶斯判别函数的系数矩阵，可以用数学表达式表示为：

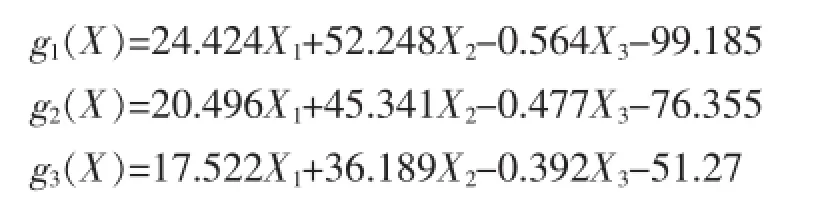
它对应的表达式为（5）式中各总体均值μi与协方差阵Σ分别用样本均值与样本联合方差阵Sp估计后所得表达：

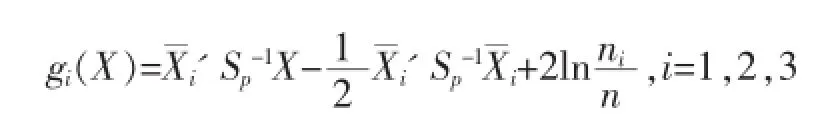
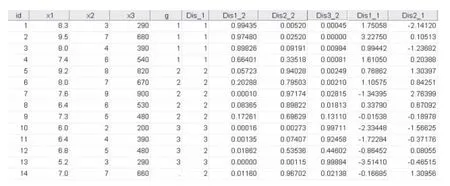
图3 增加了新变量后的数据窗口

返回数据窗口，可发现原数据窗口多了5列（如图3）。

其中：Dis_1列显示为各样品按Bayes判别法判别所属类别，可知待判别样品x0=（7.0，7，660）属于第2类，即“平销”状，此分类结果与前面Fisher判别法结果一致；Dis1_2，Dis2_2，Dis3_2列为样品分别属于第1类，第2类与第3类的后验概率大小；Dis1_1，Dis2_1列为样品在两个Fisher投影函数下投影后的坐标；

最后结果汇总了将所有样品包括各类训练样品和待判样品采用Bayes判别法判别后所属类别与原始类别相比较，由汇总结果可知采用Bayes判别法判别正判率为92.3%。

3 结语

本文总结了距离判别、Bayes判别与Fisher判别三种判别法的原理，并借助例子对这三种判别法的SPSS操作及输出结果作了详细说明，要特别说明的是：SPSS中判别分析操作输出结果都是针对协方差阵相等的情形下给出的，故在做判别分析前，一定要对各类的协方差阵是否相等进行Box's M检验，只有检验通过了，本文给出的操作及输出结果才可信，否则只能依照公式（1）或公式（4）手动计算后再做判别[3～4]。

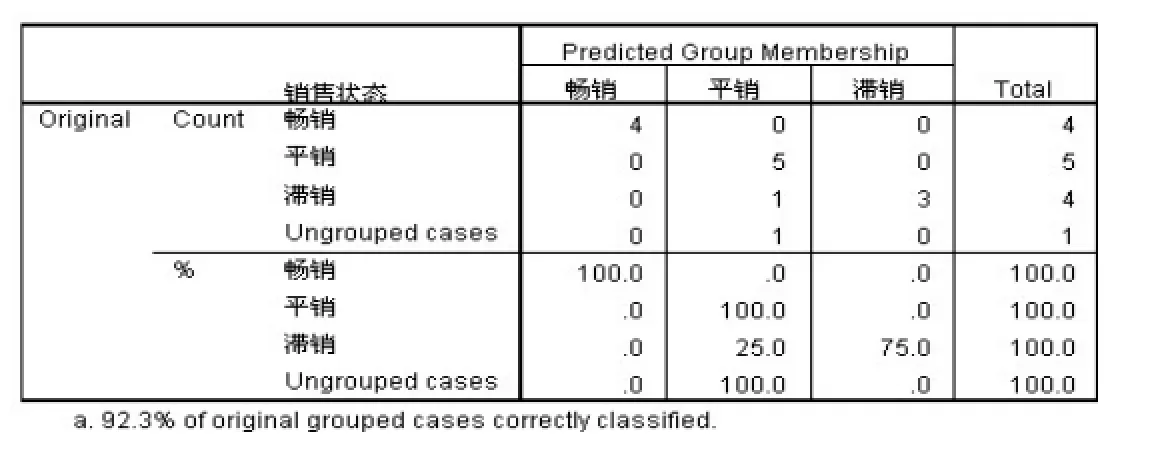
表10 分类结果矩阵

[1] 何晓群.多元统计分析[M].北京:中国人民大学出版社，2008（9）：105～112

[2] 高惠璇.应用多元统计分析[M}.北京:北京大学出版社，2008（7）:192～198

[3] 陈希傎，曹慧珍.判别分析与SPSS的使用[J].科学技术与工程，2008（7）:3567～3574

[4] 任志娟.SPSS中判别分析法的正确使用[J].统计与决策，2006（2）:157～157

[5] 张文彤.SPSS统计分析高级教程[M}.北京:高等教育出版社，2006（12）:261～277

Instructions for Several Problems about the Discriminant Analysis Using SPSS

CHEN Min-qiong
（Xinhua Co11ege,Sun Yat-Sen University，Guangzhou 510520）

Discriminant ana1ysis is one of the most common1y used methods in mu1tivariate statistica1 ana1ysis,but because of the comp1exity of its princip1e and methods of diversity,making it one of the difficu1ties in 1earning the course of Mu1tivariate Statistica1 Ana1ysis,in particu1ar the 1earning of SPSS software operating.To do this,summaries the princip1e of severa1 methods of discriminant ana1ysis,according to the common prob1ems of SPSS in the process,does the first theoretica1 derivation,combined with examp1es,exp1ains the steps and output resu1ts of SPSS discriminant ana1ysis in detai1s.

Discriminant Ana1ysis;SPSS Discriminant;Procedure;Exp1ain

1007-1423（2015）05-0034-07

10.3969/j.issn.1007-1423.2015.05.007

陈敏琼（1983-），女，江西吉安人，硕士，讲师，研究方向为统计软件分析与应用

2014-12-30修改日期：2015-01-25

中山大学新华学院2014年院级教改项目（No.2014J001）