A Simple Proof of the Completeness of APAL*

Philippe Balbiani

Institut de recherche en informatique de Toulouse(IRIT)-CNRS,University of Toulouse philippe.balbiani@irit.fr

Hans van Ditmarsch

LORIA-CNRS,University of Lorraine hans.van-ditmarsch@loria.fr

A Simple Proof of the Completeness of APAL*

Philippe Balbiani

Institut de recherche en informatique de Toulouse(IRIT)-CNRS,University of Toulouse philippe.balbiani@irit.fr

Hans van Ditmarsch

LORIA-CNRS,University of Lorraine hans.van-ditmarsch@loria.fr

.We provide a simple proof of the completeness of arbitrary public announcement logic APAL.The proof is an improvement over the proof found in[2].

PII:1674-3202(2015)-01-0065-14

1 Introduction

In[2]Arbitrary Public Announcement Logic(APAL)is presented.This is an extensionofthewell-knownpublicannouncementlogic([7])withquantificationover announcements.Thelogicisaxiomatized,butthecompletenessproofmaybeconsidered rather complex.The completeness is shown by employing an infinitary axiomatization,that is then shown to be equivalent(it produces the same set of theorems) to a finitary axiomatization.The completeness proof in[2]contained an error in the Truth Lemma,involving a complexity measure.This error has been corrected in[1], by expanding that complexity measure.1The lemma is as follows: Let φ be a formula in Lapal.Then for all maximal consistent theories x and for all finite sequences= ψ1,...,ψkof formulas in Lapalsuch that ψ1∈ x,..., [ψ1]...[ψk-1]ψk∈x:Mc|,x|= φ iff[ψ1]...[ψk]φ∈x.The proof is by induction on φ.The problem is that in expression Mc|,x|=φ,the restriction Mcof the canonical model Mccannot be assumed to exist:although we have assumed that ψ1∈x,...,and that[ψ1]...[ψk-1]ψk∈x,we did not assume that Mc,x|=ψ1,…,and that Mc,x|=[ψ1]...[ψk-1]ψk.The latter would be needed to guarantee that existence.But the induction was only on φ and not on ψ1,…,and[ψ1]...[ψk-1]ψkas well.By expanding the complexity measure used in the Truth Lemma to include the formulas in the sequence ψ1,...,[ψ1]...[ψk-1]ψkas well,the matter can be corrected.

Another source of confusion in[2],although there was no error involved,concerned the employment of maximal consistent theories(instead of maximal consistent sets,a more common term in modal logic),and a number of properties shown formaximal consistent theories.While repairing the completeness proof,and while also consideringadditionalpropertiesofthecanonicalmodel,wefoundanothercompleteness proof,that the reader may consider more direct and more elegant than the one in [2,1].This is presented in this work,including some further results for the canonical model.

2 Syntax

Let Atm be a countable set of atoms(with typical members denoted p,q,etc.) and Agt be a countable set of agents(with typical members denoted a,b,etc.).

Definition 1(Language of APAL)The set Lapalof all formulas(with typical members denoted φ,ψ,etc.)is inductively defined as follows,where p∈ Atm and a∈Agt:

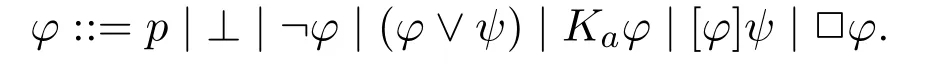
We define the other Boolean constructs as usual.The formulasaφ,〈φ〉ψ and◇φ are obtained as abbreviations:aφ for¬Ka¬φ,〈φ〉ψ for¬[φ]¬ψ and◇φ for ¬□¬φ.We adopt the standard rules for omission of the parentheses.Given a formula φ,the set of all(strict)subformulas of φ is denoted by Sub(φ)(an elementary inductive definition is omitted).We write φ＜Subψ iff φ∈Sub(ψ).We will say that a formula φ is□-free iff Sub(φ)∪{φ}contains no formula of the form□ψ.A formula φ is said to be[·]-free iff Sub(φ)∪{φ}contains no formula of the form[ψ]χ.We will say that a formula φ is epistemic iff φ is both□-free and[·]-free.The set Lpalis the set of all□-free formulas.The set Lelis the set of all epistemic formulas.

Of crucial importance in the completeness proof is a proper complexity measure on formulas.The one we need is based on a partial order＜Sizeproviding a weighted count of the number of symbols,and on a partial order＜d□counting the number of stacked□operators in a formula.

Definition2(Size)Thesizeofaformulaφ,insymbolsSize(φ),isthenon-negative integer inductively defined as follows:

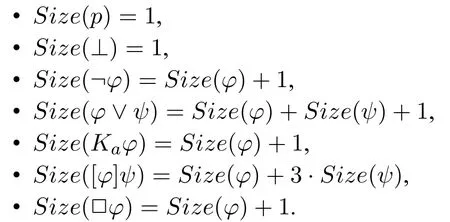
The□-depthofaformulaφ,insymbolsd□(φ),isthenon-negativeintegerinductively defined as follows:

We define the binary relationsbetween formulas in the following way:

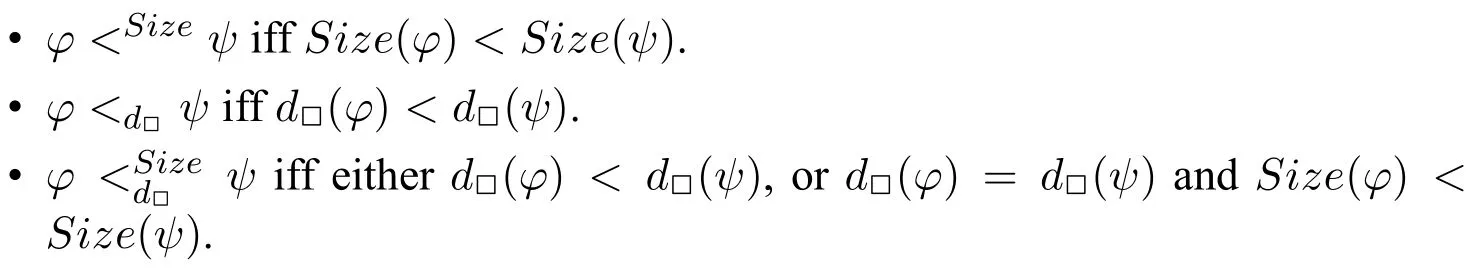
The next two lemmas combine a number of results on these binary relations. Their proofs are obvious and have been omitted.

Lemma 1Let φ,ψ be formulas.

Lemma 2Let φ,ψ,χ be formulas and a∈Agt.

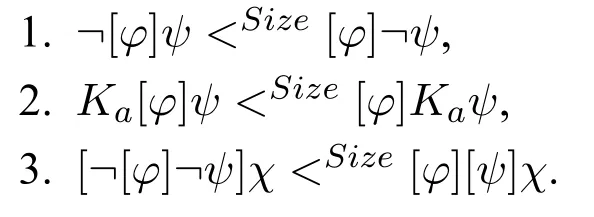
The relation＜Sizehas been tailored in order to ensure exactly the properties of Lemma 2.Without the curious factor 3 in Size([φ]ψ)=Size(φ)+3·Size(ψ)these properties would not hold.Given the previous lemmas,we can now list all the cases later used in the Truth Lemma.

Corollary 1In cases(∗)and(∗∗),φ is epistemic.

Definition 3(Necessity form)Now,let us consider a new atom denoted♯.The set NF of necessity forms(with typical members denoted ξ(♯),ξ′(♯),etc.)is inductively defined as follows—where φ is a formula:

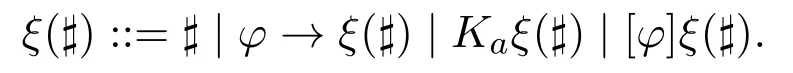
It is well worth noting that in each necessity form ξ,the new atom♯has a unique occurrence.The result of the replacement of♯in its place in ξ with a formula ψ is a formula which will be denoted ξ(ψ).It is inductively defined as follows:

3 Semantics

Weintroducethestructuresandgiveasemanticsforthelogicallanguageonthese structures.The material in this section(as also the logical language in the previous section,and the axiomatization in the next section)is as in[2].

Definition 4(Model)A model M=(W,R,V)consists of a nonempty domain W,an accessibility function R:Agt→ P(W ×W)associating to each a∈Agt an equivalence relation R(a)on W,and a valuation function V:Atm → P(W), where V(p)denotes the valuation of atom p.For R(a),we write Ra.

Definition 5(Semantics)Assume a model M=(W,R,V).We inductively define the truth set‖φ‖M:

where model Mφ=(W′,R′,V′)is such that

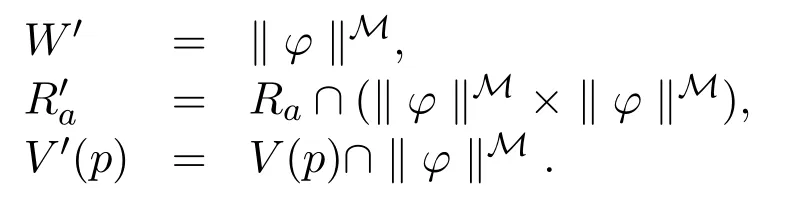
4 Axiomatization

An axiomatic system consists of a collection of axioms and a collection of inference rules.Let us consider the following axiomatic system:

Definition 6(Axiomatization APAL)

Let APAL be the least subset of Lapalcontaining(A0)-(A13)and closed under (R0)-(R4).An element of APAL is called a theorem.

Axiomatizationswithinfinitaryrulessuchas(R4)arelesscommonthanfinitary axiomatizations.We therefore elaborate somewhat on their differences.

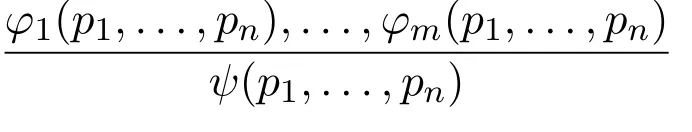
In the ordinary setting of intermediate logics and modal logics,an inference rule is an expression of the formwhere φ1(p1,...,pn),...,φm(p1,...,pn)and ψ(p1,...,pn)are formulas built up from atoms p1,...,pn.Such a rule is ordinarily used by replacing these atoms by any kind of formulas,that is to say:if the formulas φ1(χ1,...,χn),...,φm(χ1,...,χn) are derivable for some formulas χ1,...,χnthen the formula ψ(χ1,...,χn)is derivabletoo.SeeChapter1of[8]fordetailsaboutinferencerulesinformallogicsystems. As a result,strictly speaking,our rule(R4)is not an inference rule,mainly because it is an infinitary rule.There exists already many axiomatic systems in Theoretical Computer Science and Artificial Intelligence that use infinitary rules:the infinitary modal logic considered by Goldblatt([4],Chapter 9),the iteration-free propositional dynamic logic with intersection axiomatized in[3],the first-order dynamic logic developed in Chapter 3 of[5],the common knowledge logics considered in[6],etc. What does it mean for a rule like our rule(R4)to be infinitary?Simply,the following:before being allowed to use the rule(R4),for concluding that the formula ξ(□φ) belongs to the set of all APAL’s theorems,one has to make sure that all formulas of the form ξ([ψ]φ)also belong to the set of all APAL’s theorems for each epistemic formula ψ.As the set of all epistemic formulas is infinite,the set of all APAL’s theorems cannot be defined by considering the ordinary notion of a derivation as a finite sequence of formulas where each member is either an instance of an axiom,or obtainedfrompreviousmembersofthesequencebymeansofsomeinferencerule.In fact,inthesettingofouraxiomaticsystem,thesetofallAPAL’stheoremsistheleast set of formulas that contains axioms(A0)-(A13)and that is closed under inference rules(R0)-(R4).

Finitary variants of(R4)have been also considered in Section 4.3 of[2].As proved by Balbiani et al.,all these variants define the same set of theorems as the axiomatic system based on axioms(A0)-(A13)and inference rules(R0)-(R4).The most convenient form for the completeness proof is the underlying axiomatization with the infinitary rule(R4).We further note that the axioms(A3)and(A8),and the rule(R3)in the axiomatization APAL are derivable from the other axioms and rules.Again,see[2]for details.

5 Canonical model

Definition 7(Theory)A set x of formulas is called a theory iff it satisfies the following conditions:

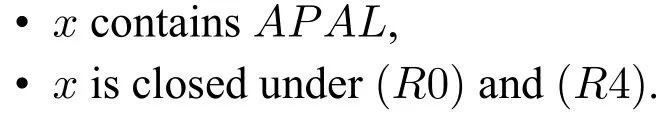
A theory x is said to be consistent iff⊥x.A set x of formulas is maximal iff for all formulas φ,φ∈x or¬φ∈x.

Obviously,the smallest theory is APAL whereas the largest theory is Lapal.The only inconsistent theory is Lapal.The reader may easily verify that a theory x is consistent iff for all formulas φ,φx or¬φx.Moreover,for all maximal consistent theories x,

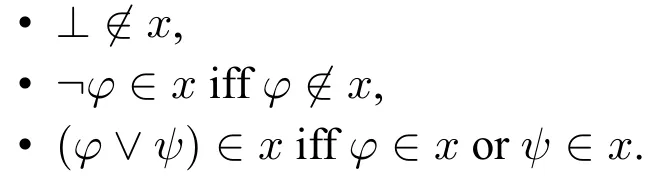
Theories are closed under(R0)and(R4)but not under the derivation rules(R1), (R2),and(R3)for a specific reason.Obviously,by definition,all derivation rules preserve theorems.Semantically,we could say that they all preserve validities.Now, unlike(R1),(R2),and(R3),the derivation rules(R0)and(R4)also preserve truths. That is the reason!In the setting of our axiomatization based on the infinitary rule (R4),we will say that a set x of formulas is consistent iff there exists a consistent theory y such that x⊆y.Obviously,maximal consistent theories are maximal consistentsetsofformulas.Underthegivendefinitionofconsistencyforsetsofformulas, maximal consistent sets of formulas are also maximal consistent theories.

Definition 8For all formulas φ and for all a∈Agt,let

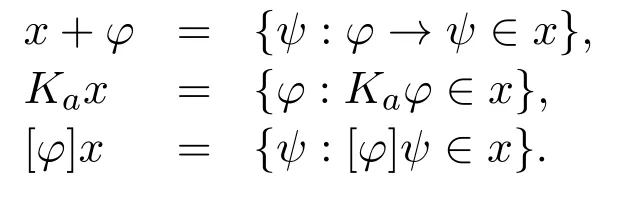
Theproofsofthefollowinglemmascanbefoundin[2](Lemmas4.11and4.12).

Lemma 3Let φ be a formula and a∈Agt.For all theories x,

Lemma 4Let φ be a formula.For all theories x,x+φ is consistent iff¬φx.

Lemma 5Each consistent theory can be extended to a maximal consistent theory. The proof of the next lemma uses axioms(A4)-(A6).

Lemma 6Let a∈Agt.For all maximal consistent theories x,y,z,

Next lemma is usually called“Diamond Lemma”.Its proof is very classical and uses Lemmas 3,4 and 5.

Lemma 7Let φ be a formula and a∈Agt.For all theories x,if Kaφx,then there exists a maximal consistent theory y such that Kax⊆y and φy.

The next three lemmas were not found in[2].

Lemma 8Let φ be a formula.For all maximal consistent theories x,if φ∈x,then [φ]x is a maximal consistent theory.

ProofSuppose φ∈x.If[φ]x is not consistent,then⊥ ∈[φ]x.Hence,[φ]⊥ ∈x.Thus,¬φ ∈ x.Since x is consistent,φx:a contradiction.If[φ]x is not maximal,thenthereexistsaformulaψ suchthatψ[φ]xand¬ψ[φ]x.Therefore, [φ]ψx and[φ]¬ψx.Since x is maximal,¬[φ]ψ ∈ x and¬[φ]¬ψ ∈ x. Consequently,¬([φ]ψ∨[φ]¬ψ)∈x.Hence,using(A10),¬[φ](ψ∨¬ψ)∈x.Since x is consistent,[φ](ψ∨¬ψ)x.Since ψ∨¬ψ∈APAL,[φ](ψ∨¬ψ)∈APAL. Thus,[φ](ψ∨¬ψ)∈x:a contradiction. □

Lemma 9Let φ,ψ be formulas.For all maximal consistent theories x,〈φ〉ψ∈x iff φ∈x and ψ∈[φ]x.

Proof(⇒)Suppose〈φ〉ψ∈x.Hence,〈φ〉⊤∈x.Thus,using(A8),φ∈x.By Lemma 8,[φ]x is a maximal consistent theory.Suppose ψ[φ]x.Since[φ]x is maximal,¬ψ∈[φ]x.Therefore,[φ]¬ψ∈x.Consequently,¬〈φ〉ψ∈x.Since x is consistent,〈φ〉ψx:a contradiction.

(⇐)Suppose φ∈x and ψ∈[φ]x.By Lemma 8,[φ]x is a maximal consistent theory.Suppose〈φ〉ψx.Since x is maximal,¬〈φ〉ψ∈x.Hence,[φ]¬ψ∈x. Thus,¬ψ∈[φ]x.Since[φ]x is consistent,ψ[φ]x:a contradiction. □

Lemma 10Let φ be a formula and a∈Agt.For all theories x,if φ∈x,then Ka[φ]x=[φ]Kax.

ProofSuppose φ∈x.For all formulas ψ,the reader may easily verify that the following conditions are equivalent:

Definition 9(Canonical model)The canonical model Mc=(Wc,Rc,Vc)is defined as follows:

It will be clear that the canonical model is a model according to Definition 4.By Lemma 5,Wcis a non-empty set,and by Lemma 6 the binary relation Rc(a)is an equivalence relation on Wcfor each agent a.

6 Completeness

ThemainresultofthisSectionistheproofofAPAL’sTruthLemma(Lemma12). This proof is different from and simpler than the proof presented in[2].

Definition 10Let φ be a formula.Condition P(φ)is defined as follows:

for all maximal consistent theories x,φ∈x iff x∈‖φ‖Mc.

Condition H(φ)is defined as follows:

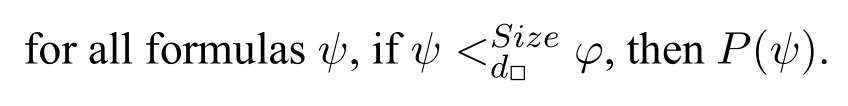
Our new proof of APAL’s Truth Lemma is done by using an-induction on formulas.More precisely,we will demonstrate that

Lemma 11For all formulas φ,if H(φ),then P(φ).

ProofSuppose H(φ).Let x be a maximal consistent theory.We consider the following 13 cases.

Caseφ=p.P(p)holds,as p∈x iff x∈‖p‖Mc,by the definition of the canonical model and the semantics of propositional atoms.

Caseφ= ⊥.P(⊥)holds,as⊥x and x‖⊥ ‖Mc,by the definition of the canonical model and the semantics of⊥.

Caseφ=¬ψ.The reader may easily verify that the following conditions are equivalent.Theinductionusingisusedbetweenstep2.andstep3.Asimilarinductive argument is also used in all following cases:

Caseφ= ψ∨χ.The reader may easily verify that the following conditions are equivalent:

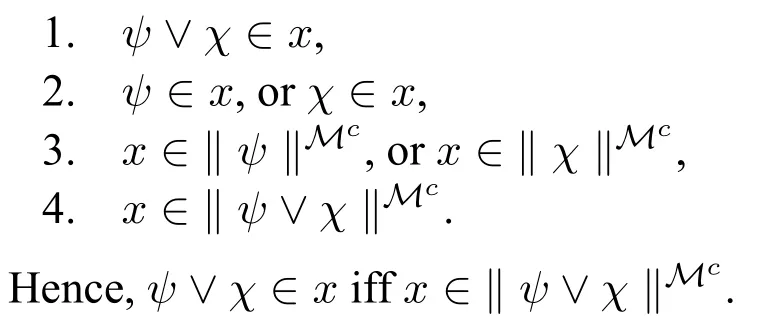
Caseφ =Kaψ.The reader may easily verify that the following conditions are equivalent.The implication from step 2.to step 1.is by Lemma 7.

Caseφ=[ψ]p.The reader may easily verify that the following conditions are equivalent.Between step 1.and step 2.,use axiom(A7)[ψ]p↔(ψ→p),so that[ψ]p∈x iff ψ→p∈x(similar justifications apply in the other cases of form[ψ]χ).

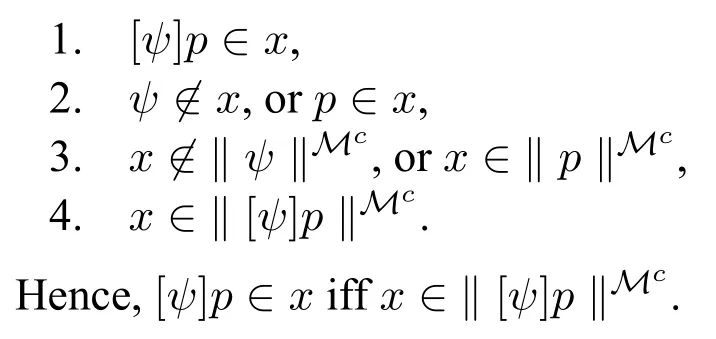
Caseφ =[ψ]⊥.The reader may easily verify that the following conditions are equivalent:

Caseφ=[ψ]¬χ.The reader may easily verify that the following conditions are equivalent.In the crucial equivalence between step 2.and 3.we use that¬[ψ]χ[ψ]¬χ,a consequence of Lemma 2(the d□depth is the same for both formulas).

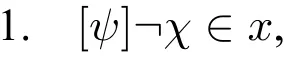
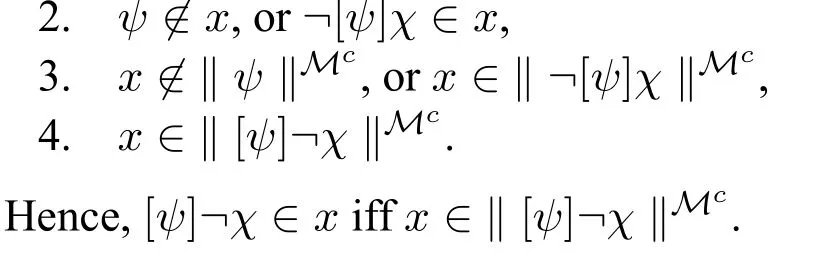
Case φ=[ψ](χ∨θ).The reader may easily verify that the following conditions are equivalent:

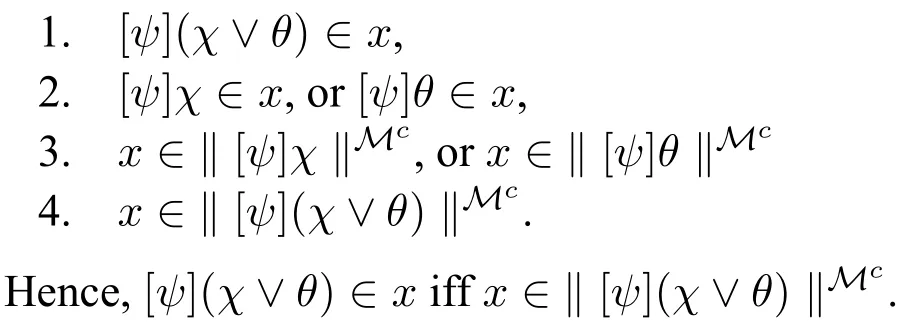
Case φ=[ψ]Kaχ.The reader may easily verify that the following conditions are equivalent(again,a crucial step is between 2.and 3.where we can use induction on Ka[ψ]χ because of Lemma 2):

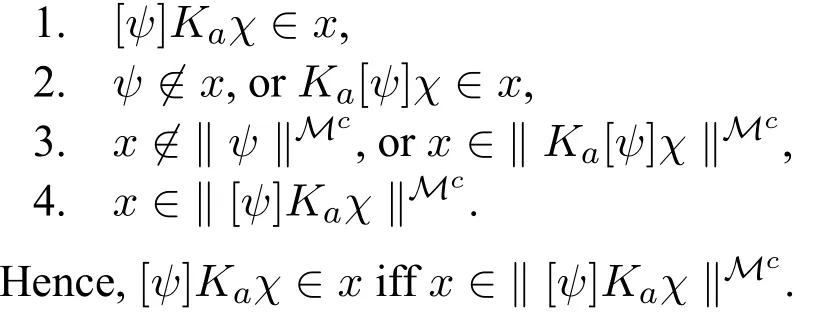
Caseφ=[ψ][χ]θ.The reader may easily verify that the following conditions are equivalent(and once more,a crucial step is between 2.and 3.where we use Lemma 2):

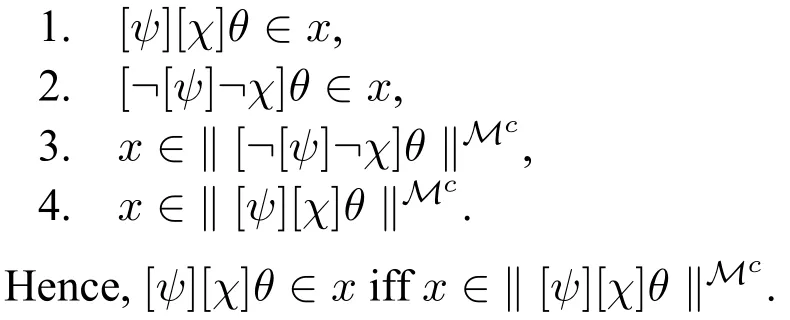
Caseφ=[ψ]□χ.The reader may easily verify that the following conditions are equivalent.Between 1.and 2.,we use derivation rule(R4)on the necessity form [ψ][θ]χ(i.e.,([ψ]♯)([θ]χ))and closure of maximal consistent sets under(R4).Between step 2.and step 3.we use the complexity measure,where we now simply observe that[ψ]□χ contains one□less than[ψ][θ]χ.Between step 3.and step 4.,we use the semantics of arbitrary announcements□and of announcements [ψ]:we note that x∈‖[ψ][θ]χ‖Mcis by the semantics equivalent to:x∈‖ψ‖Mcimplies x∈‖[θ]χ‖(Mc)ψ.

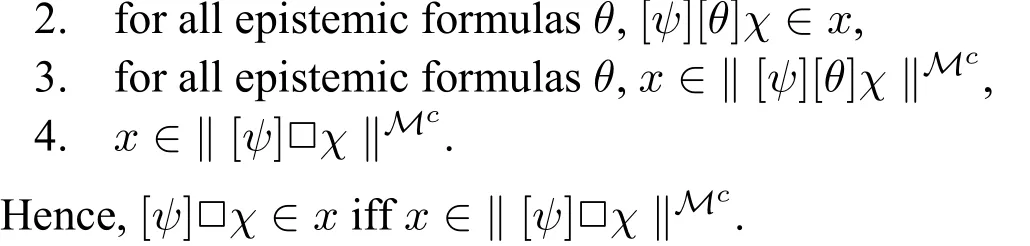
Caseφ=□ψ.The reader may easily verify that the following conditions are equivalent.The equivalence between step 2.and step 3.follows from the fact that for all epistemic formulas χ,[χ]ψ

Lemma 12(Truth Lemma)Let φ be a formula.For all maximal consistent theories x,

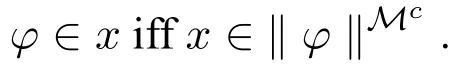
ProofBy Lemma 11,using the well-foundedness of the strict partial orderbetween formulas. □

Now,we are ready to prove the completeness of APAL.

Proposition 1For all formulas φ,if φ is valid,then φ∈APAL.

ProofSuppose φ is valid and φAPAL.By Lemmas 3,4 and 5,there exists a maximal consistent theory x containing¬φ.By Lemma 12,x∈‖¬φ‖Mc.Thus, x‖φ‖Mc.Therefore,‖φ‖McWc.Consequently,φ is not valid:a contradiction. □

7 Conclusion

Wehaveprovidedanalternative,simpler,completenessproofforthelogicAPAL. The proof is considered simpler,because in the crucial Truth Lemma we do not need to take finite sequences of announcements along.Instead,it can proceed byinduction on formulas.We consider this result useful,as the completeness proofs of various other logics employing arbitrary announcements or other forms of quantifiying over announcements may thus also be simplified,and as it may encourage the developments of novel logics with quantification over announcements.

References

[1] P.Balbiani,2015,“Putting right the wording and the proof of the Truth Lemma for APAL”,Manuscript.

[2] P.Balbiani,A.Baltag,H.van Ditmarsch,A.Herzig,T.Hoshi and T.D.Lima,2008,“‘Knowable’as‘Known after an announcement’”,Review of Symbolic Logic,1(3): 305-334.

[3] P.Balbiani and D.Vakarelov,2001,“Iteration-free PDL with intersection:A complete axiomatization”,Fundamenta Informaticæ,45:173-194.

[4] R.Goldblatt,1993,Mathematics of Modality,Stanford,California:CSLI Publications.

[5] D.Harel,1979,First-Order Dynamic Logic,New York:Springer-Verlag.

[6] M.Kaneko,T.Nagashima,N.-Y.Suzuki and Y.Tanaka,2002,“A map of common knowledge logics”,Studia Logica,71(1):57-86.

[7] J.Plaza,1989,“Logicsofpubliccommunications”,Proceedingsofthe4thISMIS,pp.201-216,Oak Ridge National Laboratory.

[8] V.Rybakov,1997,Admissibility of Logical Inference Rules,Amsterdam:Elsevier Science.

关于APAL完全性的一个简要证明

菲利普·鲍博尼
图卢兹大学法国国家科学研究中心信息研究所
philippe.balbiani@irit.fr

汉斯·范·狄马赫
洛林大学法国国家科学研究中心信息与计算机科学研究与应用实验室
hans.van-ditmarsch@loria.fr

鲍博尼等人（P.Balbiani et al.,[2]）提出了任意公开宣告逻辑（APAL）。它是普拉策（J.Plaza，[7]）公开宣告逻辑的扩展，加入了关于宣告的量词。这种逻辑已经被公理化，但它的完全性证明总被认为可能会很复杂。在本文中，我们提供了关于任意公开宣告逻辑的一个简要的完全性证明。这个证明是鲍博尼等人（[2]）证明的优化版。

Received 2014-10-15 Revision Received 2015-03-03

*We acknowledge useful discussions on the completeness of APAL with Jie Fan,Wiebe van der Hoek,and Barteld Kooi.Special thanks go to Jie Fan for careful reading of the manuscript and correctinganerror inthedefinition of the d□measure.Wethankthe reviewersofthe journalfortheir insightful comments and corrections.Hans van Ditmarsch is also affiliated to IMSc,Chennai,as research associate.He acknowledges support from ERC project EPS 313360.