Fanning the Flames of Reason: A Personal View of Logic

Johan van Benthem

Institute for Logic,Language&Computation,University of Amsterdam Departmennt of Philosophy,Stanford University Department of Philosophy,Tsinghua University

johan.vanbenthem@uva.nl

Fanning the Flames of Reason: A Personal View of Logic

Johan van Benthem*

Institute for Logic,Language&Computation,University of Amsterdam Departmennt of Philosophy,Stanford University Department of Philosophy,Tsinghua University

johan.vanbenthem@uva.nl

. Modern logic has the tools for becoming a broad science of reasoning and other information directed behavior that plays an important role in connecting the humanities,exact sciencesandsocialsciencesattheuniversity,andwhichispartofthebedrockofourinformation society.This paper is a revised version of a valedictory lecture delivered on 26 September 2014 as a University Professor of Pure and Applied Logic in the main auditorium of the University of Amsterdam.It traces the history of modern logic,illustrates the emergence of new trends in logic and agency,and discusses the most important future challenges facing it.

PII:1674-3202(2015)-01-0002-21

ArgumentsWhen people hear that you are a logician,their eyes start looking for the nearest exit.But now and then,there are creatures like me,whose encounter with logic changed their life.Already in high school,I liked rules and formulas,which I jotted down in a special notebook.And when I arrived at the UvA in its revolutionary 1960s,I loved to engage in argumentation about the future shape of Dutch societyto be determined of course by us,the student elite.My argumentative skills were not particularly successful,however,and I well remember the sinking feeling of slowly, but inexorably talking myself into a corner with an indefensible claim.A kind fellow student advised me to buy a book about logic,and that is what I did.1I add three pictures of what the species of logicians looked like to me at the time.The third picture is of my inspiring first teacher in Amsterdam,Else Barth.

Reasoning patternsWhat I bought was a pocket edition of a 19th century classic by William Stanley Jevons,available on the internet today.And what I learnt was that reasoning has patterns,and that some patterns are correct,while others are not.

To see this,consider the following statement,where the two capital letters stand for arbitrary sentences:

If B,then not-H,and ask yourself if it follows logically that

Chrysippos of Soli

W.Stanley Jevons

Else Barth

If not-B,then H.

You might be tempted to agree.But what if the doctor on duty in the emergency room where you have just been rushed in after a collapse,is trying to figure out what is wrong with you?Let us say that,if the cause is in your brain,it is not in your heart -but nothing is wrong with your brain scan.Is it correct to conclude that something isthematterwithyourheart?Idonotthinkso,andneithershouldyou.Iwouldprefer a doctor whose reasoning goes differently,using a correct reasoning pattern like this:

from“if B,then not-H”to“if H,then not-B”.

Of course there is more to proper diagnosis than just these few rules-but at least,on the lighter side,you now see that logical correctness may be a matter of life or death.

Explaining and teachingIn general,logical reasoning patterns lie behind how we find the truth,and explain it to others,and ourselves.I always felt a need to explain things I think I understood as a private test.As a student,I would walk at night in the Lairessestraat in Amsterdam talking to myself to explain what I had learnt from the day’s classes.Again,people around me quickened their step and increased their distance-and this time,even without my having told them that I was a logician.

Logic across culturesIn line with the thread of my own personal experiences,most of this lecture will follow the Western mainstream history of the discipline of logic. However,it is important to emphasize that a sensitivity to reasoning patterns and their valid laws is not a Western preoccupation:it is a talent that has occurred quite early across different cultures.Indeed,we live in exciting times where many new historical sources for our field are coming to light,as archives yield their secrets.Logic stands in a worldwide movement including ancient Greece,China,India,and the Islamic tradition,as shown in the efforts of a growing number of scholars today.

To complement the dominant facebook of the field shown earlier,I add some pictures of major logicians in these other cultural streams.One day,Mozi,Dignaga, and Ibn Sina may be names that are as familiar to the intellectual public as Aristotle.2With a group of dedicated colleagues,I am currently involved in exploring Chinese strands in all of this,in the forthcoming“Handbook of the History of Logical Thought in China”.

Reasoning and informationBut logic is more than seeing patterns and improving reasoning practice.With the study of correctness and incorrectness,we enter a much broader world of exact scientific ideas.One of these is the notion of information.

Mozi

Dignaga

Ibn Sina

In principle,there are precisely 4 ways the world might be like given the above statements B and H:

+B+H,+B-H,-B+H,-B-H.

If we then learn the above rule“if B,then not-H”,then we lose the possibility that +B+H.That is,we eliminate 1 out of the 4 options to obtain the information

+B-H,-B+H,-B-H.

If we now also learn the new fact that not-B,we lose the further possibility+B-H, but two still remain:

-B+H,-B-H.

This state does not have enough information to determine that H is the case.

You can check for yourself how this scenario of successive information updates differs from that for the logically valid inference pattern from“if B,then not-H”to“if H,then not-B”.Here the information does force the conclusion not-B through the following stages:

So,reasoning is tied up with information,the lubricant of our whole society,and logic suddenly starts looking like a much bigger field than you might have thought.

Logical systemsAnd there is still more than reasoning patterns and their underlying ideas.Quickly,I learnt that patterns form larger systems,that can be studied on their own intrinsic merits-all the way back to Aristotle’s system of syllogistic inference. Logical systems have mathematical structure,which leads to new avenues of its own.

Reasoning and computationThe criterion for correctness or incorrectness of simple rules like those I gave for implication and negation involves manipulating the‘truth tables’of basic logic,and thus reasoning gets tied to mathematical structures in computation.Thisisageneralthreadinthehistoryofideas:reasoningisconnectedto binary arithmetic,or as Hobbes said:“reasoning is reckoning”.And once we see this computational angle in its general light,the idea emerges naturally,as it did already in the Middle Ages,that reasoning might be done by machines,provided we find suitable logical languages for them to work with.The first picture below is Stanley Jevons’‘logical piano’,one of the pioneering attempts at creating mechanical computing devices.3Here I am not endorsing theold AI mantra that all reasoningcan be done by machines.The ultimate goal of logic to me is not a world where reasoning and judgment are left to technology,but one where we understand‘agency’,in the broad sense to come in this lecture.The second picture is Turing’s fundamental model of computation, and the third is an object that has swept the world in recent years.

There is a straight historical road from logic to computer science,and the information technology pervading our lives.

Logical Piano

Turing Machine

Macbook Air

This mixture of reasoning,information,and computation is the thriving conglomerate of logic,philosophy,mathematics,linguistics,and computer science that has put logic firmly at the crossroads of the modern university,and our modern information society.This,indeed,is the world of the Amsterdam Institute for Logic, Language and Computation where I have spent so much of my academic career.

The mathematical stance:logical systems and their theoryAs we have seen by now,logical patterns and systems capture major ideas that can be analyzed and developed as such.And the great engine for pursuing that analysis and development has been the mathematical turn of modern logic since the 19th century,turning it into an exact discipline that unleashes the power of mathematical precision to study systems of reasoning and everything that comes in their wake.This is how modern logic works,and nothing that I will say in the remainder of this lecture about broadening the scope of the discipline is intended to depart from this methodology.

Paradoxes,self-reflection,and foundational theoremsIn particular,the power of mathematical thinking allowed the great logicians of the 1930s to reflect on the basic nature of reasoning itself,both its strengths and its limitations.A celebrated instance ofthisstyleof‘confrontingreasonwithitself’,touseasonorousphilosophicalphrase, are Gödel’s Incompleteness Theorems that capture surprising essential features of the mathematical method par excellence,namely,deductive proof.

Consider one of the oldest instances of logical thinking that has come down to us invariouscultures,fromancientGreecetoancientChina,‘self-referential’statements that talk about themselves.A famous case is the Liar Paradox from Antiquity where someone asserts that the very statement she is making is false.But for here,think of a related but subtly different statement L that says about itself that it cannot be proved:

L if and only if L is not provable

or in Amsterdam-style formula notation4The strange box□is not a pdf conversion error,but the logical symbol for‘provability’.:

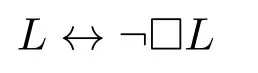
Languages have several ways of achievingsuchself-reference.Ifyouwantadramatic historical instance,the Hebrew God told the people seeking his essence:

“I am the unknowable one”.5Yes,there is much more to the‘unknowability’in this example than mere formal logic.

However,our logical intellect does not stop at such a statement,and the liar sentence L admits mathematical reasoning with startling consequences.

Here is a piece of this reasoning at the edge of reason.It is well within your capacities to appreciate-at least,assuming the famous motto of John Perry and Ken Taylor’s radio show Philosophy Talk:“the only thing that we do not question is the hearers’intelligence”.

Let us draw some quick consequences in a first,rather simple pass:

Gödel lite.

Is L true or false?If we assume that L is false,then L is provable.6Here we use earlier rules:we have¬□L→L by the meaning of L,and hence also¬L→□L.

But if L is provable,then L is true:and hence we have contradicted our original assumption.

We conclude from this episode that L cannot be false.

In other words:L is true.

But given what the proof-theoretic Liar L says,it follows that

L is a true statement that is unprovable.

The following pictures show some resounding names in this world of thought.

Euclid’s Elements

Gottlob Frege

Kurt Gödel

Martin Löb

Living at the edge of reasonThis simple piece of reasoning lies at the heart of Gödel’s famous First Incompleteness Theorem.But it is clearly just a very first pass, whichinvitesquestionsandrefinementatonce.Indeed,theartof‘livingdangerously’displayed here is another major attraction of logic,especially to minds of a somewhat absolutistbent,anditinvolvesacontinuouspracticeofrefiningourstylesofthinking.

To turn the screws of exactness a little bit more,how reasonable,really,was the above step where we assumed that provable statements L are true?Does not that represent an unwarranted confidence in the reliability of our proof methods?The greatlogiciansworkinginthefoundationsofmathematicsinthe1930ssuchasGödel, Hilbert and Gentzen thought so,and dropped this assumption in their analysis of the power of proof.Let me sketch a more sophisticated version for you then:

Assume we have□(L↔¬□L)(*).Next,assume that□L.Then using(*),we can prove that□¬□L.But at the same time,inspecting the proof for L that exists by□L,we can prove that□□L.Combining these two observations,a contradiction¬□L&□L is provable.So,our proof system is inconsistent,and unreliable.

Thistimeourconclusionabouttheedgeofreasongetsmoresophisticated.Ifour mathematical proof methods are reliable,then there have got to be true unprovable statements beyond their reach.

The process of refining our understanding of truth,proof,and reliability is still going on.Masters of the art included my thesis supervisor Martin Löb,Sergei Artemov,Dick de Jongh,and Albert Visser-and still last year,I read surprising delightful new perspectives on the mechanics of Gödel’s reasoning discovered by Lev Beklemishev at the Steklov Institute in Moscow.We can keep reflecting on our understanding of mathematical proof,and go deeper and deeper,until the mind reels.

Science,religion,or common sense?With all this,we are at the heart of classical logic and foundations of mathematics,and its deep results that keep inspiring religious awe in every new generation of students worldwide that gets exposed to logic. Yet,this depth comes with a somewhat narrow focus on mathematical proof,a very specialized human activity.The methods are mathematical,the topic is mathematics.

But I started this lecture in our daily reasoning practice,and want to return there eventually.Asastudent,Ihadtomemorizealistofdifferencesbetweenscientificand common sense reasoning-with the former supposed to be much deeper and better than the latter.But the striking thing to me is the very opposite.The logical steps for Gödel’s Theorem are the same ones that we employ in daily life,and this observation fitsthefactsofhumancognitiveevolution,wherebandsofhunterswithsurvivalskills eventually produced the greatest art and science,all using the same brain.

The true story of modern logic then is as follows.The methods remain mathematical,but the topic becomes much broader:in principle,any aspect of the human intellect.The truefacebook of logic,then,consists ofbothmathematiciansand others looking beyond,forming pairs as in the following pictures of contemporaries:

Frege

C.S.Peirce

Brouwer

Beth

Frege was contemporaneous with C.S.Peirce,an independent inventor of firstorder logic with a much broader agenda in philosophy,semiotics,psychology,and so on,which we are only beginning to carry out today.Our national mathematical icon L.E.J.Brouwer was a contemporary of E.W.Beth,a broad logician and philosopher, and it is their tandem that created the Dutch School in logic that we know today.It would be easy to multiply examples of such contemporaneous facebook pairs all over the history of logic.

So,here is where this lecture is going to go,charting further aspects of what our discipline is,or can become.Eventually,I want to understand the laws of what actual reasoning agents can and should do:in terms of knowledge,action,learning,making mistakes,and all of that in mutual social dependencies.And while setting our bounds that widely,I still hope to convince you that we are doing logic.

But before we enter this enticing Realm of Agency,let me first talk about the personal intellectual development that took me there.I will take things slowly,introducing new ideas one by one.

Proof as seeing and as doingI start with two essential aspects of mathematical proofs that have occurred entangled ever since Euclid’s“Elements”in Antiquity.A proof is evidence that a theorem is true:that is,it provides information-but at the same time,it is a method for computing solutions and creating situations where the theorem holds.The same duality pervades general learning and knowledge,where‘knowing that’and‘knowing how’are deeply intertwined.For instance,we have truly learnt a language,not just when we recognize when given sentences are correct, butarealsoabletoproducediscoursethatmakessense,andthesameistrueforlogical systems.Quite generally,studying information also means studying action,and vice versa.The two notions are two sides of the same coin.

How can logic do justice to this deep duality?

Reasoning about information and actionLogicians have long studied reasoning about both information and action-though they may come to these pursuits from different academic fields.Logical systems analysing information often come from the philosophical study of knowledge and belief,but in recent years they have entered computer science and economics.‘Dynamic logics’of action come from computer science,in the analysis of programs and processes,but have spread to philosophy and linguistics.These contacts have blossomed over the years,and taken their practitioners to Nobel Prizes,Turing Awards,or their equivalents in philosophy.The following four pictures present you with a gallery of relevant names and topics ranging from philosophy through computer science to game theory:

Hintikka

Dynamic Logic

Milner

Aumann

ModallogicTheabstractcommonstructureofinformationandactionthatunderlies large parts of philosophy,computer science,or game theory is studied in a technical field called modal logic.A modal notion states how things might be,insofar as not ruled out by our information-or how things might become,given the actions at our disposal.Very similar laws govern such notions.One example is this:

In terms of information,this principle expresses that

if I have evidence for A→B as well as evidence for A, then I also have evidence for B.7This use of the box notation is naturally related to our earlier formal analysis of provability.

In terms of actions,the same principle says that

if the outcomes of an action satisfy A→B,and also satisfy A, then all outcomes of that action satisfy B.

There are many other,and technically much more sophisticated,laws of modal logic, but the simple example of the Distribution Law will have to do here.8In particular,if the actions considered can be different,then Distribution must be modified to an indexed format[x](A→ B)→ ([y]A→ [x#y]B),where the variables x,y stand for actions and# denotes some suitable operation of combining actions.

Modal reasoning patterns have been a focus in my work over the years,which offers a systematic study of modal laws,but also of connections between modal patterns and other basic logical systems,measured by semantic invariances such as‘bisimulation’.Some sources are depicted in the sequence of four books below:

Dissertation

Monograph

Handbook

Textbook

These matters can be found in any good textbook,but let me stress one point. While modal logic is‘applied’as a theory of information and action,it is at the same time‘pure’as a formal theoretical study of basic aspects of reasoning that had not come to light before,and thus it falls squarely within the mathematical methodology that I have emphasized.9Modal logic is not the only field that does justice to the information-action duality.Other such paradigms that I admire include process algebra and category-theoretic approaches.

Information-driven agencyBut let us now move beyond the agenda stated so far. For a start,what about the actors getting the information and engaging in actions? What do they do,and why?My next step toward the study of agency is an arena where knowledge and action meet naturally,the basic informational acts themselves.

Basic informational actsWhile reasoning may seem the only informational action of interest to logicians,in reality,inference steps usually occur together with other equally fundamental acts that make information flow.For instance,the following scenario plays out day by day in Amsterdam cafés.

The Restaurant Three people order three drinks:water,beer,and wine.

A new waiter comes to the table carrying three glasses.There are 6 ways these drinks could be distributed,and here is what you will see happen.

The waiter asks who has the beer,say,and after hearing the answer,puts down that glass in the right place.This reduces his uncertainty from the initial 6 options to 2,muchasinourexampleofdiagnosticrules.Thewaiterthenasksasecondquestion, and puts,say,the glass of water.Now his options are down to 1,and he does not ask any more,but can infer who has the wine,putting it down without a question.

Thus,basic informational acts include,at least,both questions and inferences. But there is more to our basic abilities.As it happens,a broad view of informational action was already present with the ancient Chinese logicians in the Moist school,active from around 500 BC.It stressed the interplay of three sources that come together in producing information:

知 闻 说 亲 (zhi wen shuo qin)

an elegant compact statement which says roughly,in a more modern phrasing,that“knowledge comes from three sources:hearing from others,proof,or experience”.

Here the third category of‘experience’is one more major source of information, in daily life as well as in the natural sciences:namely just observing things.10TheMoistexamplewasaDarkRoom,withanobjectinsidewhosecoloryoudonotknow.However, you see a white object outside of the room,and someone now tells you that the object in the room has the same color.You then conclude that the object in the room is white.Observation is what a logical detective like Sherlock Holmes needs in addition to pure deduction,and it is the wellspring of the empirical sciences,on a par with mathematical proof.The next group of pictures represent a restaurant,a Moist dialogue, Sherlock Holmes at work,and finally,a card puzzle with social reasoning that is often used in my circles.

Logic of information changeMy own view of logic has come to resemble this ancient paradigm.We must study all basic informational acts on a par:inference, observation,and communication,and their interplay in how we deliberate,plan,and decide.A major test for such a venture is a search for formal laws governing these additional informational actions that retain the precision logicians are used to.

Here is one such law:

This law describes the new knowledge an agent i will possess after having received theinformationthatφisthecase.11These formulas are mainly for display:I ruthlessly omit technical details in this lecture.Just for once:the stated law describes knowledge after update as conditional knowledge in a recursive manner that lends itself well to logical analysis of the relevant modal reasoning.Itdoessointermsofthe‘conditionalknowledge’that the agent had before the new information!φ came in.Typically,it is‘recursion equations’like this law that drive the logical study of information-driven agency.

As an aside,please note how the above principles show an intimate cooperation ofideasfromdifferentfields:themodalityKiψ forknowledgeinthislawcomesfrom philosophical logic,while the dynamic modality[!φ]for action comes from logics of computation.

Still,we are only at the start of a logical study of agency.The actors in the above couldstill beinstinctivedevices recordinginformationfromtheenvironment,likethe bees sucking up nectar from the flowers in my garden.So let me turn to further basic intelligent activities that rational agents engage in,of which I will mention a few in this lecture.

Consistency?The first new aspect of agency concerns the quest for certainty we saw earlier.The founding fathers of modern logic were concerned with the power of proof,and its reliability.Is consistency our ultimate goal?Gottlob Frege thought so,saying that mathematics would‘crumble like a house of cards’if a contradiction were to arise.12In daily life we also value‘consistency’,a more subtle virtue of applying the same standards to similar matters,without self-serving shifts,a delicate form of harmony in judgement.But this seems excessive timidity:there can be logical grandeur in fragility,being wrong,and a volte face.

Learning is correctionAs I said before,proofs give reasons,and a rational agent can be described as someone driven by reasons.13The common idea that rationality means‘serving one’s own interests’seems an aberration.Good reasons involve much more,such as an ability to put oneself in someone else’s place.But at this point,I part company with the original foundational enterprise.Our drivers should be good reasons-but thereisnoguaranteethattheyarecorrect.Wemakemistakesandoftenformincorrect beliefs,andthetaskoflogiccannotbetopreventthatfromhappeningonceandforall. Indeed,our beliefs and expectations,even when wrong,represent a creative human talent in navigating a world where knowledge is a currency that is often unavailable.

But this non-eliminable,and perhaps even desirable,potential for error comes with another creative talent,our ability to correct ourselves when beliefs are shown wrong by an observation,or when theories explode after a contradiction comes to light.There is no house of cards that crumbles:indeed,human intelligence shows at its finest in a clever recovery after we have been shown incorrect.So,a true logic of rational agency tolerates errors and highlights methods for revising beliefs.What this points at more generally is an intimate connection between reasoning and learning.

While all this may be true,are beliefs and their revision a fit theme for logic? As it happens,thanks to the work of pioneers like Peter Gärdenfors,we know that this more delicate error-tolerant process of adjusting to new information still satisfies logical laws,that now involve operators for belief and acts of belief revision.Of such laws,I just display two at this point,to show you that,once again,we need not sacrifice the mathematical precision of our foundationalist founding fathers:

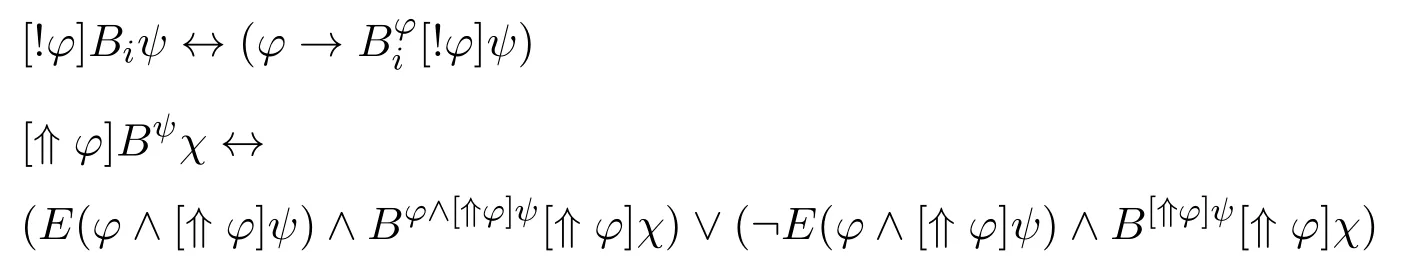
Such laws describe which new beliefs arise as new information comes in.This can now happen in two forms:witness the syntax of our two formulas.Changes can be triggered by a‘hard’totally reliable event!φ removing all¬φ-situations for good, but there is also a more‘soft’plausibility-changing event⇑φ that keeps all situations, while putting those with¬φ on top of those with φ.I am not going to try to explain to you any further what the above formulas say.Their typography may well scare you. These laws of learning are clearly more complex than the simple rules of reasoning that I started with.But then I never said that our broader logical skills are simple!

Let me just state the upshot.Correctness forms a tandem with correction-and as some philosophers have said long ago,logic is also about learning from errors.14This tandem view again illustrates the earlier point of the duality of information and action.

My favourite analogy for this comes again from health.Creating a World free from disease seems a sterile and unappealing goal:much more impressive is the dy-namics of the human immune system that deals with challenges as they occur.To me, logic is not the guardian of consistency proofs,but rather,

‘logic is the immune system of the mind’.15Students ask why I still grade exams for correct answers,instead of their responses to their errors. For lack of a good answer,let me just step aside,and say that exams are an ancient Chinese invention that has conquered the world,on a par with paper,gunpowder,and silk.

In terms of our initial example,maybe logicians themselves are doctors of the mind.

Evenso,Ishouldnotplayupthedifferencewithfoundationalresearchtoomuch. There might well be very interesting extensions of the classical theorems by Gödel or Turing when,in addition to what is known with total certainty,we also explicitly represent agent’s reason-based,but fallible beliefs about what is true and provable.16E.g.,while it might be provably inconsistent to know that a given statement is true and unknowable, it could well be consistent for an agent to believe that it has these two properties.Technical examples are found in recent work on probabilistic versions of Gödel’s theorems.

Many minds and social interactionBeliefs may need correction for all three reasons in the earlier picture of information dynamics:a surprising observation,a paradoxical inference,or also,being contradicted by somebody else.This leads me to my next fundamental theme in the logical study of agency,which can be summarized as:

“intelligence seldom comes alone”.

My example of argumentation was a socialscenario where different agents interact.This is significant.Rational behavior is a many-mind talent rather than an isolated skill-just as in modern science,the key is many-body interactions,not single bodies in their natural place,as in Aristotle’s physics.This social theme of deliberation and argumentation runs throughout the history of logic,in both Greek and Non-Western traditions.Logicisalsoabouthowweconvince,refute,orotherwiseinfluenceothers.

Just as earlier,this social dimension has two dual aspects that need to be studied together:information,and action.

Theory of mindThe social aspect of information involves a crucial human ability often called‘Theory of Mind’where we reason about the facts,but also about other people’s information,what they know about the facts and about us,and so on.Theory of Mind underlies many of our basic informational acts.My asking you a question normally conveys I do not know the answer,and also that I believe you might know the answer.17Ofcourse,bothofthesepresuppositionsareswitchedoffwhenateacherasksaquestiontoastudent, or a valedictory lecturer to his audience.

Social behavior is kept in place by a web of such complex iterated information about others that can be studied as before.Again,it has been found that crucial properties of rational social equilibrium then show up in logical laws.For instance,aproposition φ is‘common knowledge’in a group of agents G,i.e.,it is known up to any depth of iteration(written as CGφ),if and only if the following equivalence holds

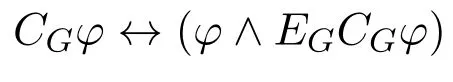
where an operator EGψ says that everybody in the group G knows that ψ is the case. This looks like a vicious circle that foolishly tries to define common knowledge CGφ in terms of that notion itself,but in fact,the above equivalence is a‘luscious circle’where the notion at issue is well-defined,and supports precise reasoning.18In mathematical terms,logical laws like this are‘fixed-point equations’.19The status of common knowledge is widely debated:it may just represent a useful fiction.

The program of logical dynamicsThe preceding samples suggest a systematic logical study of information-driven social agency.Over the past decades it has become clear that the methods of logic are well up to this agenda extension,creating systems with beautiful laws,not just for inferences,but also observations,questions,correction,learning,and social interaction.And in doing so,the grand style of our founding fathers does not lose its luster.Its thinking about strengths and limitations also applies to what diverse sources of information do for rational agents.In what follows,I discuss one current highlight of this‘Logical Dynamics’program,as exemplified in the depicted three books,from 1996,2011,and 2014,respectively.

GamesSocial action is at the heart of the fast-developing area of logic and strategic behavior in games.Our actions toward each other congregate to form longer-term strategies,where what I choose to do next depends on what you do now,and so on. Forexamplesclosetologic,justthinkofthetimingofplayingyourcardsinargumentation,or your points in giving a valedictory lecture.The logical laws of strategies or plans form a natural continuation of the earlier-mentioned logics of actions,and they often concern situations where strategies are in some sort of rational equilibrium, meaning that no agent has an incentive for deviating from her current plan.

Only one such law will have to serve as an example here,again mostly just in display.It is very similar qua form to the earlier equivalence for common knowledge,and it describes when someone has a strategy for playing a game G that alwaysachieves the effect φ(this is written here as{G∗}φ)in terms of φ’s being true and what the player can achieve by her currently available moves(the latter ability is written as{G}):

The analogy with the earlier law for knowledge again shows the fundamental duality of information and action that governs logic of agency.They are two sides of the same coin,and often,the shape of their mathematical laws reflects their similarities.

Harmony of information and desireHowever,in the fundamental notion of gametheoretic equilibrium in behavior between different agents,a new feature comes in sight that you might have thought far outside of the province of logic,namely,our preferences,intentions,and desires.We are not purely informational agents attuned to how the world is by knowledge or belief:everything we do is colored by what we want,hope,fear,or regret.While some people view the latter as a realm of blind impulses and irrationality,nothing could be further from the truth.What we want to know explains how we seek information,and what we want to achieve determines our choices of actions.Instead of a separating barrier between these two realms,a logical perspective on rationality involves understanding their delicate balance.20Public audiences often say to me that emotion rules the world,not logic.My response is finding lipstick on the collar of your spouse:observation,inference,and emotion entangle in a flash.21I sometimes wonder whether this balance also explains why mathematicians keep using natural language in their work and publications,be it enriched with symbols.It has often been asked why this is so.One answer might be that even pure mathematical research requires a constant undercurrent of signals for cooperation,competition,goals,and desires.

A reasonable person keeps her information in harmony with her goals and desires,plus those of others.That quality shows in the activity of taking decisions, a human ability that is of growing interest among logicians.Incidentally,it is that broader balance of information,desires,and decisions that we should also seek to instill in a true academic education.

Logic in gamesNoble causes indeed,but can logic offer any illumination in such a broad arena?What I can say for now is found in my new book“Logic in Games”.It covers two major lines of research,that have been developing over the past decades.

The first line is logic of games,being the study of the structure of games and everything that happens before,during and after their play by rational agents.There is a lot of intricate reasoning involved in plotting one’s course in games,including the effects of one’s actions,beliefs,preferences,and thinking about the kind of opponent (or fellow player)one is engaging with.This reasoning shows logical patterns that can be studied by the tools I have outlined in the above,including fixed-point laws for social equilibria where all players do the best they can.This line of research may be considered a joint offspring of logic,game theory,and modern computer sciencein its interactive-systems mode.Logic of games is now engendering a joint research programthatmightcalled‘TheoryofPlay’,whereweanalyzethereasoningofplayers ingamesandrelatedsocialscenarios-andsometimes,moreambitiously,trytodesign new games that implement desirable forms of social interaction.

But at the same time,there is a second intimate connection here,that may be called logic as games.As we have hinted at in the beginning of this lecture,paradigmatic logical phenomena such as argumentation themselves have a game-like character,and this metaphor can be made very precise.For instance,mathematical proofs have turned out to be very much like‘winning strategies’in suitably defined dialogue games.This game-theoretic view of logic itself also fits very naturally with modern views of computation,where the mathematical paradigm is no longer isolated Turing machines,but networks of distributed processors that may cooperate or compete for available resources,and that may differ widely in their abilities and intentions.

Thus,once more,logical laws acquire the dual character we have seen several times in this article.Viewed in an informational perspective,they tell us what the worldislike.Butinadualdynamicproceduralperspective,theyexpressfundamental facts about strategies and equilibria in basic scenarios of interactive computation or social behavior.This duality is not an annoying ambiguity,but rather the true face of logic as I see it.

The first two pictures here are lecture notes and a monograph of mine on both of the above interfaces of logic and games.The third picture is of a forthcoming book on logics for strategic reasoning,bringing together many communities,that I have edited with Sujata Ghosh and Rineke Verbrugge.This area is in full development.

What is next?Ladies and gentlemen,I have shown you glimpses and glimmers of my dynamic program for logic as a broad study of information-driven social agency. As one of my readers put it nicely:“classical logic handled the straight lines,now you want logic to also do the curves”.Many of those curves are found in my own work and that of my colleagues and students.What is left for me to do?

The empirical factsInmy declining years,I sometimes stray from the glorious path of theory,and feel the pull of the brute facts.What I told you about information andagencycanbeseenastheory-boundandnormative:thisistheinformationthatistruly available in the world,these are the conclusions that agents should draw,these are the game-theoretic equilibria they should attain.In this classical perspective,the laws of logical dynamics have no descriptive content,and how people really act,presumably stupid and ill-mannered,can be left to cognitive or behavioral scientists.

But I fear that this cozy analytic separation of the normative and descriptive reflects intellectual poverty rather than safety.Logical theory that ignores actual cognitive behavior seems dangerously empty,lacking focus.On the other hand,I do not want to lose the potential of normative thinking either,that can help us improve performance,or design better ways of dealing with the world and with one another. For instance,my earlier emphasis on correction rather than guaranteed correctness of intelligent behavior mixes these two motives.It moves closer to real human behavior, but what we call successful‘correction’will still depend on norms.In other words, things are subtle and complex here,and I have no definitive line to offer.22This has not prevented me from publishing papers on the interface of logic and psychology,a fascinating border region where much is happening,also at the University of Amsterdam.

Let me give an example where these two pressures in my current life come to a head.You might feel that my broad program for logic is becoming a huge machinery of high mathematical complexity.Now there is a mathematical unity in logical methods that makes this complexity less daunting.But it is also good to realize that you are in fact good at everything that I have discussed in this lecture.Information flow,inference,correction,desires,and strategic behavior occur together in that basic phenomenon that we all engage in all the time:conversation.Therefore,a natural empirical focus for my view of logic is natural language,the vehicle of conversation.

NaturallanguagesandrealbrainsInthe1980s,Iwasdeeplyengagedinthelogical analysis of natural language,and people sometimes ask where this love has gone.My work then was driven by static perspectives on language as reflecting the world,with hardly a trace of dynamic agency.But natural language is a major interface where logical intuitions meet empirical facts.

One project on my desk is the language of agency,studied in ways that will be familiar to you after my discussion of logic and games.One prong is a study of the patterns of agency that constitute language use,the other prong is the‘language of agency’,and all the subtle ways that we use for describing what we do,plus the laws of the natural logic governing this natural language.23More concretely,I am currently looking at simple reasoning patterns concerning the main drivers of our actions:hope,and fear-as well as what are in fact major cognitive abilities such as switching perspectives in going from first-person to third-person reports,and back.Throughout,the fundamental logical harmony of information and action reveals itself.At the same time,I am involvedwithempiricalresearchonlanguageinthebraininournationalGravityProject“Language in Interaction”where we will use logic-related games to see what reallyhappens when people communicate,and how new language arises in that process.

The four pictures displayed here show some of my earlier work on logic and natural language in the 1980s and 1990s,a Handbook on this interface,and a logo for the new project that also brings in a wealth of facts from empirical cognitive science.

Large numbers and probabilityThe second project waiting on my desk concerns another aspect of the facts,namely,that there are so many of them.Logical reasoning and rational agency play in a thin zone of conscious deliberation where what we think and decide matters.This zone is like the thin realm of our physical abilities,hemmed inbetweenobjectsthataretoolarge,ortoosmall,forourhandstomanipulate.Above us lies the statistical world of social behavior and public opinion,where each of our well-considered views is just a drop in the ocean.Below us is the statistical neural machinery of our brains,busily clicking away as an audience is listening to a speaker, but not under one’s conscious control.Here logic meets probability theory,as two major mathematical paradigms with different views of what are relevant patterns. My own interest in this area today concerns interfaces between logical and dynamical systemstheoryasprovidingtwoviewsoftheseinterfaces.Therearemanymoregood reasons for combining logic and probability,but the above may suffice for here.

The interface of logic and probability has a long history:even Stanley Jevons includeditinhisbookmentionedatthebeginningofthislecture..Itisalsoverymuch in evidence at our institute the ILLC,and I believe that it poses many fundamental problems that go far beyond what we know so far.

FoundationalresultsafterallFactualinterestsarebynomeansopposedtotheclassicalmodusoperandiinlogic.Someneuroscienceintriguinglyrepeatsidealsfromthe foundations of mathematics,such as a‘Universal Scanner’that tells us exactly what an experimental subject is thinking,a goal with a sinister whiff of Inquisition.Fortunately,one can modify famous arguments in logic to show that universal scanners are as impossible as universal decision methods for reasoning or computation.

Spreading the word in educationThe best test of a proposed scientific perspective may not be whether it pleases one’s senior colleagues,but whether it is teachable to audiences with fresh open minds,such as students,or the general public.

I wish I could jump right into things here and start teaching you the topics of this lecture,but there are other resources for that,such as our on-line course Logic in Action:www.logicinaction.org

I recommend a tour of this educational world,which we are still creating and testing out at several sites worldwide,including Amsterdam,Stanford,Beijing,and Seville.The following pictures illustrate part of this world,as well as its outliers into the Open University and on-line education efforts at several pre-university stages.

This reflects the earlier ties between logic and learning.People can get better at argumentation,andmanyotherthemesinthis lecturepointatskillsthatcan betaught.

What is logic?Let me return to the beginning of this lecture.What subject did I choose as a student,and was it the right choice?My general view of decision is quite unlike the paradigm in decision theory of choosing optimal actions given one’s present expectations.This is too passive.In my own life,decisions turned out to be good,not because of superior a priori reasoning,but because I made them good afterwards by committing to the actions that I had taken.This views also holds true for choosing logic.

Perhaps the field as it was when I chose it in the 1960s was not an optimal choice for someone like me.24My sons occasionally wonder if I would not have made a much more productive member of Dutch society as a physicist,the field of study that I started with at the UvA.But I have told you what logic can become if we take it to its full potential as a science of information in action,performed by agents engaged in meaningful activities,doing justice to both the classical ideals and a modern future of the field.Indeed,this view is at the heart of my Logical Dynamics program:

becoming is as important as being.

Deep thoughts and noble sentiments:but at the end of this long lecture,you may well prefer a lighter take home message.Let me try.Throughout my presentation,I have extolled the virtues of reason,as the light that,sometimes,relieves the boredomand darkness that can be found all around us.But that light has to come at the right time,in the right style.

One autumn night,fifteen years ago,I had a heart to heart conversation with my 85-year-old mother-and I put the question I had never dared ask before:why she had ever decided to marry my father.Her response was this:

“because you were not there to advise against it”.

There is a logical paradox lurking here,not unlike the ones I discussed in this lecture -but my mother’s response also gives me my final definition of logic for you today:

logic is the science of wit.

People and institutionsIn line with what I have said about logic and probability,my own views and life’s decisions have ridden on a statistical sea of behavior by many others.My formative interactions have included many colleagues and students,so much so,that I often wonder where my own professional persona ends and theirs starts.My work and ambitions in academic life also naturally led to helping shape new organizations in our field whose lifespan may well exceed our own.

The four pictures here show my habitats over the years:the Institute for Logic, Language and Computation in Amsterdam,the European Association for Logic,LanguageandInformation,theCenterfortheStudyofLanguageandInformationatStanford,andasamostrecentinitiative,anewJointResearchCenterinLogicbetweenthe UvA and Tsinghua University in Beijing.25Perhaps not accidentally,counting time zones,this is a realm where the sun never sets.These are academic sites where modern logic in the style I have explained is flourishing,as well as much more.But the realm of logic is much larger than this personal environment.I warmly invite you to open a door into the actual international world of logicians-or just at home,step through Alice’s mirror into the internet,and see its attractions for yourself.

烧旺理性的火焰：对逻辑的个人体会

范丙申
阿姆斯特丹大学逻辑、语言与认知研究所
斯坦福大学哲学系
清华大学哲学系
johan.vanbenthem@uva.nl

现代逻辑拥有一套方法，使得它能够成为关于推理和其他信息导向之行为的一门广泛的科学，不但在大学里起着联接人文学、精密科学和社会科学的重要作用，并且也是我们信息社会基础的一部分。这篇文章，是我2014年9月26号在阿姆斯特丹大学大礼堂里所做的“纯粹与应用逻辑的顶级讲座教授”（University Professor of Pure and Applied Logic）讲席之离职演说的修改版本。此文回顾了现代逻辑的历史，阐述了逻辑与智能主体领域里新出现的动向，并讨论了它在未来所面临的的最重要的挑战。范丙申目前是阿姆斯特丹大学逻辑学荣誉教授，斯坦福大学亨利沃尔格瑞夫斯图尔特哲学教授，同时也是清华大学长江学者奖励计划讲座教授。

Received 2015-01-24

*Johan van Benthem is a university emeritus professor of logic in University of Amsterdam,Henry Waldgrave Stuart Professor of philosophy in Stanford University and Changjiang Professor of philosophy in Tsinghua University.