相干逻辑关系语义的推理解释*,†

周北海

北京大学哲学系

zhoubh@phil.pku.edu.cn

贾青

中国社会科学院哲学研究所

v100jq@163.com

相干逻辑关系语义的推理解释*,†

周北海

北京大学哲学系

zhoubh@phil.pku.edu.cn

贾青

中国社会科学院哲学研究所

v100jq@163.com

关系语义是相干逻辑中最为重要的语义学之一，但是关系语义一开始就以“纯粹”的形式语义的面貌出现，其中三元关系R的直观意思是什么并不清楚，于是出现了关于关系语义的多种解释。我们认为，R所代表的是推理规则集、前提集和结论集三者之间的关系，据此提出了推理语义。推理语义以推理的形式结构为背景，有明确的直观意义。本文以相干逻辑系统R+为例，证明出推理语义是与关系语义等价的语义。从推理语义与关系语义的这个等价关系上看，推理语义完全可以作为对于关系语义直观解释的一个中间环节。由此不仅使得关系语义有了推理结构的解释，同时说明了相干逻辑是一种关于推理的逻辑。这与相干逻辑产生的历史也完全吻合。

相干逻辑；关系语义；推理语义

上世纪七十年代初R.Routley和R.Meyer给出了相干逻辑的关系语义（relational semantics）。这一语义中的框架是一个四元组〈K,R,0,∗〉，其中R是一个三元关系（[10-12]）。在关系语义下可以得到一系列相干逻辑系统的完全性，从这个角度看关系语义是一个成功的语义，因而成为了相干逻辑中最为重要的语义学。但是，关系语义一开始就以“纯粹”的形式语义面貌出现，其中三元关系R的直观意思是什么并不清楚，于是出现了关于关系语义，特别是R的多种解释。我们认为，R代表的是推理规则集、前提集和结论集三者之间的关系。基于这一理解，周北海（[15]）构造了推理模型并提出了推理语义（inference semantics）而且使用推理语义证明了一度衍推系统Efde的完全性。周北海（[16]）对此做了进一步的分析和讨论，讨论了推理语义与关系语义的一般性关系，但是没有具体说明推理语义如何用于相干逻辑。本文以相干逻辑系统R+为例，在给出R+推理语义模型的基础上，证明R+的推理语义和关系语义是等价的，从而进一步说明对于关系语义中的三元关系R做推理的解释是合理的，这一语义实际上是关于推理结构的刻画。

1 相干蕴涵与推理语义的直观解释

相干逻辑是以相干蕴涵（relevance implication）为核心概念建立的逻辑。相干蕴涵提出的动因是为了消除实质蕴涵悖论。相干蕴涵要求蕴涵式的前件和后件要有共同的命题变元（即相干原则），试图通过这一方法加强前后件的联系，以给出对日常推理中的推出关系更合理的刻画。

相干蕴涵是相干逻辑的核心概念，与此相应，关于相干蕴涵的语义解释也是相干逻辑关系语义的核心。设〈K,R,0,∗〉是一个关系语义框架，A→B是一个相干蕴涵式。对于任意的a∈K，A→B在a上为真，当且仅当，对于K中任意的b,c，如果Rabc且A在b中为真，那么B在c中为真。0是K中一个特别的元素，所有在0上为真的公式就是在这个框架形成的模型中有效的公式。这些就是关系语义的核心部分。但这还只是一个抽象的语义，因为其中并没有说明a,b,c都是什么，R又是什么意义上的关系，至多只是说到0是一个“逻辑建构”（logical set-up），什么是逻辑建构，对此没有更多的解释。正因为如此，于是引出了多种直观解释。对此我们认为，这个框架实际上也可以做推理的解释。

任何一个推理都有三个部分：规则、前提和结论。设A→B是一个推理规则。如果有前提A，那么经由规则A→B的应用就能得到结论B。一般地，设r是一个规则集，a是一个前提集，b是由r和a得到的结论集，即由r中的规则和a中的前提得到结论都在b之中，于是我们可以得一个三元组〈r,a,b〉。考虑到r可作用于不同的前提集以得到不同的结论集，于是有不同的三元组，如〈r,a′,b′〉，〈r,a′,b′〉等，进而形成一个三元组的集合{〈r,a,b〉,〈r,a′,b′〉,〈r,a′,b′〉,〈r,a′′,b′′〉,...}，这就是三元关系R。从这个角度看，R就是一种推理关系。

根据这个考虑，令Z是一个由公式集构成的集合，R是上述三元关系。于是，对于Z中任意的元素a,b,c,Rabc表示的是规则集a、前提集b和结论集c三者之间所具有推出关系。在此基础上，还可以设一个特殊的规则集，称为逻辑规则集，记作r。Rrab与Rabc类似，只是其中的规则集r是逻辑规则集。这里的“逻辑规则”即适用于Z中的所有公式集的规则。于是，可以通过由Z，R，r三个要素组成的三元组〈Z,R,r〉作为语义装置，用以刻画推理的形式规律。设G是一定条件下所有这些三元组构成的集合，令LG=∩{r|〈Z,R,r〉∈G}。于是，LG中的公式就是由G所确定的所有推理都适用的规则，从而达到对于某种逻辑的刻画。

三元组〈Z,R,r〉通过规则集（包括逻辑规则集）和前提集以及结论集之间的关系表达了推理的最为基本的结构。因此这个语义称为推理语义。规则集、前提集和结论集是所有推理最一般的组成要素，由此得到推理的一般形式结构。在这个基础上，还可以考虑不同类型的推理，增加一定的条件，由此得到不同逻辑。周北海（[15]）用推理语义证明了Efde的可靠性和完全性。本文试以相干逻辑系统R+为例，将推理语义推广到相干逻辑。重点是考察推理语义与关系语义之间的等价关系。推理语义有明确的直观背景，可以通过这个等价关系给出关系语义的直观解释。

2 相干逻辑系统R+及其关系语义

系统R+（[1]）是相干逻辑的重要系统之一，是最集中体现相干蕴涵性质的纯蕴涵系统R→的扩张，并且具有一定的简洁性，比如不用考虑否定联结词，可以使得语义框架、模型相对简单（省去否定算子∗），以更集中地讨论目前的主要问题。

R+的语言记作L，其中有可数多个命题变项p,q,...，连接词→,∧,∨，以及左括号“(”和右括号“)”；有以下类型的公式：变项，A∧B，A∨B和A→B。以下用V(L)表示L的变项集，F(L)表示L的公式集。

R+的公理模式和规则：

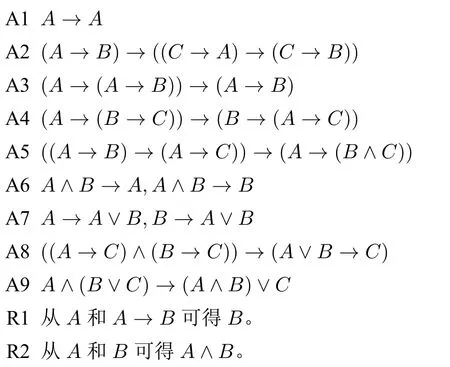
定义1三元组〈K,0,R〉是一个R+框架，当且仅当，

(1)K是一个非空集，其中的元素称为建构（set-up）；

(2)0∈K，称为逻辑建构；

(3)R是K上满足以下条件的三元关系：对任意的a,a′,b,c∈K，1这些条件因为依赖关系与原文的排序有所不同（详情见命题2）。

(i)同一性（Identity）：R0aa；

(ii) 幂等性（Idempotence）：Raaa；

(iii)交换性（Commutativity）：Rabc⇒Rbac；

(iv)结合性（Associativity）：R2(ab)cd⇒R2a(bc)d；2R2(ab)cd=df∃x(Rabx∧;Rxcd)，R2a(bc)d=df∃x(Raxd∧Rbcx)。

(v) 单调性（Monotony）：Rabc且R0a′a⇒Ra′bc。

定义2结构M=〈K,0,R,⊨〉是一个R+模型，当且仅当，

(1)〈K,0,R〉是R+框架；

(2)⊨是一个从K到F(L)的关系（称为赋值关系），满足下面的条件：

(i)对任意的变项p，如果M,a⊨p并且R0ab，则M,b⊨p；

(ii)M,a⊨A∧B，当且仅当，M,a⊨A且M,a⊨B；

(iii)M,a⊨A∨B，当且仅当，M,a⊨A或M,a⊨B；

(iv)M,a⊨A→ B，当且仅当，对任意的b,c∈K，如果Rabc且M,b⊨A，那么M,c⊨B。

定义3设M是任意R+模型，A是任意公式。如果M,0⊨A，那么A在M上被验证（verified）；如果A在所有模型上都被验证，那么A是有效的。

在这一语义中，R+是可靠的和完全的（[2,6]）。

3 R+的推理语义

每一推理都包括规则集、前提集和结论集三个部分。以下所给出的就是根据这个思想所构建的R+形式语义，其中也参照了R+的关系语义的特点。

记号设a,b是任意的公式集，令[ab]={B|A→B∈a且A∈b}。

定义4三元组〈Z,R,r〉是一个推理语义框架，当且仅当，

(1)Z⊆℘(F(L))；

(2)r∈Z，称为逻辑规则集；

(3)对任意的a,b,c∈Z，Rabc，当且仅当，[ab]⊆c。3这是Rabc的严格表述。确切的说，[ab]是由规则集a和前提集b得到的结论集。Rabc即[ab]包含于c。c是包含[ab]的集合，为表述方便也简称结论集。

定义5四元组M=〈Z,R,r,⊩〉是一个推理语义的模型，当且仅当，

(1)〈Z,R,r〉是推理语义框架；

(2)⊩是一个从Z到F(L)的关系（称为赋值关系），满足下面的条件：

(i)M,a⊩p，当且仅当，p∈a；

(ii)M,a⊩A∧B，当且仅当，M,a⊩A且M,a⊩B；

(iii)M,a⊩A∨B，当且仅当，M,a⊩A或M,a⊩B；

(iv)M,a⊩A→ B，当且仅当，对任意的b,c∈Z，如果Rabc且M,b⊩A，那么M,c⊩B。

定义6三元组〈Z,R,r〉是一个R+的推理语义框架，当且仅当，

(1)〈Z,R,r〉是推理语义框架；

(2)Th(R+)⊆r；

(3)对任意的a,b,c∈Z，任意的A,B∈F(L)，

(i)[ra]⊆a；

(ii)[aa]⊆a（a对分离封闭）；

(iii)[ba]⊆[ab]；

(iv)[a[bc]]⊆[[ab]c]；

(v)[ra′]⊆a⇒[a′b]⊆[ab]。

定义7四元组〈Z,R,r,⊩〉是R+的推理语义模型，当且仅当，

(1)〈Z,R,r〉是一个R+的推理语义框架；

(2)⊩推理语义模型中的赋值关系。

定义8设M是任意R+推理语义模型的模型类，A是任意公式。A在M上有效，当且仅当，对于任意模型〈Z,R,r⊩〉∈M，A∈r。

R+的推理模型是存在的。这可以通过下面的例子来证明。

设Z′={r,a,b,c,d,e}。其中r=Th(R+)∪{p,q,r,s,p→q},a={p,q,r, p∧q→q,p→q},b={r,s,r→r∨p},c={p,q,p→q,q→q}，d={q,s,q→q}，e={q,q→q}。

设x是Z′中的任意公式集，令x是满足以下条件的最小集合：x⊆x且对R1和R2封闭并对规则“从A或B得到A∨B”封闭。令Z={r,a,b,c,d,e}。根据定义7，可以验证〈Z,R,r〉是一个R+框架，于是，〈Z,R,r,⊩〉是一个R+模型。

定义7以R+为例，给出了完整的推理语义。根据这个语义，所有有效公式形成一个公式集，记作LR+。从R+的推理模型看，LR+中的规则普遍适用于一定条件（即定义6给出的框架条件）下的所有推理，而且LR+包含了所有这样的规则。如果可以证明R+对于这个有效公式集是可靠的和完全的，那么可以说，R+是LR+的公理化系统。事实上，这个推理语义也是根据R+的关系语义给出的，特别是其中的框架条件（定义6（3））。以下将证明R+的推理语义和关系语义是等价的。既然对于关系语义来说，R+是可靠的和完全的，由此可以得到R+关于推理语义也是可靠的和完全的。

R+是LR+的公理化系统。推理语义是对于推理结构的刻画，有明确的推理背景。从这个角度看，R+是关于推理的系统。

4 R+的关系语义和推理语义的等价性

定义9设M,M′是任意的两个模型。M与M′是等价的，如果对于任意公式A，A在M上有效，当且仅当，A在M′上有效。

定义10设S是任意相干逻辑系统。S的关系语义和推理语义是等价的，如果

（1）任给S的推理语义模型M，存在S的关系语义模型M，M和M是等价的；

（2）任给S的关系语义模型M，存在S的推理语义模型M，M和M是等价的。

命题1任意R+的推理语义模型也是R+的关系语义模型。

证明.设M=〈Z,R,r,⊩〉是R+的推理语义模型。按定义2，需证（1）〈Z,R,r〉是R+的关系语义框架，以及（2）⊩是关系语义模型的赋值。

（1） 〈Z,R,r〉是R+的关系语义框架。因为〈Z,R,r〉是R+的推理语义框架，按定义6，Z非空，r∈Z，即满足定义1(1)和(2)。下证〈Z,R,r〉满足定义1(3)(i)-(v)。

由定义6(3)(i)[ra]⊆a和(ii)[aa]⊆a，直接可得Rraa和Raaa。

(iii)Rabc⇒Rbac。由定义6(3)(iii)有[ba]⊆[ab]，由此可得对任意的公式集c，[ab]⊆c⇒[ba]⊆c，即Rabc⇒Rbac。

(iv)R2(ab)cd⇒R2a(bc)d，即∃x(Rabx∧Rxcd)⇒∃x(Raxd∧Rbcx)。

由定义6(3)(iv)可得[[ab]c]⊆d⇒[a[bc]]⊆d，即R[ab]cd⇒Ra[bc]d。因为[ab]⊆[ab]总是成立的，所以总有Rab[ab]。类似地，总有Rbc[bc]。于是有(Rab[ab]∧R[ab]cd)⇒(Ra[bc]d∧Rbc[bc])。由此可得

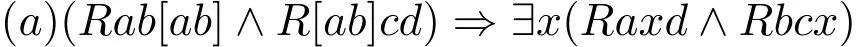
因为总有Rab[ab]，所以有∃x(Rabx∧Rxcd)⇒Rab[ab]。再由定义6(3)(i)和(v)可得∃x(Rabx∧Rxcd)⇒R[ab]cd。于是有

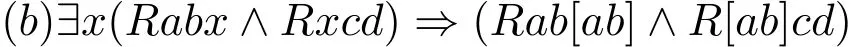
由(a)和(b)，可得∃x(Rabx∧Rxcd)⇒∃x(Raxd∧Rbcx)。

(v)Rabc且Rra′a⇒Ra′bc。由定义6(3)(v)有[ra′]⊆a⇒[a′b]⊆[ab]。

由此可得[ra′]⊆ a⇒ ([ab]⊆ c⇒ [a′b]⊆ c)。于是有[ra′]⊆ a并且[ab]⊆c⇒[a′b]⊆c。这就是Rabc且Rra′a⇒Ra′bc。

（2） ⊩是关系语义模型的赋值关系。按定义2只需证，对于任意的变元p，如果M,a⊩p，并且Rrab则M,b⊩p。设M,a⊩p，根据定义5，有p∈a。由定义6，Th(R+)⊆r，所以p→ p∈r。由p→p∈r和p∈a，可得p∈[ra]。又因为Rrab，按定义即[ra]⊆b。所以有p∈b。由此可得M,b⊩p。 □

定义11设M=〈K,R,0,⊨〉是任意的关系语义模型。s(M)=〈s(K),s(R), s(0),s(⊨)〉是M的公式化模型（formulistic model），如果

（1） 对于任意a∈K，s(a)={A|M,a⊨A}；

（2） s(K)={s(a)|a⊨K}；

（3） 对任意的a,b,c∈s(K)，s(R)abc，当且仅当，[ab]⊆c；

（4） s(⊨)是推理语义的赋值映射⊩。

s(M)中的〈s(K),s(R),s(0)〉部分称为〈K,R,0〉的公式化框架。

命题2设F=〈K,R,0〉是任意关系语义框架，s(F)=〈s(K),s(R),s(0)〉是F的公式化框架。如果F是一个R+的关系语义框架，那么s(F)是R+的推理语义框架。

证明.因为〈K,R,0〉是一个R+的关系语义框架，K∅，0∈K，所以s(K)∅，s(0)∈s(K)，s(F)满足定义6中的(1)和(2)。以下证s(F)满足定义6(3)(i)-(v)。

关于条件(i)，即证对任意的a，[s(0)a]⊆a。设a是s(K)中的任意元素。由定义11，存在a∈K,a=s(a)。M是R+模型，所以有R0aa。于是，对任意的公式A,B，如果M,0⊨A→B，且M,a⊨A，那么M,a⊨B。由此可得，如果A→B∈s(0)且A∈s(a)，则B∈s(a)。这就是[s(0)a]⊆a。

关于条件(ii)，即证对任意的a，[aa]⊆a。由定义11，不妨设存在a∈K,a=s(a)。F是R+的关系语义框架，所以有Raaa。于是，对任意的公式A,B，如果M,a⊨A→B，且M,a⊨A，那么M,a⊨B。由此可得，如果A→B∈s(a)且A∈s(a)，则B∈s(a)，即[aa]⊆a。

关于条件(iii)，即证对任意的a,b，[ba]⊆[ab]，也即对任意的c，[ab]⊆c⇒[ba]⊆c。设A,B是任意公式，A→B∈b且A∈a。因为A→((A→B)→B)是R+定理（由A4和A1可得），所以A→((A→B)→B)∈s(0)。又因为有s(R)s(0)aa,A∈a，所以(A→B)→B∈a。由(A→B)→B∈a和A→B∈b可得B∈[ab]。因为[ab]⊆c，于是B∈c。

关于条件(iv)，即证对任意的a,b,c，[a[bc]]⊆[[ab]c]，这是对任意的d，[[ab]c]⊆d⇒ [a[bc]]⊆d。此证明需要解决的是，对任意的A,B，假设有(1)A→B∈a，(2)A∈[bc]，再由(3)[[ab]c]⊆d，推出B∈d。

由(2)，可得存在公式C，(4)C→A∈b，且(5)C∈c。设E=(C→A)→((A→B)→(C→B))。因为E是R+定理，所以E∈s(0)。再由(4)和s(R)s(0)bb（以上所证条件(ii)），可得(A→B)→(C→B)∈b。再由(1)，可得C→B∈[ba]。又因为有[ba]⊆[ab]（以上所证条件(iii)），可得C→B∈[ab]。再由(5)，可得B∈[[ab]c]。于是，由(3)，B∈d。

关于条件(v)，即证对任意的a,b，[ra′]⊆a⇒[a′b]⊆[ab]。设B∈[a′b]。由此又可设，存在A，A→B∈a′且A∈b。因为A→A是公理，所以(A→B)→(A→B)∈r。又因为A→B∈a′，[ra′]⊆a，所以A→B∈a。再由A∈b，所以B∈[ab]。 □

命题3设M=〈K,R,0,⊨〉是任意关系语义模型。如果M是一个R+模型，那么M的公式化模型s(M)=〈s(K),s(R),s(0),s(⊨)〉是R+的推理语义模型。

证明.由命题2，〈s(K),s(R),s(0)〉是推理语义框架。s(⊨)即⊩，是推理语义模型中的赋值，所以s(M)是推理语义模型。 □

命题4设M=〈K,R,0,⊨〉是任意关系语义模型，s(M)=〈s(K),s(R),s(0), s(⊨)〉是M的公式化模型，A是任意的公式。对任意的a∈s(K),s(M),a⊩A，当且仅当，A∈a。

证明.对于变项，由定义5(2)(i)，命题成立。

设A∧B∈a。a∈s(K)所以存在a∈K，M,a⊨A∧B。按定义2，有M,a⊨A且M,a⊨B。于是，有A∈a且B∈a。由归纳假设，s(M),a⊩A且s(M),a⊩B。再由定义5，可得s(M),a⊩A∧B。

A∨B与A∧B类似。

设A→B∈a，对任意的b,c∈Z，如果Rabc且A∈b则B∈c。由归纳假设，对任意的b,c∈Z，如果Rabc且s(M),b⊩A则s(M),c⊩B。按定义5，即s(M),a⊩A→B。

命题5设M=〈K,R,0,⊨〉是任意关系语义的R+模型。如果s(M)=〈s(K),s(R),s(0),s(⊨)〉是M的公式化模型，那么M与s(M)等价。

证明.设A是任意公式。由命题4，可得s(M),s(0)⊩A当且仅当A∈s(0)。又因为A∈s(0)当且仅当M,0⊨A，所以有s(M),s(0)⊩A当且仅当M,0⊩A。

命题6R+的关系语义和推理语义是等价的。

证明.由命题1可得，对于R+的任意推理模型M，存在R+的关系语义模型M，M和M是等价的。由命题3和命题5可得，对于R+的任意关系模型M，存在R+的推理模型M，M和M是等价的。由定义10，命题成立。 □

5 相干逻辑的关系语义究竟刻画的是什么

自相干逻辑的关系语义产生以来，关于这个语义的直观意义是什么的问题就一直为逻辑学家们所关注，出现了多种解释。Dunn（[5]）将K解释为信息片段的集合，Rabc表示“信息状态a和b的并包含在信息状态c中”。Barwise（[3]）以及Restall（[9]）提出了途径论（Channel Theory）的解释。这一解释认为K可被视为是信息论（Information Theory）中的位置（site）和途径（channel）所构成的集合。位置是接收信息的一个情境，途径则是传递信息的渠道。在这种解释下，如果a是一个途径，b和c是位置，那么Rabc就表示途径a连接了位置b和c。Mares（[7]）和Israel&Perry（[4]）在其所构建的信息论基础上对此提出了世界及其之中信息之间关联性的解释。他们认为，每个世界都包含了某种信息之间的关联性。例如在现实世界中，根据牛顿力学，如果x和y是有质量的物体，那么它们就会相互吸引。设a表示现实世界，b表示x和y是有质量的物体这一信息，c表示x和y相互吸引这一信息，于是Rabc表示的是，在世界a中，如果b（x和y是有质量的物体）那么c（x和y相互吸引）。Mares（[8]）用情景化蕴涵（situated implication）解释相干蕴涵，关系语义模型中的K被解释为情景的集合。如果a、b是任意两个情景，P是任意命题，I是描述情景化蕴涵的三元关系，那么Iab‖P‖就表示了a和b中的信息蕴涵了这样一个情景的集合，P在该集合中的任意情景上都为真。于是，蕴涵式A→B在情景a中为真，当且仅当，对于所有使得A为真的情景b来说，Iab‖B‖成立。在此基础上，Rabc表示的是c属于任意使得Iab‖P‖成立的命题P。胡光远（[14]）再述了这一解释。

这些解释的一个共同特点就是都与信息相关，关系语义中的三元关系或者是信息之间的关系，或者是信息与世界、情境相关的关系。4这个现象大概与推理语义产生的过程有关。Dunn&Restall（[6]）指出这一语义是由Routly和Urquhart在二十世纪六十年代和七十年代所分别提出的操作语义（operational semantics）的发展。操作语义中的框架是一个三元组〈K,◦,0〉，其中K是信息片段（pieces of information）的集合，◦是K上信息片段之间的复合运算，0表示的是“空的信息片段”。按照这些解释，相干逻辑就应该是关于信息之间的关系的逻辑，但这与相干逻辑的发展历史并不相符。相干逻辑产生于上世纪六十年代，直接的动因是消除蕴涵悖论或蕴涵怪论。蕴涵悖论最早出现于实质蕴涵。所谓“悖论”，不过是直观上的推出关系与实质蕴涵的不同。为消除实质蕴涵悖论，C.I.Lewis以日常推理的推出关系为原型，提出了严格蕴涵，并构建了严格蕴涵系统。但是不久人们发现严格蕴涵也有悖论问题。为消解严格蕴涵悖论，上世纪五十年代至六十年代，在莫绍揆、W.Ackerman等人工作的基础上，A.Anderson和N.Belnap建立了以相干蕴涵为核心的相干逻辑（[13]，第8-9页）。从这个过程可以看出，相干逻辑是围绕推理问题产生和发展起来的逻辑分支，但是目前相干逻辑关系语义的各种直观解释与此并不吻合，让相干逻辑看起来是关于信息处理的逻辑，这或许是让人不满意这些解释的原因之一。5在本文的写作过程中，我们询问了N.Belanp关于关系语义的三元关系直观意义的问题。Belnap在回复中说：“我花了很多年来考虑相干逻辑中三元关系的问题。最后，关于三元关系的直观意义，我所能说的也就是Anderson&Belnap（[2]）中三处非常短的引述。这三处引述是由R.Meyer、A.Urquhart和K.Fine发现的。关系语义虽然形式上非常漂亮，但是我却不知道它到底在说什么。因为这三条引述非常短，所以我认为没什么人能在关系语义的直观意义问题上说些更多的东西。……但是在我看来，这始终是‘眼中的沙子’”。

当然，历史的原因或人们构造某种逻辑的动因与实际得到的逻辑可能会有偏差，Lewis的严格蕴涵逻辑就是一例。Lewis希望得到刻画日常推理的逻辑，但是严格蕴涵逻辑走向了关于必然性和可能性的逻辑之路，Lewis也由此成为现代模态逻辑的创始人。尽管相干逻辑是沿着Lewis所希望的方向继续前进，但是难免也出现同样的情况，实际上走向了信息处理的方向。总之，历史的原因还不能作为相干逻辑究竟是什么逻辑最具决定性的证据。这个最后的证据只能是其形式语义的直观。

推理语义有明确的推理背景，特别是其中的三元关系，一开始就明确提出，这是推理中的规则集、前提集和结论集三者之间的关系，因此推理语义的框架和模型实际上就是对于推理形式结构的刻画。本文以相干逻辑系统R+为例，证明了关于R+推理语义本身就是关系语义（命题1），而且与关系语义是等价的（命题6）。虽然这只是一个例子，但是其中已经包含了主要的要点，并且展示了具体的细节。根据这个例子，有理由认为，将关系语义做推理的解释更为合理。实际上，相干逻辑提出的基本思想就是试图通过满足相干原则的蕴涵来表达推理前提和结论之间的内容联系，以解决各种真值蕴涵的前件和后件在内容关联上的不足这个问题。在这样的思想下建立的系统，最后得到了本质上是关于推理形式结构的关系语义学，应该说也是顺理成章的结果。

从推理形式结构的角度看，不仅推理语义的解释更为直观，而且在这个大的背景下，其中的关系条件也可以得到合理的解释。例如，关于系统R+的关系语义中的几个条件关系（定义1(3)）的解释：

R0aa表达的是，逻辑规则可以用于任何前提集，推出的结论不会超出这个前提集本身；

Raaa表达的是，任何公式集都可以即做规则集又做前提集，推出是结论不会超出自己；

Rabc⇒Rbac表达的是规则集和前提集可以互换；

R2(ab)cd⇒R2a(bc)d是最为复杂的条件，从命题2关于条件(iv)的证明看，主要是用到了(C→A)→((A→B)→(C→B))，所以，这个性质所对应的其实主要就是三段论推理。

Rabc且R0a′a⇒ Ra′bc表达的是在推理语义中，R的这个性质对应于[ra′]⊆a⇒[a′b]⊆[ab]。这说明，如果a包含了逻辑规则和a′推出的结论集[ra′]，那么，用a′做规则集能推出什么，用a做规则集也能推出什么。这是推理的单调性（增加了前提还可以推出原来可以推出的结论）。

这些解释同时也表明了R+是关于什么推理的逻辑。

当然，关系语义模型和推理语义模型还是有所不相同的模型。为刻画推出关系，推理语义模型要求论域中所有的元素都是公式集，而关系语义模型中却没有这样的要求。从这点看，关系语义比推理语义更抽象，所以也有更广的应用范围。但是这并不表明这些应用都是关系语义的基本直观意义。可能世界语义学也有类似情况。从抽象的形式语义看，可能世界语义学中的框架〈W,R〉只要求W是非空集，R是W上的二元关系，可能世界语义也因此有了广泛的应用范围，如语言分析，数学结构和计算机状态及其关系的各种刻画，但是这并不妨碍我们仍然将W看做是可能世界的集合，R看做可能世界之间的可及关系。这就是可能世界语义学的直观。

相干逻辑的出现是为了刻画推出关系。从推理的直观看，关系语义提供了对于推理结构的形式刻画。这一解释为相干逻辑的关系语义提供了一个合适的直观理解，也为相干逻辑的产生和发展历程提供了合适的解释。

6 结语

对于相干逻辑来说，基于三元关系形成的关系语义在技术上可以说是一个完美的语义，但是长期以来这个语义的直观意义是什么并没有令人满意的回答。这个问题涉及到相干逻辑是什么逻辑的问题。其中的关键是这个语义中的三元关系究竟是什么关系。推理语义对此给出了一个推理要素之间关系的解释，由此构造了表达推理形式结构的推理语义框架和模型。推理语义框架和模型有明确的直观意义。从推理语义模型与关系语义模型的等价关系上看，推理语义完全可以作为关系语义向推理的直观解释过渡的一个中间环节。由此不仅使得相干逻辑的关系语义有了推理结构的解释，同时也说明了相干逻辑是一种关于推理的逻辑。这与相干逻辑产生的历史也完全吻合。

本文只是以相干逻辑R+的关系语义为例来说明我们的观点。推理语义具有一般性，这里的讨论应该也可以推广到其他相干逻辑的关系语义，甚至更为一般的关于推理的逻辑的研究。

[1] A.R.Anderson and N.Belnap,1975,Entailment:The Logic of Relevance and Necessity,volume I,Princeton:Princeton University Press.

[2] A.R.Anderson,N.Belnap and J.M.Dunn,1992,Entailment:The Logic of Relevance and Necessity,volume II,Princeton:Princeton University Press.

[3] J.Barwise,1993,“Constraint,channels and the flow of information”,in P.Aczel,D. Israel,Y.Katagiri and S.Peters(eds.),Situation Theory and Its Application,3,pp.3-27,Stanford:CSLI Publication.

[4] D.D.Israel and J.Perry,1990,“What is information?”,in P.Hanson(ed.),Information,LanguageandCognition,6,pp.1-19,Vancouver:UniversityofBritishColumbia Press.

[5] J.Dunn,1986,“Relevance logic and entailment”,in D.Gabbay and F.Guenthner (eds.),HandbookofPhilosophicalLogic,3,pp.117-124,Dordrecht:RiedelPublishing Company.

[6] J.DunnandG.Restall,2002,“Relevancelogic”,inD.GabbayandF.Guenthner(eds.), Handbook of Philosophical Logic 2nd,6,pp.86-98,Netherlands:Kluwer Academic Publishers.

[7] E.Mares,1997,“Relevant logic and the theory of information”,Synthese,109:354-360.

[8] E.Mares,2004,Relevant Logic:A Philosophical Interpretation,Cambridge:Cambridge University Press.

[9] G.Restall,1996,“Information flow and relevant logics”,in D.W.J.Seligman(ed.), Logic,Language and Computation,1,pp.463-478,Stanford:CSLI Publication.

[10] R.Routley and R.Meyer,1972,“The semantics of entailment,II”,Journal of Philosophical Logic,(1):53-73.

[11] R.Routley and R.Meyer,1972,“The semantics of entailment,III”,Journal of Philosophical Logic,(1):192-208.

[12] R.Routley and R.Meyer,1973,“The semantics of entailment”,in H.Leblanc(ed.), Truth,Syntax and Modality,pp.199-243,Amsterdam:North-Holland.

[13] 冯棉，相干逻辑研究，2010年，华东师范大学出版社。

[14] 胡光远，“相干逻辑的情境论解释”，逻辑学研究，2013年第6卷第4期，第105-115页。

[15] 周北海，“衍推系统Efde的推理模型”，自然辩证法研究（增刊），1996年，第10-12页。

[16] 周北海，“推理、推理模型和推理语义”，逻辑今探——中国逻辑学会第五次代表大会暨学术讨论会论文集（1996），1999年，中国社会科学文献出版社，第3-15页。

（责任编辑：潘琳琦）

An Explanation for the Relational Semantics of Relevance Logic

Beihai Zhou
Department of Philosophy,Peking University zhoubh@phil.pku.edu.cn
Qing Jia
Institute of Philosophy,Chinese Academy of Social Sciences v100jq@163.com

Relationalsemanticsisoneofthemostpopularsemanticsforrelevancelogic.However,because this semantics is a kind of“purely”formal semantics,the ternary relation R lacks intuition,and that is why there are various interpretations for relational semantics.As to our opinion,R is a representation of the relation among rules,premises and conclusions.Basedonthisopinion,inferencesemanticsispresented.Thebackgroundof inference semantics is the formal structure of inference and this feature makes inference semantics intuitive for our understanding.In this paper,we will prove that relational semantics and inference semantics are equivalent with respect to the relevance logical system R+.From this equivalence relation,inference semantics could be viewed as an intermediate link for the intuitive interpretation of relational semantics.By inference semantics,relational semantics could got an interpretation from the structure of inference.Relevance logic is a logic of inference,so inference semantics is coincident with the history of relevance logic.

B81

A

1674-3202(2015)-01-0050-15

2015-01-20

国家社科基金重大项目（批准号12&ZD119）。

†致 谢：感谢Nuel D.Belanp在本文写作中所给予的支持。冯棉教授阅读了初稿，指出了其中的一个错误，特此致谢。