忆阻混沌系统的同步*

陈福利(重庆师范大学数学学院，重庆401331)

忆阻混沌系统的同步*

陈福利
(重庆师范大学数学学院，重庆401331)

摘要:忆阻器之所以引起了人们的大量关注，是因为它具有其一些特殊的特点，在普通的混沌系统中代替蔡氏二极管通过用忆阻器，因之得到了一个忆阻混沌系统;研究了忆阻混沌系统的同步，通过用Lyapunov稳定性理论，并设计一个脉冲控制器来实现忆阻混沌系统在不同的条件下的同步，从理论分析上说明了结果的有效性。

关键词:忆阻器;混沌系统;同步

蔡少棠教授［1］在1971年第一次提出了”忆阻器”的观点，它被当做是电感、电阻、电容除外的又一个基本电路元件，当电荷流过忆阻器两端时，忆阻器可以记住当前的电荷量，又因为这样，所以忆阻器又被称之为“记忆电阻”。忆阻器是一个非线性的且是无源的元件，显示了许多特别的性质［2］，辅助研究人员用忆阻器解释了纳米系统中的几种现象，例如:在自旋电子元件和热敏电阻中，研究人员在HP实验室中把忆阻器用在一个大的密度存储空间里，成功的构造了一个简单的数据存储装置。忆阻器非常容易发生混沌振荡信号，于是，大量研究人员通过采用忆阻器，创建了忆阻混沌系统［3－5］。Itoh和蔡少棠［3］引进了一个拥有分段线性严格增加的弧线忆阻模型，取代了线性振荡器中的蔡氏晶体二极管，得到了一个含有忆阻器的混沌系统，并对它的动力学特性进行了分析。其后Muthuswamy选用一个分段不连续的线性忆阻器导函数，替换了蔡氏二极管，形成了一个崭新的忆阻混沌系统［3］，忆阻器从出现开始，它的使用范围［6］和应用条件［7］吸引了研究者的注意。

近年来，Strukov等人［5，8］发明了一些具有记忆特点的元件之后，忆阻器应用在混沌系统中非常广泛:可用于电路的设计或对生物的记忆特点进行实验等，文献［3，4］采用的忆阻器造成了忆阻或忆导都是间断的非线性函数，是因为忆阻器的特点是不光滑的间断段线性函数，并且只是简单地分析了所提出混沌电路的动力学特点，在此基础上，利用混沌动力学特征和以往研究过的理论分析方法，现将对其进一步研究忆阻混沌电路的同步问题。

1　模型建立

在2008年，Itoh和蔡少棠提出了一个用忆阻器代替了蔡氏二极管，导推出了一个四阶忆阻混沌电路，如图1所示。

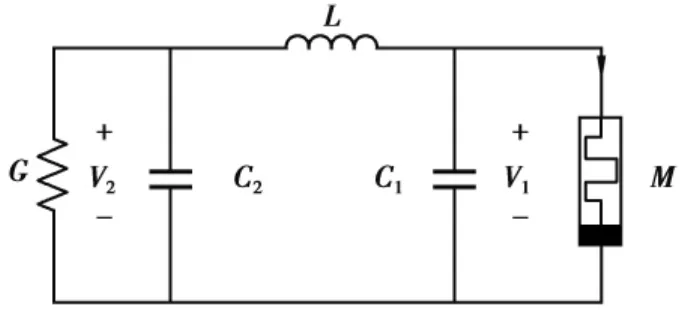
图1　四阶忆阻混沌电路

利用这个电路导出了忆阻混沌电路的方程:

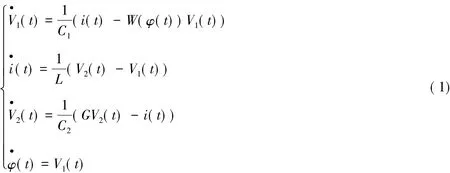
令x1(t) = V1(t)，x2(t) = i(t)，x3(t) = V2(t)，x4(t) =φ(t)，G = 1，以及定义忆导函数:W(φ) =－a+3bφ2其中(a＞0，b＞0，φ是忆阻元件的状态变量)，式(1)的状态方程可改写成无量纲的状态方程:

图1的所示的忆阻混沌电路系统是一个四维系统，它的动力学特性由式(2)描述。

2　忆阻混沌系统同步的理论分析

让系统(2)作为主系统，相应的可以做出响应系统

令ei(t) = yi(t)－xi(t) (i=1，2，3，4)为系统(2)与系统(3)同步误差.为了实现系统(2)和系统(3)的同步，定义控制器ui(t) (i=1，2，3，4)如下:

系统(2)与系统(3)的同步误差系统:

最后，给出结果。

定理1假定存在常数ki＞0(i=1，2，3，4)，使得

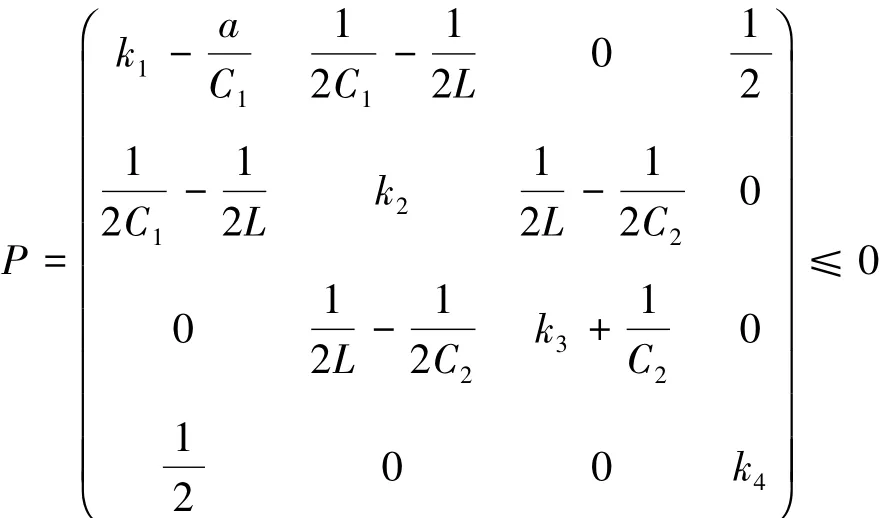
则同步误差系统(5)渐进收敛于零，并且系统(2)和系统(3)达到完全同步。

证明构造一个Lyapunov函数为

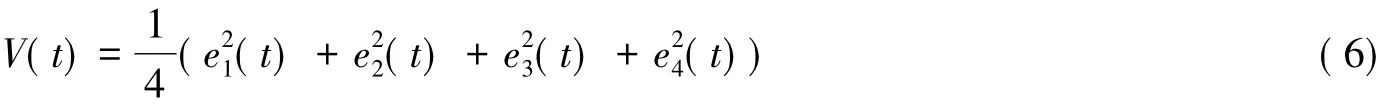
对式(6)求导:

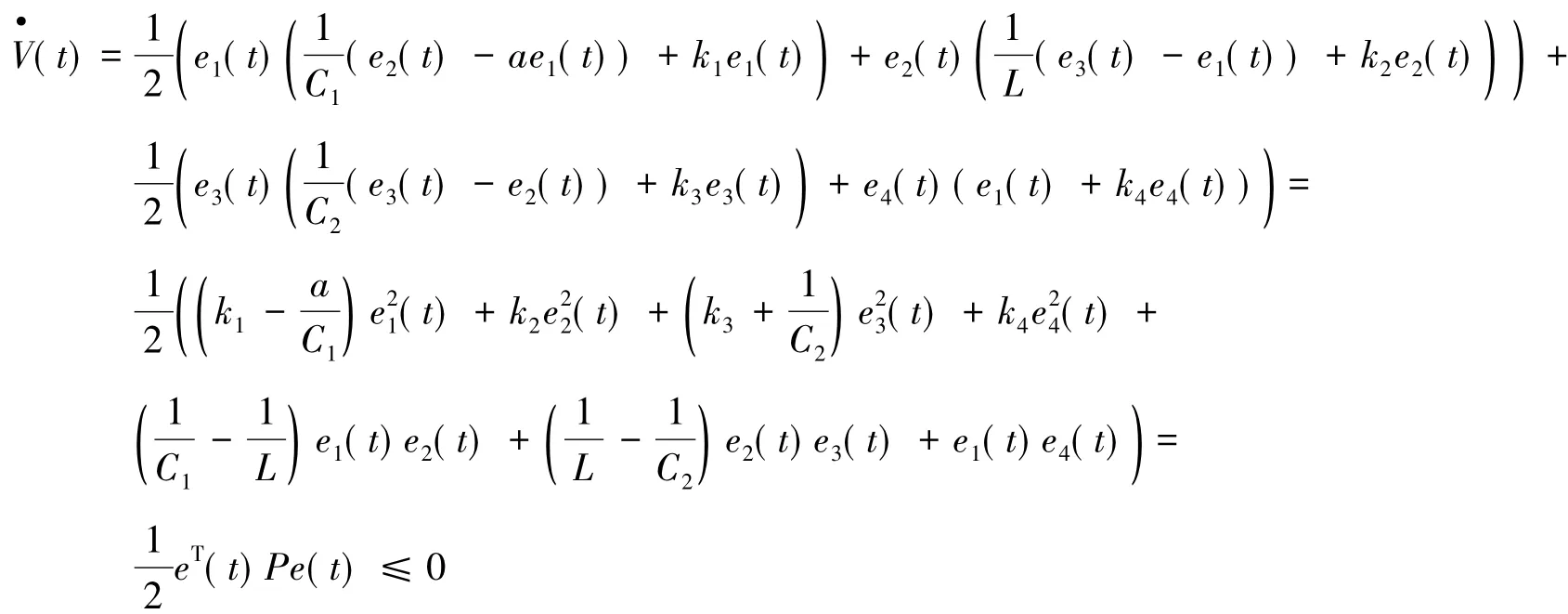
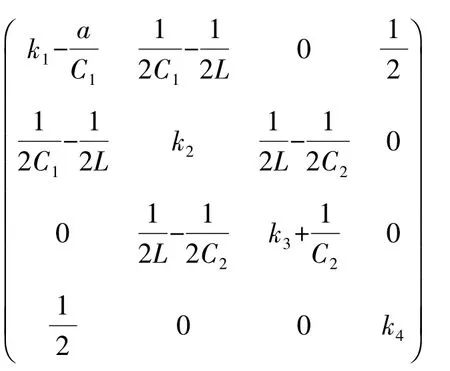
例如:选择主系统和响应系统的初始条件分别:(－0.001，0.01，0.－0.000 1)，(0，0.001，0.000 1，0)，取主

系统的参数a=1.2，C1=12，C2= 7，，控制器的参数为:k= 7.2，k=－5，k= 4.6，k= 1.5，由定理1通过1234数值模拟可知误差系统渐进趋于零，从而主系统与响应系统达到同步。

3　结束语

通过引进一个四阶忆阻混沌电路系统，在以往研究系统稳定的基础上，设计了一个控制器，使误差系统渐进收敛于零，从而主系统与响应系统达到同步。

参考文献:

［1］CHUA L.Memristor-the Missing Circuit Element［J］.IEEE Trans on Circuit Theory，1971，18(5):507-519

［2］CHUA L.KANG S.Memristive Devices and Systems［J］.Proceeding of the IEEE，1976，64(2):209-223

［3］ITOH M，CHUA L.Memristor Oscillators［J］.International Journal of Bifurcation and Chaos，2008，18(11):3183-3206

［4］MUTHUSWAMY B.Memristor Based Chaotic Circuits［J］.IETE Technical Review，2009，26(6):415-426

［5］SNIDER G，STRUKOV D，WILLIAMS R.The Missing Memristor Found［J］.Nature，2008，453:80-83

［6］SCHROEDER R.Memristor Mechanics［J］.IEEE Spectrum，2009，46(2):8

［7］CHEN G.Leon Chua’s Memristor［J］.IEEE T Circuits Syst Mag，2008，8(2):55

［8］WILLIAMS S.How We Found the Missingmemristor［J］.IEEE Spectrum，2008，45(12):24-31

Synchronization of the Memristor-based Chaotic System

CHEN Fu-li
(School of Mathematics Science，Chongqing Normal University，Chongqing 401331，China)

Abstract:Memristor draws people’s lots of attention，because it has some special features.A memristor chaotic system is obtained by substituting memristor for Chua’s Diode in normal chaotic system.This paper focuses on the synchronization of the memristor-based chaotic system.A pulse controller is designed to realize the synchronization under different conditions，and theoretical analysis proves the effectiveness.

Key words:memristor; chaotic system; synchronization

中图分类号:O157.2

文献标识码:A

文章编号:1672－058X(2015) 08－0024－04

doi:10.16055/j.issn.1672－058X.2015.0008.006

收稿日期:2014－10－28;修回日期:2014－12－04.

*基金项目:重庆市教委科研资助项目(KJ130606).

作者简介:陈福利(1990-)，女，重庆忠县人，硕士研究生，从事微分方程与动力系统研究.