时变脉冲耦合神经网络的稳定性分析*
2015-05-23彭薇重庆师范大学数学科学学院重庆404100
彭薇(重庆师范大学数学科学学院,重庆404100)
时变脉冲耦合神经网络的稳定性分析*
彭薇
(重庆师范大学数学科学学院,重庆404100)
摘要:讨论了时变脉冲耦合神经网络的稳定性问题,时变脉冲的一个重要特征是不稳定脉冲和稳定脉冲在模型中同时存在;通过控制时变脉冲强度,可以分析时变脉冲耦合神经网络的稳定性,得到满足时变脉冲耦合神经网络全局指数稳定的几个条件;最后,举例表明理论结果的有效性.
关键词:耦合神经网络;时变脉冲;指数稳定
在过去的几年里,人们讨论了许多神经网络模型,比如Cohen-Grossberg神经网络、Hopfield神经网络、和细胞神经网络[1,2].到目前为止,已经研究了许多有效的控制方法,如状态反馈控制,间歇控制,自适应控制[3-5].一般来说,有两种脉冲动力系统,脉冲序列稳定和脉冲序列不稳定.许多文献[6-11]都讨论了稳定神经网络的稳定脉冲和不稳定脉冲,大多数文献是假定不稳定脉冲和稳定脉冲单独发生,但在实践中,不稳定脉冲和稳定脉冲同时存在实际系统中.
1 预备知识
考虑耦合神经网络系统:

其中ui(t) = (ui,1,ui,2,…,ui,n)T∈Rn是状态变量,D = diag(d1,d2,…,dn)表示反馈矩阵,A = (aij)n×n,B = (bij)n×n,C=(cij)n×n是权重矩阵,f(ui(t) ) = (f1(ui,1(t) ),f2(ui,2(t) ),…,fn(ui,n(t) ) )T∈Rn是激活函数,I(t)表示在t处的外部输出的向量函数,gi:Rm→Rn是非线性耦合函数,τ(t)是时变延迟.假设耦合神经网络式(1)与没有孤立的集合连接,那么耦合函数gi(u1(t),u2(t),…,uN(t) )不可约.
若xi=ui-u*,其中u*是式(1)的平衡点,可得到:

其中

假设1存在正常数Lf,使

其中x,y∈Rn,且x≠y.
假设2存在正定矩阵Mij(i,j=1,2,…,N),使

现讨论时变脉冲耦合神经网络:

其中{ t1,t2,…}是严格递增脉冲点序列.假定x(t)在t=tk时刻是右连续,即,.因此,式(3)是一个右连续分段函数且在t=tk(k∈N+)处不连续.
注1 αk表示在处的脉冲影响强度.当脉冲强度时,绝对值增加.那么脉冲为不稳定脉冲.当脉冲强度时,绝对值减小,那么脉冲为稳定脉冲.现把不稳定脉冲和稳定脉冲都考虑进去了.假设不稳定脉冲强度的脉冲值取自于有限集{μ1,μ2,…,μN},稳定脉冲强度的脉冲值取自于有限集{ν1,ν2,…,νM},其中(i= 1,2,…,N,j= 1,2,…,M).假设tik↑是不稳定脉冲的脉冲强度μi的激活时间,tjk↓是稳定脉冲的脉冲强度νi的激活时间.
假设3inf{ tik↑-ti(k-1)↑} =ξi,max{ tjk↓-tj(k-1)↓} =ζi,其中tik↑,tjk↓∈{ t1,t2,…}.
定义1如果存在M>0,α>0,T0>0,使

那么式(3)是指数稳定.
引理1令x,y∈Rn,有xTy+xyT≤εxTx+ε-1yTy.
引理2令0<P∈Rm×m,0<r(t)<r,V:[0,r]→Rm,则
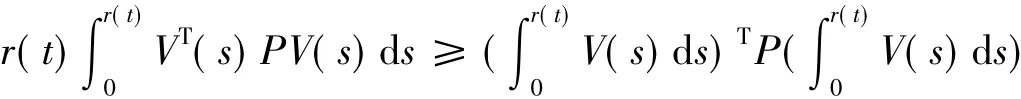
引理3假设0≤τi(t)≤τ,F(t,u1,u2,…,um):R+×R×R×…×R→R在ui处非减,Ik(u):R→R在u处非减.若

且

那么u(t)≤v(t).
2 主要结论
定理1若假设1,2,3成立,那么式(3)全球指数稳定,如果存在

其中a,b,c是正常数,使α-Rq>0成立.
证明构造李雅普诺夫函数

则有

令t=tk,由式(3),有

令ε>0,设w(t)是如下脉冲时滞系统的唯一解


由式(6),有

其中W(t,s) (t,s≥0)是下述线性系统的柯西矩阵

根据柯西矩阵的定义,有
若存在s使得在处有不稳定脉冲Ni和稳定脉冲Nj,由假设3,可以得到,那么由假设3

和式(8),有
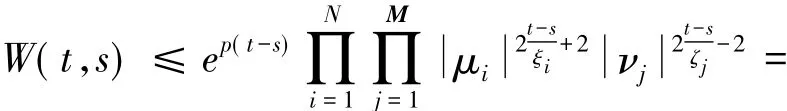


若h(w) = w-α+Rqewτ.由α-Rq>0,有h(0) =-α+Rq<0.因为h(w) = +∞且h(w)>0,存在λ>0使 h(λ) =λ-α+Rqeλτ=0.显然R-1α-q>0.那么有

相反,存在t*>0使

那么

由式(10)、(11),得到

因此式(12)成立.若ε→0,由w(t)≥V(t)≥0,有

根据定义1,式(3)是指数稳定的.
为了明显的说明不稳定脉冲和稳定脉冲的影响,假设脉冲值不变.即,μi=μ,νj=ν,ξi=ξ,ζj=ζ,tik↑=tk↑,tjk↓=tk↓(i=1,2,…,N,j=1,2,…,M).可以得到下面推论.
推论1若假设1,2,3成立,那么式(3)全球指数稳定,如果存在
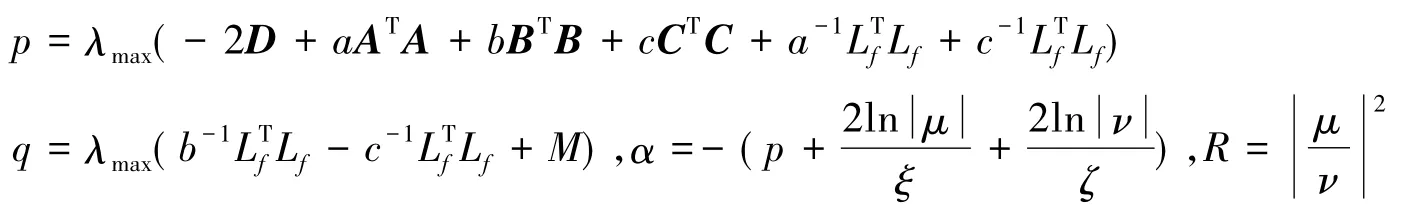
其中是正常数,使成立.
证明类似于定理1,因此省略.
3 举例
若

通过简单的计算,得到p=-1.839 4,q=1.假设μ=-1.2,ν=-0.9,ξ=0.5.根据推论1得,如果稳定脉冲序列ζ≤0.315 6那么式(3)稳定.
4 结论
在实际模型中,往往不稳定脉冲和稳定脉冲同时存在,而在许多文献中都隐性的假设了不稳定脉冲和稳定脉冲单独发生.研究了时变脉冲耦合神经网络的稳定性问题,通过控制时变脉冲强度,得到满足稳定的条件,运用例子说明了定理结果.
参考文献:
[1]GUPTA M M,JIN L,HOMMA N.Static and Dynamic Neural Networks[M].New York,Wiley-Interscience,NY,2003
[2]CAO J D,LI L L.Cluster Synchronization in an Array of Hybrid Coupled Neural Networks with Delay[J].Neural Networks,2009,22(4):335-342
[3]WU H,GUO Q.Exponential Stability of a Genetic Network Under Mixed Impulsive Control[J].Journal of Computational Information Systems,2012 (8):9561-9567
[4]YANG X,CAO J.Stochastic Synchronization of Coupled Neural Networks with Intermittent Control[J].Phys Lett A,2009(373):3259-3272
[5]WU H Q,GUO X Q,DING S B.Exponential Synchronization for Switched Coupled Neural Networks via Intermittent Control[J].Journal of Computational Information Systems,2013(9):3503-3510
[6]LI J,HO D,CAO J.A Unified Synchronization Criterion for Impulsive Dynamical Networks[J].Automatica,2010(46):1215-1221
[7]ZHANG H,GUAN Z,HO D.On Synchronization of Hybrid Switching and Impulsive Networks[J].2006 45thIEEE Conference on Decision and Control IEEE,2006:2765-2770
[8]ZHANG W B,TANG Y,FANG J A.Stability of Delayed Neural Networks with Time-varying Impulses[J].Neural Networks,2012 (36):56-63
[9]QI J T,LI C D,HUANG T W.Stability of Delayed Memristive Neural Networks with Time-varying Impulses[J].Cogn Neurodyn,2014(8):429-436
[10]SONG Q K,ZHAO Z J.Cluster Local and Complete Synchronization in Coupled Neural Networks with Mixed Delays and Nonlinear Coupling[J].Neural Comput Appl,2014(24):1101-1113
[11]WANG G,SHEN Y.Exponential Synchronization of Coupled Memristive Neural Networks with Time Delays[J].Neural Comput Appl,2014(24):1421-1430
The Stability Analysis of Time-variant Impulse Coupled Neural Networks
PENG Wei
(School of Mathematics Science,Chongqing Normal University,Chongqing 404100,China)
Abstract:This paper dissusses the stability of time-variant impulse coupled neural networks.The main feature of time-variant impulse is the coexistance of unstable impulse and stable impulse in model.The stability of timevariant impulse coupled neural networks can be analyzed by controlling the intense of time-variant impulse.Several conditions for globle exponential stability of time-variant impulse coupled neural networks are obtained.Finally,an example is given to prove the effectiveness of the theory.
Key words:coupled neural networks; time-variant impulse; exponential stability
中图分类号:O231
文献标识码:A
文章编号:1672-058X(2015) 08-0009-05
收稿日期:2014-10-07;修回日期:2014-12-15.
*基金项目:重庆市教委科研资助项目(KJ130606).
作者简介:彭薇(1990-),女,湖北恩施人,硕士研究生,从事脉冲控制研究.
doi:10.16055/j.issn.1672-058X.2015.0008.003
