铅球运行的再认识——基于动力学方程<br/>

铅球运行的再认识——基于动力学方程

2015-05-23张伟

体育科学研究 2015年6期

张伟

(北京体育大学研究生院，北京100084)

以中国知网期刊为检索数据源，检索主题为力学，并含铅球，精确匹配2004-2014年发表于核心期刊的论文，见附录1。从中可以发现，有20篇论文主要是通过生物力学的方法进行了研究，对铅球出手前的各项身体参数进行了详细地分析，大致有两个目的:使读者了解优秀运动员的生物力学特证;探求出手角度和初速度的最佳组合方式;有2篇论文是运用了质点动力学和数学相结合的方法，但解释的是出手角度和初速度的关系，不是针对铅球出手后的受力进行分析。因此，本文从一个新的视角—动力学的角度分析铅球的运行轨迹，从理论的角度全面论述其受力过程。

1 研究对象与方法

本文以铅球出手到落地的整个运行过程为研究对象，并将运行过程分为两个阶段，从出手到最高点为第一阶段，铅球位于最高点时其垂直方向的速度为零;第二阶段为从最高点到落地。本文主要运用动力学定律、质点的运动微分方程和数学方程对铅球的整个运行过程进行分析，其公式的基本表达形式为:d/dt(mV)=F。运用质点运动学的方法，根据实际比赛中测得的数据，代入质点运动的微分方程，求得两种不同受力情况下铅球的水平位移，并运用SPSS进行相关性和差异性检验，为最后得出结论提供依据。本文主要分析的问题:

1)考虑铅球所有受力和只受重力两种不同的情况下，从出手到落地的运行轨迹方程;

2)根据实际比赛中测得的出手初速度和角度分析空气阻力和浮力对掷铅球的影响。

2 结果与分析

2.1 全面受力分析下的铅球运行轨迹

在牛顿的经典力学体系中，物体的质量是恒量，时间与空间也是不变的。然而人们通过对近代物理的学习已经认识到，任何物体的质量、时间和空间都是随着物体速度的变化而变动的，但当物体运行的速度远小于光速时，物体速度的变化对其质量、时间和空间的影响是可以忽略不计的(见图1、图2、图3、表1、表2、表3)。由于铅球运行时其速度(Vt≪V光速)远远小于光速，物理表达式因此本文不考虑铅球速度变化对其产生的影响。

图1 铅球在空中的运动轨迹

当一个质点受到几个力(F1，F2，…，Fn)的共同作用时，根据质点动力学第二定律，可以得出ma，矢量形式的微分方程是［2］。把整个空间看做一个三维整体，铅球在xoy平面内运行，因此可以得出铅球所受力在x轴上的投影为，在 y轴上的投影为根据图2便可得出，x轴方向md2x/dt2=f2，y轴方向 md2y/dt2=f1+G-F(上升阶段)，md2y/dt2=G-f1-F(下降阶段)。f2=fsina，取f=-μV，即阻力与速度方向相反，μ为粘滞阻尼系数。左图为上升阶段的受力情况，右图为下降阶段的受力情况。

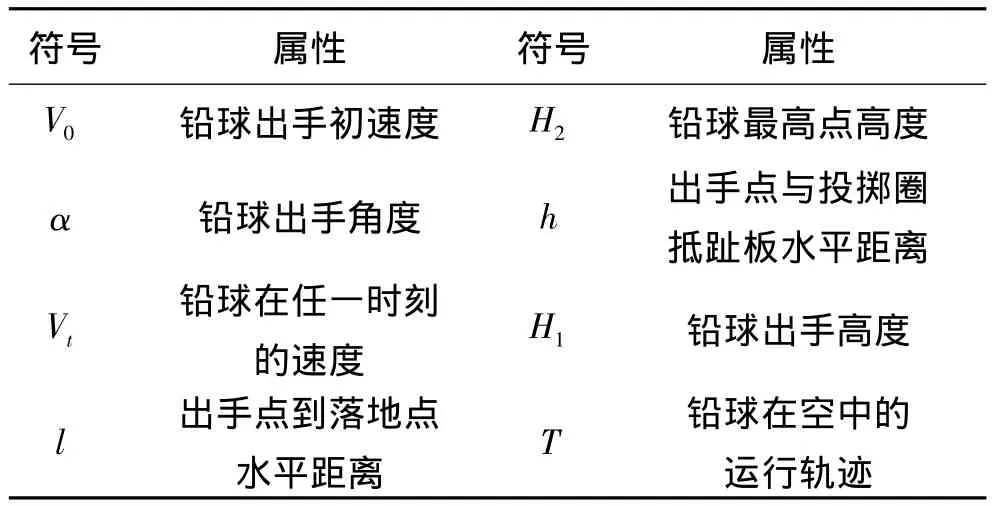
表1 图1中各符号属性

图2 铅球运行过程中的受力

表2 图2中各符号属性

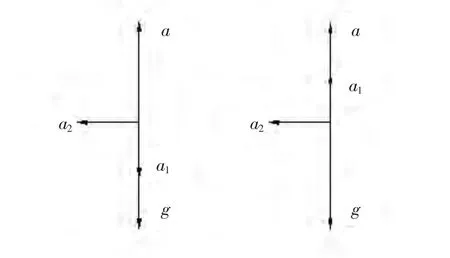
图3 铅球运行过程中的加速度

水平方向，a2=f2/m;垂直方向a1=f1/m，a=ρVg/m，V表示铅球体积，左图为上升段，右图为下降段。以出手位置为原点，y轴向下为正，如图1所示。上升阶段，铅球的运动微分方程为:，当t=0时，，对上述两式定积分可得:

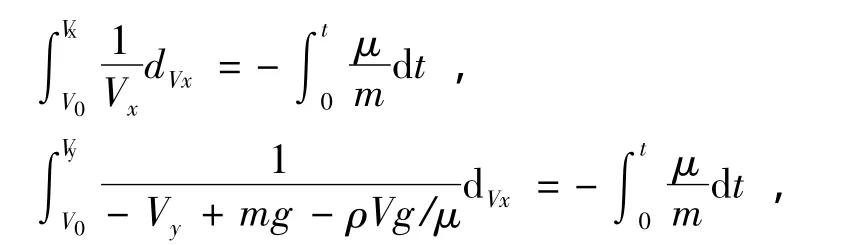
求得铅球速度随时间变化的规律为:

t=0时，x=0，y=0，在x、y轴方向上做铅球速度随时间变化的定积分得:

求得铅球在x、y轴方向的运行轨迹分别为:

即铅球在xoy平面内上升阶段的运行轨迹。下降阶段，铅球在x轴方向上的受力没有变化，因此铅球在x轴的运行轨迹不变，在y轴方向，阻力垂直分量f1方向虽然发生改变，但是始终与速度方向相反，因此铅球在y轴的微分方程同样为:

t'=0时，V'y=0，在y轴方向做铅球速度随时间变化的定积分得:

2.2 重力作用下的铅球运行轨迹

根据2.1的计算过程，将铅球的运行过程分为上升和下降两个阶段，分别建立两个不同坐标，仅考虑重力的影响，水平方向不受力的影响，垂直方向受重力影响(见图4)。上升阶段铅球速度随时间变化的规律为:

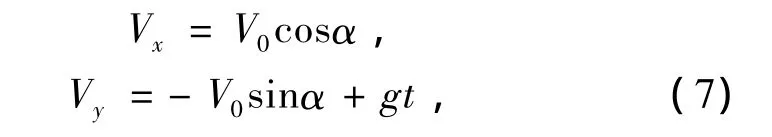
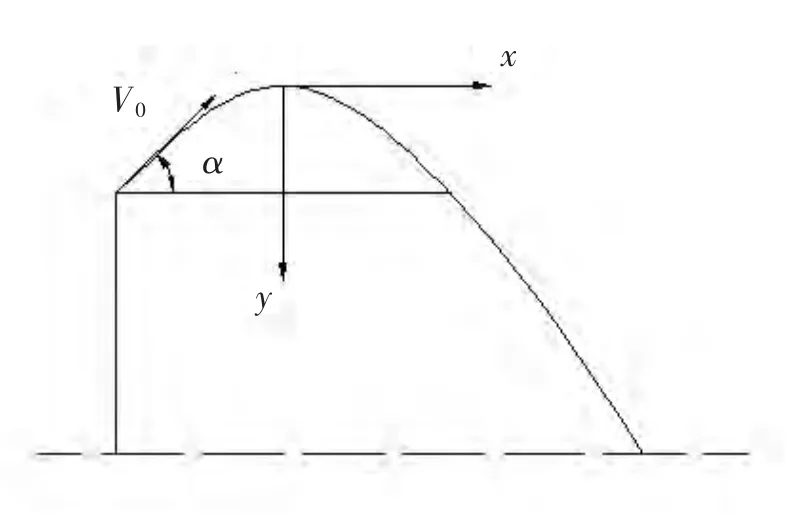
图4 铅球下降方程坐标示意图

可求得铅球的轨迹方程为:

下降阶段铅球速度随时间变化的规律为:

可求得铅球的轨迹方程为:

2.3 铅球运行轨迹分析

由铅球在x轴方向的轨迹方程可发现，铅球的投掷距离与铅球出手的初速度(V0)和出手角度α的大小呈正相关，并随着时间t的变化而改变。

当铅球位于最高点时，取垂直方向的速度为零。下面以第11届全运会女子铅球前八名为例来分析空气阻力与浮力对投掷距离的影响。

2.3.1 全面受力分析

考虑所有受力的情况下，当上升阶段Vy=0时，根据(2)式可求出铅球到达最高点的时间T，将时间T分别代入(3)(4)中，可以算出上升阶段水平方向和垂直方向的位移，如表6所示。根据H2=H1+y，将H2代入(6)中，可求得下降阶段的时间T'，将T'代入(3)中，可求得下降阶段的水平位移，从而求得总位移S1，见表5。

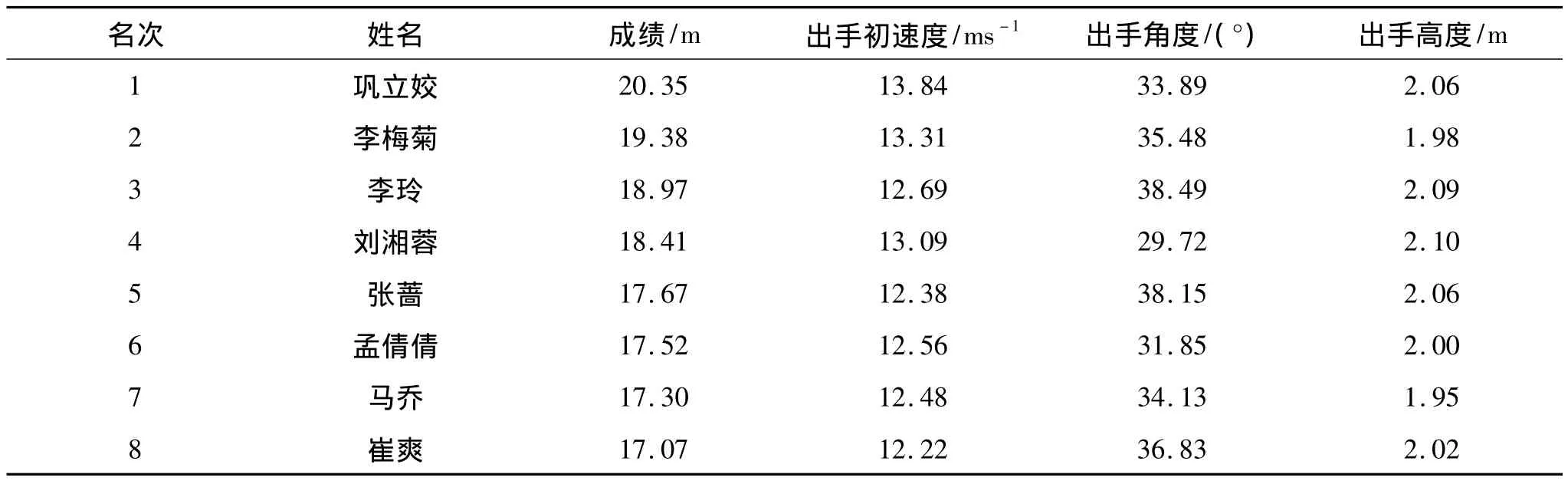
表4 第11届全运会女子铅球前八名的出手速度与角度［1］

表5 上升阶段数据

由表4可以看出，运动员的出手角度都低于45°，因此铅球出手后的速度Vx＞Vy，垂直方向的加速度远大于水平加速度，这使得铅球水平方向的位移大于垂直方向，如表5和表7所示。不论是全面受力分析下还是重力分析下，无论是上升阶段还是下降阶段，从巩立姣到崔爽，水平位移都呈现出减小的趋势，这与实际的投掷距离相符，个别数据波动比较大，这是由于实际测得的初速度和出手角度以及计算过程都存在着一定的误差。

2.3.2 重力计算

考虑只受重力的情况下，当上升阶段Vy=0时，根据⑺式可求出铅球到达最高点的时间T，见表8。将数据T分别代入(8)(9)中，可以算出上升阶段水平方向和垂直方向的移动距离，如表8所示。根据H2=H1+y，将H2代入(13)中，可求得下降阶段的时间T'，将T'代入(12)中，可求得下降阶段的水平位移，从而计算得总位移S2，计算得各项数据如表7和表8所示。

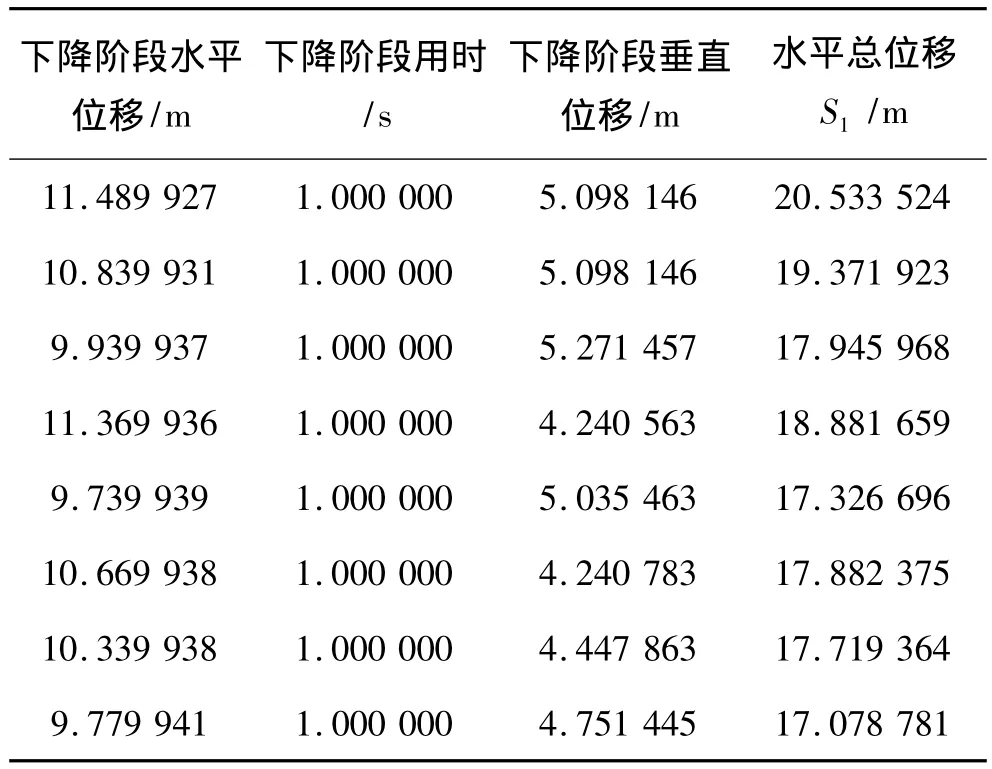
表6 下降阶段数据

表7 上升阶段数据

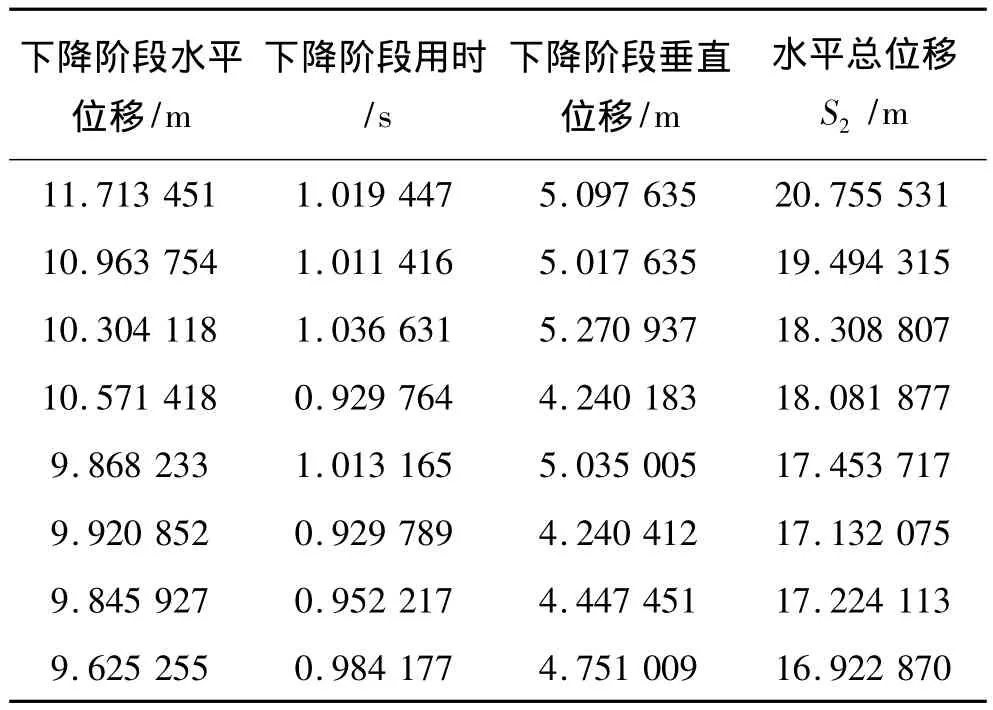
表8 下降阶段数据

根据2.3.1与2.3.2计算的结果，可求出全面受力分析与重力分析下差的绝对值，以及绝对值与实际投掷距离的比值，见表9。

由表10可以看出，水平位移差绝对值 Δ S在(0.12～0.80)m的范围内，水平位移差绝对值与实际投掷距离的比值，不同运动员的有差异，这与运动员的出手初速度和出手角度有关。如果仅求水平位移的差值ΔS，便会发现差值ΔS的方向不同，这是由于在全面受力作用下，不同运动员出手初速度和出手角度的组合不同，以及受到阻力和浮力的影响，使得求得的总时间与重力作用的总时间差值正负不同，从而使得不同运动员的ΔS方向各异。因此，不同运动员掷铅球时，空气阻力和浮力可能产生正影响，也可能产生负影响(见表10、表11)。