基于多波束测深数据滤波方法研究

闻 亚，曾 媛，芮 晔，沈 露

（1.河海大学文天学院，安徽 马鞍山 243000；2.马鞍山港口（集团）有限公司，安徽 马鞍山 243000）

1 引言

随着人口数量和工业科技的飞速发展，石油、天然气等自然资源被大量开采，陆地上的资源越来越少，海洋研究受到了前所未有的广泛重视.多波束测深系统对海底地形进行了面式全覆盖测量，所采集的数据量巨大，给后期处理带来了较大的困难.因此，有必要对多波束测深数据滤波相关方法展开深入的分析和研究.

为了解决传统人工滤波方法的效率问题，国内外研究人员提出了很多智能式的深度滤波方法，如2001年，提出了一种基于动态贝叶斯模型BDLM（Bayesian Dynamic LinearMode）的滤波方法，1998年，朱庆、李德仁将趋势面滤波的思想运用到测深异常值判定的数据处理过程中，该方法对一定范围内测深点的坐标值和水深值进行多项式趋势面拟合，通过2σ 或σ 准则进行异常值的判定；2004年，阳凡林将小波分析的思想融合至中值滤波过程以进行异常值的探测，并取得了较好的应用效果.

在总结归纳了传统的多波束测深异常值检测方法基础上，本文并结合实例数据，针对传统方法存在的不足，将改进 算法引入到测深异常值的判定中.最后对全文进行总结和提出有待进一步研究的问题.

2 基于改进GA 算法的测深异常值探测

2.1 改进GA算法的主要思想

2.1.1 初始群体的产生

对初始群体产生前对测区划分为多个子空间，以保证各个空间的水深数据是连续变化的.本文提出一种针对不规则测区的两步分区法，（如图1.1）具体步骤如下：

a，确定测区所有测深点纵向坐标y的最大值max(y)和最小值min(y)，取适当距离等分成n块，如图1.2所示.各块的横向间距Dy为：

b，记录每个横向分块内各自的最大值和最小值，并根据测深点数进行等距分块（图1.3）.设第i个横向分块内最值分别为max(x)和而min(x)，其等分间距Dxi为：

上式中，m为第j个横向分块中存在的水深点数；k为设置的每个子分区中应该包含的平均水深点数；IHI为取整运算.

图1 两步分区法示意图

2.1.2 选择算子的改进

首先要确定选择的规则，采用一种基于染色体适应度大小排序的选择算子.

2.1.3 采用自适应的交叉变异率

学者Srinvivas等人提出采用自适应遗传算法(Adaptive GA,AGA).当种群因染色体的适应度区域一致而导致局部最优却不是全局最优时，使Pc和Pm增大；当种群中染色体适应度分布比较分散时，自动减小Pc和Pm.于此同时，将较小的Pc和Pm分配给适应度高于种群中平均值的染色体，保护其进入下一代；将较大的Pc和Pm分配给适应度低于平均值的染色体，增加其被淘汰的概率.如图2所示，自适应遗传算法可以根据种群的进化程度自动调节交叉和变异率的大小，既保证了进化群体的多样性，同时也保证了算法的收敛性.

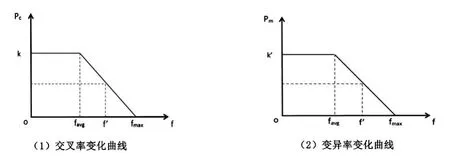
图2 自适应交叉率和变异率

在计算过程中，自适应的Pc和Pm根据下式确定：

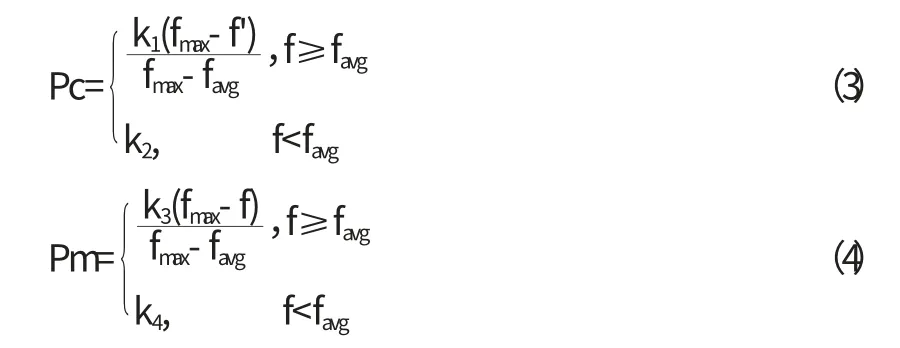
式中，fmax为种群中最大的适应度值，favg为每代群体的平均适应度值，f'为要交叉的两个个体中较大的适应度值；f为要变异个体的适应度值，k1，k2，k3，k4的取值范围为(0,1).

为了避免种群在进化初期快速收敛于局部最优解而不是全局最优解的情况出现，可将种群中最大适应度的染色体的对应的Pc和Pm调整至不等于0：

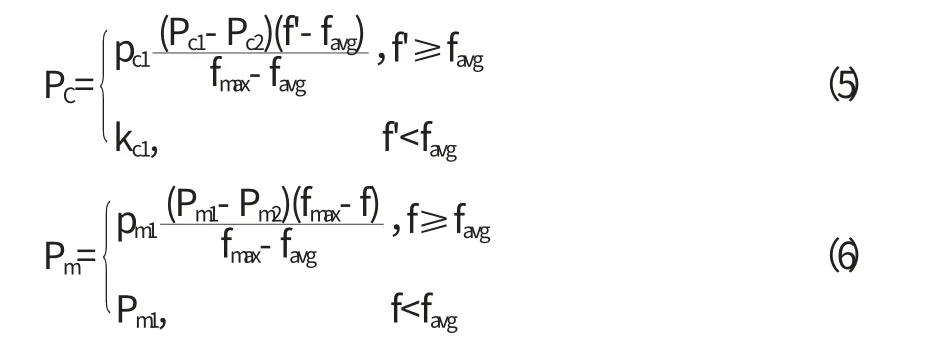
2.2 基于改进GA算法的多波束异常值探测步骤

2.2.1 初始群体编码

采用两步分区法对测区进行细分，对子空间内的水深观测值进行编码，以产生初始群体，正常水深的基因值为0，异常水深的基因值为1，在产生初始群体过程中，每个个体之间需要保持适当的海明距离.

2.2.2 适应度值标定

根据多波束水深测量值的特点，定义如下适应度函数：

式中：Zi为当前个体中基因值为0的水深值，Z为剔除异常值以外所有点水深值的平均值，N为基因值为0的样点个数.

2.2.3 运用改进的选择算子进行选择操作

计算每个初始个体的适应度值，采用基于个体适应度大小排序的选择算子对当前种群进行选择操作：适应度较高的个体复制两份，中间的复制一份，适应度较低的个体不复制.

2.2.4 采用自适应交叉变异率进行交叉和变异操作

根据式（5）和式（6）确定调整后的交叉和变异率.交叉采用两点交叉法，即在需要两两配对的母体上取两个交叉点，然后交换两个母体交叉点之间的局部染色体.根据调整后的变异率，确定需要进行变异的染色体和对应的变异点，需要进行变异操作时，对变异点上的基因值做取反运算，将0变为1或者将1变为0，从而生成新的染色体.

2.2.5 确定水深异常值

返回步骤（2），按式（7）重新计算每个新个体的适应度，并反复对种群进行遗传进化，直至种群中最高适应度值与最低适应度值小于某一限差.此时，可以认为，种群的进化趋于稳定，基本完成了多波束测深异常值的识别工作，并将当前种群中适应度最高的个体作为最优解输出.

2.2.6 拟合异常水深点的推估值

对异常值进行标定后，对于基因值为0的水深点上保留原始观测值，而对于异常值，采用区域内临近点水深值的加权平均值作为推估值.

3 实例分析

为检测改进GA算法用于多波束测深异常值探测方法的应用效果，实验采用三处由Seabat8125多波束系统采集的250m×250m实测海区水深数据进行仿真处理，三种典型海底地形形态分别为平坦地形、斜坡地形与起伏地形，其地形复杂度依次提高.如图3所示，分别在这三个海区水深数据中随机性的加入幅度大小为2σ～5σ 的小异常值，10σ～20σ 大异常值，和一部分3σ～20σ 的群簇异常值，每种异常值的数量占所有水深点数量的0.5%.图中小异常值的位置用黄色点标出，大异常值用红色点标出，而群簇异常值的位置由绿色点标出.

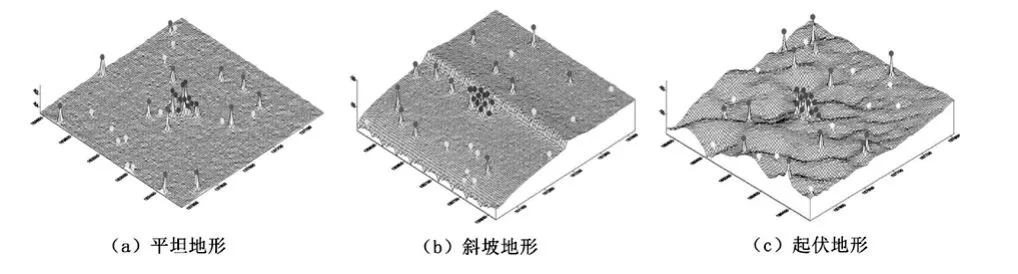
图3 加入不同幅度异常值的三种地形

分别采用5×5窗口、7×7窗口、9×9窗口大小的滑动窗口对上述三组数据进行基于改进遗传算法的异常值检测与剔除处理.表1给出了不同窗口在不同地形下滤波的平均结果，初始染色体的规模为100，交叉和变异参数取PC1=0.9，PC2=0.6，Pm1=0.1，Pm2=0.001迭代终止的条件设定值为ε=1×10-4.其中表1所列的基因值对应于地形3，7×7窗口中第23个细分区域(包含群簇异常值)的水深观测值，对比原始数据可发现，该区域仅出现1处出错情况，测深异常值基本被基因值1标定，检测效果比较好.

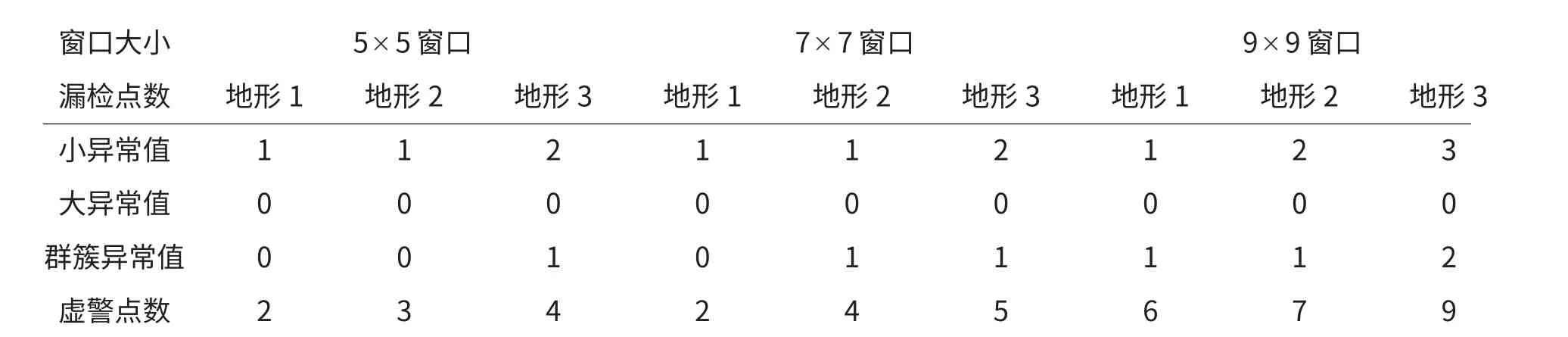
表1 不同尺寸窗口对三种地形数据进行异常值检测的出错情况统计

图4 基于改进GA算法异常值剔除效果图（窗口为7×7）

表2 第23个子区的基因值

综合以上数据，可以得出以下结论：

（1）通过图3与图4对比可发现，改进遗传算法对大异常值、小异常值、群簇异常值的检测效果都比较好，可以识别出大部分幅度不同的异常值.通过表2.4可以看出，改进GA算法直接将异常值标定为1，结果清晰明了.

（2）对比表2中数据，可发现，随着窗口大小和地形的复杂程度的变化，改进遗传算法对异常值的检测效果并未发生明显的变化，可见改进遗传算法具有较强的适应性.

（3）基于改进遗传算法检测异常值的虚警率比基于M估计的虚警率低，且虚警率随窗口尺寸的增大而增大.

4 结束语

改进GA算法直接以分区内的水深值为研究对象，并采用了改进的选择算子和自适应的交叉和变异率，大大提高了算法的稳定性，只需要给定合适的适应度函数，即可对测深异常值进行自动化式的标定，无需任何其他粗差的判定准则，具有很高的检测效率.

〔1〕刘经南,赵建虎.多波束测深系统的现状和发展趋势[J].海洋测绘,2002,22(5):3-6.

〔2〕赵建虎,刘经南.多波束测深及图像数据处理[M].武汉大学出版社,2008.

〔3〕Guenther G C,Green J E.Improved depth selection in the bathymetric swath survey system (BS3) combined offline processing (COP) algorithm[J].National Oceanic and Atmospheric Administration, Dept.of Commerce,Rockville,MD,Tech.Rep.OTES-10,1982.

〔4〕Ware C,Knight W,Wells D.Memory intensive statistical algorithms for multibeam bathymetric data[J].Computers&Geosciences,1991,17(7):985-993.

〔5〕Calder B.Automatic statistical processing of multi-beam echo-sounder data [J].International Hydrographic Review,2003,4(1):53-68.

〔6〕Jeong B, Lee Y H.Design of weighted order statistic filter using the perception algorithm.IEEE Transactions on Signal Processing,1994,42(11):3264-3269.

〔7〕Calder B R,Mayer L A.Automatic processing of high‐rate, high‐density multibeam echosounder data[J].Geochemistry,Geophysics,Geosystems,2003,4(6).

〔8〕朱庆,李德仁.多波束测深数据的误差分析与处理[J].武汉测绘科技大学学报,1998,23(1):1-4.

〔9〕张京钊,江涛.改进的自适应遗传算法[J].计算机工程与应用,2010,46(11):53-55.