基于贝叶斯压缩感知的频率步进探地雷达成像算法
2015-05-18孙延鹏王艺霖屈乐乐
孙延鹏,王艺霖,屈乐乐
(沈阳航空航天大学 电子信息工程学院,沈阳 110136)
基于贝叶斯压缩感知的频率步进探地雷达成像算法
孙延鹏,王艺霖,屈乐乐
(沈阳航空航天大学 电子信息工程学院,沈阳 110136)
针对传统压缩感知频率步进探地雷达成像算法存在计算量大和对噪声和重建正则化参数敏感的问题,提出一种基于稀疏贝叶斯学习的贝叶斯压缩感知成像算法。该成像算法的核心通过稀疏贝叶斯线性回归模型中相关向量机的学习来实现对探测场景反射系数的重构。仿真结果表明,相比其他的经典算法,所提成像算法能够更好地利用了探测场景的统计先验信息,能够更好地兼顾重构精度和计算效率。
频率步进探地雷达;贝叶斯压缩感知;成像算法
频率步进体制是探地雷达技术的工作体制之一。频率步进探地雷达是通过发射工作频率按固定间隔逐步上升的连续波,并对不同频率点回波幅度与相位信息进行数据采集的连续波雷达。随着探地雷达技术应用的进一步推进,探地雷达不断朝着多通道、多波段和高分辨率等方向发展[1],这就使得探地雷达系统的数据采集量大大增加,成像复杂度大大提高。随着压缩感知(Compressed sensing,即CS)理论[2]的提出,这一问题正得到解决,该理论证明[3]:当信号在某个变换域是稀疏或可压缩的,稀疏信号采样速率不再取决于信号的带宽,而主要取决于两个基本准则[4]:稀疏性和非相干性,突破了Nyquist理论对信号采样的限制。
目前CS 理论依旧在不断地发展,其重建算法主要包括两类[5]:一类是以基追踪算法BP(basis pursuit)[6]为代表l1的范数线性优化算法,该算法是在所有测量向量的不同组合中寻求最优化的解,因此计算复杂性较高;另一类是以正交匹配追踪算法OMP(Orthogonal Matching Pursuit)[7]为代表的贪婪算法,该算法是通过递归的方法,对已选择的原子集合进行正交化从而保证了迭代的最优性。
传统的压缩感知频率步进探地雷达存在数据计算量大和对噪声敏感的问题。针对这一问题,本文提出一种基于稀疏贝叶斯学习的贝叶斯压缩感知(Bayesian compressed sensing,BCS)频率步进探地雷达成像算法[8-9]。该算法基于贝叶斯统计学的理论[10],依据先验知识对系数向量的每一个元素赋予一个先验概率分布用以限制模型的复杂度,并引入超参数;通过最大化超参数的边缘对数似然函数,获得每个系数向量对应的先验概率分布的参数值。与传统CS成像重建算法相比,基于BCS的频率步进探地雷达成像重建算法能够较好地兼顾计算效率和重构精度,因此具有较好的成像重建性能。
1 信号模型
频率步进探地雷达成像模型[11]如图1所示,假定发射天线、接收天线与成像区域位于同一平面内。成像区域沿水平方向(x轴)和距离方向(z轴)划分为K×L个均匀的网格,每一个网格对应一个像素点。
假设测量过程中共有M个天线测量位置,发射天线在一个扫描周期中,频率从f0到fN-l共N个扫描频点,探测区域总共有P个实际散射目标数,则在第m=1,…,M个位置对复基带信号进行采样后得到复信号如下:
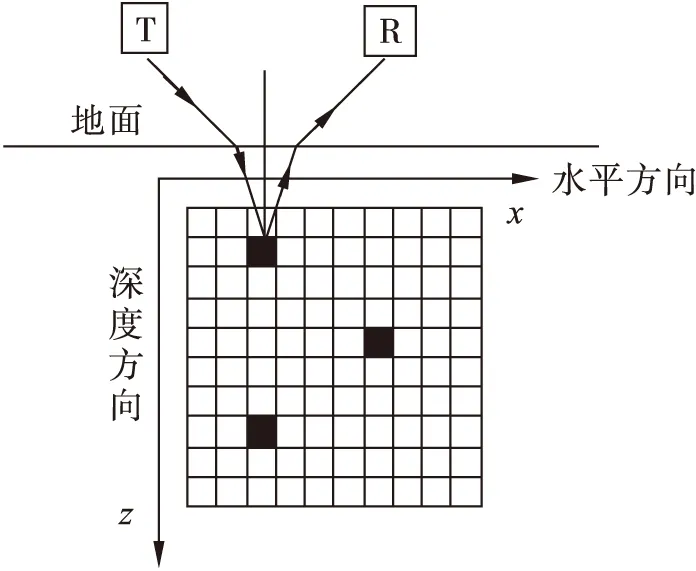
图1 频率步进探地雷达成像模型
(1)
ρp表示第p个点目标的复反射系数,τp,m表示为电磁波在第m个天线测量位置与第p个点目标的双程传输延时。
为了能够用压缩感知的模型求解出地下待成像区域的2维反射率分布r(K,L),将r(K,L)通过列堆叠转换成一个KL×1维的向量,记为wx,如图2所示。
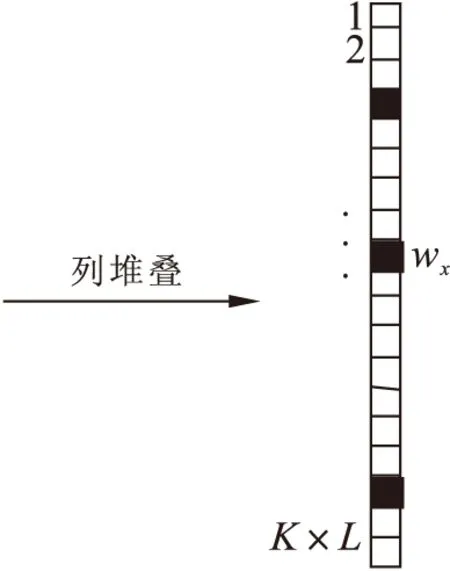
图2 网格划分示意图
系统在第m个探测位置接收到的回波信号可以表示为一个基矩阵Bm和反射系数向量wx相乘的形式,如下:
Sm=Bmwx
(2)
Sm=[s0(f0),…,sm(fN-1)]T为N×1维频域测量数据向量,[·]T表示转置,sm(fn)为当工作频率为fn时,天线在第m个测量位置采集到的回波数据。基矩阵Bm是大小为N×KL的基矩阵,其第j列为:
[Bm]j=[e-j2πf0τm,j,…,e-j2πfN-1τm,j]T
(3)

Sx=Bxwx
(4)
一般来说,反射系数向量wx是稀疏的,满足CS理论对信号的要求。为了更好地满足约束等容性条件RIP(Restricted Isometric Property)[18],我们从M个天线测量位置随机选择Q1个位置,再从选中的测量位置随机选取Q2个数据,这样构成了一个Q1Q2×NM大小的测量矩阵Ψ,并且Q1Q2≪NM,用测量矩阵Ψ对Sx进行投影可以得到:
tx=ΨSx=ΨBxwx=Φxwx
(5)
式中,Φx=ΨBx是一个大小为Q1Q2×KL的投影矩阵。
2 贝叶斯的压缩感知(BCS)
由于模型中投影矩阵的元素与回波数据均为复数,无法直接对其使用BCS算法。所以根据复数的运算法则,对式(5)中的矩阵和向量做如下变化:
(6)
(7)
其中Re(·)与Im(·)分别代表复数的实部和虚部。考虑到测量噪声,由式(5)(6)(7)可以得到:
t=Φw+n
(8)
其中测量噪声n的元素可以近似为均值是0,方差是σ2的正态分布。因此可以写出t的高斯似然函数[12]:
(9)
‖·‖表示l2范数。这样就将w的求解转换为w是稀疏的这一先验条件下的线性回归问题。通过赋予参数w={ωi}i=1,2KL一个先验分布,可以避免过拟合情况的发生。设参数ωi的先验分布是均值为零,逆方差为∂i的正态分布,所以p(w/a)的密度函数为:
(10)
其中a=[∂1,∂2,…,∂2KL]T,根据先验分布与后验分布的共轭关系,可以得到w的后验分布的形式为多元正态分布,它的均值向量μ和协方差矩阵∑如公式(11)、(12)(设∂0=σ-2):
μ=∂0∑ΦTt
(11)
∑=(∂0ΦTΦ+A)-1
(12)
其中A=diag(a),其中diag(·)表示以其中的向量作为对角元素的对角矩阵。通过观察可以发现对均值向量μ和协方差矩阵∑的求解也就是对超参数∂0和a的求解,在相关向量机[13]框架下,通过第二型最大似然估计方法(ML)[14]或者最大期望算法(EM)可以求出超参数的极值。本文采用ML的方法得到:
(13)
(14)

3 快速贝叶斯压缩感知算法
针对BCS算法计算复杂度大的问题,文献[14]提出了一种快速BCS算法,该算法对w进行边缘化处理,得到关于超参数的边缘似然函数:
L(a,σ2)=logp(t/a,σ2)
(15)
其中C=σ2I+ΦA-1ΦT,并以此作为着手点,把边缘似然函数分解成两部分:
(16)

通过极值定理可知,当∂i取如下的值时,可以让l(∂i)达到最大值:
(17)
(18)
当∂i使每一个l(∂i)都取最大值的时候,那么对应的a=[∂1,∂2,…,∂2KL]T就是使边缘似然函数取最大值的超参数。
通过以上分析,快速贝叶斯压缩感知算法的本质就是根据公式(17)(18),使边缘似然函L(a,σ2)最大化。操作步骤如下:
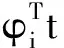
(2)计算均值向量μ和协方差矩阵∑和所有投影向量对应hi和qi。

(4)根据公式(11)(12)(14)重新计算μ,∑,σ2,hi和qi的值,并返回第三步,直到两次的迭代结果小于门限值或迭代次数超过一定范围,退出循环。
贝叶斯压缩感知与其他算法的不同之处在于所求得的稀疏系数最终表现为某概率密度函数的形式。例如本文的稀疏系数为均值向量是μ和协方差矩阵是∑的多元正态分布,因此可以认为均值向量就是对应的稀疏系数,而且可以将协方差矩阵作为误差棒来刻画稀疏系数的准确程度。
4 仿真实验及结果
在这部分,我们对BCS成像算法进行了仿真,并分别采用基追踪算法(BP)、正交匹配追踪算法(OMP)及BCS算法重构稀疏目标。以验证BCS算法的性能表现。BP算法是将凸优化问题转化为线性规划(Linear Programming)问题求解[15]。信号重建误差小、精度高,但相对比较复杂,计算复杂度较高,重建速度比较慢。OMP算法为基于l0范数的贪婪算法中的匹配追踪系列算法,它是基于信号稀疏分解而构造的一类算法[16]。这类算法的计算简单、速度较快,但是信号重建效果较差。
在仿真中,假设系统发射电磁波的起始频率f0=1 GHz,最高频率fN-1=3 GHz,频率步进点数N=101,天线测量位置总数M=30,信噪比为10 dB。三个目标点的深度和水平位置坐标分别为(40,10)、(40,20)、(40,30)(单位cm)。不考虑地面回波的影响下,成像区域沿水平方向从1 cm到40 cm,沿深度方向从30 cm到50 cm。成像区域被均匀地划分为21×40个大小为1 cm的网格目标,成像结果如图3所示。
通过表1对比可以看出OMP算法的速度最快,BP 算法的速度最慢。这主要是由算法本身的性能造成的:BCS 算法和 BP 算法在每次迭代时都需要计算矩阵的逆,这使得它们需要更多的运算时间,但是BCS 方法能够更快地收敛,因此速度明显比 BP算法更快;OMP 算法每次迭代的主要步骤是计算残差与采样矩阵的内积,且迭代次数主要取决于重构目标的稀疏度,因此其速度最快。对于各种算法的重构精度,从图中可以看出,在信噪比为10 dB时,BP和BCS的重构精度相近,但是BP所消耗的时间最长;OMP的恢复精度较差。
图4为在信噪比为10 dB的条件下,测量个数与算法运行时间的关系,可以看出随着测量点的增加,算法运行时间也不断增加。

从图5可以看出随着测量点的增加,三种算法的均方误差都有变小的趋势,其中BP算法的均方误差值要比BCS算法的小一些,但相差不多,BP算法和BCS算法的均方误差要明显小于OMP算法。

图3 当信噪比为10 dB时,各算法的重构结果

对比算法OMPBPBCS时间(s)0 03135 110 13
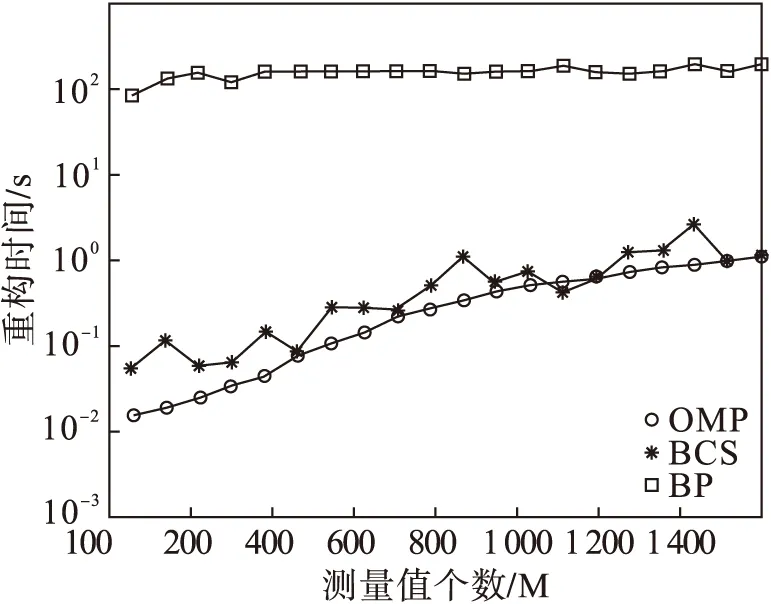
图4 测量个数对重构时间的影响
图6所示为当采样点为450时,噪声对各种算法性能的影响。可以看出,当噪声较大对,BCS算法的重构效果较差,不过当信噪比大于10dB之后,BCS算法与OMP算法的重构效果相近,且要好于BP算法。
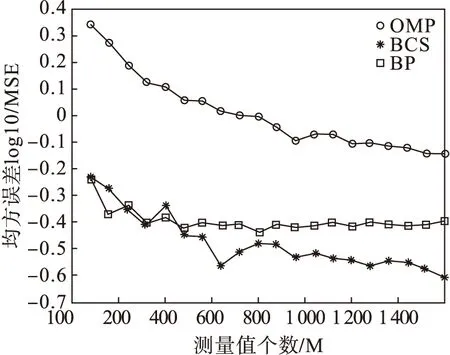
图5 测量个数对重建均方误差的影响
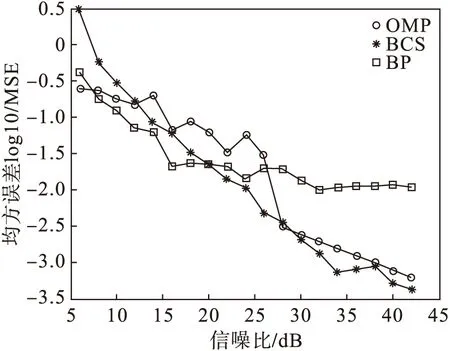
图6 噪声对均方误差的影响
5 结论
本文主要介绍了一种基于稀疏贝叶斯学习的贝叶斯压缩感知频率步进探地雷达成像重建算法,所提成像算法采用分层贝叶斯模型,能够从较少的压缩采样数据中重建目标的位置和反射系数。仿真结果表明,相比其他的经典算法,所提成像算法能够更好地利用探测场景的统计先验信息,更好地兼顾重构精度和计算效率。本文虽然将贝叶斯压缩感知的方法应用到复数域,不过模型中复数的实部和虚部并不是相互独立的,采用何种建模能更精确的体现目标的稀疏特性,将是今后研究的方向。
[1]T Counts,C Gurbuz.W R Scott.Multistatic ground penetra-ting radar experiments[J].IEEE Transactions on Geoscience and Remote Sensing,2007,45(8):2544-2553.
[2]D L Donoho.Compressed sensing[J].IEEE Transactionson Information Theory,2006,52(4):1289-1306.
[3]S Ji,Y Xue,L Carin.Bayesian compressive sensing[J].IEEE Transactions on Signal Processing,2008,56(6):2346-2356.
[4]杨海蓉,张成,丁大为,等.压缩传感理论与重构算法[J].电子学报,2011,39(1):142-148.
[5]方红,王年,章权兵.基于稀疏贝叶斯学习的图像重建方法[J].中国图象图形学报,2009,14(6):1064-1069.
[6]D L Donoho,M A Saunders.Atomic decomposition by basis pursuit[J].SIAM Journal on Scientific Computing,1998,20(1):33-61.
[7]白凌云,梁志毅,徐志军.基于压缩感知信号重建的自适应正交多匹配追踪算法[J].计算机应用研究,2011,28(11):4060-4063.
[8]V N Vapnik.Statistical learning theory[M].Wiley,1998.
[9]S D Babacan,R Monila.Bayesian compressive sensing using Laplace priors[J].IEEE Transactions on Image Processing,2010,19(1):53-63.
[10]茆诗松.贝叶斯统计[M].北京:中国统计出版社,1999.
[11]屈乐乐,方广有,杨天虹.压缩感知理论在频率步进探地雷达偏移成像中的应用[J].电子与信息学报,2011,33(1):21-26.
[12]徐建平,皮亦鸣,曹宗杰.基于贝叶斯压缩感知的合成孔径雷达高分辨成像[J].电子与信息学报,2011,33(12):2864-2868.
[13]C Cortes,N Vapnik.Support vector networks[J].Machine Learning,1995,20(3):273-297.
[14]M E Tipping,A C Faul.Fast marginal likelihood maximization for sparse Bayesian models[C].Proceedings of the Ninth International Work-shop onArtificial Intelligence and Statistics.Key West,FL,2003.
[15]李少东,杨军,胡国旗.一种改进的压缩感知信号重构算法[J].信号处理,2012,28(5):744-749.
[16]J A Tropp,A C Gilbert.Signal recovery from randommeasurements via orthogonal matching pursuit[J].IEEE Transactions on Information Theory,2007,53(12):4655-4666.
[17]郭鹏.基于贝叶斯压缩感知的自适应测量算法[J].计算机工程与应用,2013,49(9):200-203.
[18]Candes E J,Romberg J,Tao T.Robust uncer-tainty principles:exact signal reconstruction from highly incomplete frequency information[J].IEEE Transactions on Information Theory,2006,52(2):489-509.
(责任编辑:刘划 英文审校:林嘉)
Stepped-frequency GPR imaging algorithm based on bayesian compressive sensing
SUN Yan-peng,WANG Yi-lin,QU Le-le
(College of Electronic and Information Engineering,Shenyang Aerospace University,Shenyang 110136,China)
The stepped-frequency ground penetrating radar(GPR) based on the traditional compressive sensing is rather computationally intensive and sensitive to the regularization parameter.To solve the above problem,animaging algorithm based on Bayesian compressive sensing(BCS) is proposed in the paper.Within the sparse Bayesian linear regression model,the proposed BCS-based imaging algorithm uses the relevance vector machine to reconstruct the reflectivity of the investigation scene.The numerical simulation results show that the proposed imaging algorithm can take advantage of the prior statistical information of the scene reflectivies and achieve both reconstruction accuracy and computation efficiency compared with the traditional CS-based imaging methods.
stepped-frequency ground penetrating radar;Bayesian compressive sensing;imaging algorithm
2015-07-16
国家自然科学基金(项目编号:61302172),辽宁省自然科学基金(项目编号:2014024002),辽宁省博士启动基金(项目编号:20121035)
孙延鹏(1973-),男,山东茌平人,教授,主要研究方向:航空电子信息系统,E-mail:syp@syiae.edu.cn。
2095-1248(2015)05-0068-06
TN958
A
10.3969/j.issn.2095-1248.2015.05.010
信息科学与工程
