冲击载荷作用下约束阻尼结构振动和声辐射特性研究
2015-05-18张彩霞沙云东
张彩霞,沙云东
(沈阳航空航天大学 a.能源与环境学院;b.航空航天工程学部(院),沈阳 110136)
冲击载荷作用下约束阻尼结构振动和声辐射特性研究
张彩霞a,沙云东b
(沈阳航空航天大学 a.能源与环境学院;b.航空航天工程学部(院),沈阳 110136)
利用部分敷设约束阻尼减小振动和噪声辐射对冲击载荷作用下薄壁板的结构振动和声辐射特性进行了研究。对一四边简支矩形板施加同峰值的三角和半周期正弦形的冲击载荷,通过对时域振动速度、振动速度功率谱密度和声辐射功率级的求解,研究两种载荷对结构振动和噪声辐射的影响。然后在板表面中心位置部分敷设约束阻尼并逐渐增加敷设面积,研究敷设面积大小对减振降噪的影响。结果表明,同峰值的半周期正弦形冲击载荷使结构产生更大的振动及噪声辐射;敷设约束阻尼面积越大结构声辐射功率级越小,但面积逐渐增大,噪声的衰减率却逐渐变小。
冲击载荷;薄壁结构;约束阻尼;减振降噪
薄壁结构在航空航天领域应用广泛,如飞行器蒙皮、发动机燃烧室等。它们常常受到随时间变化的冲击载荷作用而产生强烈的结构振动并辐射较大的噪声,缩短工件寿命、影响工作人员健康。因此对冲击载荷作用下航空薄壁结构的减振降噪研究具有重要意义。粘弹性材料具有大阻尼特性,可以很好地抑制结构产生的振动和噪声,因此阻尼减振降噪技术被广泛应用于机械结构的振动和噪声控制领域[1-7]。约束阻尼的减振降噪效果往往要优于自由阻尼,因此国内外的学者更专注于对约束阻尼减振降噪技术的研究[3-7]。李恩奇等[8]根据 Hamilton原理推导出了约束层阻尼梁运动和边界条件方程,经 Laplace 变换后再引入状态向量,建立系统的空间状态方程。李九天等[9]基于分布参数传递函数的方法研究了粘弹性材料随机性对约束层阻尼结构动力学特性的影响。梁超锋等[10]由材料阻尼的损耗因子出发推导得到了约束阻尼弹性阶段内结构的阻尼矩阵。Theofanis等[11]用有限元的方法计算了粘弹性夹层板的阻尼,并预测了结构的固有频率、模态振型和模态损耗因子,最后研究了粘弹性层和约束层厚度对损耗因子和固有频率的影响。Y.S.Chen等[12]通过实验对约束阻尼夹层结构的损耗因子进行了研究,观察到了温度和频率的变化对损耗因子的影响。
本文对一四边简支的矩形板分别施加同峰值的三角和半周期正弦形冲击载荷,通过完全瞬态分析法求解板表面的时域振动速度和振动速度功率谱密度,观察它们在时域和频域的振动特性及能量分布的差异,再采用耦合有限元和边界元方法求解它们的声辐射功率级。然后在板表面中心位置部分敷设约束阻尼并逐渐增加敷设面积,研究敷设面积大小对减振降噪的影响。
1 结构振动及声辐射理论
1.1 耦合有限元和间接边界元分析
在物理坐标系下,耦合有限元和间接边界元矩阵方程为[13]
(1)
式中,Ks是结构刚度矩阵,Ms是结构质量矩阵,Cs是结构的阻尼矩阵,C是几何耦合矩阵,H(ω)是间接边界元影响矩阵,u是节点位移,μ是节点压力跳动,Fs是结构激励向量,FA是流体激励向量。
1.2 结构声辐射理论
流体是连续的介质,因此认为结构表面振动速度和结构表面流体的振动速度相同[14]。若结构表面任意一点的声压为P(y,ω),那么
(2)
式中,ρ是空气密度,r是结构表面任意两点x和y间的距离,c是声速。结构表面的声强可以表示为
(3)
式中,Re是雷诺数,T是时间。结构表面声辐射功率的表达式为
(4)
2 冲击载荷算例
2.1 不同冲击载荷下的响应
研究对象为一四边简支的矩形薄板,长、宽和高分别为1 000 mm、600 mm和3 mm,材料密度为1 763 kg/m3,泊松比为0.32,杨氏模量为73.11 GPa,几何模型如图1所示。有限元模型采用shell181单元。对薄板进行模态分析得到前8阶振动频率如表1所示。
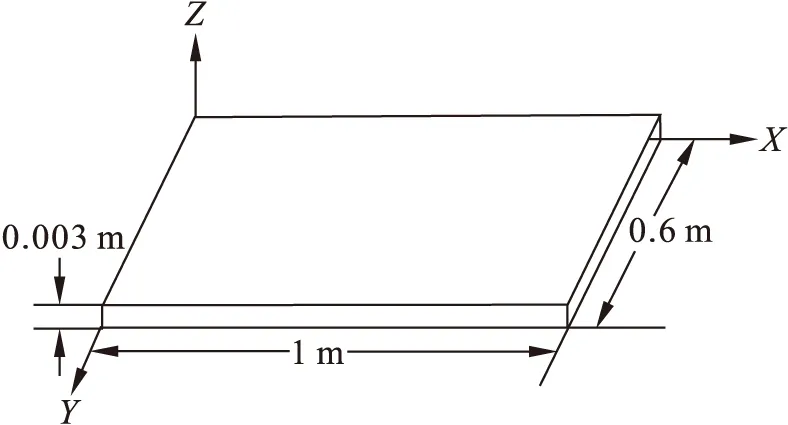
图1 薄板几何模型
通常采用矩形、三角形和半周期正弦形载荷模拟冲击载荷进行研究[15],本文选择后两者。在板的中心位置分别施加峰值为100 N竖直向下的三角和半周期正弦2种形式的冲击载荷,如图2所示,加载时间为0.5 s。利用完全瞬态分析方法得到板表面随时间变化的振动速度,求振动速度的功率谱密度,最后以板表面频域振动速度为边界条件构造模型,在距离结构1 m处建立平面声场网格,对薄板声学响应进行求解。图3~5为薄板中心点振动及声辐射情况,图6为声场云图。

表1 薄板前8阶模态频率

图2 两种形式载荷时域曲线图

图3 薄板中心点的振动速度时域曲线

图4 薄板中心点的速度功率谱密度

图5 薄板中心点的声功率级

图6 两种形式载荷下声场云图
对比发现:(1)载荷加载0.5 s到1 s过程中,三角形载荷的振动速度可以分为正向和负向两个阶段,在峰值处发生变换,在各阶段内振动速度变化较小。半周期正弦形载荷的振动速度在正向到负向变化过程中出现中间阶段,即正负向交替出现。自由振动1 s后阶段,半周期正弦形载荷的起始振动速度较大、衰减较快;(2)薄板施加半周期正弦形冲击载荷后振动能量主要集中在特征频率处,而施加三角形冲击载荷后在各频率处能量分布比较均匀,载荷形式的改变并没有改变结构的特征频率;(3)半周期正弦冲击载荷声辐射明显大于三角形冲击载荷,同时对环境造成污染的噪声主要集中在低频率处;(4)由声场云图可以发现距离载荷点越近的场点声压越大,并且相同场点施加半周期正弦形冲击载荷时声压较大。可以发现,施加同峰值半周期正弦形冲击载荷后薄板的振动更剧烈,对环境造成的噪声污染问题更为突出,下面主要针对半周期正弦形的冲击载荷进行研究。
2.2 敷设不同面积约束阻尼
在薄板的中心位置敷设不同面积的约束阻尼层,设计覆盖面积分别为6.67%、13.33%和26.67%,如图7所示。
有限元模型层与层之间采用节点共用的方法,基层和约束层分别采用向上、向下偏心的shell181单元,粘弹性层采用solid185单元,厚度分别为3 mm和15 mm。粘弹性层材料属性为杨氏模量270 MPa,损耗因子0.1,泊松比0.49,密度1 780 kg/m3,不考虑粘弹性材料的弹性模量和损耗因子受频率和温度的影响,取经验值。施加图2(b)所示的半周期正弦形冲击载荷。敷设不同面积的约束阻尼后,结构的模态频率如表2所示。薄板中心点时域振动速度曲线和振动速度功率谱密度如图8和图9所示。声辐射功率级曲线和距薄板1 m处平面声场云图如图10和图11所示。

图7 部分敷设约束阻尼几何示意图

Hz

图8 中心点振动速度时域曲线

图9 中心点振动速度功率谱密度

图10 中心点辐射声功率级

图11 约束阻尼不同敷设面积声场云图
研究发现,低频范围内敷设约束阻尼面积越大结构的模态频率越大。敷设面积增大,结构时域振动速度随之减小,但振动速度趋势并无变化。敷设面积从6.67%增加到26.67%时,在100 Hz频率范围内减小了一阶模态频率,声辐射功率级降低了10 dB,减振效果明显;敷设6.67%面积的约束阻尼层后结构声辐射功率级从127 dB降到110 dB;当敷设面积为6.67%时声辐射功率级为110 dB,敷设面积增加一倍声辐射功率级减小了5 dB;敷设面积增加三倍声辐射功率级减小了10 dB。可以发现,敷设面积越大结构声辐射功率级越小,但面积逐渐增大,噪声的衰减率却逐渐变小。由图11可以清楚地看到随着敷设面积的增加相同场点的声压逐渐减小。
3 结论
通过以上研究得出如下结论:
(1)同峰值的半周期正弦形冲击载荷与三角形载荷相比,前者在时域内结构振动速度振幅较大,在频域内振动能量分布更为集中,主要在特征频率处,且结构产生的声辐射功率更强。
(2)冲击载荷下薄壁结构振动能量和噪声辐射主要集中在低频范围内,因此针对冲击载荷下薄壁结构的减振降噪应该关注对低频范围的研究。
(3)敷设约束阻尼面积越大结构声辐射功率级越小,但面积逐渐增大,噪声的衰减率却逐渐变小。因此,工程中敷设约束阻尼的面积应适当,过大的面积可能造成材料浪费,但是得到的减振效果却并不明显。
[1]Xisheng Cao,Hans Peter Mlejnek.Computational prediction and redesign for viscoelastically damped structures[J].Computer Methods in Appllied Mechanics and Engineering,1995(125):1-16.
[2]Semyung Wand,Jeawon Lee.Acoustic design sensitivity analysis and optimization for reduced exterior noise[J].AIAA Journal,2001,39(4):1237-1245.
[3]Mohammed A,Al Ajmi,Khaled A,et al.Graded finite element modeling of constrained layer damping treatments with functionally graded[J].Journal of Intelligent Material Systems and Structures,2008(19):469-474.
[4]R Moreira,J D Rodrigues.Constrained damping layer treatments:finite element modeling[J].Journal of Vibration And Control,2004(10):575-595.
[5]H Zheng,X M Tan,C Cai.Damping analysis of beams covered with multiple PCLD patches[J].International Journal of Mechanical Sciences,2006(48):1371-1383.
[6]Douglas Be,Yang J C S.Transverse compressional damping in the vibratory response of elastic-viscoelastic beams[J].AIAA Journal,1978(16):925-930.
[7]Marcelin J L,Trompette P,Smati A.Optimal constrained layer damping with partial coverage[J].Finite Elements in Analysis and Design,1992(12):273-280.
[8]李恩奇,唐国金,李道奎,等.局部覆盖约束层阻尼梁动力学问题的解析解.振动与冲击,2007,26(5):85-89.
[9]李九天,唐国金,李恩奇,等.粘弹性材料参数随机性对 PCLD 板动力学特性的影响[J].强度与环境,2008,35(1):21-28.
[10]梁超锋,欧进萍.结构阻尼与材料阻尼的关系[J].地震工程与工程振动,2006,26(1):49-52.
[11]Theofanis S,Plagianakos,Dimitris A,et al.High order layerwise mechanics and finite element for the damped dynamic characteristics of sandwich composite beams[J].International Journal of Solids and Structures,2004(41):6853-6871.
[12]Y S Chen,T J Hsu,S I Chen.Vibration damping characteristics of laminated steel sheet[J].Metallurgical and Materials Transactions A,1991(22A):653-656.
[13]徐张明 沈荣瀛 华宏星.利用FEM/IBEM计算流体介质中的壳体的结构声耦合问题[J].振动工程学报,2002,15(3):363-367.
[14]伊岗,陈花玲,陈天宁.薄板低频声辐射效率的研究[J].西安交通大学学报,1999,33(3):108-110.
[15]张涛,刘土光,赵耀,等.加筋板弹性大挠度的冲击响应分析[J].爆炸与冲击,2002,22(4):301-307.
(责任编辑:宋丽萍 英文审校:隋华)
Vibration and sound radiation analysis of plates with constrained layer damping patches under impact loading
ZHANG Cai-xiaa,SHA Yun-dongb
(a.College of Energy and Environment;b.Faculty of Aerospace Engineering,Shenyang Aerospace University,Shenyang 110136,China)
The vibration and sound radiation characteristics of thin-walled structure under impact loading were analyzed by applying some constrained layer damping patches to reduce the vibration and noise radiation.Through same volume of triangle and half-cycle sinusoidal impact loading on a simply supported rectangular plate,the vibration velocity,velocity power spectral density and acoustic radiation power levels were studied to find out the effects of these two loadings on vibration and noise radiation.Then the center of the plate was covered with some constrained layer damping patches and the laying area was increased gradually to find out the effect.The results show that the half-cycle sinusoidal impact loading resulted in greater vibration and noise radiation.The larger the constrained area,the smaller the noise radiation,while the noise attenuation rate was gradually getting smaller.
impact loading;thin-walled structure;constrained layer damping;reduction of vibration and noise radiation
2013-11-06
张彩霞(1988-),女,辽宁辽阳人,硕士研究生,主要研究方向:飞行器动力学环境工程及控制技术研究,E-mail:617321997@qq.com;沙云东(1966-),男,黑龙江阿城人,教授,主要研究方向:航空发动机强度,振动及噪声,E-mail:Ydsha2003@vip.sina.com。
2095-1248(2015)05-0037-06
F416.5
A
10.3969/j.issn.2095-1248.2015.05.004
