波动数值模拟的常加速度显式算法

2015-05-17孙明社曲淑英侯兴民

烟台大学学报（自然科学与工程版） 2015年1期

孙明社，曲淑英，侯兴民

(烟台大学土木工程学院，山东烟台 264005)

在土木工程和地震工程领域有很多问题都可以归结为波动问题，如强震地面运动、土－结构相互作用、结构的无损检测与探伤等问题.因而，研究工程波的传播与振动具有非常重要的意义.通过建立力学模型，工程波动问题一般就可转化为偏微分方程的求解.由于实际工程中许多工程结构建立的动力方程为非线性，很难获得精确的解析结果，因而，数值方法便得到广泛应用.时域逐步积分法是结构动力方程求解中的一种有效方法.根据是否需要求解耦联方程组，时域逐步积分法又可分为显式算法和隐式算法.隐式时域逐步积分算法的研究成果较多，如常平均加速度方法、Houblt方法、Newmark方法、Gurtin方法、Wilson-θ方法、Park方法以及 a方法等[1－5].但是随着结构自由度数目的增大，求解耦联方程组的工作量巨大，由于显式时域逐步积分方法无需求解耦联方程组，因而具有明显的优势.廖振鹏、李小军、周正华、侯兴民等[6－20]对显式时域逐步积分算法都进行了研究.本文在国内外学者研究成果的基础上探讨了平均常加速度隐式算法，即通过矩阵级数展开转变为显式算法，最后将该显式算法在工程波动数值模拟中进行应用，并与文献[21]的中心差分算法比较，说明常加速度显式算法可以较好的应用于工程波动数值模拟中.

1 隐式算法显式化推导

1.1 基本方法

对于时域逐步积分方法的广义线性加速度算法，每向前计算一步都需求解耦联线性方程组

式中:M为质量矩阵;C为阻尼矩阵;K为刚度矩阵;{u}i+1为ti+1时刻的位移;{}i+1为ti+1时刻的广义荷载;a，b为常数，不同的加速度取不同的值.

对式(2)矩阵求逆矩阵，有

将式(1)进行矩阵求逆、级数展开、级数截断最终得到式(9)，完成了隐式算法转化为显式算法.式(9)可不必求解耦联线性方程组，提高了计算速度，节省了计算时间.用上述方法，以平均常加速度方法为例，推导其隐式显式化过程，并进行出平面运动的波动数值模拟.

1.2 平均常加速显式化

当Newmark－β逐步积分方法中的参数γ、β取不同值时，该方法退化为平均常加速度法、线性加速度法、中心差分法等.当γ=0.5、β=0.25时，为平均常加速法，即式(1)中的参数取值:a=4，b=2.公式

(1)可记作

将式(10)与式(1)对比，应用前述推导过程，可以得到平均常加速方法对应的显式化公式如下

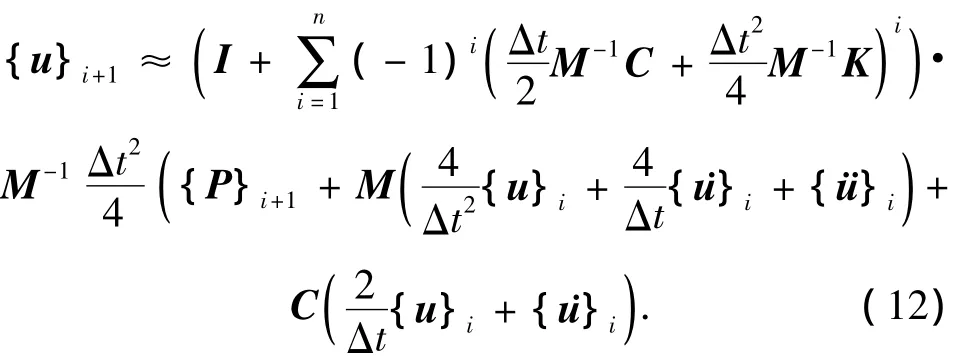
应用式(13)、(14)可以分别得到离散时间点上的速度、加速度

式(12)、(13)、(14)为平均常加速算法的显式化公式，若给定初始时刻的初始位移{u}0、初始速度{˙u}0、初始加速度{¨u}0，即循环使用公式(12)、(13)、(14)，得到所有离散时间点上的位移、速度、加速度.

平均常加速方法显式化的收敛条件，由式(7)可知

取向量的“1”范数，求解上式，可得

对于单自由度无阻尼体系ξ=0，带入上式，得

2 出平面波动数值模拟

2.1 出平面问题

如图1，在直角坐标系oxyz下，弹性半空间内，剪切模量μ1=1，介质密度ρ1=1，不考虑阻尼.波源为沿y轴方向深度hs处作用的暂态荷载:

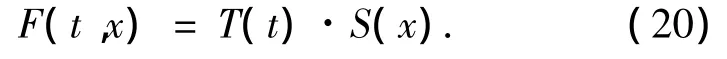
图1 出平面波源问题Fig.1 Problem of out-plane wave

暂态波源荷载时间分布函数为三角形脉冲T(t):

2.2 平面波动数值模拟

波动数值模拟的精度需要将有限单元的尺寸划分的与波长相比足够小，因而在建立动力方程时才可以将每一有限单元内惯性体积力视作不随空间变化的恒定量.为了实现动力方程的空间解耦，采用了集中质量有限元模型.

采用有限单元法将连续弹性半空间介质离散化，用有限个单元组合体代替原本的连续介质.用平面正方形单元将弹性半空间介质离散化，假定各个单元只在公共节点上相互铰接.离散的正方形单元边长即空间离散步长为:Δx=Δy=0.05;单元节点编号如图2;单元刚度[15]如矩阵(23).

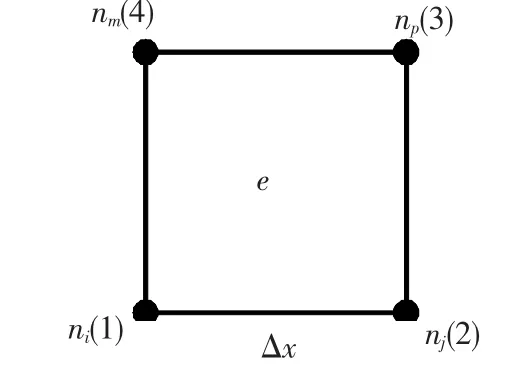
图2 正方形单元节点编号Fig.2 Node number of square unit

将弹性半空间沿y轴向下划分n个网格;y轴左右两侧，沿x轴正负方向各划分m个网格，见图3.

图3 弹性半空间网格离散Fig.3 Discrete mesh of elastic half space

观测点位移峰值如表1.有限元网格划分m=40，n=40;时步 Δt=0.0075 s;暂态波源作用位置hs=0即表面荷载;考虑二阶透射边界.采用Fortran程序语言进行中心差分算法和平均常加速隐式转换显式算法编程计算，取(0，0)(0.5，0)(1.0，0)(0，0.5)(0，1.0)5个观测点，得到暂态波源作用下的弹性半空间计算结果.相同时步下中心差分算法和常加速度显式算法不同观测点的位移曲线如图4.

表1 观测点位移峰值Tab.1 Displacement peak of observation point

图4 观测点位移曲线Fig.4 Displacement curve of observation point

将式(12)中系数逆矩阵取不同展开阶数下的各观测点位移曲线如图5.

图5 不同阶数下的观测点位移曲线Fig.5 Displacement curve of observation point under different order number

3 结论

通过对比中心差分和常加速显式方法的计算结果分析，得到如下结论.

(1)相同的网格数目、时步、边界条件下，2种算法的出平面波动的主要波形完全吻合，峰值相同.曲线后段虽然存在一定的差别，但是，工程中我们主要关注主要波形，因而可以满足工程要求.

(2)考虑阻尼的情况下，中心差分算法的显式优势不明显，而常加速度显式算法仍为高效率的显式算法，具有一定优势.

(3)逆矩阵在单位矩阵处级数展开，阶数不同，但观测点的位移曲线基本重合，说明常加速显式算法只需取前几阶就可满足精度要求，且计算效率较高.

[1]Newmark N M.A method of computation for structural dynamics[J].Proc ASCE，1959，85(3):69－94.

[2]Bathe K J，Wilson E L.Stability and accuracy analysis of direct integration method[J].Earthq Eng and Struct Dynam，1973(1):283－291.

[3]Hiber H M，Hughes T J R，Tayler R L.Improned numerical dissipation for time integration algorithins in structural dynamics[J].Eathq Eng and Struct Dynam，1977，5(3):283－292.

[4]Hiber H M，Hughes T J R.Collocation dissipation and overshoot for time integration schemes in structural dynamics[J].Eathq Eng and Struct Dynam，1978，6(1):99－177.

[5]Subbara J K，Dokainish M A.A survey of direct time integration methods in computational structural dynamics(II)[J].Computers and Structures，1989，32(6):1387－1401.

[6]廖振鹏.近场波动问题的有限元解法[J].地震工程与工程振动，1984，4(2):1－14.

[7]李小军，廖振鹏，杜修力.有阻尼体系动力问题的一种显式差分解法[J].地震工程与工程振动，1992，12(4):74－79.

[8]钟万勰.结构动力方程的精细时程积分法[J].大连理工大学学报，1994，34(2):131－136.

[9]李小军.地震工程中动力方程求解的逐步积分方法[J].工程力学，1996，13(2):110－118.

[10]周正华，李山有，侯兴民.阻尼振动方程的一种显式直接积分方法[J].世界地震工程，1999，15(1):41－44.

[11]杜修力，王进廷.阻尼弹性结构动力计算的显式差分法[J].工程力学，2000，17(5):37－43.

[12]王进廷，杜修力.有阻尼体系动力分析的一种显式差分法[J].工程力学，2002，19(3):109－112.

[13]陈学良，金星，陶夏新.求解加速度反应的显式积分格式研究[J].地震工程与工程振动，2006，26(5):60－67.

[14]高小科，邓子辰，黄永安.基于三次样条插值的精细积分法[J].振动与冲击，2007，26(9):75－82.

[15]廖振鹏，刘恒，谢志南.波动数值模拟的一种显式方法－一维波动[J].力学学报，2009，41(3):350－359.

[16]刘恒，廖振鹏.波动数值模拟的一种显式方法－二维波动[J].力学学报，2010，42(6):1104－1116.

[17]谢志南，廖振鹏.波动方程数值模拟的一种显式方法[J].力学学报，2011，43(1):154－161.