基于旋量方法的高超声速飞行器三维非线性伪最优制导律设计*

彭双春，朱建文，汤国建，陈克俊

(国防科技大学航天科学与工程学院，湖南长沙 410073)

高超声速飞行器采用倾侧转弯(Bank-To-Turn，BTT)方式机动飞行。相对于侧滑转弯(Skid-To-Turn，STT)机动控制方式，BTT控制方式在气动效率、机动能力、控制性能、稳定性能、命中精度等方面具有明显优势［1］，但BTT飞行器通常面临通道间运动耦合作用［2］。对于高超声速飞行器而言，由于在末制导过程中进行的是高速及大空域飞行，通道间的运动耦合作用非常严重。而在大多数制导律的推导过程中，一般都假设飞行器控制系统是稳定的，即飞行器的姿控系统使得飞行器稳定、视线的俯仰和偏航通道相互解耦，却忽略了通道耦合对制导律设计的影响［3－4］。显然在BTT飞行器的实际作战过程中，这种假设是不成立的。因此，需要针对高超声速飞行器的末制导过程构建包含运动耦合信息的制导模型，设计新型三维制导律来避免这种假设的不合理性。

更进一步，在实际应用中，高超声速飞行器制导通常需要获得最佳的制导性能，如脱靶量最小、能量最省、时间最短等，同时，高超声速飞行器的弹道特性对制导参数更加敏感，因此为了保证制导过程中弹道平稳、光滑，需要对制导参数进行优化。从制导的角度来看，为了保证制导信息的完整性，有些学者基于李群［5－6］、微分几何［7－8］、球面几何［9－10］、微分平坦［11］、矢量描述［12－13］等非线性方法进行了制导模型的构建，但这些方法虽然理论完整却不够简洁，因而，制导律的形式复杂，使得对其直接进行参数优化存在很大的难度。通常的做法是在制导律设计完成后，参照基于双平面解耦方法获得的线性最优制导律，完成对制导参数的设定，但这实质上是一种经验方法，缺乏必要的理论支持，不能够从理论上保证制导律具有优良的制导性能。文献［14］中设计了一种能够较好地描述视线方位的飞行器－目标视线矢量的几何旋量，并最终设计了一种考虑制导参数优化的新型三维非线性制导律。

1 制导问题分析

构建如图1所示的飞行器对目标进行俯冲攻击的示意图，目标T固定于坐标系的原点O，r为弹目视线矢量，其长度为r，从目标质心T指向飞行器质心M。M'为M在xoz平面的投影。qd和qt分别为视线高低角和视线方位角，qtt为视线矢量在转弯平面内的方向角。ec，et，ed，er，ett为单位矢量，ec与矢量 OM'同向，et与 y轴同向，er与 r同向，O－eceted构成右手直角坐标系，O－ederett构成右手直角坐标系。飞行器M速度为v，ηd为速度矢量在俯冲平面与转弯平面的夹角，θd为速度矢量在俯冲平面内的方向角;对应地，ηt为速度矢量在转弯平面与俯冲平面的夹角，θt为速度矢量在转弯平面内的方向角。

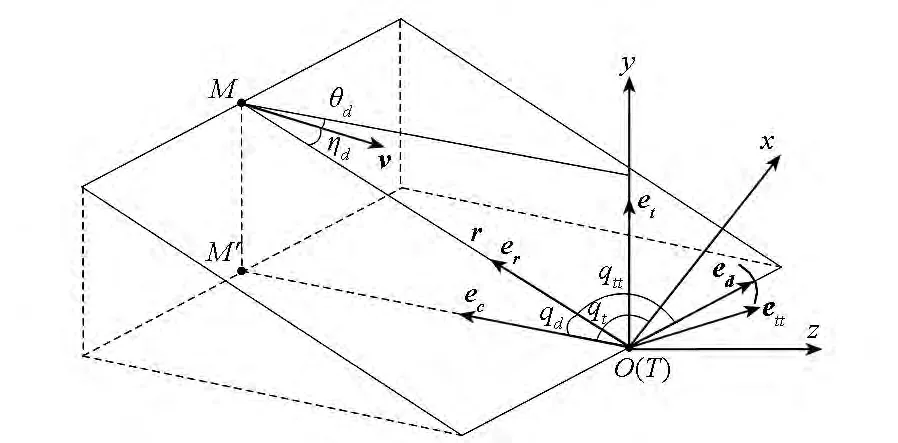
图1 制导模型示意图Fig.1 Sketch map of guidance model

制导问题可以描述为弹目视线方位和视线角速度的控制问题:在飞行器接近目标的过程中，当无终端约束时，制导的目的是使视线转动稳定下来，即控制视线角速度收敛至零(ω→0)，从而实现对目标的瞄准式攻击;而当存在终端视线方位约束时，制导的目的是使视线转动到一个确定的方向，即 qd→qdf、qd→qtf，并保持视线角速度的稳定，即ω→0。

2 视线旋量与视线旋量速度

2.1 旋量的相关定义

为了在保证制导信息完整性的同时简化模型结构，在此参照李群旋量结构［5］，引入角度矢量、视线旋量、视线旋量速度等概念，以实现视线方位和视线角速度的控制。

定义1(角度矢量) 坐标平面内角度值与垂直于所在平面的单位矢量的乘积称为角度矢量，单位矢量的方向由坐标平面内角度值的符号唯一确定(如图1中，qded，qtet分别为视线高低角矢量和视线方位角矢量)。

定义2(视线旋量) 视线高低角矢量和视线方位角矢量的矢量和称为视线旋量，记为σ。

定义3(视线旋量速度) 视线旋量的导数称为视线旋量速度，记为~ω。

根据以上定义，视线旋量可以表达为

视线旋量速度为

视线旋量的引入能够为设计同时满足入射方位角和落角约束的制导律提供便利，同时，从式(1)可知，视线旋量具有明确的物理意义，便于进行制导参数的优化。

2.2 等价性分析

为了说明视线旋量、视线旋量速度控制分别与视线方位、视线角速度控制的一致性，给定如下的等价性定理及证明。

定理1(等价性定理) 视线旋量控制与视线方位控制等价;视线旋量速度控制与视线角速度控制等价。

证明:(Ⅰ)假设 σf=qdfedf+qtfetf，视线旋量控制的目标为σ→σf，则

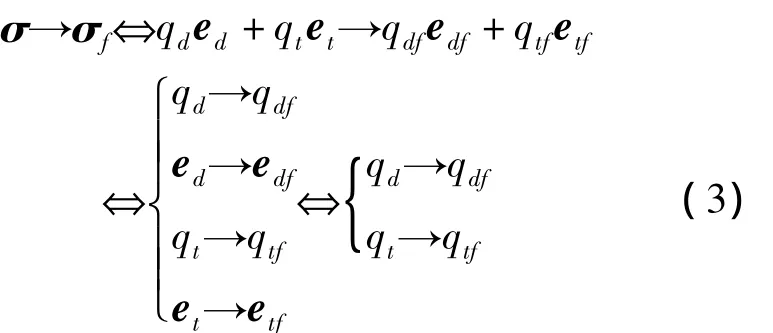
从而视线旋量控制与视线方位控制等价。 □

(Ⅱ)根据定义3，视线旋量速度为

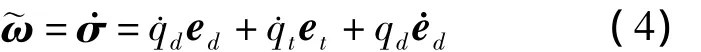
根据视线角速度加法定理［12，15］，飞行器－目标视线角速度矢量ω可以表示为视线高低角速度和视线方位角速度的矢量和，即

视线角速度的控制目标为ω→0，即

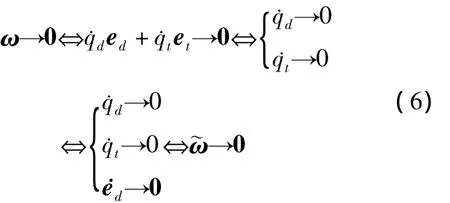
则视线旋量速度控制与视线角速度控制等价。□

综上所述，定理1得证。

基于等价性定理，可以将视线方位和角速度控制问题转化为视线旋量和旋量速度控制问题。

3 三维非线性制导模型构建

对式(4)求导可得视线旋量速度变化模型为

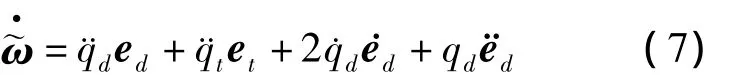
从式(7)可以看出，求解模型的关键是确定参数¨qd，¨qt，˙ed，¨ed的表达式。

1)计算¨qd。设θd＜0，则在俯冲平面内有

由图1可得

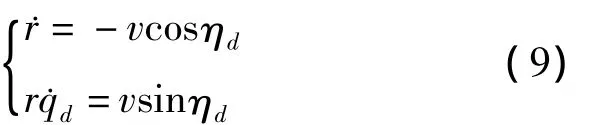
将式(9)中第二式两边同时对时间求导，并将式(8)和式(9)代入，即可得

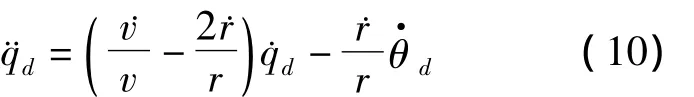
在实际飞行过程中，由于˙v/v≈0，定义Tg=－r/˙r(r＞0)，则式(10)可改写为

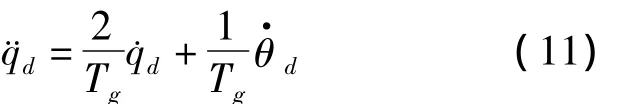
2)计算¨qt。设r1，v1，θt1分别为转弯平面内参数r、v、θt在水平面内的投影分量。同理，在转弯平面的水平投影平面内有

由图1可得

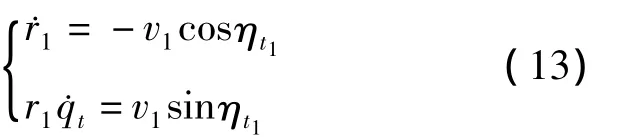
运用与俯冲平面相同的推导方式，可得

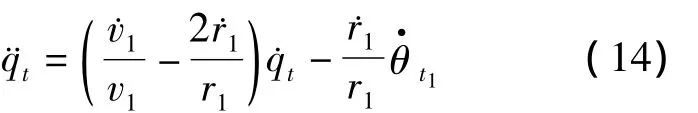
式(14)中，˙v1/v1≈0，r1=rcosqd，则

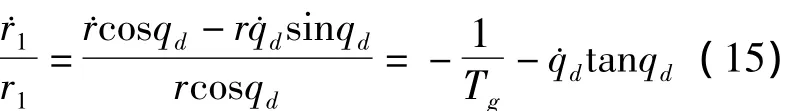
将式(15)代入式(14)得

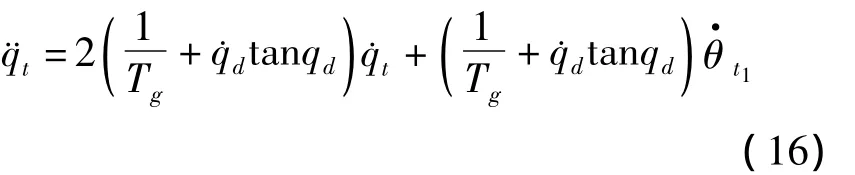
3)计算˙ed，¨ed。根据图1，有

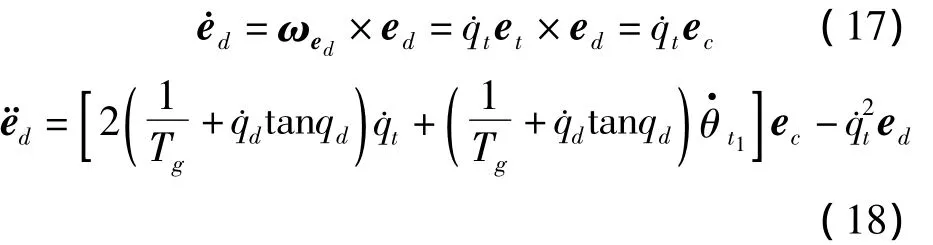
将式(11)、式(15)、式(17)、式(18)代入式(7)，并令u，经整理可得

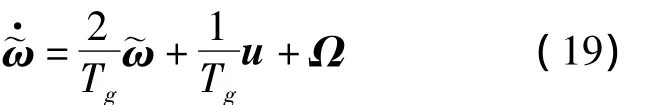
式(19)中，u为控制项，Ω为运动耦合项。在飞行器进行高速大空域机动制导时，Ω将具有较大的值，在制导律设计过程中不可简单忽略。

由此，基于视线旋量和旋量速度，可得三维非线性制导模型为

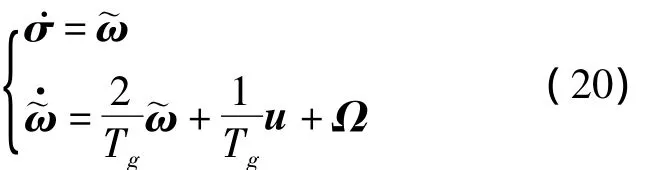
从式(20)可以看出，基于视线旋量和视线旋量速度的模型描述方式较好地分离了控制量和耦合量，从而使得三维非线性制导模型结构相对简单，便于进行后续制导参数优化。

4 三维非线性伪最优制导律设计

从式(20)可以看出:若直接求解最优制导问题，将面临难以克服的Riccati微分方程求解困难，难以获得解析解。引入伪控制变量［6］，将复杂的非线性微分方程转化为线性微分方程，然后进行最优制导律的设计。定义伪控制变量~u为

则模型可以简化为

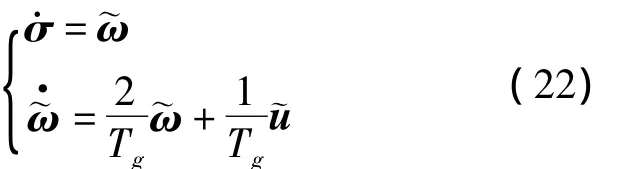
从而，在不损失制导信息的前提下，制导模型转化为线性形式，可以方便地基于二次型最优方法进行三维制导律设计。设计相应的二次型目标函数为

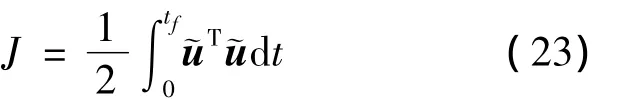
4.1 无终端约束情况

基于等价性定理，无终端约束制导问题可以等价于视线旋量速度趋于零(~ω→0)的问题。取状态变量x=~ω，则可得状态方程

结合目标函数式(23)，根据极大值原理，线性系统二次型性能指标的最优控制为

式中P可由逆Riccati方程求解得到:

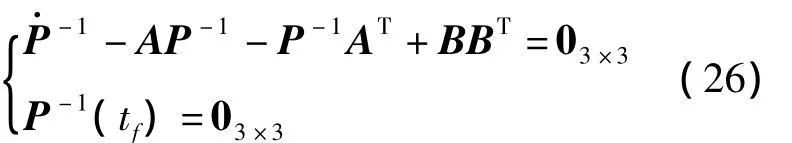
参照参考文献［3］的求解过程，解式(26)得

则

则无终端约束情况下的伪最优三维非线性制导律为

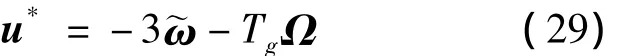
从式(29)可以看出，在忽略耦合补偿项－TgΩ的情况下，式(29)与文献［3］的结论是一致的。

4.2 有终端约束情况

对于有终端约束情况，除了要求视线角速度趋于零外，还要求视线方向转移到一个指定的方位，基于等价性定理，即~ω→0且σ→σf，令

则可得到形如式(24)的状态方程

其中:

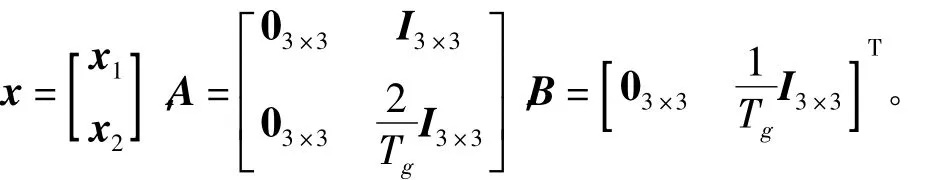
则最优控制为

类似4.1节的推导过程，可得有终端约束情况下经过参数优化的三维非线性制导律为

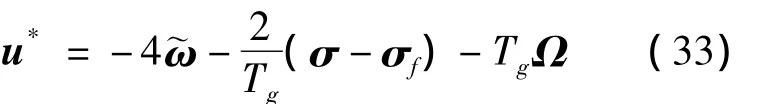
在忽略耦合补偿的情况下，式(33)与文献［3］的结论亦是一致的。

5 仿真验证

为了验证制导律有效性，以某BTT－180型飞行器为对象进行相关验证实验，基本参数设置如表1所示。

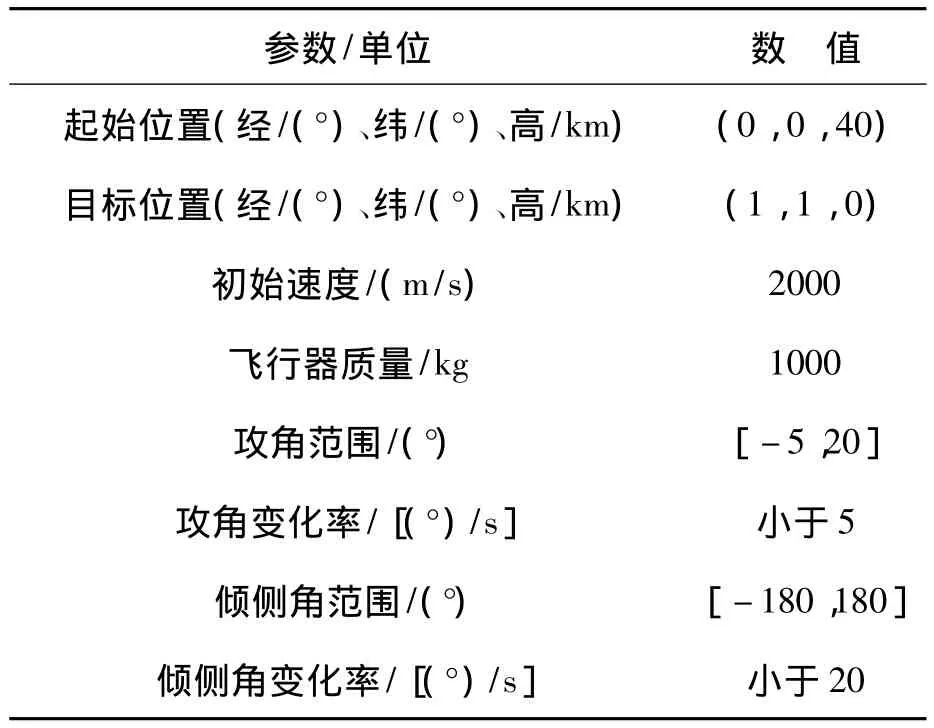
表1 仿真基本参数Tab.1 Basic parameters for simulation

5.1 仿真算例1:无终端约束攻击目标

初始速度方向设为－20°(以正北为基准，逆时针为正)进行仿真实验，飞行器经过112.67s到达目标，弹道平稳光滑，脱靶量为1.29m，得到无终端约束情况下的仿真结果如图2～4所示。从图2可以看出:飞行弹道末段平直，说明在所设计制导律的作用下，飞行器能够实现对目标的瞄准式攻击。从图3和图4可以看出:攻角、倾侧角在整个飞行过程中变化平稳，在飞行末段均收敛为较小值，这说明制导指令是收敛的，制导系统输出的制导指令对通道耦合较好地进行了实时补偿与控制。

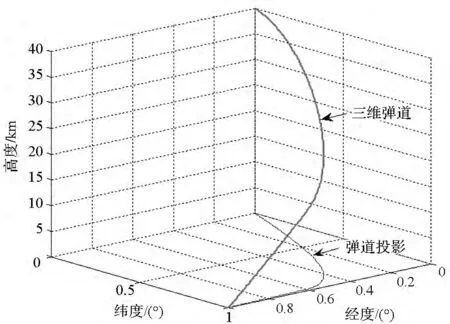
图2 无终端约束弹道(本文方法)Fig.2 Trajectory without ending constraint in the proposed method

忽略耦合项影响，采用传统通道解耦方法［3］来进行相应对比仿真，得到仿真结果如图5～7所示。

飞行器经过111.43s到达目标，脱靶量为10.51m。从仿真结果可以看出:在传统制导律的作用下，飞行器仍保持了较高的制导精度，但当制导指令不对通道耦合进行实时补偿时，飞行弹道末段不再严格收敛，攻角、倾侧角在接近目标时才趋于较小值，这说明传统制导律对弹道的调整效率相对较低，在初始射向与射面具有较大的偏差情况下，传统方法难以实现对目标的瞄准式攻击。

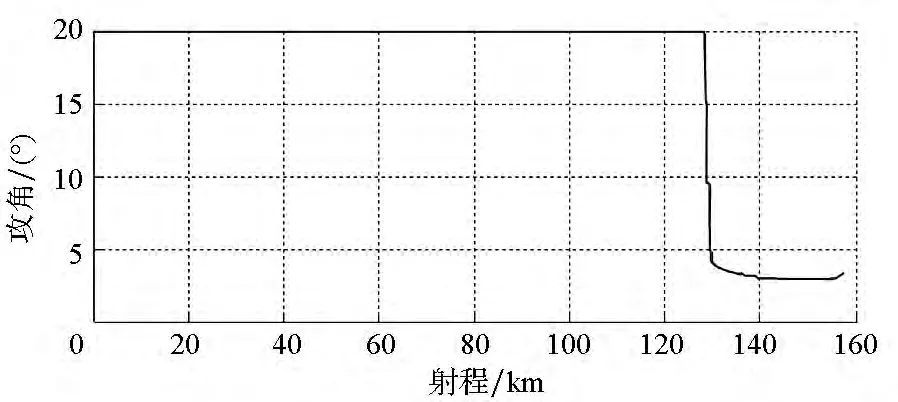
图3 无终端约束下攻角－射程变化曲线(本文方法)Fig.3 Attack angle versus range without ending constraint in proposed method

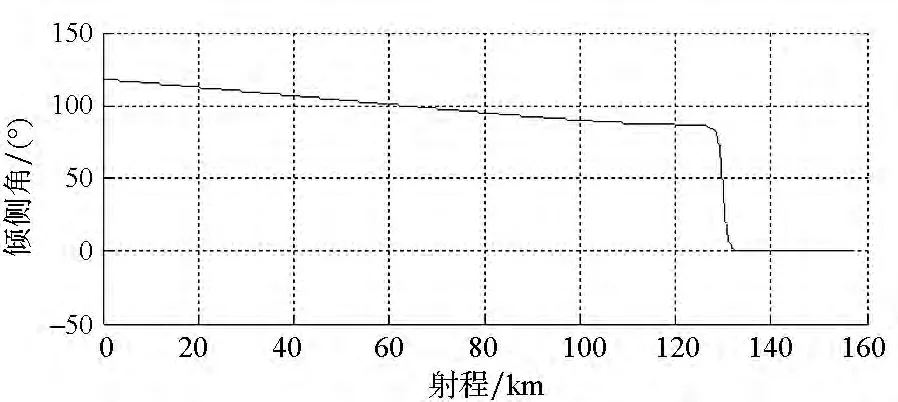
图4 无终端约束下倾侧角－射程变化曲线(本文方法)Fig.4 Bank angle versus range without ending constraint in proposed method

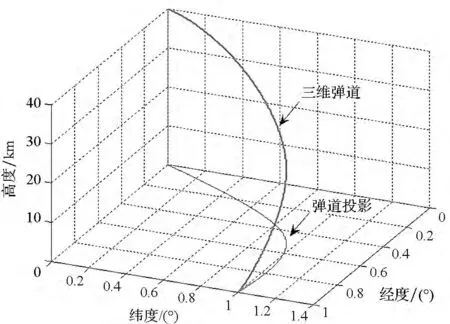
图5 无终端约束弹道(传统方法)Fig.5 Trajectory without ending constraint in traditional method

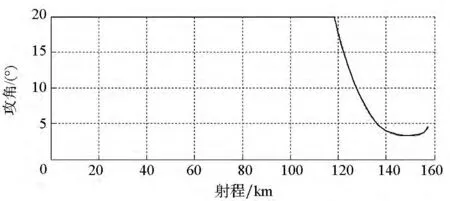
图6 无终端约束下攻角－射程变化曲线(传统方法)Fig.6 Attack angle versus range without ending constraint in traditional method

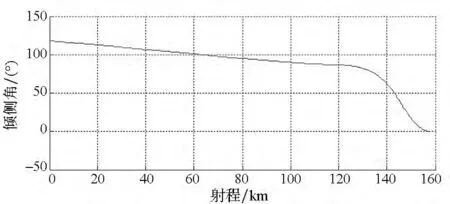
图7 无终端约束下倾侧角－射程变化曲线(传统方法)Fig.7 Bank angle versus range without ending constraint in traditional method

5.2 仿真算例2:有终端约束攻击目标

初始条件同仿真算例1，假设目标位于山谷中，依靠山峰作为天然屏障，为了对目标实施有效攻击，需要避开山峰的障碍、通过设置合适的入射方位角来降低对弹道落角的要求。设预定入射方位角为 －20°，预定落角为 －60°。导弹经过126.51s到达目标，脱靶量为1.33m，实际入射方位角为 － 19.58°，实际落角为 59.98°，基于式(33)所示的制导律，得到的结果如图8～12所示。从图8可以看出:飞行器弹道光滑，有效地避开了山峰的障碍，能够对目标实施有效的“点穴式”打击。从图9、图10可以看出:在有终端约束条件下，弹道能够精确地调整到期望的速度倾角和方位角，从而满足同时存在入射方位角和落角约束情况下的制导需求。从图11、图12可以看出:制导指令变化比较平稳，末端攻角、倾侧角收敛，这说明，飞行器在本文制导方法的作用下，通道耦合得到了较好的实时补偿控制，不再影响制导系统的鲁棒性。

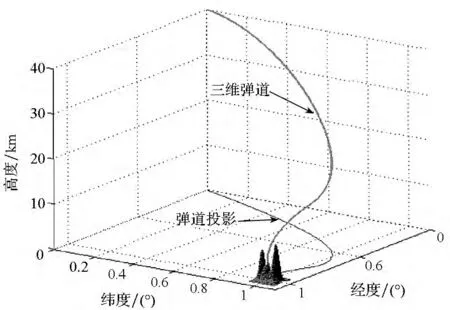
图8 有终端约束弹道(本文方法)Fig.8 Trajectory with ending constraints in proposed method

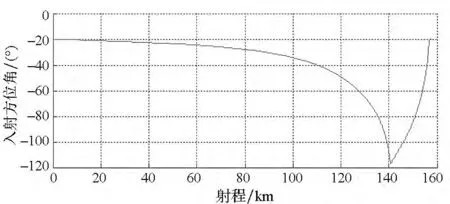
图9 有终端约束下入射方位角－射程变化曲线(本文方法)Fig.9 Incident azimuth angle versus range with ending constraints in proposed method

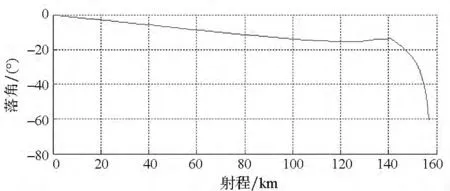
图10 有终端约束下落角－射程变化曲线(本文方法)Fig.10 Impact angle versus range with ending constraints in proposed method

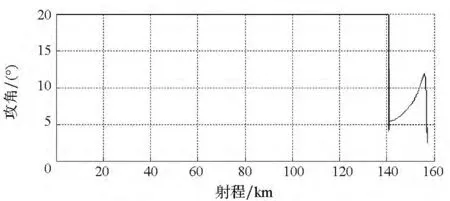
图11 有终端约束下攻角－射程变化曲线(本文方法)Fig.11 Attack angle versus range with ending constraints in proposed method

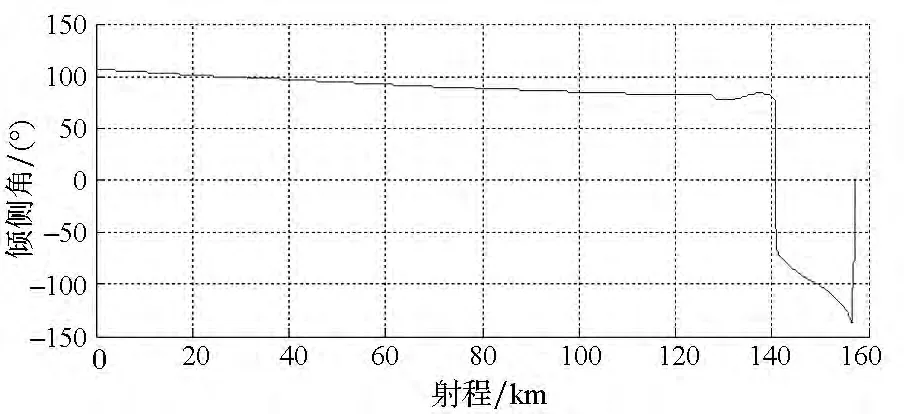
图12 有终端约束下倾侧角－射程变化曲线(本文方法)Fig.12 Bank angle versus range with ending constraints in proposed method

在同样背景下，采用传统解耦方法进行对比仿真。考虑到传统方法不具备按预定入射方位角攻击目标的能力［3］，而为了避开山峰的障碍，设预定落角为 －85°。通过仿真，飞行器经过177.05s到达目标，脱靶量为11.53m，终端落角为－82.99°，得到的结果如图13～16所示。

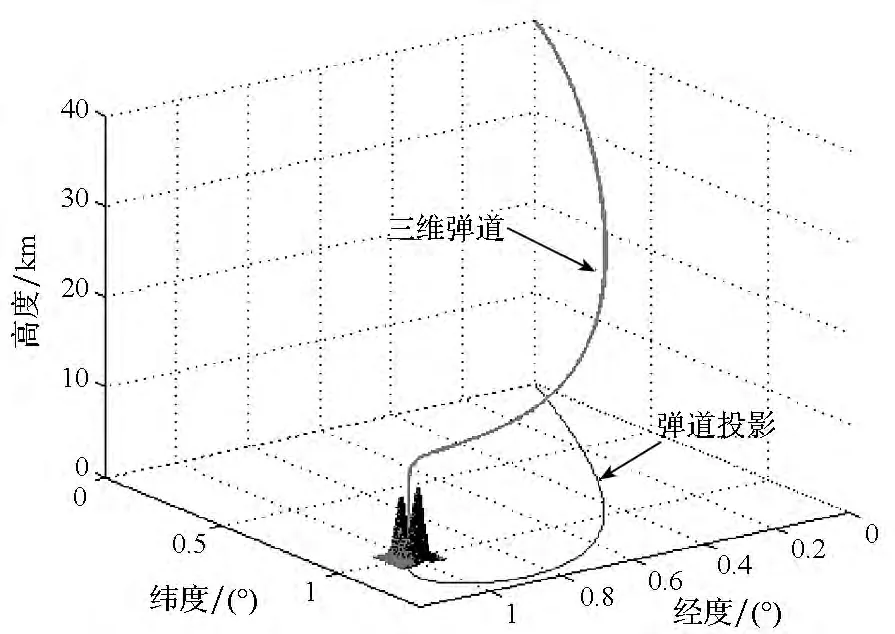
图13 有终端约束弹道(传统方法)Fig.13 Trajectory with ending constraints in traditional method

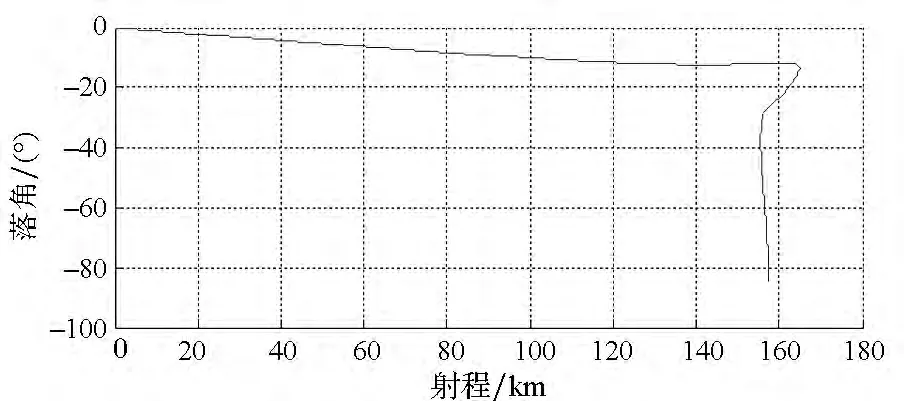
图14 有终端约束下落角－射程变化曲线(传统方法)Fig.14 Impact angle versus range with ending constraints in traditional method

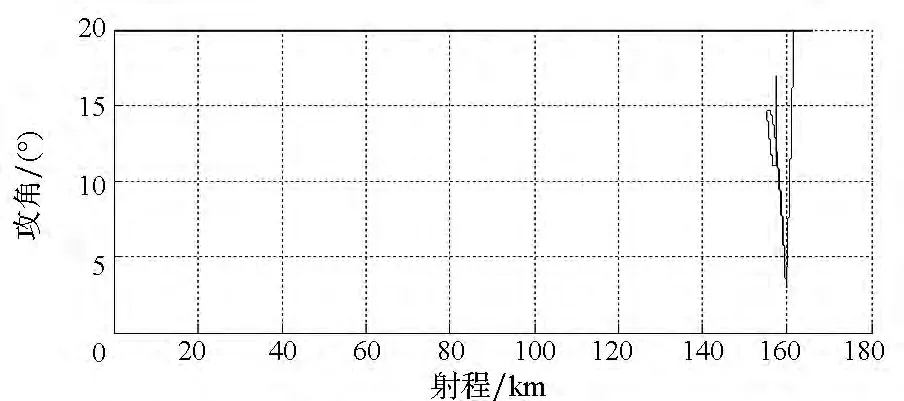
图15 有终端约束下攻角－射程变化曲线(传统方法)Fig.15 Attack angle versus range with ending constraints in traditional method

图16 有终端约束下倾侧角－射程变化曲线(传统方法)Fig.16 Bank angle versus range with ending constraints in traditional method

从图15、图16可以看出:在飞行器接近目标时，制导指令发散，这会影响到制导的稳定性，甚至可能导致脱靶。仿真结果表明:通道耦合对制导系统的影响显著，需要对其进行实时补偿。

6 结论

面向高超声速飞行器末制导过程中的运动耦合问题，基于旋量方法进行了三维非线性伪最优制导律的设计。该制导律的设计具有以下几点意义:

1)该制导律对通道耦合进行了补偿，避免了传统解耦方法带来的制导信息损失，保证了制导信息的完整，在理论上具有较高的制导精度;

2)该制导律能够适应同时存在入射方位角和落角约束的情况，降低飞行器制导对落角的控制需求，同时也可以选择目标最薄弱部位进行有效攻击;

3)该制导律对制导参数行了优化，保证了制导参数的“伪最优”性能，能够提高制导性能。

需要说明的是:高超声速飞行器在实际制导过程中，其飞控系统不可避免地受到各种扰动的影响，导引头/惯导系统的制导信息的测量、传输与估计存在偏差和噪声，目标机动也常常被看成是未知的有界扰动，在这些干扰和摄动的作用下，制导系统参数存在较大的不确定性，这将降低制导律的稳定性和鲁棒性，影响高超声速飞行器的制导效果，甚至导致飞行器失稳和脱靶。在下一步工作中，将重点针对参数扰动问题，基于鲁棒控制理论，研究设计三维非线性自适应制导律，进一步提高制导系统的稳定性。

References)

［1］ Reichert R T.Homing performance comparison of selected airframe configurations using skid-to-turn and bank-to-turn steering policies［R］.NationalAeronautics and Space Administration，1981.

［2］ 佘文学，周凤岐.三维非线性变结构寻的制导律［J］.宇航学报，2004，25(6):681－685.SHE Wenxue，ZHOU Fengqi.High precision 3D nonlinear variable structure guidance law for homing missile［J］.Journal of Astronautics，2004，25(6):681 － 685.(in Chinese)

［3］ 陈克俊，赵汉元.一种适用于攻击地面固定目标的最优再入机动制导律［J］.宇航学报，1994，15(1):1－7.CHEN Kejun，ZHAO Hanyuan.An optimal guidance law of maneuvering reentry vehicle attacking ground fixed targets［J］.Journal of Astronautics，1994，15(1):1 －7.(in Chinese)

［4］ 徐明亮，刘鲁华，汤国建，等.高超声速临近空间飞行器铰链力矩最小俯冲弹道设计［J］.弹道学报，2011，23(3):1－6.XU Mingliang，LIU Luhua，TANG Guojian，et al.Design of dive trajectory of hypersonic near-space vehicle with minimum hinge moment［J］.Journal of Ballistics，2011，23(3):1 －6.(in Chinese)

［5］ 韩大鹏，孙未蒙，郑志强，等.一种基于李群方法的新型三维制导律设计［J］.航空学报，2009，30(3):468－475.HAN Dapeng，SUN Weimeng，ZHEN Zhiqiang，et al.A new 3D guidance law based on a lie-group method［J］.Acta Aeronautica et Astronautica Sinica，2009，30(3):468 －475.(in Chinese)

［6］ 韩大鹏，韦庆，杨乐平，等.任务空间实时轨迹规划的旋量方法［J］.机器人，2008，30(4):304－310.HAN Dapeng，WEI Qing，YANG Leping，et al.A twist-based method for real-time trajectory planning in task space［J］.Robot，2008，30(4):304 －310.(in Chinese)

［7］ Kuo C Y，Chiou Y C.Geometric analysis of missiles guidance command［J］. IEEE Proceedings—ControlTheoryand Applications，2000，147(2):205 －211.

［8］ 张友安，胡云安，苏身榜.三维制导的几何方法与鲁棒控制方法［J］.航空学报，2002，23(1):88－90.ZHANG Youan， HU Yunan， SU Shenbang. Geometric approach and robust control approach to three-dimensional missile guidance［J］.Acta Aeronautica et Astronautica Sinica，2002，23(1):88－90.(in Chinese)

［9］ Han Y H，Xu B.Variable structure guidance law for attacking surface maneuver targets［J］.Journal of Systems Engineering and Electronics，2008，19(2):337 －341.

［10］ 史小平，常莹莹.非线性三维自适应模糊变结构制导规律的研究［J］.宇航学报，2009，30(6):2171－2175.SHI Xiaoping，CHANG Yingying.Study on nonlinear threedimensional adaptive fuzzy variable structure guidance law［J］.Journal of Astronautics，2009，30(6):2171 －2175.(in Chinese)

［11］ 韩大鹏，孙未蒙，郑志强，等.基于微分平坦方法的三维制导律设计［J］.宇航学报，2008，29(6):1798－1803.HAN Dapeng，SUN Weimeng，ZHEN Zhiqiang，et al.A flatness based method for 3D guidance law design［J］.Journal of Astronautics，2008，29(6):1798－1803.(in Chinese)

［12］ 彭双春，孙未蒙，王楠，等.考虑运动耦合的BTT导弹三维制导律设计［J］.航空学报，2010，31(5):968－974.PENG Shuangchun，SUN Weimeng，WANG Nan，et al.3D guidance law of BTT missile considering movement coupling［J］.Acta Aeronautica et Astronautica Sinica，2010，31(5):968－974.(in Chinese)

［13］ 彭双春，潘亮，韩大鹏，等.一种新型三维制导律设计的非线性方法［J］.航空学报，2010，31(10):2018－2025.PENG Shuangchun，PAN Liang，HAN Dapeng，et al.A new 3D guidance law based on nonlinear method［J］.Acta Aeronautica et Astronautica Sinica，2010，31(10):2018 －2025.(in Chinese)

［14］ 彭双春，韩大鹏，潘亮，等.考虑参数优化的BTT导弹三维非线性制导律［J］.控制理论与应用，2011，28(9):1069－1074.PENG Shuangchun，HAN Dapeng，PAN Liang，et al.Threedimensional nonlinear guidance law of BTT missile considering parametric optimization［J］.Control Theory ＆ Applications，2011，28(9):1069－1074.(in Chinese)

［15］ Kane T R，Likins P W，Levinson D A.Spacecraft dynamics［M］.New York，USA:McGraw-Hill Book Company，1983.