多物理场耦合激励下的高铁车内噪声分析
2015-05-16郝志勇马晓龙
毛 杰,郝志勇,孙 强,郑 旭,马晓龙,张 强
(1. 浙江大学能源工程学系,杭州 310027;2. 长春轨道客车股份有限公司,长春 130000)
多物理场耦合激励下的高铁车内噪声分析
毛 杰1,郝志勇1,孙 强2,郑 旭1,马晓龙2,张 强1
(1. 浙江大学能源工程学系,杭州 310027;2. 长春轨道客车股份有限公司,长春 130000)
搭建了整备状态下的某高速列车动力车厢有限元模型,包括白车身、内饰件和牵引传动系统.提出了多物理场激励耦合作用下的高速列车车内结构辐射噪声分析方案,分别采用刚性多体动力学、边界元法和大涡模拟获取了二系悬挂力、轨道噪声和车体表面压力脉动,与车体模态耦合后得到车体结构的振动响应.完成了时速 350,km/h下的列车搭载试验和车体结构响应计算,在地板上随机选取了一个振动测点,仿真与试验得到的振动速度级曲线趋势和幅值具有较高的一致性,验证了仿真模型与多物理场耦合激励的精度.最后采用耦合边界元分析了耦合激励下的车内结构辐射噪声.
高速列车;车内噪声;多物理场耦合激励;耦合边界元
高速列车线路的覆盖面逐渐增广,在给人们出行带来便利的同时也产生了噪声问题.正如沈志云[1]院士所言:“高速列车运行速度限制莫过于噪声,噪声污染超标,一票否决”,他认为列车的低噪声设计是最重要的元素之一.评价高速列车车内噪声的常用方法有 2个,即搭载试验和数值仿真.前者更为有效,可以直接测量不同车速下的噪声,但需要耗费大量的人力和物力,并且可执行机会非常有限.仿真技术的迅速发展很好地填补了这一缺口.
列车在高速行驶过程中,引发车内噪声的核心激励源包括转向架二系悬挂力[2]、轮轨噪声[3]和空气动力噪声[4].
目前,国内外学者对于高速列车车内噪声的仿真分析已有较多的研究.谢素明等[5]创建了某客车白车身的有限元模型并计算了车体结构-车内声腔耦合模态,随后在车体的 4个支点处沿纵向、垂向和横向施加单位简谐力以求解车内噪声;该结果可用于分析机械力与白车身结构噪声之间的传递路径,但对实际车内噪声分析的作用不显著,因为车内噪声的研究对象应是整备车厢,而非白车身.肖友刚等[6]建立了高速列车头车-轨道的耦合动力学仿真模型、车身的有限元模型和边界元模型,计算了由轨道不平顺引起的乘客室内的噪声分布状况和贡献量,但没有考虑轨道噪声、空气动力噪声等主要激励源,因此只能用于分析轨道不平顺激励与车内噪声之间的传递路径.Sapena等[7]采用有限元-统计能量分析混合法搭建了驾驶室的板-梁仿真模型并计算了室内的噪声,将内饰件等效为吸声系数,考虑了机械激励与空气动力噪声激励的耦合作用,但是忽略了轨道不平顺引起的轮轨噪声;此外,虽然考虑了内饰件的吸声性能,但是忽略了它对于结构的约束作用,影响结构响应的精度.
本文在上述学者研究的基础上,考虑了列车高速行驶过程中的较完整的边界条件,采用不同方法提取了转向架二系悬挂力、轮轨噪声和空气动力噪声等来自多个物理场的激励源,最终分析了3种激励耦合作用下的车内振动与声学特性.
1 多物理场耦合声学理论
二系悬挂力通过列车多体动力学获取.在广义坐标系下,基于拉格朗日方程的动力学方程[8]为

式中:ξ为结构的广义坐标,其上“·”和“·”分别表示它对时间的一、二阶导数;M 为结构的质量矩阵,其上“·”表示它对时间的导数;K为广义刚度矩阵;fg为广义质量力;D为模态阻尼矩阵;ψ为约束方程;λ为拉格朗日乘子;Δ为广义坐标系对时间的二阶导数.
轨道不平顺引起的轮轨噪声采用标准的直接边界元算法[9]获取;空气动力噪声通过计算流体动力学与基于Lighthill声类比的FW-H方程[10]获取.
通过上述理论可以提取各个激励源,然后通过耦合间接边界元法计算多物理场耦合作用下的车内振动与声学响应.耦合间接边界元模型由两部分组成:一是与整备车厢有限元模型耦合的边界元 Ωs(具有n1个节点),用于计算车内的结构辐射噪声;二是未与车体耦合的边界元 Ω2(具有 n2个节点),用于提取激励源.已知在 Ω2上法向速度 vn0,则在整个间接边界元上的单层势 σ=0,只需双层势 µ,结构动力学方程[11]为

式中:Ks、Cs和Ms分别为结构的刚度矩阵、阻尼矩阵和质量矩阵;u为结构位移向量;Fs为作用在结构上的外载荷(不包括声压载荷);Lcµ为声压作用在结构上的载荷;Lc为耦合矩阵.
2 整备车厢有限元建模
整备车厢的有限元模型主要包括白车身、内饰件和牵引传动系统.各个结构的材料属性与实车基本一致,提升计算模型的精度.
我国运营的高速列车白车身均采用大型中空铝合金挤压型材组焊成筒型整体承载结构,不同区域的铝合金型号略有差异,但材料的密度、弹性模量和泊松比基本相同,分别取值为 2,685,kg/m3、72.4,GPa和0.3.白车身有限元模型及其截面结构如图1所示,由457,442个四边形单元组成.

图1 白车身有限元模型Fig.1 Finite element model of body-in-white
内饰件从下而上主要包括沥水板、隔热吸声层、地板系统(由胶黏剂、木骨、减振垫、地板和地板布组成)、座椅、门窗、木质间壁(洗手间、电气柜等)、玻璃间壁、侧墙板、行李架和通风系统(车顶通风板和空调系统).在所有内饰件中,对车体振动与声学响应有影响的结构均需要体现在整备车厢有限元模型中,其他可以省略或者等效为附加质量,如图 2(a)所示,由381,674个六面体单元和四边形单元组成.
在汽车、飞机等其他交通工具的内部声场研究中,一般都省略内饰件并将其等效为吸声系数.对于结构的振动或声学响应而言,这种研究思路并不是理想的处理方法.对于以较大刚度附着在白车身上的内饰件,如列车地板,对车体有很大约束,因此需要在建模过程中予以考虑.
牵引传动系统的有限元模型重点考虑了转向架,并将车下电气设备简化为均布质量施加在白车身模型对应的节点上.本文研究的动力车厢不带受电弓,但装配动力转向架,如图2(b)所示.动力转向架的主要零部件包括车身连接架、构架、牵引电机、轮对、轴箱、一系悬挂、二系悬挂和减振系统等.

图2 整备车厢有限元模型Fig.2 Finite element model of the curb coach
3 多物理场边界条件提取
3.1 二系悬挂力
在轮轨表面粗糙度的作用下,车轮与轨道之间会产生较大的作用力,不仅激发轮轨产生噪声,还经转向架悬挂系统的衰减传递到二系空气弹簧悬挂上,最终以二系悬挂力的形式作用在转向架忱梁上,激发车体结构振动并辐射噪声.
如上文所述,二系悬挂力的提取基于刚性多体动力学,计算模型和所需的刚体参数分别如图3和表1所示(其他减振器的阻尼在模型中均有体现,文中不再赘述).
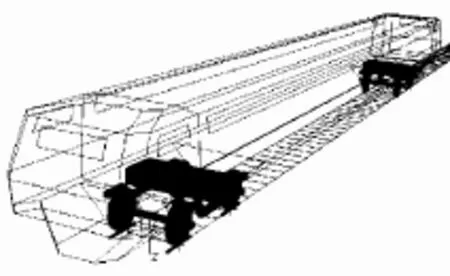
图3 车厢刚性多体动力学模型Fig.3 Rigid multi-body dynamic model of the coach

表1 车厢刚体参数Tab.1 Rigid-body parameters of the carriage
在标准轨道谱的激励下,经转向架悬挂系统的衰减,得到时速 350,km/h下 0~200,Hz频段内的垂向二系悬挂力(选取前转向架右二系悬挂为例),如图 4所示.在分析频域内,二系悬挂力主要集中在 25~75,Hz,峰值接近5,kN;在75~175,Hz内幅值也有一定的起伏.由于列车是匀速直线行驶,因此沿着轨道和侧向的力不在文中考虑.

图4 转向架垂向二系悬挂力Fig.4 Normal secondary suspension forces of the bogies
3.2 轨道噪声
轨道噪声包括滚动噪声、冲击噪声和曲线啸叫声,是列车高速行驶时主要噪声源之一[12].在数值分析时,研究并控制轨道噪声的首要任务是建立合理且有效的预测模型.本次研究的搭载试验在京沪高铁线路上完成,参考该线路板式轨道结构并建立有限元模型,包括钢轨、扣件、轨道板和混凝土底座,如图5所示.底座下方的基础梁体在后续计算模型中用接地弹簧等效处理.固定钢轨的扣件通常由弹条、预埋铁座、绝缘轨距块和橡胶垫板,需要具有足够的强度、耐久性及一定的弹性.在建模过程中,为了体现扣件的机械性能,将其简化为一组弹簧-阻尼单元.

图5 板式轨道有限元模型Fig.5 Finite element model of the slab track
轨道的结构辐射噪声由车轮与钢轨作用产生的轮轨力激发.轮轨力通过上述的多体动力学获取,选取前转向架前轮对与轨道在 350,km/h下的垂向轮轨力为例,其频域结果如图 6所示.每一个轮对左右侧的轮轨力频域曲线基本一致,并在10,Hz附近出现了较大的幅值(超过 5,kN),可能是刚性体与标准轨道谱之间产生共振有关.

图6 某轮对垂向轮轨作用力Fig.6 Wheel-rail interaction induced force of a wheel set in the vertical direction
轮轨力作用下的轨道辐射噪声声功率级如图 7所示.在 50,Hz附近,引起轨道噪声较大的原因主要有两个:一是轮轨力在 50,Hz时有较大的峰值,二是轨道结构在50,Hz下具有整体模态,因此在两者的耦合下,轨道辐射出较大的噪声.

图7 轨道结构辐射噪声声功率级Fig.7 Acoustic power level of railway structure-borne noise
3.3 空气动力噪声
当车速超过 300,km/h后,空气动力噪声将成为列车的另一个主要噪声源[13],因此需要考虑车外流场激励下的车内噪声,即风噪.高速列车气动噪声主要产生于列车的凹凸表面,如受电弓、转向架等结构附近.目前暂时无法直接模拟气动噪声源及其传播,尤其对于列车这类超大模型.本文采用大涡模拟(large-eddy simulation,LES)计算流场作用在车体表面的压力脉动,再结合流固耦合技术[14]分析压力脉动与车体模态的耦合效应,最终计算车外流场作用下的振动响应及风噪.
为了获取压力脉动,搭建了列车的风洞模型,包括风洞轮廓、进风口、头车、被研究车、尾车和出风口,如图 8所示,其中头车和尾车的主要作用是保证被研究车表面有顺畅的流场,与实际情况相仿.风洞尺寸和大涡模拟参数如表2所示.在保证0~200,Hz频段内的表面压力脉动精度的前提下,为了大幅缩减计算周期,建模时将被研究车表面的单元画得较细,头车和尾车表面的单元画得较粗;车体表面向风洞轮廓过渡的空气流场单元呈由密至疏分布.

图8 用于大涡模拟的列车风洞模型Fig.8 Wind tunnel model of the train for large-eddy simulation
计算完成后,选取 50,Hz和 100,Hz下的车体表面脉动压力级为例,如图 9所示.车体表面的压力脉动主要集中在风挡和转向架区域,因为这些区域表面结构不流畅,迎风经过时会受到较大的阻碍,形成了紊流,使得流场与车体表面的作用加剧,产生明显的压力脉动.在其他区域,车体表面压力脉动小而均匀,流场以层流为主.
车外流场在车体表面形成的压力脉动与车体模态发生耦合,进而引起车体结构响应,最终向车内辐射噪声,形成风噪.

表2 风洞模型尺寸和大涡模拟参数Tab.2 Dimension of the wind tunnel model and the parameters of LES

图9 车体表面脉动压力级云图Fig.9 Fluctuating pressure level contour from thecoach surface
4 多物理场耦合下的车内噪声分析
列车仿真模型在结构上是理想的,即没有任何的漏声、异响等,同时也忽略空调、变电系统、设备冷却装置等运行时的噪声.因此,仿真获取的车内噪声是上述3种激励与车体模态耦合后引发车体结构振动,进而向车厢内部辐射的结构噪声.这样,车内噪声的仿真与试验结果很难对比分析,因为试验过程中,车内声场包含了结构辐射噪声,但除此之外会受到试验人员、会车、建筑物、隧道等无法避免的干扰因素.
由于结构辐射噪声来自于结构表面的振动,因此,为了保证多物理耦合下的车内结构辐射噪声仿真精度,选取车内结构的振动响应作为验证参数.在列车搭载试验时,随机选择车厢内地板上的一个测点作为观测点,其位置如图 10(a)所示,采用振动速度级评价测点的结构响应,即

式中:Lv为振动速度级;v为机体表面的振动速度;v0为参考速度,5×10-8,m/s.
图10(b)所示为仿真与试验振动速度级对比. 从图 10(b)中可以看到,仿真与试验振动速度级曲线具有较高的一致性,仿真结果基本上捕捉到了试验的大多数峰值,但在个别频率下形成了一定的误差.总体而言,由于列车的结构和受到的激励均十分复杂,但是本文已考虑了引起车内噪声的主要激励源.对于如此复杂的工程问题,该结果较为理想.

图10 观测点位置及仿真与试验振动速度级对比Fig.10 Location of the measuring point and the comparison of the simulated and measured vibration velocity levels
列车车内的声学响应通过耦合边界元法获取,将上述3种激励作为声学计算的边界条件,与整车车厢的模态发生耦合,得到二系悬挂力、轨道噪声和空气动力噪声耦合作用下的车内中心、距离地板1.2,m处的结构辐射噪声,如图 11所示.在分析频域内,车内噪声总体上呈现上升的趋势,并在 100,Hz附近明显出现了低谷.

图11 多物理场激励耦合下的车内中心噪声声压级Fig.11 SPL at the coach interior center under the multiphysical-field coupled excitations
本文暂未考虑车内声学包装的吸声性能,因为它需要基于吸声试验确定,而不能采用一个经验值,这会影响计算精度.由于目前课题组尚无法获取完整的声学包装试件,故图 11中的声学结果仅仅是车体结构振动引起的辐射噪声,声能未经声学包装吸收,也未受到漏声、试验人员的影响,是多物理场耦合激励作用下的“原始”噪声.由于结构的振动响应仿真结果得到了搭载试验的验证,故上述声学结果是较为准确的车体结构辐射噪声.在后续研究中,可以对该声学结果实施优化.
5 结 论
(1) 搭建了整备状态下的某高速列车动力车厢有限元模型,可以提升车体结构响应的精度.
(2) 基于多体动力学、边界元法和大涡模拟分别提取了 350,km/h下的二系悬挂力、轨道噪声和车体表面压力脉动等来自不同物理场的激励.
(3) 完成了列车搭建试验和多物理场耦合激励作用下的车体结构响应计算,随机在地板上选取了一个振动测点,仿真与试验得到的振动速度级曲线具有较高一致性,可保证仿真模型及振动响应的精度.
(4) 计算了多物理场耦合激励作用下的车内结构辐射噪声,可结合后续优化工作降低车体结构振动引起的声学响应.
[1] 沈志云. 高速列车的动态环境及其技术的根本特点[J]. 铁道学报,2006,28(4):1-5.
Shen Zhiyun. Dynamic environment of high-speed train and its distinguished technology[J]. Journal of the China Railway Society,2006,28(4):1-5(in Chinese).
[2] 宫 岛,周劲松,孙文静,等. 高速列车弹性车体与转向架耦合振动分析[J]. 交通运输工程学报,2011,11(4):41-47.
Gong Dao,Zhou Jinsong,Sun Wenjing,et al. Coupled vibration analysis of flexible car body and bogie for high-speed train[J]. Journal of Traffic and Transportation Engineering,2011,11(4):41-47(in Chinese).
[3] Jones C J,Thompson D J,Diehl R J. The use of decay rates to analyse the performance of railway track in rolling noise generation[J]. Journal of Sound and Vibration,2006,293(3/4/5):485-495.
[4] Mellet C,Letourneaux F,Poisson F,et al. High speed train noise emission:Latest investigation of the aerodynamic/rolling noise contribution[J]. Journal of Sound and Vibration,2006,293(3/4/5):525-546.
[5] 谢素明,付亚兰,王悦东,等. 铁路客车结构-声耦合系统的声学特性[J]. 大连交通大学学报,2008, 29(5):40-44.
Xie Suming,Fu Yalan,Wang Yuedong,et al. Acoustic property of structure-acoustic coupling system for rail car [J]. Journal of Dalian Jiaotong University,2008,29(5):40-44(in Chinese).
[6] 肖友刚,康志成. 高速列车乘客室内轮轨激励噪声的贡献度分析[J]. 华南理工大学学报:自然科学版,2009,37(2):98-101,106.
Xiao Yougang,Kang Zhicheng. Acoustic contribution analysis of passenger room of high-speed train under wheel-rail excitation[J]. Journal of South China University of Technology:Natural Science Edition,2009,37(2):98-101,106(in Chinese).
[7] Sapena J,Tabbal A,Jove J,et al. Interior noise prediction in high-speed rolling stock driver’s cab:Focus on structure-borne paths(mechanical and aero sources) [J]. Noise and Vibration Mitigation for Rail Transportation Systems,2012,118(1):445-452.
[8] Mao Jie,Hao Zhiyong,Jing Guoxi,et al. Sound quality improvement for a four-cylinder diesel engine by the block structure optimization[J]. Applied Acoustics,2013,74(1):150-159.
[9] Brancati A,Aliabadi M H. Boundary element simulations for local active noise control using an extended volume[J]. Engineering Analysis with Boundary Elements,2012,36(2):190-202.
[10] Tadamasa A,Zangeneh M. Numerical prediction of wind turbine noise[J]. Renewable Energy,2011,36 (7):1902-1912.
[11] Paiva B J,Mendonca A V. A coupled boundary element/differential equation method formulation for platebeam interaction analysis[J]. Engineering Analysis with Boundary Elements,2010,34(5):456-462.
[12] Pieringer A,Kropp W,Thompson D J. Investigation of the dynamic contact filter effect in vertical wheel/rail interaction using a 2D and a 3D non-Hertzian contact model[J]. Wear,2011,271(1/2):328-338.
[13] Raghunathan R S,Kim H D,Setoguchi T. Aerodynamics of high-speed railway train[J]. Progress in Aerospace Sciences,2002,38(6/7):469-514.
[14] Hou G,Wang J,Layton A. Numerical methods for fluidstructure interaction:A review[J]. Communications in Computational Physics,2012,12(2):337-377.
(责任编辑:金顺爱)
High-Speed Train Interior Noise Analysis Under Multi-Physical-Field Coupled Excitations
Mao Jie1,Hao Zhiyong1,Sun Qiang2,Zheng Xu1,Ma Xiaolong2,Zhang Qiang1
(1. Department of Energy Engineering,Zhejiang University,Hangzhou 310027,China;2. Changchun Railway Vehicles Company Limited,Changchun 130000,China)
A finite element model of a curb high-speed-train motored coach was constructed,including its body-inwhite,interior trim parts and traction system. An analytical scheme on the interior structural radiated noise of a highspeed train under multi-physical-field coupled excitations was proposed. Rigid multi-body dynamics,boundary element method and large-eddy simulation were employed to extract secondary suspension forces,railway noise and surface pressure fluctuations,respectively. The excitations were coupled with the coach modes to obtain the structural vibration response. The on-line test and structural response simulation of the coach were conducted at 350,km/h. A measuring point of vibration was randomly selected on the floor. The tendency and amplitude of the vibration velocity level curves from the test and simulation agreed well with each other,which validated the precisions of the numerical model and the multi-physical coupled excitations. Finally,coupled boundary element method was adopted to analyze the interior structural radiated noise under the coupled excitations.
high-speed train;interior noise;multi-physical-field coupled excitation;coupled boundary element
TB532
A
0493-2137(2015)03-0240-06
10.11784/tdxbz201310015
2013-10-19;
2013-12-02.
国家高技术研究发展计划(863计划)资助项目(2011AA11A103).
毛 杰(1987— ),男,博士研究生,maojie1987@zju.edu.cn.
郝志勇,haozy@zju.edu.cn.
时间:2014-02-28.
http://www.cnki.net/kcms/detail/12.1127.N.20140228.1315.006.html.
