基于变频率区间约束的结构材料优化设计

赵志军，荣见华，黄方林，俞燎宏

(1.中南大学土木工程学院，长沙 410000;2.长沙理工大学汽车与机械工程学院，长沙 410076; 3.长沙学院土木工程系，长沙 410003)

基于变频率区间约束的结构材料优化设计

赵志军1，3，荣见华2，黄方林1，俞燎宏2

(1.中南大学土木工程学院，长沙 410000;2.长沙理工大学汽车与机械工程学院，长沙 410076; 3.长沙学院土木工程系，长沙 410003)

针对频率约束的结构材料优化问题，基于结构拓扑优化思想，提出变频率区间约束的结构材料优化方法。借鉴均匀化及ICM(独立、连续、映射)方法，以微观单元拓扑变量倒数为设计变量，导出宏观单元等效质量矩阵及导数，进而获得频率一阶近似展开式。结合变频率区间约束思想，获得以结构质量为目标函数、频率为约束条件的连续体微结构拓扑优化近似模型;采用对偶方法求解。通过算例验证该方法的有效性及可行性，表明考虑质量矩阵变化影响所得优化结果更合理。

微结构;拓扑优化;频率约束;材料设计

对有序多孔材料静态弹性行为及动力学分析研究，由性能分析到实验制备等获得大量成果［1－2］。由于有序多孔材料构成的复杂大型结构离散完全计算量巨大，等效连续介质分析方法研究取得较大进展。其中，代表体单元法(Representative Volume Element，RVE)及数学均匀化方法为两种求解周期性多孔材料等效材料特性的代表性方法。基于小参数展开理论的均匀化方法具有较严格的数学基础，广泛用于复合材料弹性常数预测。均匀化理论将周期性多孔材料结构力学分析问题分解为微结构与宏观结构问题，并通过微结构的等效材料特性及特征位移(称影响函数)实现两尺度有限元分析耦合。Xing等［1］提出周期性复合材料的高效近似分析方法，如特征单元(eigenelement)法与基于高阶单元的serendipity特征单元法等。Sigmund［3］提出的复合材料微结构单胞拓扑优化设计理论，已跻身材料研究领域前沿。Hassani等［4－5］对均匀化理论进行过系统阐述。Niu等［6］采用均匀化方法进行结构最大自然频率两种尺度拓扑优化设计。Huang等［7］基于渐进结构优化方法(Evolutionary StructuralOptimization，ESO)进行最大刚度的结构材料设计。Zuo等［8］采用渐进优化方法实现结构最大自然频率的多尺度拓扑优化设计。然而，该方法忽略了结构质矩阵变化影响。尽管已开展基于拓扑优化的材料设计，但涉及结构频率要求的材料设计较有限。

本文借鉴均匀化方法及ICM(独立、连续、映射)方法，以微观单元拓扑变量倒数为设计变量，从有限元基本理论出发，推导出宏观单元等效质量矩阵及导数，结合等效弹性模量显示表达［4－5］，获得频率的一阶近似显式展开式。结合变频率区间约束思想，获得以结构质量为目标函数、频率为约束条件的连续体微结构(即材料)拓扑优化近似模型，并采用对偶方法进行求解。利用两算例验证本文方法的有效性与可行性。

1 微观尺度下单元拓扑变量与过滤函数

设宏观结构由周期性多孔材料组成。基于代表体单元法及数学均匀化方法思想，宏观结构由宏观单元构成，而宏观单元作为微观结构(即材料)由微观单元构成。设第s号微观单元的拓扑变量为t。用过滤函数fD(t)识别第s号微观单元弹性矩阵、fm(t)识别第s号微观单元密度。单元材料特性参数识别式为

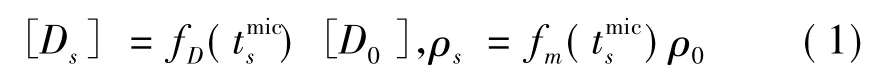
式中:［D0］为微观单元固有弹性模量矩阵;ρ0为微观单元固有材料密度;［Ds］为识别后弹性模量矩阵;ρs为识别后材料密度。

密度及弹性模量矩阵的过滤函数分别采用分式有理式与幂指数函数形式，即

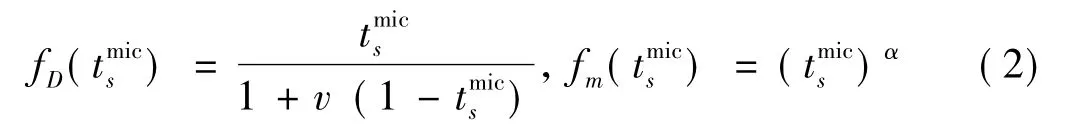
本文算例中取v=3.5，α=1.0。

2 微观尺度下频率近似显式表示式

2.1 宏观结构总刚度阵对微观单元设计变量导数

宏观尺度下，第i号宏观单元刚度矩阵［2－3］可表示为

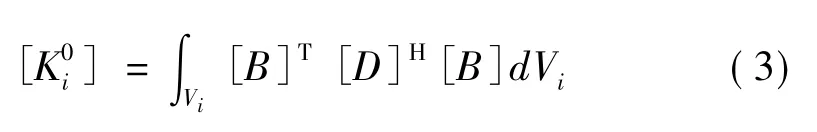
式中:Vi为第i号宏观单元体积;[B]为宏观单元应变矩阵;［D］H为宏观单元等效弹性模量矩阵［4－5］，表示式为

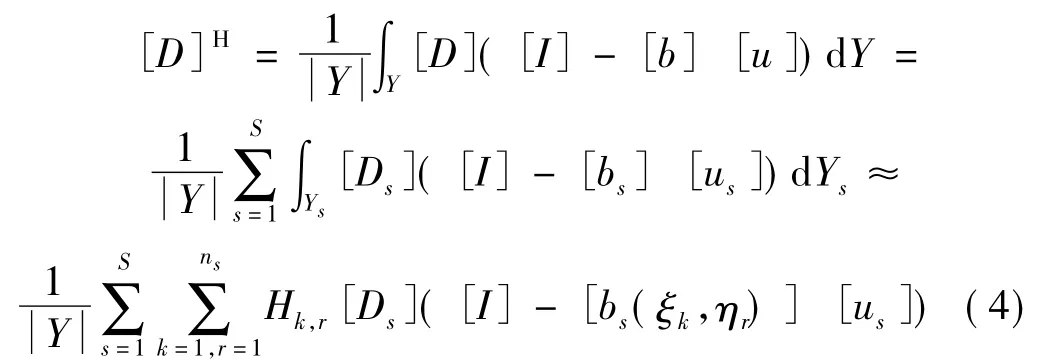
式中:［D］H为宏观结构等效弹性模量矩阵;Y为单胞(宏观单元)体积(对均匀划分的结构单元网格，Y= Vi);［D］为微观结构基材料的弹性模量矩阵;［b］为微观结构基材料应变矩阵;［u］为初应变场引起的位移场;S为单胞内微观单元个数;［us］为第s个微观单元节点位移向量;［bs(ξk，ηr)］为第s个微观单元高斯积分点(ξk，ηr)(对二维问题)处应变矩阵;Hk，r为积分权系数;ns为高斯积分点个数，本文ns=2;Ys为第s个微观单元体积。

为求解［u］，需在微观单元结构上施加初应变场，其等效节点荷载计算式为

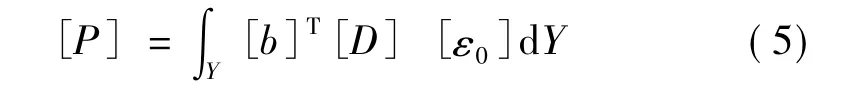
式中:［P］为初应变场等效节点荷载;［ε0］为应变场，对平面应力问题，{1，0，0}T，{0，1，0}T，{0，0，1}T为［ε0］的列向量。

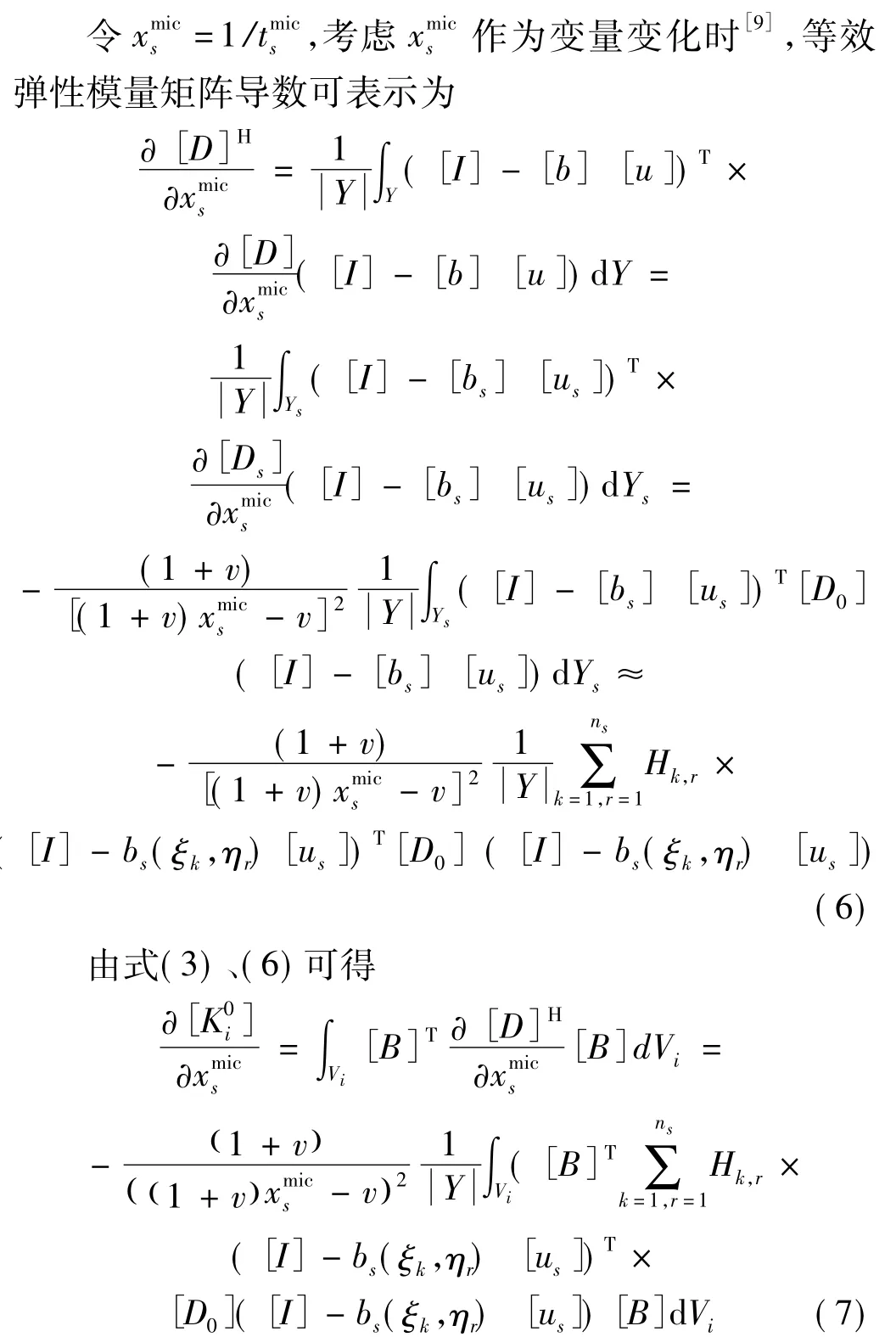
类似，式(7)可表示成第i号宏观单元的高斯积分求和形式。宏观整体刚度矩阵对微观单元设计变量的导数可表示为

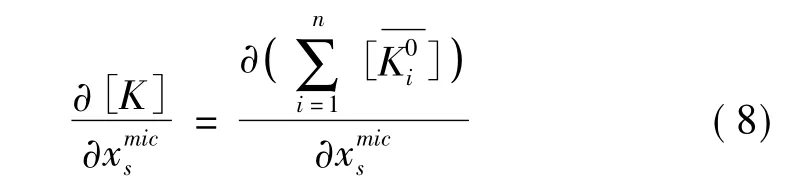
2.2 宏观结构整体质量阵对微观单元设计变量导数

宏观单元任意点单位体积的惯性力可表示为

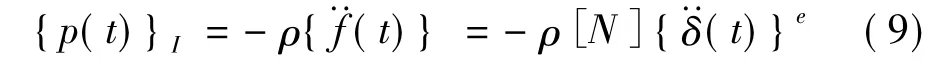
宏观单元惯性力形成的节点力向量可表示为

式中:Vi为第i号宏观单元体积。

宏观尺度下，第i号宏观单元等效质量矩阵可表示为

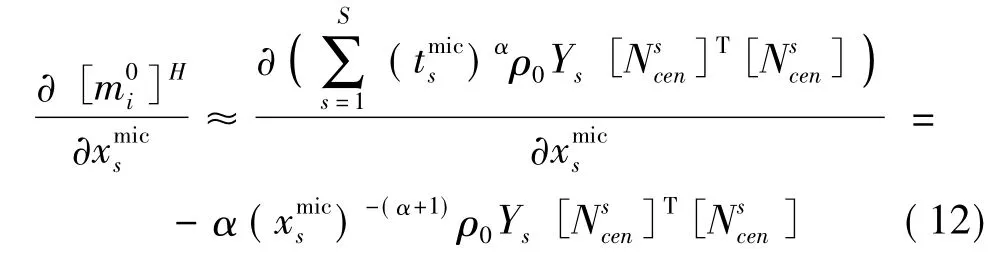
宏观整体质量矩阵对微观单元设计变量的导数可表示为

2.3 频率一阶近似展开式

结构频率对微观设计变量的导数为

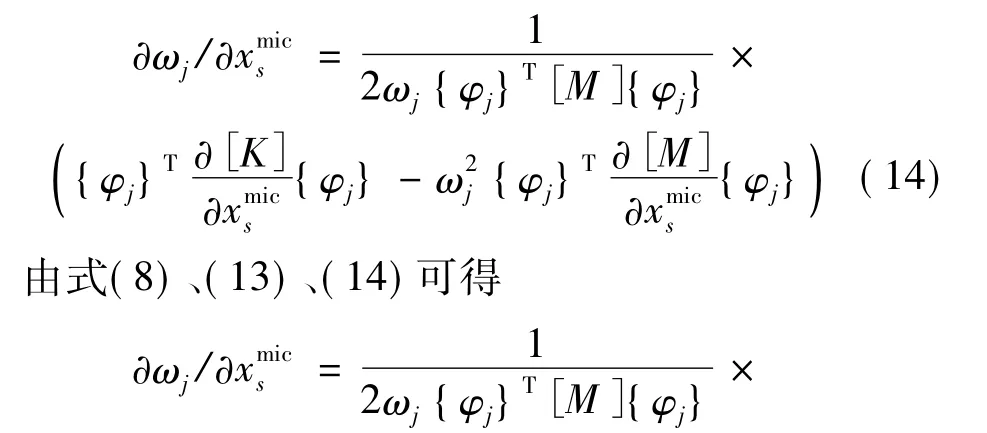
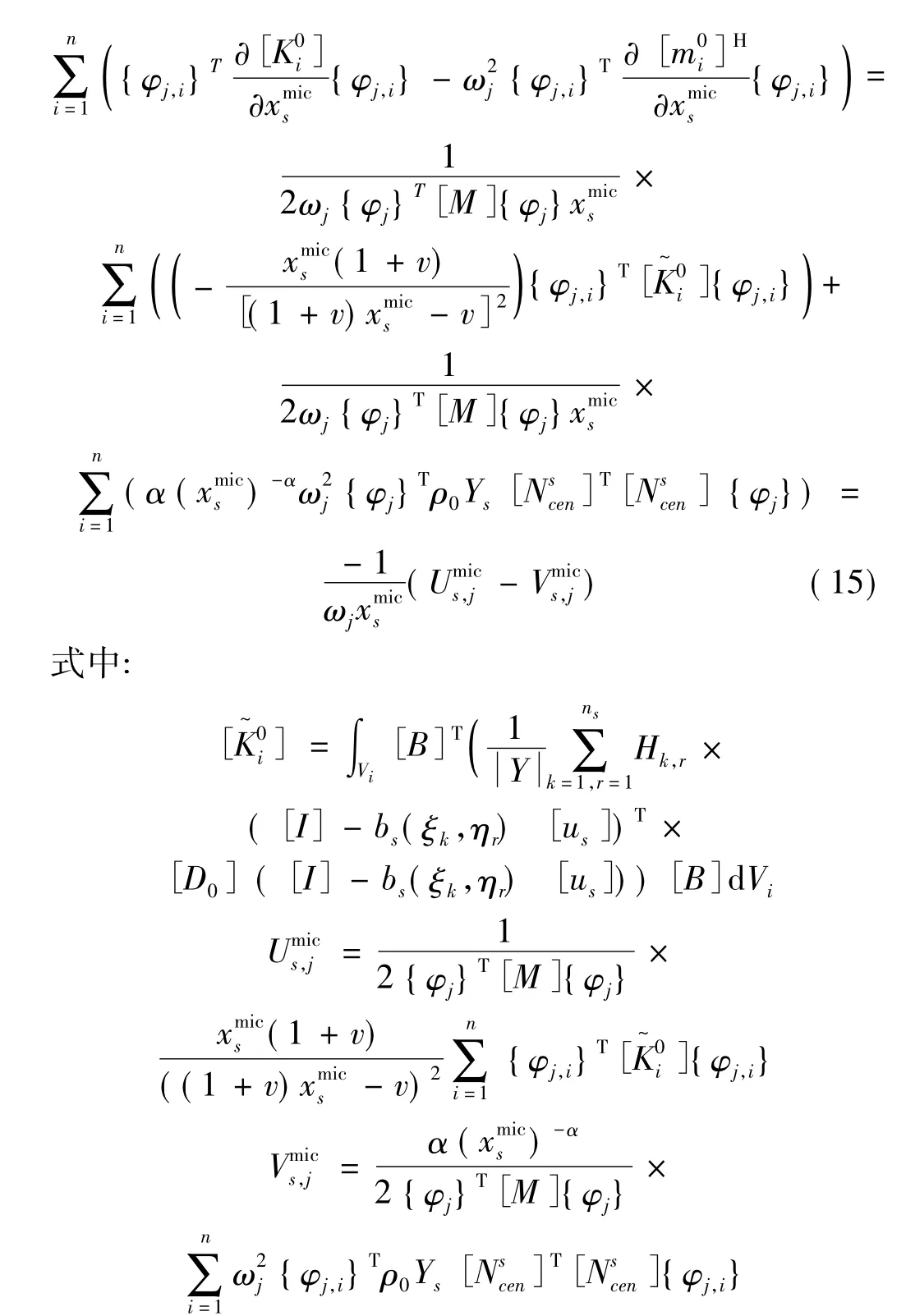
式中:{φj，i}为第j阶振型向量与第i号单元相关部分。进而可得频率一阶近似展开式为

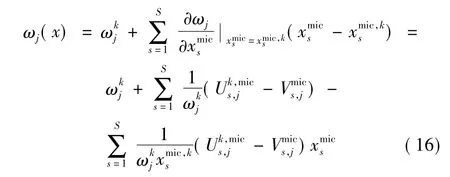
3 变频率区间约束优化模型处理及求解方法

设结构宏观单元个数为N，每个宏观单元划分为S个微观单元，其单元编号可设为s(s=1，2，…，S)。其中J为频率约束阶数;t为第s个拓扑变量;为其下限;w为第i个宏观单元第s个单元固有重量。优化求解模型为

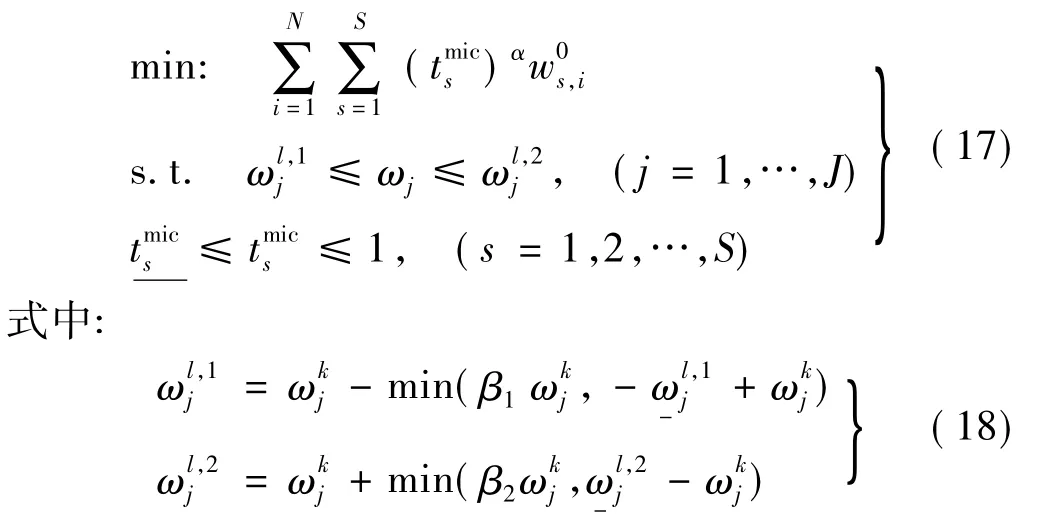
式中:β1，β2为频率约束限变化因子，可在0.02～0.08间取值。变频率区间限ω，ω在一轮优化迭代中不变，在下一轮优化迭代中ω，ω按式(18)变化，为频率约束的下、上限值。

由于频率与质量矩阵、刚度矩阵的关联性，优化求解过程中频率变化趋势具有双方向性特点。本文采用式(18)变区间约束方式将每一迭代步频率变化控制在一定范围内，该方式既能较好模拟频率变化的双方性特点，又能保证一阶近似展开式成立，可有效避免目标函数振荡现象。

式(17)的求解可转化为

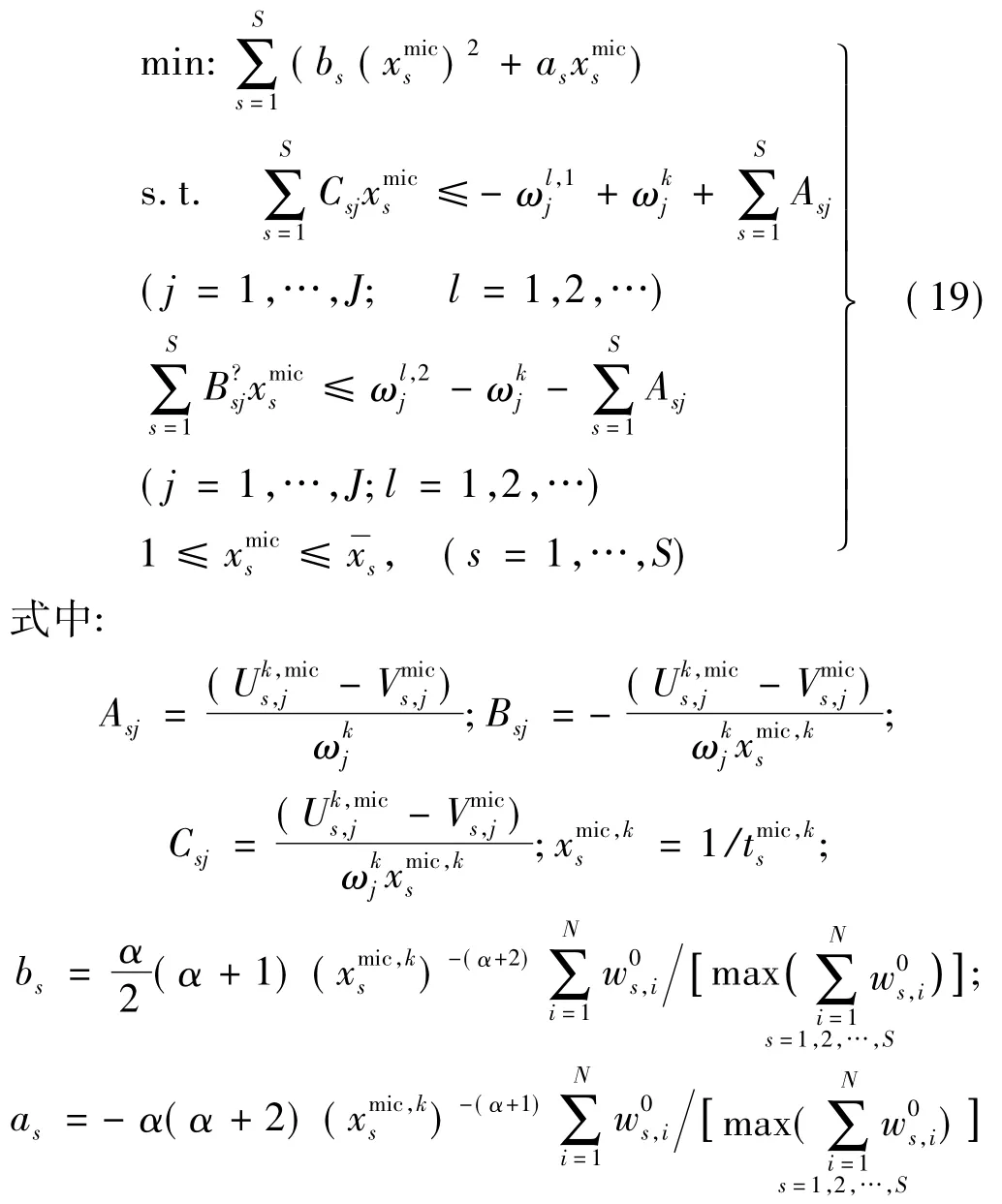
为处理优化结构的棋盘格问题，采用类似于文献［10］方法，对式(19)中所有非人工材料单元对应的Asj，Bsj，Csj，as，bs进行修正;将修正后Asj，Bsj，Csj，as，bs代入式(15)。采用对偶理论将模型(19)的规划问题转化为对偶规划问题求解，即

取φ(λ)的二阶近似并略去常数项，获得二次规划模型为

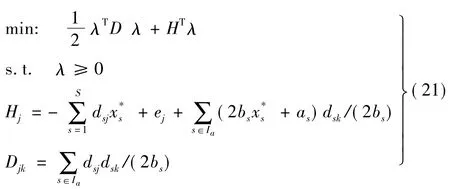
解此二次规划，求出λ，再由K－T条件求出x*、由x=1/ts求出t*，对结构进行修改，通过式(18)近似算出约束频率限，获得式(19)的各系数，重复求解λ及t*直至‖xs+1－xs‖/‖xs‖≤ε3(s为本轮循环迭代次数，ε3为初始给定小量)终止本轮循环迭代，并将该迭代解用t(k+1)表示。

4 优化求解程序设计

针对微观结构优化问题，优化设计流程见图1。

图1 优化设计流程图Fig.1 Flow chart of the optimization design

5 算例

5.1 算例一

图2(a)为80 m×40 m平面应力梁，两端固支，厚度1 m，弹性模量E=1 Pa，泊松比υ=0.3，密度ρ=1.0 kg/m3。宏观设计区域划分为80×40有限元网格，将单胞划分为40×40有限元网格，见图2(b)。

以宏观结构重量为目标函数、第一阶自振频率为约束条件，约束限值取=0.01 rad/s，=0.02rad/s。宏观尺度80 m×40 m两端固定梁微观结构优化进化历程见图3，重量进化历程见图4，基频进化历程见图5。本文优化结果与文献［8］优化结果对比见图6。本文第33迭代步所得结构重量及频率较接近文献［8］结果，但结构最优拓扑有所区别，体现出考虑质量矩阵对设计变量导数项所致优化结果的不同。因此忽略质量矩阵一阶量会产生误差。

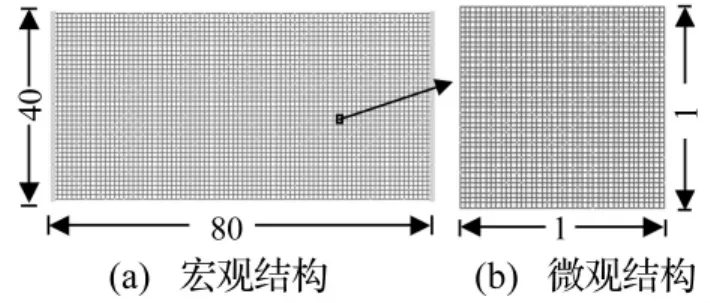
图2 初始设计区域Fig.2 Initial design domain

图3 宏观尺度为80×40微观结构进化历程Fig.3 The optimization history of micro structure of the 80×40 double－clamped beam

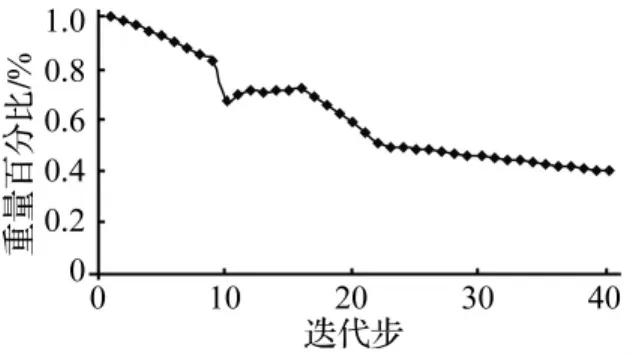
图4 结构重量进化历程Fig.4 History of weight fraction

图5 结构基频进化历程Fig.5 History of fundamental frequency

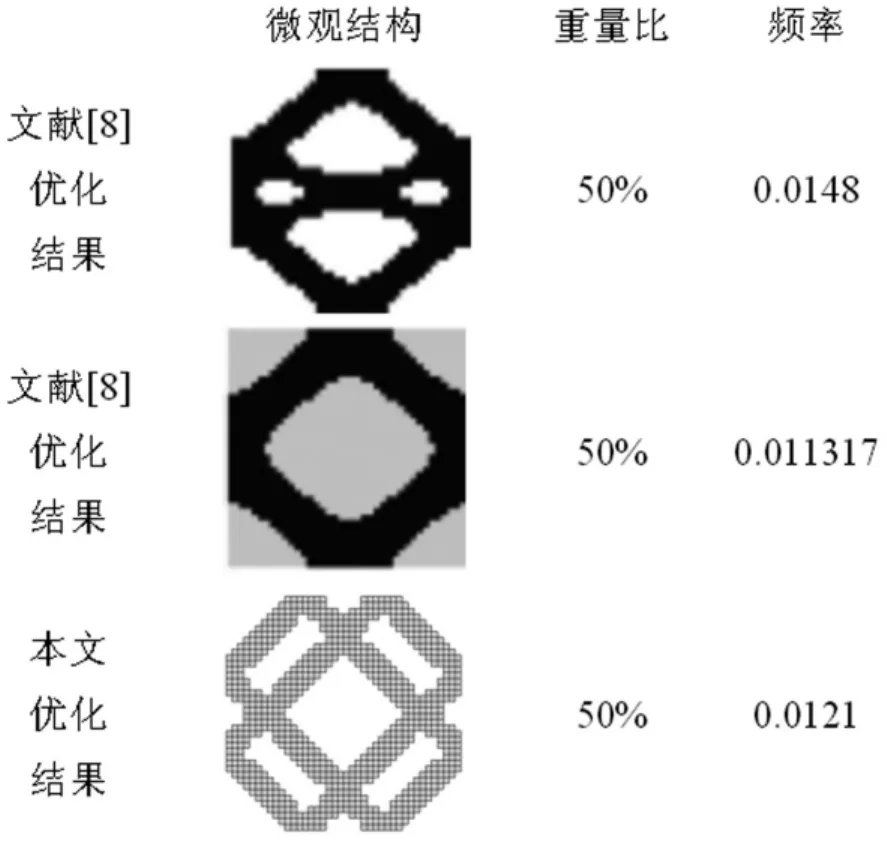
图6 采用不同优化方法所获得优化结果的对比Fig.6 Comparison on different designs by using different optimization method

5.2 算例二

图7(a)为60 m×60 m平面应力梁，两端固支，厚度1 m。设弹性模量E=1 Pa，泊松比υ=0.3，密度ρ= 1.0 kg/m3。宏观设计区域划分为60×60有限元网格，将微观单胞划为40×40有限元网格，见图7(b)。以结构总重量为目标函数、第一阶自振频率为约束条件，约束限值取=0.02 rad/s，=0.03 rad/s，宏观尺度为60 m×60 m两端固定梁微观结构优化进化历程见图8，重量进化历程见图9，基频进化历程见图10。

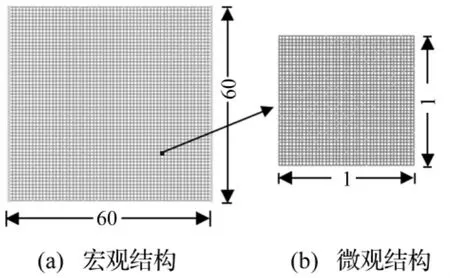
图7 初始设计区域Fig.7 Initial design domain

图8 宏观尺度为60×60微观结构进化历程Fig.8 The optimization history of micro structure of the 60×60 double－clamped beam

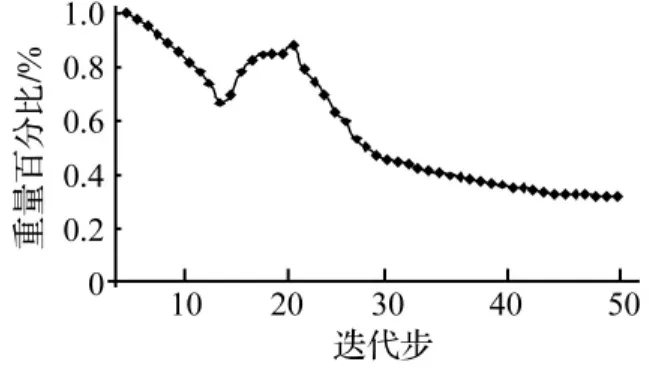
图9 结构重量进化历程Fig.9 History of weight fraction

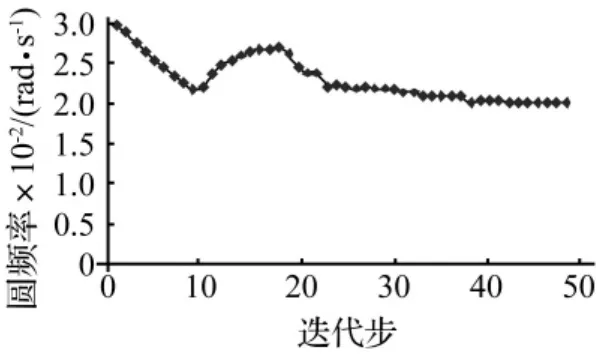
图10 结构基频进化历程Fig.10 History of fundamental frequency

6 结论

针对频率约束拓扑优化问题，提出变频率区间约束的连续体微观结构拓扑优化方法，并给出两算例。结论如下:

(1)所提方法能有效优化设计考虑频率约束的连续体微观结构。

(2)在频率近似式中，考虑宏观单元等效质量矩阵的一阶量影响，可使优化近似模型更有效，更能避免目标函数振荡现象发生。

［1］Xing Y F，Yang Y.An eigenelement method of periodical composite structures［J］.Composite Structures，2011，93(2): 502－512.

［2］Neto M A，Yu W B，Tang T，et al.Analysis and optimization of heterogeneous materials using the variational asymptoticmethodforunitcellhomogenization［J］. Composite Structures，2010，92(12):2946－2954.

［3］SigmundO.Materialswithprescribedconstitutive parameters:aninversehomogenizationprobiem［J］. Internationai Journai of soiids and Structures，1994，31(17): 2313－2329.

［4］Hassani B，Hinton E.A review of homogenization and topology optimization I－homogenization theory for media with periodic structure［J］.Comput Struct，1998，69(6):707－717.

［5］Hassani B，Hinton E.A review of homogenization and topology optimization II－analytical and numerical solution of homogenization equations［J］.Comput Struct，1998，69(6): 719－738.

［6］Niu B，Yan J，Cheng G.Optimum structure with homogeneous optimum cellular material for maximum fundamental frequency［J］.Struct Multidisc Optim，2009，39(2):115－132.

［7］Huang X，Zhou S W，Xie Y M，et al.Topology optimization of microstructures of cellular materials and composites for macrostructures［J］.Computational Materials Science，2013，67:397－407.

［8］Zuo Zhi－hao，Huang Xiao－dong，Rong Jian－hua，et al.Multiscale designofcompositematerialsandstructuresfor maximum natural frequencies［J］.Materials and Design，2013，51:1023－1034.

［9］Yi Y M，Park S H，Youn S K.Design of microstructures of viscoelastic composites for optimal damping characteristics［J］.International Journal of Solids and Structures，2000，37(35):4791－4810.

［10］邢晓娟，荣见华，邓果.一种变频率约束限的结构拓扑优化方法［J］.振动与冲击，2008，27(10):56－60.

XING Xiao－juan，RONG Jian－hua，DENG Guo.A structural topologic optimization method based on varying frequency constraint limits［J］.Journal of Vibration and Shock，2008，27(10):56－60.

Topology optimization of micro structures with varying frequency interval constraints

ZHAO Zhi－jun1，3，RONG Jian－hua2，HUANG Fang－lin1，YU Liao－hong2
(1.School of Civil Engineering，Central South University，Changsha 410000，China; 2.School of Automotive and Mechanical Engineering，Changsha University of Science and Technology，Changsha 410076，China; 3.Department of Civil Engineering，Changsha University，Changsha 410003，China)

Based on the idea of structural topology optimization，a structural material optimization method considering varying frequency interval constraints was proposed.By use of homogenization and ICM(Independence，Continuity and Mapping)method，the effective mass matrix and its derivatives were established by taking the reciprocal topological variables of micro structural elements as design variables，and the first order approximate explicit functions of frequency interval constraints were constructed.Integrating with the idea of varying frequency interval constraints，a topological optimization model of micro structures was formed by taking the structural mass as objective function and the frequency as constraint function.Here，a dual solving method was adopted.The results of two examples show that the proposed method is feasible and effective，and the optimal result obtained by the proposed method，where the variation of mass matrix is considered，is more reasonable.

micro structure;topology optimization;frequency constraint;material design

TU311.3;TB123

A

10.13465/j.cnki.jvs.2015.02.018

国家自然科学基金项目(11372055，51228801);长沙理工大学桥梁工程湖南省普通高校重点实验室开放基金(10KA07);长沙学院科研基金项目(CDJJ－10010110)

2013－11－08修改稿收到日期:2014－01－28

赵志军男，博士生，讲师，1982年2月生

荣见华男，博士，教授，1963年7月生

邮箱:rongjhua@yahoo.com.cn