三对角线型行列式的求法

李海英，赵建英

（内蒙古商贸职业学院社科基础部，呼和浩特 010022）

三对角线型行列式的求法

李海英，赵建英

（内蒙古商贸职业学院社科基础部，呼和浩特 010022）

三对角线型行列式是线性代数中一种常见的具有特殊格式的行列式，通过举例的方式对此类行列式的计算进行探讨，由简单形式的行列式到元素复杂的行列式进行推导，并在行列式的元素满足一定条件的情形下，得到一般形式三对角线型行列式的计算方法及其计算公式。

三对角线型行列式；递推公式；消去法

三对角线型行列式[1]是n阶行列式中一种常见的行列式，此行列式的特点是，除主对角线及其上下两条次对角线的元素外，其余的元素都为零。对于此类行列式，我们需要寻找其所具有的具体特点，进而确定具体的计算方法，得到一般的计算公式。下面我们通过举例的方式对三对角线型行列式的计算方法进行探讨，进而对不同特点的此类行列式我们得到一般的计算方法与计算公式。

例1 计算n阶行列式

分析：对于这个三对角线型行列式，三条对角线上的元素都是已知的，我们可以尝试利用消去法进行求解。

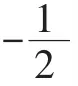
上面的行列式（1）是上三角形行列式，故Dn的值等于其主对角线元素的连乘积，即：

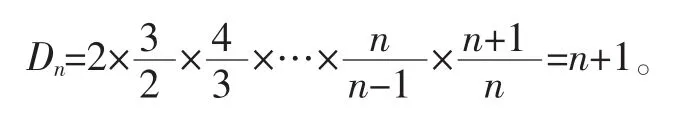
例2 计算n阶行列式

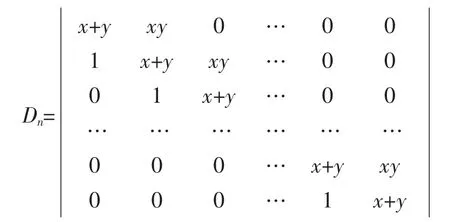
分析：对于此类三对角线型行列式，消去法就不再适用了，需要寻找其他方法来解决。通过观察，我们发现Dn与Dn-1、Dn-2具有相同的特点，因此我们想到行列式按一行或一列展开定理，将行列式降阶，进而利用递推公式法进行求解。

解 首先，将行列式Dn按照第一行展开，得：

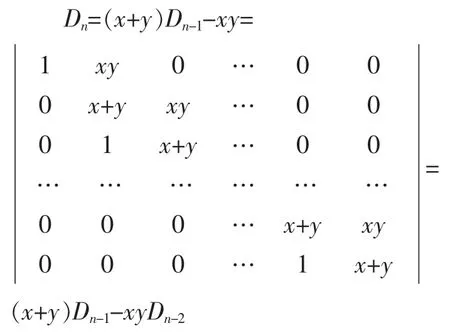
即得到Dn与Dn-1、Dn-2之间的一个关系式Dn=（x+ y）Dn-1-xyDn-2，将其变形为：

或：

这样就得到了我们想要的递推公式。由（2）式反复利用低阶代替高阶，可得：

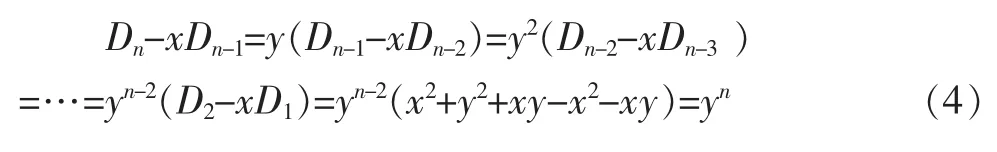
由（3）式反复利用低阶代替高阶，可得：

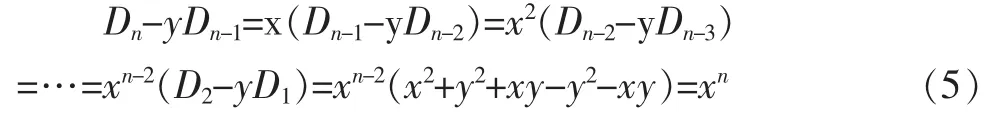
将（4）、（5）两式联立，即：

当x≠y时，解方程组（6）式，得：

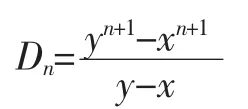
当x=y时，（4）式变为Dn-xDn-1=xn，即Dn=xDn-1+xn，反复利用此公式，将高阶替换为低阶，得到：

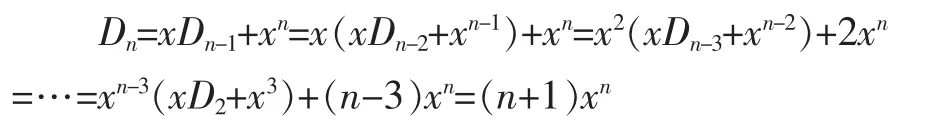
所以，行列式Dn的计算结果为:

对于这个行列式，虽然我们通过观察看出n阶与n-1阶有相同的结构，然后得到递推关系式，但我们不能盲目进行替换，一定要看清这个递推关系式是否可以简化我们的计算，如果不行的话，就要适当地变换递推关系式，得到我们想要的关系式，如本例题。

比较例1与例2可以看出，例1是例2的一个特殊情形，事实上，例1中的主对角线元素2可以看作2= 1+1，主对角线上方的元素可以看作1=1×1，即x+y=2, xy=1，也即x=1，y=1的情形。利用例2所得的公式（7），代入x，y的值自然可以得到例1的答案，即Dn=（n+1）xn=n+1，与消去法所得结果一致，但利用公式（7）进行求解方便很多。所以，例2可以作为一个典型的三对角线型例子，好多的此类行列式都可以套用公式（7）求解，既节省时间，结果又简单明了。需要注意的是例1、例2所给的三对角线型行列式并不包括所有的类型，例1、例2所对应的三对角线型行列式的主对角线下方的次对角线元素都是1，因此我们要进一步研究更一般的类型，得到一般的计算公式。

例3 计算n阶行列式

分析：此行列式比例2所给的行列式更具一般性，通过观察我们也可以用递推公式法进行求解。

解 将Dn按照第一行展开，得递推公式：

将（8）式看作：

或：

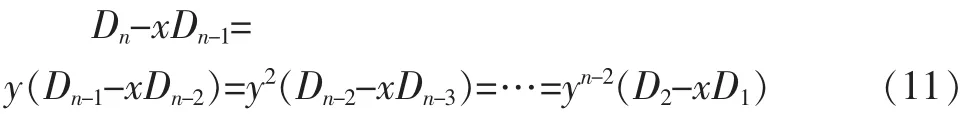
由（10）式反复利用递推公式，即可得：

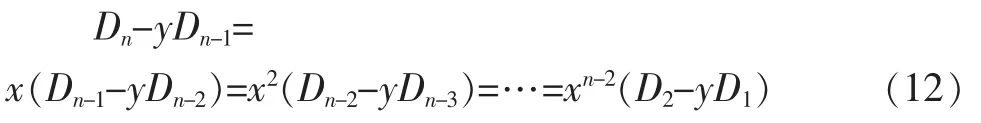
其中，D2=b2-ac=（x+y）2-xy，D1=b=x+y。因此，由（11）式可得：

由（12）式可得：

所以，当b2-4ac＞0，即x≠y时，联立（13）、（14）两式，可得：

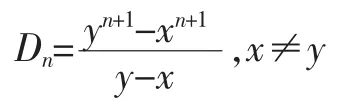
当b2-4ac=0，即x=y时，（9）式变为Dn-xDn-1=xn，即Dn=xDn-1+xn反复利用此递推公式，将高阶替换为低阶，得到：

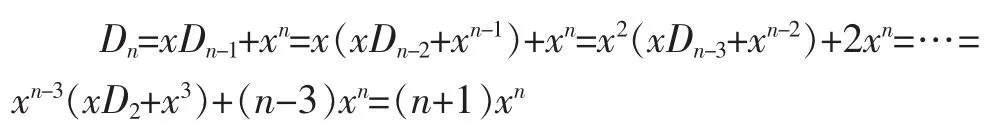
所以，

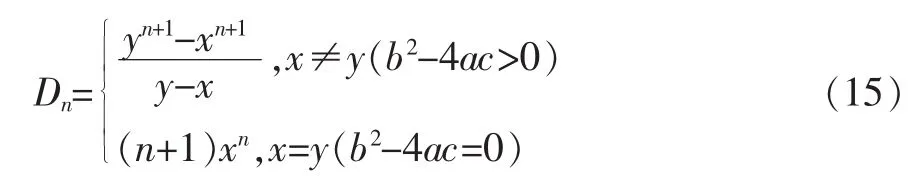
由于x，y是方程w2-bw+ac=0的两个实根，所以在具体计算时，只需将a，b，c代入方程，得到方程的实根，再代入公式（15），即可求得到三对角线型行列式Dn的值。

如行列式[2]：

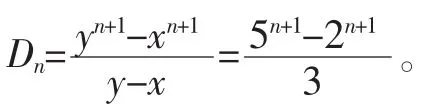
再如行列式[2]：

此行列式中a=-1，b=2，c=-1，满足b2-4ac=4-4=0，求解方程w2-2w+1=0得到实根x=y=1，所以套用公式（15）即得Dn=（n+1）xn=n+1。

例3所举的例子具有一般性，可以代表一类三对角线型行列式，但需要注意的是所给三条对角线的元素要满足b2-4ac≥0时，才可以用公式（15）进行求解，此公式也可以作为求解此类行列式的一般公式，但是对于b2-4ac＜0的情形还有待于进一步研究。

[1] 北京大学数学系.高等代数（第三版）[M].北京:高等教育出版社,2003

[2] 杨立英，李成群.n阶行列式的计算方法与技巧[J].广西师范学院学报（自然科学版），2006，23（1）：98～105

Solution Method of Tridiagonal Determinant

LI Hai-ying，ZHAO Jian-ying
（Department of Basic and Social Science,Inner Mongolia Business and Trade Vocational College,Huhhot 010022）

Tridiagonal determinant is a common and with special format determinant in the linear algebra,by the way of giving examples,discusses the computing method of this class determinant,and deduces it through the simple formal to the complex elements determinant.When the determinant elements satisfy a certain condition,obtains the computing method and computing formula of the general tridiagonal determinant.

Tridiagonal Determinant;Recursion Formula;Elimination Method

1007-1423（2015）02-0039-04

10.3969/j.issn.1007-1423.2015.02.010

李海英（1968-），女，内蒙古呼和浩特人，本科，副教授，研究方向为数学教育教学

赵建英（1966-），女，内蒙古呼和浩特人，本科，副教授，研究方向为数学教育教学

2014-11-27

2014-12-19