基于改进混合差分进化算法的输电网规划研究

黄 映

(南京供电公司，江苏南京210019)

输电网络扩展规划是根据负荷增长、电源规划方案以及现有网络结构和参数，确定输电网络的最佳扩展方案，以满足安全运行和经济性最优[1]。从数学上讲，电网扩展规划是一个带有大量约束条件的非线性整数规划问题，计算较复杂。鉴于输电网扩展规划问题的重要性，各国学者对其提出了许多求解方法，主要分为启发式方法、数学优化类方法[2]和智能优化方法三类[3，4]。

差分进化算法[5]（DE）是Storn和Price在1995年提出的一种在连续空间中进行启发式随机搜索的优化算法。该算法直接采用实数直接运算，不需要编码和解码操作，收敛速度快，稳定性好，其性能被证明要优于其他进化算法[6]。目前DE已成功应用于求解经济负荷分配[7]、无功优化[8]、变电站选址定容[9]等电力系统优化问题。虽然DE算法实现简单、收敛快速，但是该算法以随机概率选取试验个体进行进化，容易陷入局部最优，出现早熟收敛现象，若通过增加种群规模以提高种群多样性的方式会降低算法的收敛速度。为改善DE的性能，更好地解决电网规划问题，本文构造一种改进的混合差分进化算法（IHDE），进一步提高算法的收敛速度和全局寻优性能，并以Garver-6节点系统和18节点系统算例验证了此算法的寻优能力。

1 电网规划数学模型

本文在单阶段静态电网扩展规划问题中，主要考虑电网扩建的投资费用、固定运行维护费用以及系统年运行费用（即网损费用），在满足约束条件的情况下使总费用最小，规划方案能满足N-1检验。其各种费用的计算考虑了资金的时间价值，采用等年值费用法。模型采用的目标函数为：

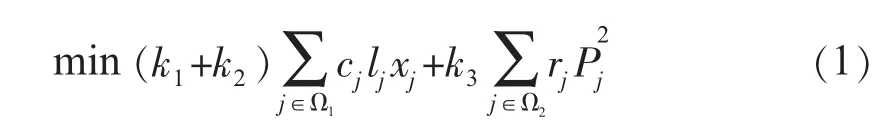
式（1）中：第一项为规划方案的建设投资费用，万元；第二项为线路的可变运行费用，用年网损费用表示，万元。其 中 k1为 资 金 回 收 系 数r为贴现率，%；n为工程经济使用年限；k2为工程固定运行费用率，%；cj为单位长度线路造价，万元/km；xj为线路j中新建线路回路数；lj为线路j的长度，km；Ω1为待选新建线路集合；k3为年网损费用系数；这里为网损电价，元 /（kW·h）；τ为最大负荷损耗时间，h；U 为系统额定电压，kV；rj为线路j的电阻；Pj为正常情况下线路j输送的有功功率，MW；Ω2为网络中已有的和新建的线路集合。

模型考虑的约束条件包括系统潮流约束，线路容量约束，输电走廊最大可建线路约束，其数学表达见文献[10]。潮流计算采用直流潮流模型。

2 差分进化算法及其改进

2.1 基本差分进化算法

差分进化算法由Np（种群规模）个D（决策变量个数）维参数矢量在搜索空间进行并行直接的搜索。DE的基本操作包括变异、交叉和选择3种操作。

（1）变异。

（2） 交叉。

（3）选择。对于最小化问题，选择操作可表述为：

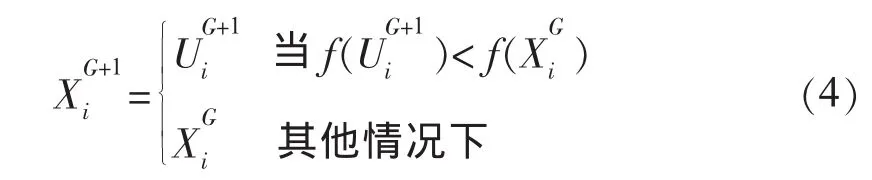
2.2 差分进化算法的改进

DE采用贪婪策略进行选择操作，虽然加快了算法的收敛速度，但在算法的后期收敛速度较慢,甚至会陷入局部最优出现早熟现象[11]。鉴于此，本文构造一种改进的混合差分进化算法（IHDE），该算法在求解过程中能够随进化过程动态调整DE的缩放因子和交叉概率，在保持种群多样性的同时提高DE的全局寻优能力；而针对DE早熟收敛问题，以种群的适应度方差判断种群中个体的聚集程度，引入混沌搜索策略，提高算法后期的搜索能力。

（1）控制参数的改进。DE算法的主要控制参数F和CR影响搜索过程的收敛速度和鲁棒性，F和CR取值较大可以得到较好的搜索但算法的收敛速度会较慢，取值较小会使算法陷入局部最优。良好的搜索策略应该是在搜索的初始阶段保持种群多样性，进行全局搜索，而在搜索的后期应加强局部搜索能力，以提高算法的精度。本文对F和CR采取根据进化代数动态调整策略，即在算法的初期取较小的F和CR，随着种群进化，不断增大两参数的取值，以保证其收敛性。

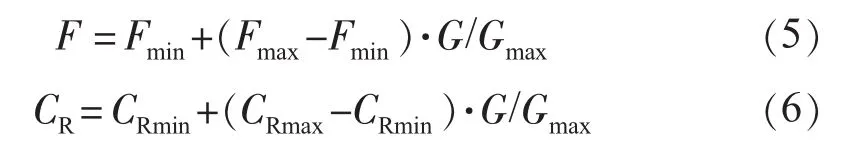
（2）种群适应度方差。随着种群的不断进化，个体之间的差异越来越小，而个体位置决定了个体的适应度，根据种群中所有个体的适应度的整体情况可以判断种群的状态。种群的适应度方差定义为：

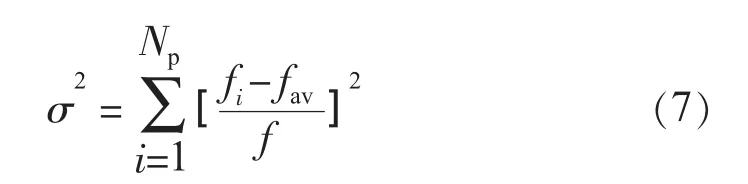
f的取值采用式为：

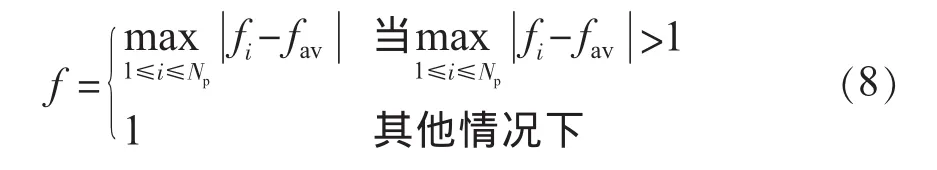
（3）混沌搜索策略。针对早熟收敛现象，本文在DE算法陷入局部最优时对当代最优个体进行混沌搜索，使算法脱离聚集状态。混沌是自然界广泛存在的一种非线性现象，由于混沌运动的固有特点及混沌遍历的规律性及不重复性，使混沌处理方法被广泛用于处理优化搜索问题[12]。混沌搜索常用的映射方式为线性载波：

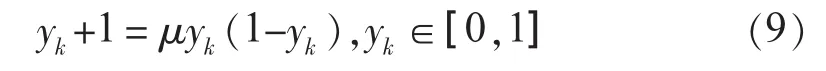
式（9）中：μ为控制参数，其数值直接影响映射情况；k为混沌搜索的迭代次数为混沌变量的各维分量。

2.3 改进混合差分进化算法流程

本文利用混沌搜索机制，并将其融合到差分进化算法中，构造了改进的混合差分算法（IHDE）。其基本思想是基于差分进化机制，动态调整其控制参数，以种群适应度方差判断算法是否出现早熟收敛现象，若陷入局部最优，则对当代最优个体进行混沌搜索，在搜索达到给定次数后，用混沌搜索得到的最优解随机替代种群中的个体，从而增强算法的搜索性能。该算法流程如图1所示。

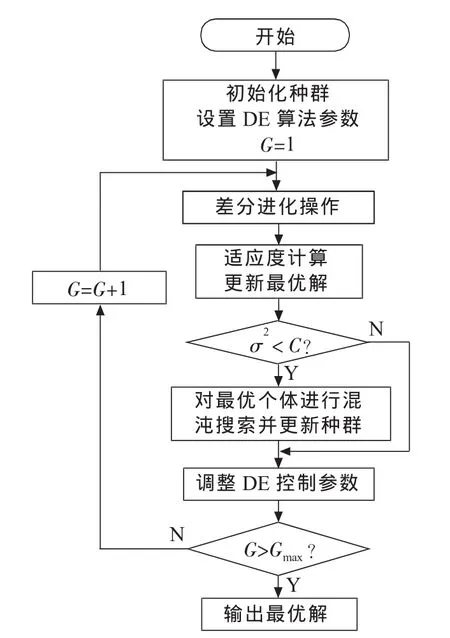
图1 IHDE算法流程图

3 基于改进混合差分的电网规划问题求解

基于上述改进的混合差分进化算法，对第1节描述的单价段输电网规划数学模型求解步骤：（1）输入原始数据。包括网络拓扑、线路参数、各节点发电出力及负荷以及算法本身需要的控制参数；（2）形成初始种群。本文对n条待选线路走廊的各种可能扩建回路数进行编码，n条待选线路走廊的扩建回路数集为该线路集构成一个规划方案，对应于种群中的一个个体；（3）差分进化操作。采用第2.1节中的变异和交叉机制形成新一代种群；（4）个体适应度计算。将每一个体对应的网络行潮流计算，若个体不满足约束条件的要求，则通过适应度中的惩罚项将个体自然淘汰，对满足约束的个体计算方案的投资和网损费用，进而求出个体的适应度值；（5）计算种群适应度方差，若σ2＜C，则对最优个体进行混沌搜索，否则到步骤（6）；（6）根据差分进化代数调整F和CR；（7）如满足中止条件，则到步骤（8），否则返回到步骤（3）；（8）输出规划结果。

4 算例及分析

以修改过的Garver-6节点和18节点系统为算例进行计算与分析，系统中节点数据、支路数据和可扩建走廊数参见文献[13]和文献[10]。设资金贴现率r取10%；工程经济使用年限n为15年，工程固定运行费用率k2为5%，网损电价ρ为0.3元/（kW·h），最大负荷损耗时间τ为3000 h，单位长度线路的投资费用为80万元/km，取单回线走廊宽度为48.27m，双回线走廊宽度为68.27m，三回线走廊宽度为88.27m，四回线走廊宽度为108.27m。

以MATLAB2007为仿真环境，对电网规划问题各进行50次计算，各算法求得平均计算时间和搜索成功率，如表1、表2所示。

6节点系统算例中，本文同时也利用GA，PSO算法进行了编程计算。表1列出各算法对在满足线路的N-1安全准则的条件下所求得的规划方案的投资维护费用、网损费用以及综合费用。其中文献[14]采用基于适应度函数值共享的小生境改进遗传算法求解该问题；文献[15]采用改进的带双重变异算子的粒子群算法求解该问题；而文献[16]采用基于精英策略的非支配排序遗传算法（NSGA-II），采用投资维护费用、网损费用和“N-1”过负荷量最小的多目标优化方法。文献[14—16]中3种改进算法的各部分费用均按本文设定的系数进行了折算作为比较。

由于18节点系统是按静态安全的“N”准则来研究输电规划的常用算例，因此对18节点系统设定各线路走廊的可架线路回数为3回，以使规划方案能够满足“N-1”安全准则。18节点系统的2种最优规划方案见表2，DE算法和本文采用的IHDE算法能够得到相同的2种最优方案，2种方案下的线路扩建结果虽略有不同，但费用相等。

IHDE和DE算法的种群适应度方差的变化曲线如图2所示。

由图2可见，IHDE算法在进化后期对最优个体进行混沌搜索，使种群脱离聚集状态，拓展了种群的搜索空间，改善了群体适应度方差的分布情况，避免算法陷入早熟收敛，从而有更好的全局寻优能力。

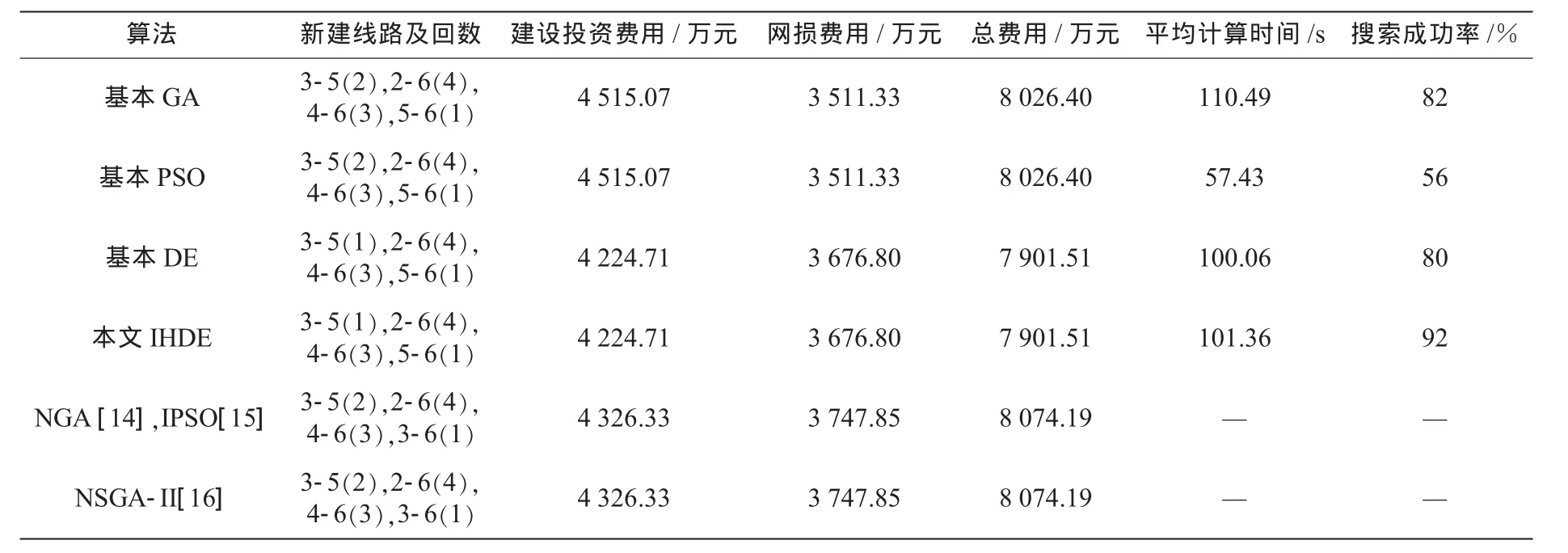
表1 6节点规划结果

表2 18节点规划结果

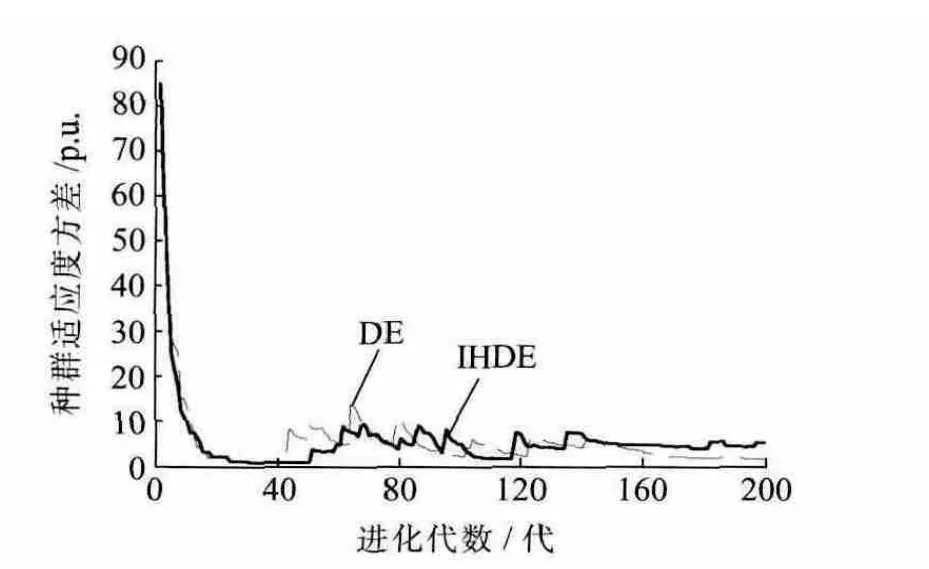
图2 IHDE和DE算法的群体适应度方差

图3展示了GA，PSO，DE以及IHDE 4种算法下的电网规划方案费用随种群进化代数的变化情况。

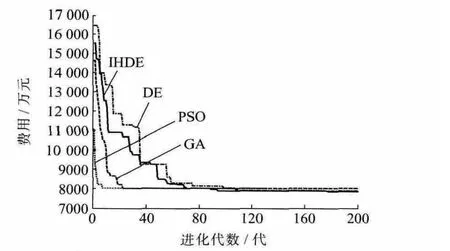
图3 几种算法的适应度进化曲线

综合表1、表2和图3可见，DE算法本身具有较好的寻优能力和搜索精度，DE及改进的IHDE算法在优化结果和算法性能上（如搜索时间和搜索成功率）都优于GA，PSO算法。比较IHDE算法和基本DE算法，虽然两者得到的最优结果相同，但是由于IHDE采用了控制参数调整和混沌搜索策略，IHDE算法性能更加稳定，搜索到最优解的成功率明显高于基本DE算法，且能够比DE算法更早求得最优解。而由于IHDE算法需要实时跟踪群体的聚集程度，其计算速度略不如基本DE算法。

5 结束语

本文提出了一种改进的IHDE算法，利用差分进化机制实现简单、收敛速度快的优点，对基本DE算法进行了改进。该算法能够随进化过程动态调整控制参数，进一步提高搜索性能；同时针对算法后期容易陷入局部最优的问题，以种群的适应度方差判断种群中个体的聚集程度，对最优个体采取混沌搜索。将IHDE算法应用于求解单阶段静态电网规划问题，通过对修改过的Garver-6节点系统和18节点系统的计算和分析表明，相对GA，PSO和基本DE算法，IHDE算法在搜索效率、计算精度、收敛稳定性、全局寻优能力等方面都有一定的优越性。

[1]麻常辉，薛禹胜，鲁庭瑞，等.输电规划方法的评述[J].电力系统自动化，2006，30(12)： 97-101.

[2]LATORRE G，CRUZ R D，AREIZA JM，et，al.Classification of Publication and Modelson Transmission Expansion Planning[J].IEEETranson PowerSystems，2003，18(2)： 938-946.

[3]GALLEGO R A，MONTICELLI A，ROMERO R.Transmission System Expansion Planningbyan Extended Genetic Algorithm[J].IEEE Proceedings： Generation，Transmission and Distribution，1998，145(3)： 329-335.

[4]金义雄，程浩忠，严健勇，等.基于局优分支优化的粒子群收敛保证算法及其在电网规划中的应用[J].中国电机工程学报，2005，25(23)：12-18.

[5]STORNR，PRICEK.DifferentialEvolution-a Simpleand Efficient Heuristic forGlobalOptimization OverContinuousSpaces，Technical Report TR-95-012[R].Berkeley：International Computer Science Institute，1995.

[6]MAYERDG，KINGHORNBP，ARCHERA A.DifferentialEvolution-An Easy and Efficient Evolutionary Algorithm for Model Optim ization[J].AgriculturalSystems，2005 ，83(3)：315-328.

[7]NOMAN N，IBA H.Differential Evolution for Economic Load Dispatch Problems[J].Electric Power SystemsResearch，2008，78(8)：1322-1331.

[8]刘自发，闫景信，张建华，等.基于改进微分进化算法的电力系统无功优化[J].电网技术，2007，31(18)：68-72.

[9]牛卫平，刘自发，张建华，等.基于GIS和微分进化算法的变电站选址及定容[J].电力系统自动化，2007，31(18)：82-86.

[10]程浩忠.电力系统规划[M].北京：中国电力出版社，2008：139-143，259-260.

[11]吴亮红，王耀南，袁小芳，等.自适应二次变异差分进化算法[J].控制与决策，2006，21(8)： 117-120.

[12]李 兵，蒋慰孙.混沌优化方法及其应用[J].控制理论与应用，1997，14(4)：613-615.

[13]RIDERM J，GAREIA A V.A Constructive Heuristic Algorithm to Short Term Transmission Network Expansion Planning[C].Power Engineering Society General Meeting， 2004 （2）：2107-2113.

[14]张振安，唐国庆.基于小生境技术改进遗传算法在供电网规划中的应用[J].江苏电机工程，2005，24(2)：30-33.

[15]CHEN Y H，CHEN H Y，CHEN JF，et，al.An Improved Particle Swarm Optimization Algorithm for Multistage and Coordinated Planning of Transm ission Systems[C].Transmission and Distribution Conferenceand Exhibition，Asiaand Pacific，2005.

[16]王秀丽，李淑慧，陈皓勇，等.基于非支配遗传算法及协同进化算法的多目标多区域电网规划[J].中国电机工程学报，2006，26(12)：11-15.