非均匀介质中超声场仿真研究*

李 雅，陈友兴，王召巴

(中北大学信息与通信工程学院，山西太原030051)

在无损检测工业技术中，超声检测作为其中一种既安全又经济的手段，在探伤研究领域深受工程技术人员的青睐，其中超声场的分布关系到缺陷的检出和定位定量的可靠性和准确性，因此准确的计算探头发射声场是定量研究超声传播过程的基础［1～4］。

工业超声检测构件内部缺陷时，常利用侵水式超声脉冲反射法进行探伤研究。由于构件表面的不平整性和空气中能量损失较大，以水为耦合介质能够很好的与构件表面贴合。探头发射超声波利用水中传播到达构件，有效的减小声能量在空气中的损失，有利于得到较强的反射回波信号，用来研究判断构件内部的结构。本文根据这一研究背景，设计了水和构件的非均匀介质中的超声场模型，用于更加直观，细微的观测声场在构件内部的传播特性及其分布规律［5］。

1 倾斜入射时的声场模型

当超声波倾斜入射至异界面上，且第二介质为固体时，则透射波会发生波形的转换，分为折射纵波和折射横波，两种折射波沿着各自的传播方向传播，且不同于入射波方向［7～10］。

折射波的折射角按几何光学中的折射定律确定(入射波为纵波):

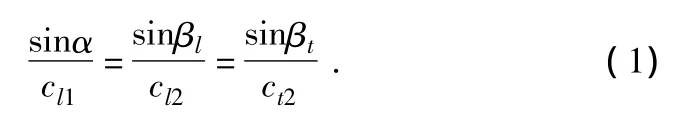
其中，α为纵波入射角;βl为纵波折射角;βt为横波折射角;cl1为入射波在第一介质中的声速;cl2为折射纵波在第二介质中的声速;ct2为折射横波在第二介质中的声速。

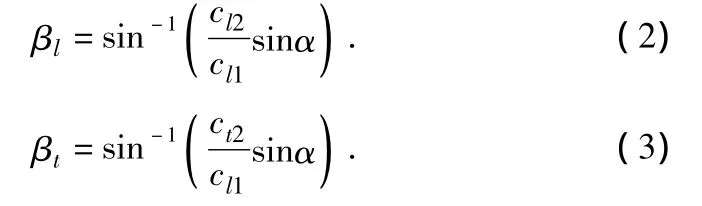
如图1(a)所示，当以纵波入射，且cl1＜cl2(即本文所研究的超声纵波声束从水中倾斜入射至钢中)，超声声束在第二介质中发生波形的转换分为折射纵波和折射横波，分别用L和T表示。由式(3.4)可知 βl＞α，且 βl随着 α 的增大而增大。

当βl=90°时(图1(b)所示)，此时的纵波入射角为第一临界角，用αI表示，可知当入射角大于第一临界角时，第二介质中只有折射横波存在。

若cl1＜ct2，则 βt＞α，且 βt随着 α 的增大而增大。

当βt=90°时，如图1(c)所示，此时入射角为第二临界角，用αⅡ表示，可知当入射角大于第二临界角时，第二介质中不存在折射波。

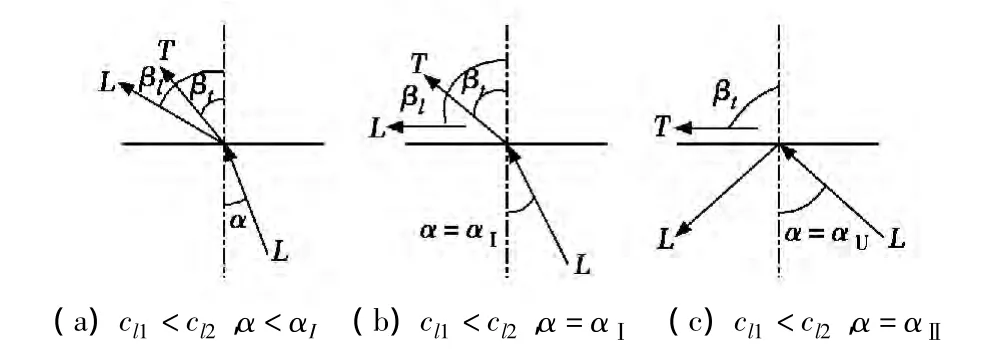
图1 超声波传播示意图

如图2所示为聚焦探头在水做耦合介质的环境中发射超声波达到长方形介质的声场分布示意图。本文分别研究了纵波和横波不同声场分布特性。参数设定如下:水的密度为1 000 kg/m3，水中纵波声速为1 400 m/s，横波在水中不存在设为0 m/s，黑色区域的密度为1 850 kg/m3，纵波声速为3 000 m/s，横波声速为1 400 m/s。(下文其他结构的参数设定相同)

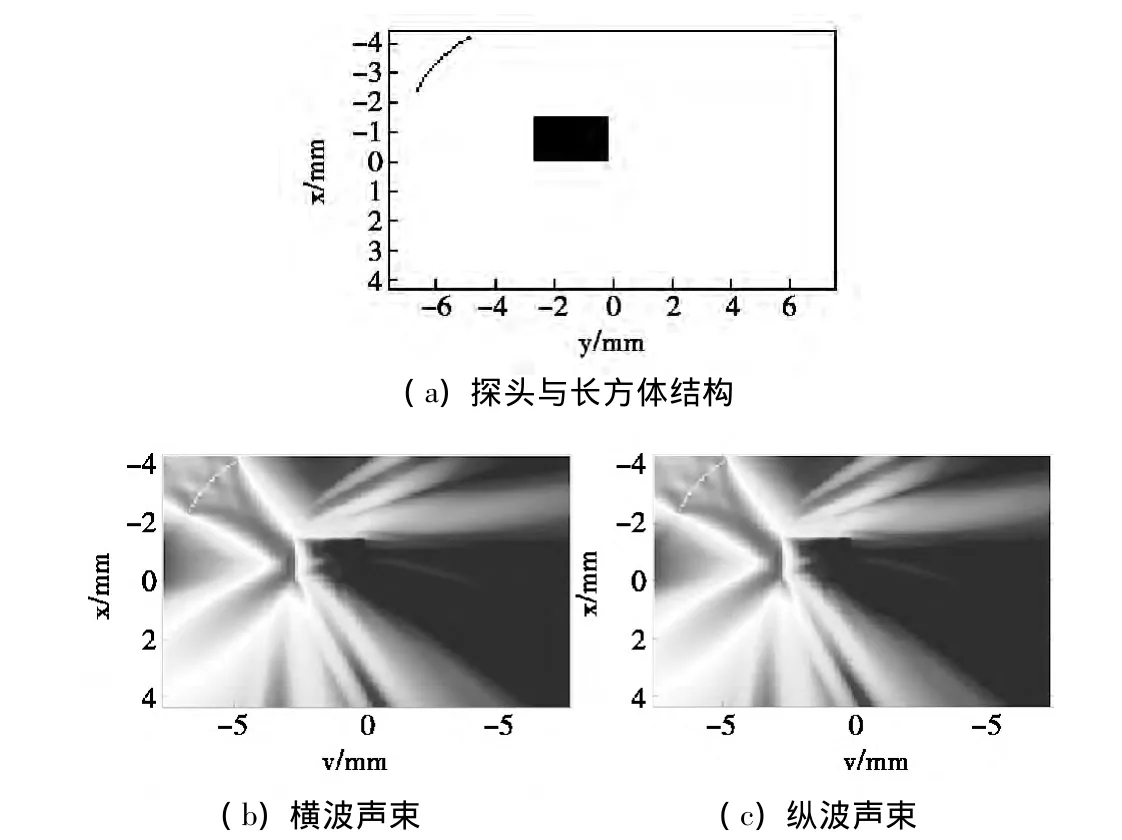
图2 聚焦探头、纵波、横波不同声场分布示意图

2 曲面对声场分布的影响

本文所研究的圆环和偏心缺陷圆结构，其表面是有一定的曲率，因此研究曲率对活塞探头声场分布的影响也非常重要［8］。水侵式超声检测时，界面处的曲率会直接影响工件中的声压分布。如图3超声声波在透过曲界面时的反射和折射原理图所示:

图3 超声波在曲界面处的反射和折射原理

由上图可以看出，曲界面对相邻介质透射波起的作用，就相当于光学中聚焦透镜与发散透镜作用一样。曲界面对于超声声束的作用规律为，当超声声束由声阻抗小的介质射向声阻抗大的介质时(即从水中射入钢中)，从固体一侧观察，凹界面对超声声束起到汇聚的作用，如图3(c)，凸界面对超声声束起到发散的作用，如图3(d)。

如图4所示为聚焦探头垂直入射到圆环结构上的横纵波声束示意图。可以明显的看到声束在上半圆凸曲面的发散效果，和下半圆凹曲面的汇聚效果。

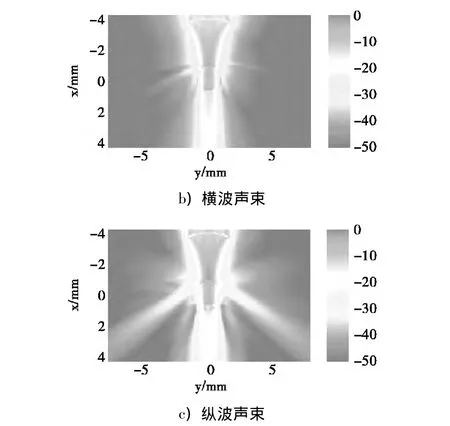
图4 圆环声压分布特性

3 超声经过圆界面的分布特性

工业中很多构件的结构都是圆柱结构，如螺钉、机械轴，关节臂的连接接口等等。这些圆柱体构件的内部损坏会大大影响工业的正常生产。本文针对偏心缺陷圆结构进行了声场模型的进一步研究。对其内部声场的分布进行了可视化仿真研究。

如图5(a)所示的偏心缺陷圆结构与聚焦探头的示意图。图5(b)是超声波的全波束显示效果图。由于横波只能在固体介质中传播，不能在液体介质中传播，图5(b)显示了超声波在介质中的声束分布特性。可以看到在固体、液体中传播的声束，有着明显的汇聚和分散特性，且超声声束在通过凹界面时声能汇聚并在圆形缺陷处声压值迅速增大，此时有利于缺陷的探伤。

图5 偏心缺陷圆声压分布特性

4 总结

本文主要研究了声场在三种典型结构中的传播特性和分布规律:

1)在长方体平面结构中的声束传播过程中非均匀截面处存在着横纵波转换特性;2)圆环结构中曲面结构对声束有着明显的汇聚和分散特性;3)偏心缺陷圆结构中，超声束在通过凹界面时声能汇聚并在圆形缺陷处声压值迅速增大，此时有利于缺陷的探伤。本文对声场可视化的仿真研究为工业生产应用奠定了更加完善的研究基础。

［1］Wen JJ，Breazeale MA.A diffraction beam field expressed as the super position of Gaussian beams［J］.Acoustical Society of America，1989，83(5):1752 －1756.

［2］孟凡凯.水下超声波检测声场数值模拟与实验分析［D］.哈尔滨工业大学，2012:4－16.

［3］沙正骁，刚铁，赵新玉.超声换能器声场的模拟和可视化研究［J］.无损检测，2011，33(5):2－6.

［4］丁辉.计算超声学:声场分析及应用［M］.北京科学出版社，2010:23－26.

［5］杜宏伟，陆伟.Gauss聚焦脉冲波非线性声场特性［J］.中国科学技术大学学报，2010，40(3):299－305.

［6］先永利.有限声束非线性超声场的快速计算及其特性研究［D］.中国科学技术大学，2011:5－20.

［7］朱宏，丁德胜.高斯展开法计算各向异性介质中的声场分布［J］.电子器件，2007，30(1):180 －182，185.

［8］章东，许阳，郭霞生.一种相控阵非线性声场的定量确定方法［P］.江苏:CN103170068A，2013:3－4.

［9］涂海华，陶向阳.硬边光阑的复高斯函数展开及在高斯光束中的应用［J］.江西师范大学学报(自然科学版)，2004，28(1):52 －56.

［10］蒙海英.基于MATLAB的超声波声场模拟及可视化研究［D］.大连理工大学，2008:13－30.