Ti35合金管材数控弯曲成形规律有限元模拟研究
2015-05-12宋飞飞吴金平杨英丽罗媛媛郭荻子
宋飞飞,吴金平,杨英丽,赵 彬,罗媛媛,郭荻子
(西北有色金属研究院,陕西 西安 710016)
Ti35合金管材数控弯曲成形规律有限元模拟研究
宋飞飞,吴金平,杨英丽,赵 彬,罗媛媛,郭荻子
(西北有色金属研究院,陕西 西安 710016)
利用Abaqus有限元软件对新型耐蚀Ti35合金管材的数控弯曲过程进行了模拟研究。研究了弯曲角度、芯棒伸出量、压块相对助推速度和相对弯曲半径对Ti35合金管材成形结果的影响。结果表明,Ti35合金管材数控弯曲截面扁化率和回弹角随弯曲角度的增大而增大;弯曲变形越剧烈(如减小弯曲半径、压块相对助推速度,或增大芯棒伸出量),壁厚减薄率越大,回弹角越小。截面扁化率随芯棒伸出量、相对弯曲半径的增大而减小。
Ti35合金;钛合金管;数控弯曲;有限元模拟
0 引言
在石油、煤、天然气等石化能源日趋紧张的今天,核能以其能量密集、功率高、清洁等优点正逐渐成为传统石化能源的替代品。核乏燃料后处理在核工业燃料循环体系中占有重要地位,其主要目的是回收宝贵的裂变燃料[1],由于核乏燃料后处理关键设备长期在强酸性与放射性环境中工作,其关键设备用材料的研发受到许多学者的关注[2-3]。钛及钛合金很容易与氧结合生成氧化膜,在硝酸、浓硫酸等存在氧化剂的溶液中可以保持钝化,具有优良的耐蚀性。Ti35合金是一种Ti-Ta系二元α型钛合金,具有良好的加工性能及耐腐蚀性能,特别在具有氧化性阳离子的核乏燃料模拟料液环境中,其腐蚀速率<0.01 mm/a,耐腐蚀性能优异,作为超低碳不锈钢的替代材料,具有在核乏燃料后处理关键设备上应用的巨大前景[4]。
作为一种新型的设备用材,Ti35合金管材主要应用于换热管和料液管路或管道等部位,其中管路或管道必然存在弯曲的部分。数控弯管技术以其能够实现管材批量、快速生产的特点,被广泛应用于管材的弯曲成形制造当中[5]。然而,管材弯曲后会发生管壁减薄、截面扁化及回弹等现象,这些现象如果过度显著,超过使用要求,就会成为成形缺陷,如弯曲外侧断裂、截面扁化严重、弯曲内侧起皱严重及过度回弹等。相比于不锈钢,钛合金屈强比高,造成塑性加工区间小,屈弹比高,造成回弹更加显著[6],其管材弯曲性能及成形质量严重影响管路或管道的使用性能。因此,有必要对Ti35合金管材的弯曲性能进行系统研究,从而为工业化应用Ti35合金设备的设计提供相关依据。
1 研究方法
1.1 三维弹塑性有限元建模
数控弯管成形是多模具耦合作用的复杂非线性过程(如图1所示),理论解析法因存在假设而导致研究精度有限,实验法又耗费大量人力物力,而有限元法因可以处理复杂非线性过程,成为处理该问题的最佳选择。基于Abaqus软件,兼顾计算精度和计算效率,对管材弯曲和回弹过程分别采用动态显式(Dynamic,Explicit)和静态隐式(Static,General)算法求解。管材选择六面体8节点减缩积分实体单元(C3D8R),该单元具有沙漏控制和减缩积分功能,厚度方向选择4个积分点来满足精度要求。模具选择离散刚体单元(R3D4)。对不同模具与管材间的摩擦采用库伦摩擦模型描述接触面间的摩擦行为,对管材内表面与芯棒、外表面与模具的接触分别采用罚函数法和动态约束算法。考虑到管材弯曲对称性,采用半管模型进行计算。在网格划分问题上,为了提高计算精度,对管材的弯曲变形区划分较细的网格,而对各模具以及非变形区的管材采用较粗的网格进行划分[7]。

图1 管材数控弯曲示意图Fig.1 Principle of tube NC bending
依据 GB/T 228—2010,对规格为 φ30 mm×4 mm的Ti35合金管进行整管室温拉伸试验,试验设备为INSTRON 5985万能材料试验机。获得管材拉伸曲线后,采用幂指数化加工硬化模型σ=k(ε-a)n来拟合管材屈服后的应力应变行为,试验及拟合结果如表1所示,该数据将录入软件材料模型中来描述变形行为。

表1 Ti35合金管材料参数Table 1 Material parameters of Ti35 tube
1.2 试验方案
采用单因素法进行研究,选取的工艺参数均对弯曲结果有显著影响,包括弯曲角度α、芯棒伸出量e、压块相对助推速度Vp/V和相对弯曲半径R/D,每因素至少采用3水平,如表2所示,其中粗体为默认设置。考察的指标包括Ti35合金管材弯曲过程中的缺陷形式,是否有起皱、凸包、破裂及其它缺陷出现。如果可以顺利弯曲成形,则要考察弯曲后管材的形状尺寸精度和性能,包括外脊线的壁厚、圆度、回弹等。

表2 Ti35合金管材数控弯曲工艺参数模拟方案Table 2 Simulation scheme of forming parameters for Ti35 alloy tube numerical-control bending
1.3 结果表征方法
Ti35合金管材弯曲后的圆度可以用截面扁化率表征,外脊线的壁厚可以用壁厚减薄率表征。采样频率为从弯曲起始面至弯曲终止面,每隔几度的测量结果,其计算方法分别如式(1)、(2)所示。弯曲回弹可以用回弹角来表征,即弯曲角度与回弹后的最终成形角度的差值,如式(3)所示。

式中,D0和D1分别为Ti35合金管材弯曲前外径和弯曲后短轴长度,t0和t1分别为弯曲前壁厚及弯曲后外脊线处壁厚,α0和α1分别为弯曲角度和成形角度。
2 结果与讨论
2.1 不同弯曲角度的影响

图2 弯曲角度对壁厚减薄率、截面扁化率和回弹角的影响Fig.2 Effect of bending angle on wall thinning ratio,ovalization ratio and springback angle
管材在弯曲变形时,外侧脊线承受最大的拉应力,因此,选择对管材外脊线处的壁厚进行测量。图2a为不同弯曲角度下管材外脊线处的壁厚减薄率变化规律。可以看出,不同弯曲角度下,壁厚减薄率的变化趋势是一致的,最大壁厚减薄发生部位均靠近弯曲后端。因为弯曲后端得到芯棒的支撑,在芯棒的作用下,此处管材应力状态更为复杂,减薄率较大。图2b是弯曲角对截面扁化率的影响图,可以看出,截面最大扁化率随弯曲角的增加而增大,这是因为弯曲角越大,变形区域越大,芯棒对管材的支撑作用就相对减弱,引起扁化率增大。通过隐式算法求解回弹过程,图2c所示为不同弯曲角度下的回弹角变化规律,可以看出回弹角随弯曲角的增大而增大,且和弯曲角基本呈线性关系。实践中常通过该规律,对实际控制成形角进行指导[8],即首先进行20°、120°弯曲,拟合出回弹角-弯曲角关系曲线,再根据所要成形的角度,反推出弯曲角度。
2.2 芯棒伸出量的影响
图3a为芯棒伸出量对壁厚减薄率的影响图。从图中可以看出壁厚减薄率在整个弯曲段变化不大,随着芯棒伸出量的增大,最大减薄率逐渐增大。这是因为随着芯棒伸出量的增加,阻碍了材料顺利越过弯曲切点向前流动,这样在后续的弯曲过程中,由于没有后续材料的补偿,外侧因受拉应力而产生的壁厚减薄就会加剧。图3b为芯棒伸出量对截面扁化率的影响图。从图中可以看出,不同芯棒伸出量下的管材截面扁化率的变化规律相同,即截面扁化率从夹块端到压块端都是逐渐增加。随着芯棒伸出量的增加,截面扁化率整体上呈减小的趋势。这是因为增加芯棒伸出量就增加了管材内壁受到的支撑,从而有助于减小弯管截面扁化。

图3 芯棒伸出量对壁厚减薄率、截面扁化率和回弹角的影响Fig.3 Effect of mandrel protrusion length on wall thinning ratio,ovalization ratio and springback angle
图3c是芯棒伸出量对回弹角的影响图。从图中可以看出,随着芯棒伸出量的增加回弹角呈减小趋势。这是因为芯棒伸出量增大,使弯曲段外侧受拉应力增大,拉应力可以减小回弹[8]。
2.3 压块相对助推速度的影响
图4a为压块相对助推速度对壁厚减薄率的影响图,可以看出,当压块相对助推速度为0.9时,壁厚减薄率明显大于压块相对助推速度大于等于1时的壁厚减薄率。这是因为当压块速度小于弯曲速度时,压块对管材的摩擦力与管材移动方向相反,这样就增大了管材外壁受到的拉应力,使得外侧壁厚减薄率增大。当压块速度与弯曲速度相等或大于弯曲速度时,压块对管材向后的摩擦力消失,改善管材外壁受所受拉应力起到侧推作用,从而减小壁厚减薄。当压块相对助推速度大于1时壁厚减薄率略有减小。图4b为压块相对助推速度对截面扁化率的影响图,从图中可以看出当压块相对助推速度为0.9时截面扁化率明显增大,当压块相对助推速度大于1时截面扁化率略微减小,且当压块相对助推速度大于等于1时,截面扁化率变化不大。图4c为压块相对助推速度对回弹角影响图,从图中可以看出,回弹角在压块相对助推速度为0.9时,回弹角最小,这是因为小于1的压块相对助推速度在管材弯曲过程中实际施加了向后的拉力,弯曲切向拉力可以减小回弹角。当压块相对助推速度大于1时,回弹角随压块相对助推速度的增大略微增大。
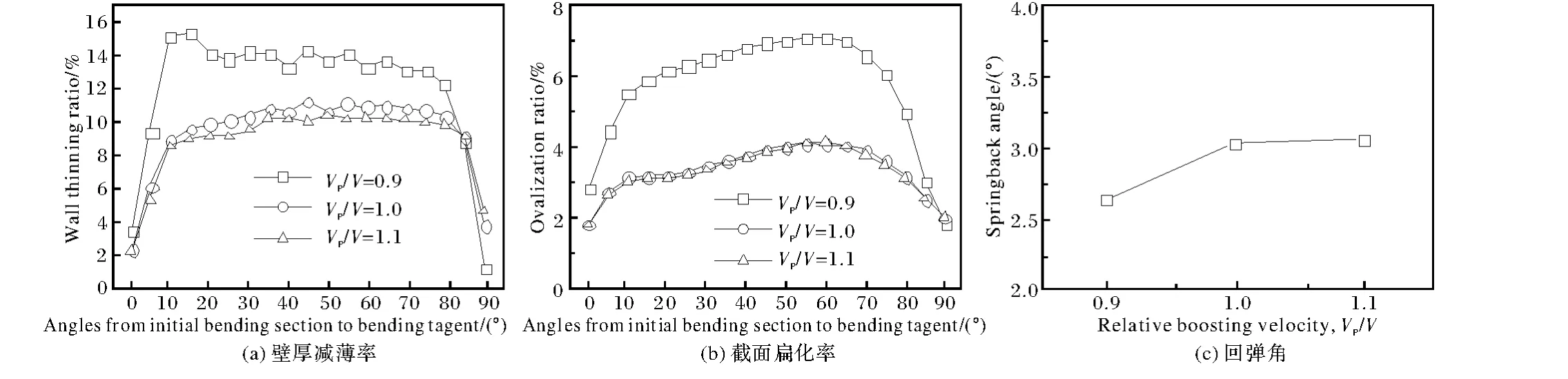
图4 压块相对助推速度对壁厚减薄率、截面扁化率和回弹角的影响Fig.4 Effect of relative boosting velocity on wall thinning ratio,ovalization ratio and springback angle
2.4 相对弯曲半径的影响
图5a为相对弯曲半径对壁厚减薄率的影响图,从图中可以看出随着相对弯曲半径的增大,壁厚减薄率逐渐减小。这是因为大的相对弯曲半径下,同样弯曲角度下变形量相对较小,因此壁厚减薄率也较小。图5b为相对弯曲半径对截面扁化率的影响图,可以看出随着相对弯曲半径的增大,截面扁化率逐渐减小。规律与壁厚减薄率变化一致。图5c为相对弯曲半径对回弹角的影响图。可以看出,回弹角随相对弯曲半径的增大而增大,这是因为相对弯曲半径增大,同样变形中的弹性变形增大,导致卸载后回弹角增大。

图5 相对弯曲半径对壁厚减薄率、截面扁化率和回弹角的影响Fig.5 Effect of relative bending radius on wall thinning ratio,ovalization ratio and springback angle
3 结论
(1)弯曲角度对Ti35合金管数控弯曲壁厚减薄率影响较小。随着弯曲角度增大,截面扁化率增大,且回弹角与弯曲角度呈正比例增长关系。
(2)Ti35合金管材弯曲变形越剧烈(如减小相对弯曲半径、增大芯棒伸出量,或降低压块相对助推速度),壁厚减薄率越大、回弹角越小。截面扁化率随芯棒伸出量、相对弯曲半径的增大而减小。当压块相对助推速度小于1时,壁厚减薄率及截面扁化率明显增大,但回弹角减小。
(3)通过有限元模拟,可以优化Ti35合金管材数控弯曲成形工艺参数,减小试验次数,降低人力和物力成本,提高Ti35合金管材弯曲成形精度和效率。
[1]徐潇潇,邱邵宇.Ti合金在核燃料后处理设备中的应用研究进展[J].材料导报,2005,19(11):57-59.
[2]Dey P K,Bansal N K.Spent fuel reprocessing:a vital link in Indian nuclear power program[J].Nuclear Engineering and Design,2006,236(7/8):723-729.
[3]Baldev Raj,Kamachi Mudali U.Materials development and corrosion problems in nuclear fuel reprocessing plants[J].Progress in Muclear Energy,2006,48(4):283 -313.
[4]吴金平,杨英丽,奚正平,等.Ti35合金焊接接头在高温硝酸中的腐蚀性能研究[J].钛工业进展,2012,29(1):22-25.
[5]Jiang Z Q,Yang H,Zhan M.Establishment of a 3D FE model for the bending of a titanium alloy tube[J].International Journal of Mechnical Sciences,2010,52(9):1115 -1124.
[6]Yang H,Li H,Zhang Z Y,et al.Advances and Trends on Tube bending Forming Technologies[J].Chinese Journal of Aeronautics,2012,25(1):1 -12.
[7]Song F F,Yang H,Li H,et al.Springback prediction of thick-walled high-strength titanium tube bending[J].Chinese Journal of Aeronautics,2013,26(5):1336 -1345.
[8]宋飞飞,杨合,杨英丽,等.钛合金管冷弯回弹及其控制研究现状[J].钛工业进展,2014,31(6):7-11.
Finite Element Simulation of Forming Rules of Ti35 Alloy Tube Numerical Control Bending
Song Feifei,Wu Jinping,Yang Yingli,Zhao Bin,Luo Yuanyuan,Guo Dizi
(Northwest Institute for Nonferrous Metal Research,Xi’an 710016,China)
The numerical-control(NC)bending process of new corrosion-resistant Ti35 alloy tube is numerical analyzed using finite element(FE)software Abaqus.In the simulation,the effects of bending angle,mandrel protrusion length,relative boosting velocity and relative bending radius on forming process of Ti35 alloy tube were investigated.It is observed that the thickness thinning ratio is increasing,while the springback angle is decreasing when intensifying the bend forming,such as decrease the bending radius and relative boosting velocity,or increase the mandrel protrusion length.The mandrel protrusion length and relative bending radius have the negative effect.FE simulation can effectively decrease the manpower and material resource costs,and it also provides some reference for further industrialized application of Ti35 alloy.
Ti35 alloy;titanium alloy tube;NC bending;FE simulation
10.13567/j.cnki.issn1009-9964.2015.04.005
2015-05-07
陕西省重点科技创新团队计划“钛合金研发创新团队”(2012KCT-23)
宋飞飞(1987—),男,助理工程师。
