混沌相幅变换耦合像素替代的图像加密算法研究

乔立龙， 杨志敏

(1. 山东外事翻译职业学院工程技术学院, 山东 威海 264504；2. 山东大学计算机科学系， 山东 威海 264209)

混沌相幅变换耦合像素替代的图像加密算法研究

乔立龙1， 杨志敏2

(1. 山东外事翻译职业学院工程技术学院, 山东 威海 264504；2. 山东大学计算机科学系， 山东 威海 264209)

为有效保护图像在开放的网络环境中安全传输， 防止信息被窃取， 设计了混沌相幅变换算子耦合像素替代的图像加密算法. 首先将256 bit的外部密钥分割为8个子块， 以此设计迭代函数初始参数的估算模型， 从而生成两个密钥； 引入离散傅里叶变换， 将图像转变成相与幅度成分； 基于第一个密钥， 通过迭代Tent映射， 生成伪随机图像的相与幅度， 并构造线性叠加模型， 将明文与随机图像的相与幅度叠加， 借助逆离散傅里叶变换， 得到置乱图像； 再根据第二密钥， 基于Logistic映射， 设计像素替代模型， 改变置乱图像的像素值， 在时域与频域内同步完成加密. 仿真实验结果显示该算法具有较高的安全性， 能够有效抵御明文攻击, 与当前单域图像加密算法相比， 具有更高的加密效率.

图像加密； 离散傅里叶变换； 外部密钥； 幅度变换； 像素替代

0 引言

随着计算机技术与互联网应用技术的快速发展和交互渗透， 多媒体技术已成为人们进行信息交流的常用技术， 进而网络信息安全也成为大众研究的焦点[1]. 图像作为多媒体技术强有力的表达方式之一， 其中包含了大量信息， 也是人们日常生活中最直观的交流载体， 给人们的生活与沟通带来很大的便利[2]. 然而， 当前网络环境下， 图像信息的安全传输存在着一定的风险， 图像在传输过程中易遭受攻击者的破译， 致使其内容信息被窃取， 给用户带来后续隐患[3]. 为了有效确保图像的安全传送， 各国研究学者提出了数据加密技术， 但是传统的经典加密算法， 如数据加密标准DES、 IDEA算法以及RSA算法等， 没有考虑到图像具有大数据容量、 冗余度较高等特点， 因此将其应用于图像加密会存在较大的不足[4]. 对此， 为了适应信息安全的需求， 研究人员相继开发了诸多图像信息加密算法. 如Himan等[5]为了增强算法的安全性， 设计了基于随机位序列的混沌图像加密算法， 利用Logistic与Tent映射生成随机位序列， 利用该序列对图像完成扩散， 实验结果表明其算法具有较高的安全性； 该算法是典型的时域加密机制， 只对图像的时域进行加密， 但其安全性仍可进一步完善. Ashutosh等[6]为了提高算法的鲁棒性， 提出了图像频域加密思想， 设计了随机相掩码与离散傅里叶变换的高鲁棒性图像加密算法， 通过两个随机矩阵， 联合离散傅里叶变换， 实现图像像素扩散， 仿真结果显示其算法具有较强的鲁棒性， 在缺少正确密钥的条件下， 是无法破译图像的； 该技术是一种先进的频域加密技术， 但只对图像频域完成加密， 其安全性仍可进一步提高. 为了充分利用图像的空域、 时域与频域的优势， 肖迪等[7]提出一种空域和频域相结合的加密算法， 首先在空域对8×8分块进行扩散置乱， 然后利用边缘检测手段找出包含细节信息较多的重要分块， 先加密所有分块中的直流系数， 再选择重要分块中的一部分交流系数进行加密, 最后将分块重要性标记信息嵌入AC系数中进行传输， 实验结果验证了算法的合理性与优异性.

根据文献[8]可知， 充分利用空域、 时域与频域的优势， 可以进一步改善算法的鲁棒性. 在该思想的基础上， 充分利用时域与频域的优势， 提出混沌相幅变换算子耦合像素替代的图像加密算法. 通过离散傅里叶变换， 将图像转变成相与幅度成分， 由迭代Tent映射， 生成相变换与幅度变换算子， 完成图像频域加密； 再设计像素替代模型， 完成时域加密. 最后测试频域-时域加密技术与当前单域加密技术的安全性.

1 双域加密算法设计

图像加密算法见图1. 算法包括2个单元： ① 混沌相-幅度变换单元， 见图2; ② 混沌像素替代单元， 见图3. 通过将256位的外部密钥分割为8个子块， 以生成两个密钥； 再通过离散傅里叶变换， 将图像转变成相与幅度成分， 再基于第一个密钥， 由迭代Tent映射， 生成伪随机图像的相与幅度， 并构造线性叠加模型， 将明文与随机图像的相与幅度叠加， 借助逆离散傅里叶变换， 得到置乱图像； 再根据第二个密钥， 基于Logistic映射， 设计像素替代模型， 改变置乱图像的像素值， 在时域与频域内同步完成加密.

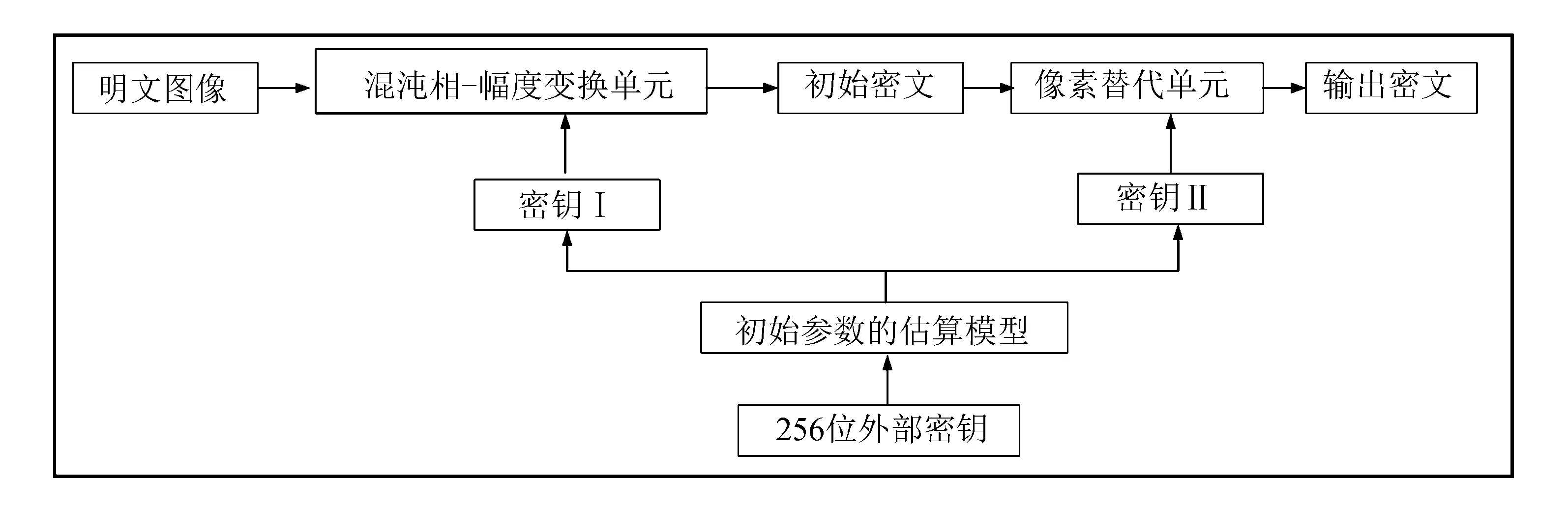
图1 算法流程

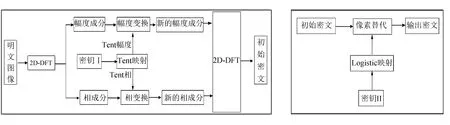
图2 混沌相-幅度变换单元流程图 图3 像素替代单元流程图

1.1 混沌相-幅度变换单元

为了提高算法的复杂性， 利用256 bit的外部密钥K来迭代生成Tent、 Logistic映射的初始条件. 将外部密钥K分割为32比特的8个子块：

随后， 定义迭代函数， 生成Tent、 Logistic映射的初始条件：

其中:XTent，XLogistic分别代表Tent、 Logistic映射的初始条件.

若明文图像I的尺寸为M×N， 引入2D离散傅里叶变换(DFT-discrete fourier transform)， 生成相成分与幅度成分：

公式(4)中， 图像的频域由函数F(u,v)来表示， 函数f(x,y)表示图像I的灰度等级；x=0, 1, 2, …,M-1、y=0, 1, 2, …,N-1为像素坐标.

令函数R(u,v)与W(u,v)分别表示F(u,v)的实部与虚部， 则该变换的傅里叶频谱与相位角为：

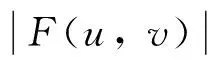
则模型(4)可演变为：

再利用Tent映射生成伪随机图像. 其模型如下：

再根据模型(1)， 计算Tent映射的初值X0与控制参数P， 初值X0的计算见模型(2)， 而P的计算模型为：

通过迭代模型(8)， 可得伪随机Tent图像. 以图4(a)为明文， 其直方图见图4(b)， 经过模型(4)处理后， 得到的相成分与幅度成分， 分别见图4(c)和图4(d). 而迭代模型(8)后， 经过模型(4)变换后， 生成的Tent混沌相与幅度见图5(a)和5(b)， 最终生成的初始密文及其直方图见图5(c)与图5(d).

图4 明文图像的2D傅里叶变换

图5 Tent图像的2D傅里叶变换

若明文图像经模型(4)变换后， 产生的相与幅度频谱分别用PPI与MPI表示； 而Tent图像的相与幅度频谱分别用PTI与MTI表示， 则构造线性叠加模型， 生成新的相与幅度：

其中：NPij表示新的相位频谱；NMij为新的幅度频谱.

得到NPij和NMij后， 根据图2可知， 利用逆向DFT， 得到初始密文. 逆向DFT模型如下：

依据模型(10)～(12)， 最终得到的初始密文见图5(c).

1.2 像素替代单元

对比图4(b)与5(d)可知， 经过混沌相-幅度变换后生成的密文， 其冗余性较低， 像素分布不均， 使其鲁棒性不佳. 对此， 本文设计了像素替代模型， 在时域上完成加密， 彻底改变像素值， 以提高密文安全性. 依据密钥Ⅱ XLogistic=X0， 迭代Logistic映射， 得到序列{X1， X2， X3， …， XM×N}：

其中:Xi代表模型(13)的状态参数. 并对{X1，X2，X3， …，XM×N}进行取整运算， 得到新的数组{Y1，Y2，Y3， …，YM×N}. 根据{Y1，Y2，Y3， …，YM×N}与步骤(1)得到的初始密文像素值， 设计像素替代模型：

其中：EP2代表输出密文； (EP1)ij为初始密文像素值.

经过模型(14)扰乱后， 得到的输出密文及其直方图分别见图6(a)与图6(b). 从图6可知， 经过像素替代单元扰乱后， 其像素分布较均匀， 拥有较为理想的伪随机特性.

图6 像素替代后的密文及其直方图分布

算法的整体描述：

① 设置一个256bit外部密钥， 根据模型(1)将其分割为8个子密钥；

② 根据模型(2)与模型(3)， 获取Logistic、Tent映射的初始条件值；

③ 利用2D离散傅里叶变换与模型(4)， 将图像转变为相与幅度成分；

④ 基于模型(8)与模型(11)， 生成初始密文；

⑤ 利用像素替代模型(14)， 改变初始密文的像素值， 输出最终密文.

2 仿真实验与分析

利用Matlab软件验证双域加密算法的合理性. 为了体现该技术的优异性， 设置对照组： 依据文献[9]的频域加密和依据文献[10]的时域加密， 分别记为A、B算法. 加密密钥为“a1, 02, 51,rw,hw, 79,pl, 64,cb, 6d, 1s,tk,xc,bn,pr,zq,zf,dv,of,k9,g7, 43,bj, 77,sc, 0a,m9, 82, 56,it, 94,xy”.

2.1 加密质量对比分析

以图7(a)为测试样本， 利用双域加密技术与对照组方案对其完成像素扰乱， 结果见图7(b)～(d). 依据图中内容， 三种算法在人眼视觉上无明显差别， 都无信息外漏.

图7 不同加密算法的密文质量

为了充分体现这三种加密算法的安全性， 引入信息熵模型来衡量[11]：

其中: Si代表图像像素； N∈[0, 256]为图像灰度值； P(Si)为Si出现的概率.

利用模型(15)， 计算图7(b)～(d)的信息熵值. 每次重复计算30次， 以获得密文信息熵的均值与最大值. 计算结果见表1. 根据表中数据显示， 双域加密算机制输出的密文的信息熵值最高， 其均熵与最大熵值为7.997 4和7.999 1； 而文献[9]和文献[10]对应的平均信息熵分别为7.993 2和7.994 6. 主要是双域加密算法在图像的频域与时域上同步加密， 继而提高了密文的安全性； 而对照组算法则是单域加密， 算法安全性不佳.

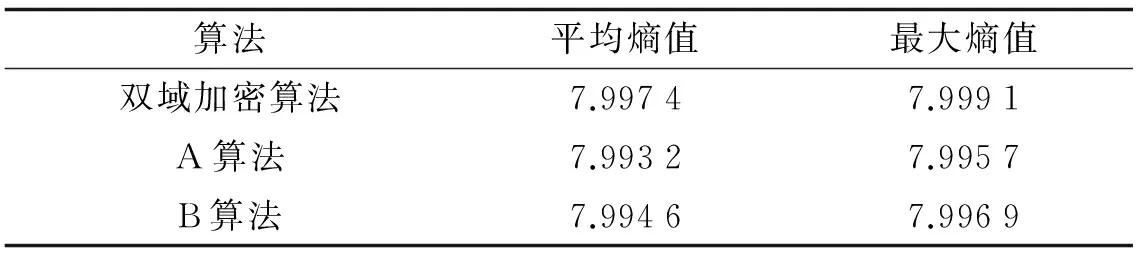
表1 不同加密算法的熵值

2.2 相邻像素的自相关特性

理想的加密算法能够显著消除两个相邻像素点的强烈自相关性， 在明文与密文中任意选择2 000对相邻像素点， 其Rxy模型[12]如下：

图8显示的是随机选取初始图像与输出密文中的两相邻像素点在水平线上的自相关特性结果. 由图8(a)可知， 初始图像的Rxy值较大， 约为0.973 3； 而经混沌相-幅度变换与像素替代后， 显著降低了Rxy值， 为0.002 4.

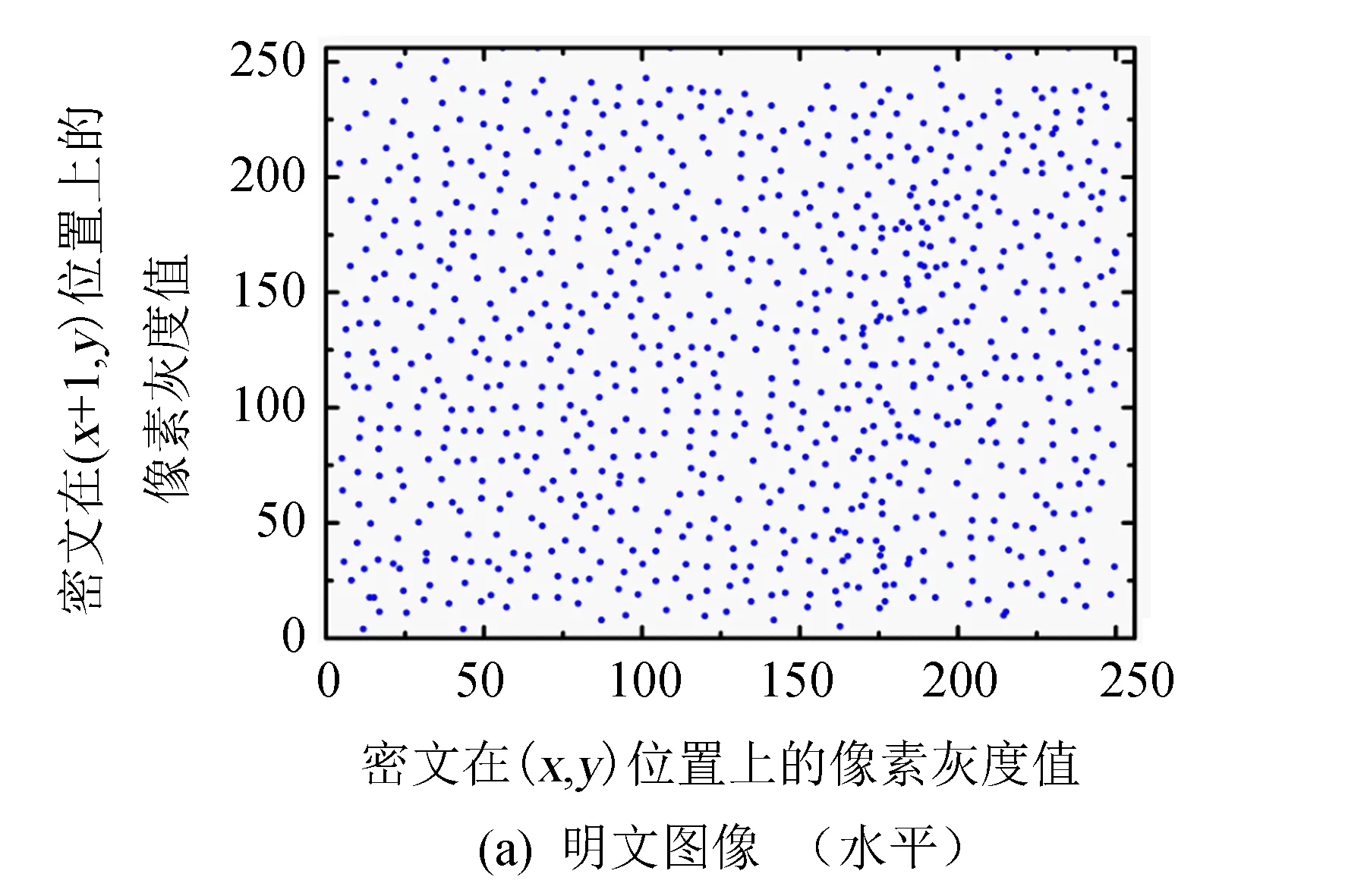
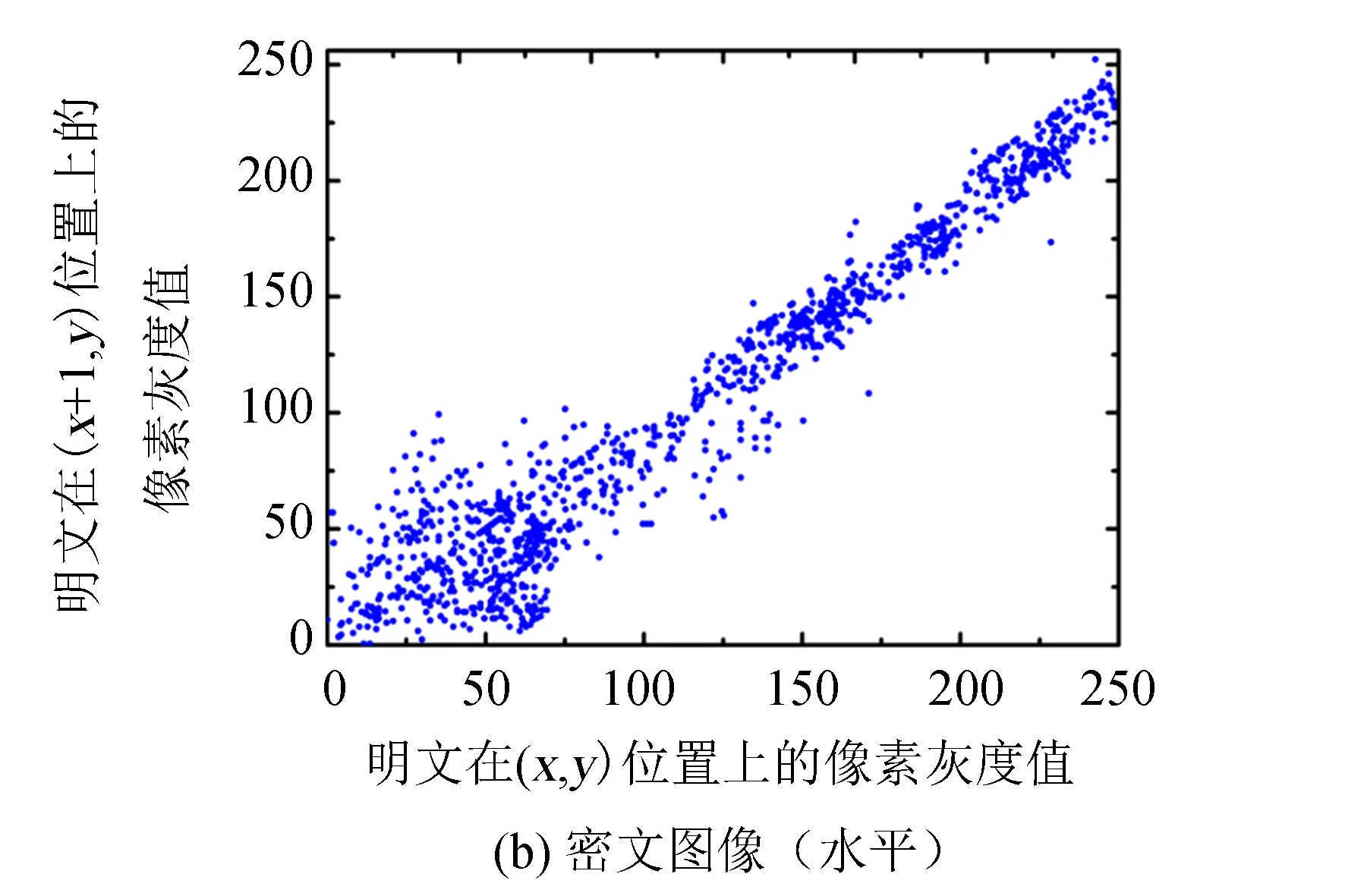
图8 自相关特性测试

参照文献[13]中的图像加密算法， 通过实验验证, 可以从水平相关系数等方面来对比这两种算法的安全性差异(见图9). 以图9(a)为目标， 利用这两种算法对其完成加密， 并测试这两种算法的的水平、 垂直、 对角线的相关系数. 依图可知， 经过双域加密， 安全性都很好， 无视觉泄露， 见图9(b)与图9(c).

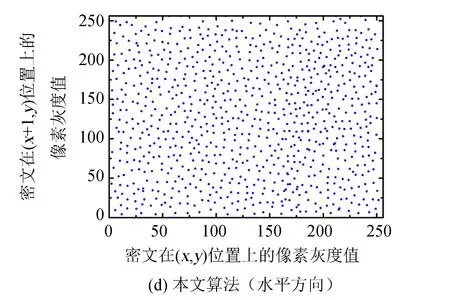
图9 不同算法在水平方向上的相关系数测试结果

另外， 从图9(d)与9(e)可知， 同为双域加密算法， 均能改变像素分布， 呈现较为均匀的分布形态. 但是由于文献[13]加密算法是先在频域分块加密， 然后在其结果上完成时域加密， 使其呈现像素空洞分布， 见图9(e)中的圆圈. 得到的相关系数分别为0.962 7、 0.954 8， 相比而言， 本文加密算法在安全改进上更为完善一些. 对角线与垂直方向的相关系数见表2. 依据这些数据， 可知两种算法的安全性比较接近， 都是用双域加密算法， 其加密图像都具有较高的抗攻击性.

表2 对角线与垂直方向的相关系数

2.3 解密效果对比分析

为了进一步体现算法的安全性， 仅改变初始密钥中的一个字符， 变为 “a1, 22, 51, rw, hw, 79, pl, 64, cb, 6d, 1s, tk, xc, bn, pr, zq, zf, dv, of, k9, g7, 43, bj, 77, sc, 0a, m9, 82, 56, it, 94, xy”. 利用该错误密钥与初始正确密钥对图7(b)进行还原， 结果见图10. 从图中可知， 本文双域加密算法的敏感性非常高， 即使改变其中一个字符， 都无法得到初始图像， 见图10(a). 只有正确的密钥才能获取其初始图像， 见图10(b).

图10 算法解密效果分析

2.4 加密算法效率

表3 各算法的加密效率

优异的加密算法应同时具备良好的加密效率与较高的安全性[4]. 为了体现算法的加密效率， 将本文双域加密算法与单域加密技术[9-10]以及双域加密算法[13]相比较 . 测试环境是DELL2.0 GHz、 双核CPU、 8 GB内存与Windows XP系统. 测试目标为512×512图像. 四种算法的计算代价见表3. 从表3可知， 本文双域加密算法因使用了一维混沌映射， 且同步完成图像在时域与空域加密， 使该算法避免了复杂的混沌系统与操作， 其时耗为0.28 s； 而文献[9]与文献[10]虽然是单域加密技术， 但是这两种算法使用了复杂的高维混沌系统， 增加了其算法的复杂度； 而文献[13]不但使用了高维混沌系统， 而且其空域与时域独立， 非同步加密， 使其算法的时耗比较大， 约为0.92 s.

3 结语

为了改善当前单域加密算法的安全性， 设计了混沌相幅变换算子耦合像素替代的双域图像加密算法. 引入离散傅里叶变换与Tent映射， 构造混沌相幅度变换单元， 完成图像的频域加密， 得到初始密文； 由迭代Logistic映射， 设计像素替代模型， 改变置乱图像的像素值， 在时域与频域内同步完成加密. 仿真结果显示： 与当前单域加密算法相比， 本文双域加密算法具有更强的密钥敏感性， 从而显著增强了算法的鲁棒性.

[1] Wang X Y, Xu D H. A novel image encryption scheme based on Brownian motion and PWLCM chaotic system[J]. Nonlinear Dynamics, 2014, 75(1): 345-353.

[2] Zhu C X, Liao C L, Deng X H. Breaking and improving an image encryption scheme based on total shuffling scheme[J]. Nonlinear Dynamics, 2013, 71(1): 25-34.

[3] Houcemeddine H, Rhouma R, Safya B. Improvement of an image encryption algorithm based on hyper-chaos[J]. Telecommunication Systems, 2013, 52(2): 539-549.

[4] 孙力, 黄正谦, 傅为民. 时间延迟与超混沌Chen系统相融合的图像加密算法研究[J].科学技术与工程, 2013, 13(35): 10 523-10 530.

[5] Himan K, Mohammad E. Image encryption using random bit sequence based on chaotic maps[J]. Arabian Journal for Science and Engineering, 2014, 39(2): 1 039-1 047.

[6] Ashutosh, Sharma D. Robust technique for image encryption and decryption using discrete fractional Fourier transform with random phase masking[J]. Procedia Technology, 2013, 10(12): 707-714.

[7] 肖迪, 谢沂均. 一种结合JPEG压缩编码的彩色图像加密算法[J]. 物理学报, 2013， 62(4): 2 405-2 408.

[8] 周琳, 杜广朝, 邵明省. 基于双随机编码正交映射的全息图像加密[J]. 电视技术， 2013, 37(1): 24-27.

[9] 王鹏, 袁操今, 王林, 等. 基于分数傅里叶变换的双彩色图像加密[J]. 激光技术, 2014, 38 (4): 551-555

[10] Zhang X P, Zhao Z M. Chaos-based image encryption with total shuffling and bidirectional diffusion[J]. Nonlinear Dynamics, 2014, 75 (2): 319-330

[11] Cao Z J, Ge Y C, Feng J L. Fast target detection method for high-resolution SAR images based on variance weighted information entropy[J]. Eurasip Journal on Advances in Signal Processing, 2014, 19(1): 1-11.

[12] Wang X Y, Luan D P. A novel image encryption algorithm using chaos and reversible cellular automata[J]. Communications in Nonlinear Science and Numerical, 2013, 18(11): 3 075-3 085.

[13] 王靖雯. 基于混沌理论的数字图像加密算法研究[D]. 哈尔滨： 哈尔滨理工大学, 2012: 14-33.

(责任编辑： 洪江星)

Image encryption algorithm based on chaos phase-amplitude transformation operator coupling pixel substitution

QIAO Lilong1， YANG Zhimin2

(1. Engineering Technology Institute, Shandong Vocational College of Foreign Affairs Translation， Weihai,Shandong 264504, China; 2. Department of Computer Science, Shandong University, Weihai, Shandong 264209, China)

In order to effectively prevent the image information from being stolen during the image was transmitting in the open network environment, the image encryption algorithm based on chaos phase-magnitude transformation operator coupling pixel substitution was proposed in this paper. Firstly, the permutation image was obtained by introducing the discrete Fourier transformation to covert the image into phase and amplitude components, as well as iterating the Tent map to generate phase and amplitude transformation operators. Then the pixel substitution was designed by Logistic map to change the pixel value of permutation image to synchronization encryption image in time domain and frequency domain. Simulation results showed that this algorithm had high security to effectively resist the plaintext attack and comparison with current image encryption, this algorithm had higher encryption efficiency.

image encryption; discrete Fourier transformation; external key; amplitude transformation; pixel substitution

2015-08-04

杨志敏(1952-)， 教授， 主要从事网络安全技术、 人工智能与CSCW应用技术研究, yangzhimin@sdu.edu.cn

山东省科技攻关资助项目(2009GG10004012)

10.7631/issn.1000-2243.2015.06.0759

1000-2243(2015)06-0759-08

TP391

A