一种新的叠加系统旋转效应的评估指标

韦铁平, 杨晓翔, 姚进辉, 许 航

(1. 福建工程学院机械与汽车工程学院， 福建 福州 350118；2. 福州大学机械工程及自动化学院， 福建 福州 350116；3. 福建省计量科学研究院， 福建 福州 350003)

一种新的叠加系统旋转效应的评估指标

韦铁平1, 2, 杨晓翔2, 姚进辉3, 许 航3

(1. 福建工程学院机械与汽车工程学院， 福建 福州 350118；2. 福州大学机械工程及自动化学院， 福建 福州 350116；3. 福建省计量科学研究院， 福建 福州 350003)

针对旋转效应是叠加系统测量不确定度的重要影响因素， 提出一种旋转效应的评估指标——力传感器所受的水平附加侧向力的波动量(Fm). 基于有限元法， 建立了叠加系统旋转效应的测量模型， 模拟结果显示增大均力板厚度有利于削弱Fm. 通过试验验证， 发现Fm越小， 旋转效应也越小. 在试验力级250 kN处， 均力板厚度为6、 9和12 mm的叠加系统测量的最大偏差值分别为0.000 59、 0.000 49和 0.000 28 mV/V. 有限元模拟和试验结果验证了评估指标的可行性， 同时也为叠加系统的结构优化提供了有效的手段.

叠加系统; 评估指标; 旋转效应； 附加侧向力； 有限元法

0 引言

目前， 国内外大型衡器的现场检定仍采用砝码作为标准力源. 利用砝码进行大型衡器检定存在着工作量多、 劳动强度大和运输成本高等一系列问题. 新研制的校准系统能实现大型衡器的无砝码现场检定[1]. 内部结构为叠加系统的高精度负荷传感器是该系统的核心部件之一， 它的测量准确度直接影响到整个校准系统的测量结果. 在检测过程中， 负荷传感器的放置具有非固定式和随意性等特点[2]， 控制好旋转效应对于提高测量准确度具有重要的意义.

在力基(标)准机(或材料试验机)对测力仪(或试件)施加轴向负荷时， 由于机器的结构缺陷(如不对称性)和不正常工作状态， 测力仪(或试件)的安装位置的偏心与倾斜以及机器和测力仪(或试件)之间的交互作用等原因将引起附加侧向力和力矩， 即寄生分量. 在寄生分量的作用下， 测力仪结构本身的不对称性(包括机械和电性能)使得测力仪在不同的方位上示值发生改变， 从而引起旋转效应[3].

旋转效应是力传感器等级评判的一个重要指标参数[4]， 其产生原因十分复杂. Nile研究了新开发的仪器设备与小力值传感器之间的交互作用(旋转效应)， 发现补偿平台的弯矩刚度不足会导致较大的旋转效应[5-6]. 通过大量的试验比对认证发现， 附加弯矩及力的非轴向分量是产生旋转效应的直接原因[7-8]. 归根结底， 传感器结构(包括机械结构和电性能结构)的不对称性和力标准机材料的不均匀性是引起旋转效应的根本原因[4]. 基于上述分析， 提出了许多旋转效应的改进措施. 最大限度地减小分压板的挠度能抑制叠加系统的旋转效应[9-10]； 改善传感器结构的对称性有利于改进旋转效应[11-12]； 通过力传感器的弯矩补偿可有效抑制由平行度引起的旋转效应[13]. 为了定量分析旋转效应在测量不确定度中的贡献， 许多学者提出了一系列的评估方法. 其中， A Bray[4]和C Xu[14]分别建立了试验力级与输出示值之间的数学关系， 并采用正弦函数来表示旋转效应； C Ferrero 采用六分量测力仪测量测力仪与力标准机之间的交互作用分量来评估旋转效应[8, 15]； Y K Park等人通过测量叠加系统中3个力传感器信号之间的差异来评估旋转效应[16]. 这些评估方法对于测力叠加系统的设计仍停留在试验阶段进行指导， 均未能在叠加系统试验之前对其旋转效应的大小做出评估和预测.

姚进辉[17]提出一种均力结构能使叠加系统的旋转效应大幅度改进. 韦铁平和杨晓翔等[18]对该均力结构进行模拟分析， 认为力传感器端面所受的水平附加侧向力的变化与旋转效应有着密切关系. 本文基于文献[17-18]， 提出了评估叠加系统旋转效应的指标Fm. 基于有限元法， 研究了叠加系统均力板的弯矩刚度与Fm的关系， 并通过试验验证了评估指标的可行性， 从而为叠加系统的设计提供简便有效的评估指标， 大大缩短了设计周期及成本.

1 叠加系统旋转效应评估指标的提出

1.1 均力结构的受力分析

图1 新型叠加系统的结构示意图

新型叠加系统的量程为300 kN， 由量程为100 kN、 性能与结构完全相同的三个柱式负荷传感器呈120°阵列分布组成， 结构如图1所示. 与传统叠加系统的结构相比， 新型叠加系统增加了均力结构(推力关节轴承组、 均力板和对中调节压头). 负荷传感器的加载端面为平面， 与端面为球面的对中调节压头对中接触. 负荷传感器通过定位销精确地固定在底座上. 作用在承压板上的载荷通过均力结构将尽可能均匀地分布在3个力传感器端面上.

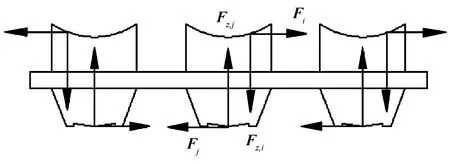
图2 旋转效应测量过程均力结构的受力分析

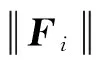
通过对中调节压头的试验力级最终传递至柱式负荷传感器的端面上. 根据牛顿第三定律， 作用在柱式负荷传感器端面上的水平附加侧向力Fk(k=1, 2, 3)与经过对中调节压头的作用力等大、 反向且作用线重合.

1.2 评估指标-侧向力波动量

基于三阶插值多项式模型， 建立力传感器试验力级与仪表输出示值之间的关系. 考虑到旋转效应， 在数学模型中引入正弦函数[14]：

式中：Xij为仪表输出的示值；fj为第j个试验力级；b(fj)为由不同方位测量产生的示值波动的正弦曲线的振幅， 与试验力级成正比；φij为力传感器在力标准机中的初始方位角；αi为旋转测量的第i个方位角；eij为由端部效应产生的随机示值；a0，a1，a2，a3为插值多项式的系数.

正弦函数项代表不同方位上的测量值引起的示值波动. 旋转不确定度计算公式[19]为：

由上式知， 旋转不确定度的大小与示值波动正弦曲线的振幅成正比， 即与试验力级成正比. 试验力级越大， 旋转效应的不确定度贡献越大. 为了改进传感器测量的不确定， 必须对旋转效应加以控制. 基于YKPark等人的研究[16]， 从另外一个角度考察旋转效应， 选择作用在柱式负荷传感器端面上的水平附加侧向力作为研究对象.

叠加系统的输出示值由并列的3个力传感器叠加而成. 由于叠加系统结构为非完全轴对称的， 力的传递过程将随着测量方位的改变而变化. 因此， 叠加系统不同方位的测量必然引起作用在力传感器端面上的水平附加侧向力发生改变. 根据力传感器在叠加系统中的排布及静力学理论分析， 理想的叠加系统结构在不同方位上的测量过程中， 3个力传感器的端面受力变化规律一致， 相位依次相差120°. 故仅需考察任一力传感器端面所受的水平附加侧向力的变化规律与叠加系统旋转效应的关系. 因此， 提出了叠加系统在同一力级作用下， 任一力传感器端面所受的水平附加侧向力的数学表达式：

式中：Fi为力传感器在第i个方位角时端面上所受的水平附加侧向力；F0为力传感器端面上所受的水平附加侧向力在各个方位上的平均值；A为力传感器端面上所受的水平附加侧向力正弦曲线的振幅；θ0为叠加系统在力标准机底座上的初始方位角；θi为第i个方位角.

由式(3)可知， 叠加系统旋转效应测量中， 力传感器端面水平附加侧向力的最大波动量为Fm=2A，Fm与侧向力的振幅A成正比.Fm与叠加系统旋转效应之间的关系将通过不同厚度均力板的叠加系统的旋转效应测量的有限元模型及相应的试验验证.

2 有限元模拟分析

2.1 旋转效应检测的有限元模型

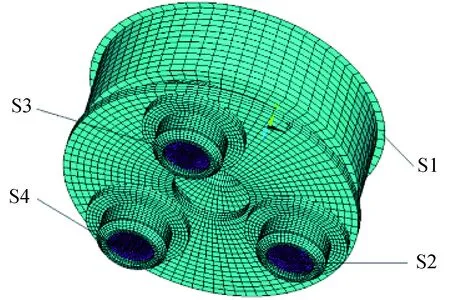
图3 简化的叠加系统旋转效应测量的有限元模型

为了研究均力板的厚度对叠加系统旋转效应的影响规律， 旋转效应测量的有限元模型将作如下假设及简化： 试验机与叠加系统交互作用的接触面假定为刚性， 由S1代替； 叠加系统与试验机的交互作用通过引入倾斜角为1°的试验力级来实现； 与对中调节压头相接触的3个力传感器由S2、S3和S4刚性面代替. 测量过程中， 刚性面S2、S3和S4全约束固定并通过提取其水平分力合成水平附加侧向力. 推力关节轴承内、 外圈为面—面接触， 摩擦系数取0.01； 对中调节压头球面与力传感器端平面为点—面接触. 简化的叠加系统旋转效应测量的有限元模型如图3所示.

叠加系统的旋转效应测量选择20， 60， 100， 150， 200， 250和300kN7个试验力级. 有限元模拟旋转效应的测量选择均匀的6个方位角(0°， 60°， 120°， 180°， 240°和300°). 在0°方位依次对7个力级进行测量， 结束后， 将叠加系统绕其轴线旋转60°至下一个方位上测量， 以此类推.

2.2 数值模拟结果

图4是均力板厚度为6， 9和12mm时， 在300kN力级作用下力传感器所受的水平附加侧向力的变化曲线. 图中显示， 每组叠加系统中3个力传感器变化曲线均为正弦曲线， 初始相位依次相差120°且Fm基本相等， 这与力传感器在叠加系统中的排布情况相一致. 模拟数据显示，Fm随着均力板厚度的增加而减小.

由此可知， 增大均力板弯矩刚度可削弱水平附加侧向力， 将使力值通过均力结构后更加均匀地分布在3个柱式力传感器上， 均力结构的均力效果更好.

图5显示， 力传感器水平侧向力的平均值及Fm与试验力级有关. 从图中可知， 力传感器所受侧向力的平均值与试验力级成线性关系. 而Fm与试验力级为非线性关系.Fm除了受到试验力级的影响， 还与均力结构有关. 由Fm变化曲线知， 随着试验力级增大， 均力结构的均力效果有变差的趋势.

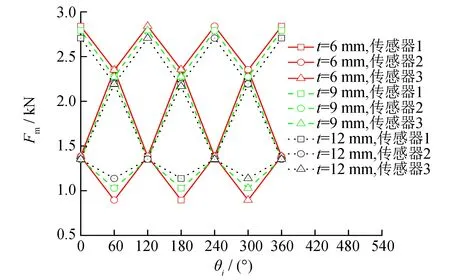
图4 均力板厚度对水平附加侧向力的影响规律

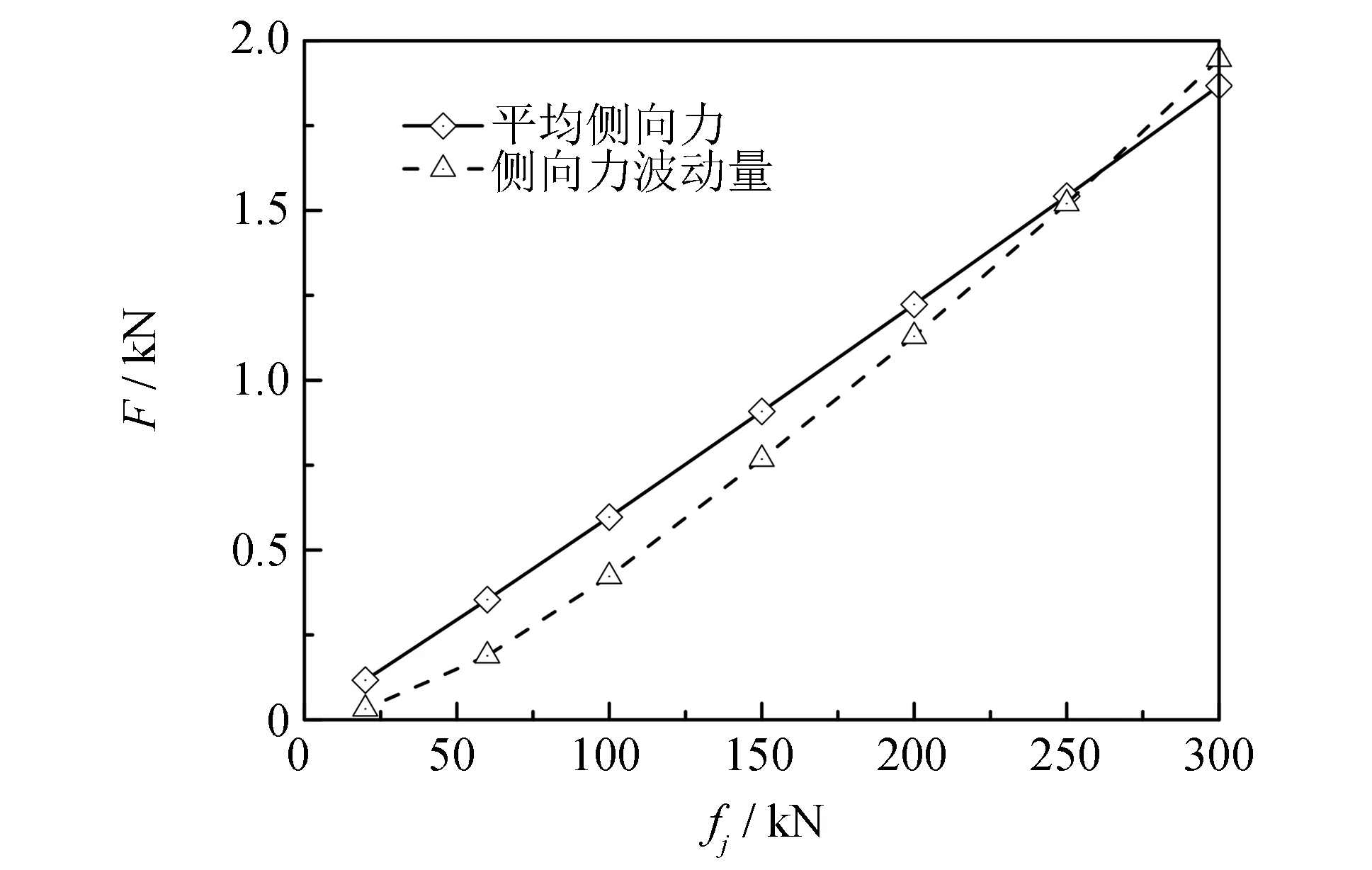
图5 侧向力随着力级改变的变化曲线

3 试验验证

为了验证旋转效应评估的指标及有限元模拟， 均力板厚度的选取与模拟参数一致， 分别为6、 9和12 mm. 3块均力板与叠加系统底座配套加工， 加工精度一致， 且均力板上平面与叠加系统底座的平行度均控制在0.02 mm/m以内. 3组叠加系统除了均力板厚度不同外， 其他部件完全相同， 以确保均力板厚度对旋转效应的影响的可比性.

试验机选择额定量程为300 kN的静重机， 最大相对偏差约为±5×10-5. 根据ISO 376: 2004(E) 测力仪校准规范， 选用0， 20， 60， 100， 150和250 kN六个试验力级. 在0°方位对6个试验力级测量结束后， 绕着叠加系统主轴线， 将其依次旋转至120°和240°进行同样的测量.

图6为3组叠加系统旋转效应的变化规律曲线. 从图中可知， 叠加系统的旋转效应总体上随着试验力级的增大而减小. 均力板的厚度越大， 叠加系统的旋转效应越小. 试验力级在小于60 kN(20%额定试验力级)时， 旋转效应的变化趋势比较剧烈， 且变化较为复杂.

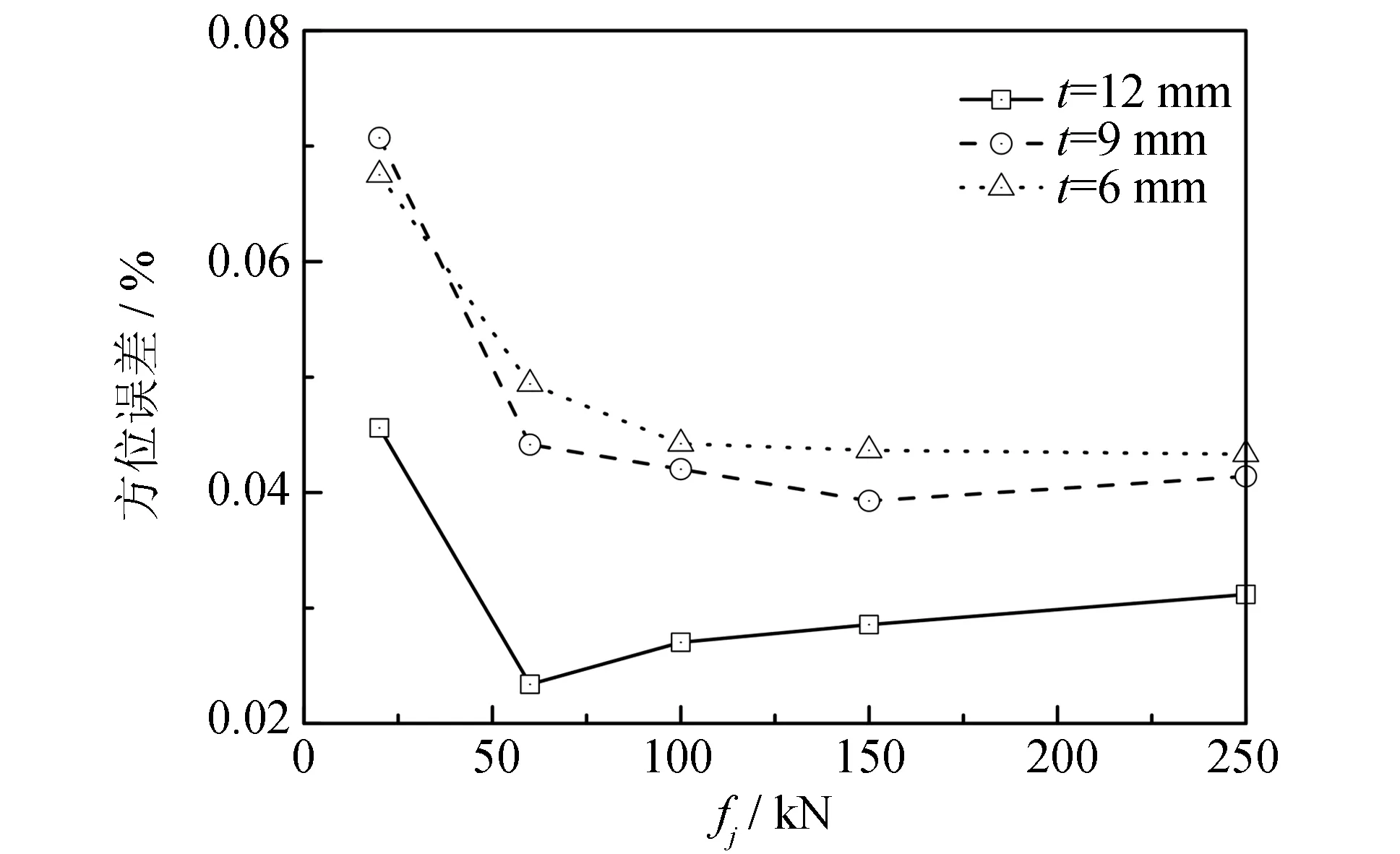
图6 均力板厚度对旋转效应的影响规律

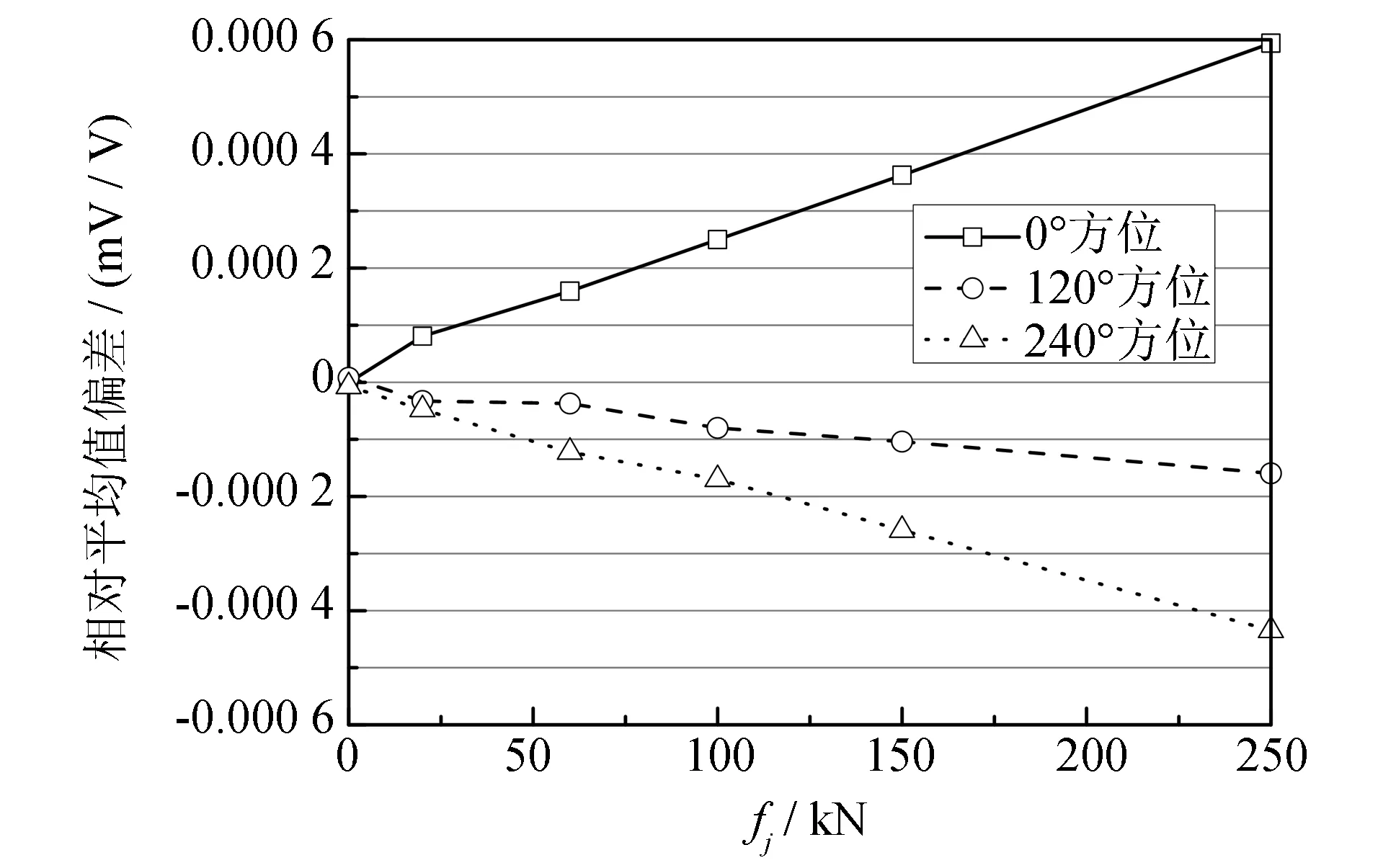
图7 t=6 mm时不同方位上的测量偏差值

由此可知， 均力板的厚度越大， 均力效果越好， 试验力级大于20%时尤为显著. 旋转效应的变化趋势验证了有限元模拟.

图7、 8和9分别为3组不同均力板厚度的叠加系统在不同方位上的测量偏差值ε(ε≈b(fj)). 由图可知， 总体上不同方位的偏差值ε随着试验力级的增大而加剧. 随着均力板厚度的增加， 各力级上的测量偏差值得到不同程度的抑制. 在最大试验力级250 kN处， 偏差值ε从均力板厚度为6 mm时的0.000 59 mV/V 降低到均力板厚度为12 mm时的0.000 28 mV/V.

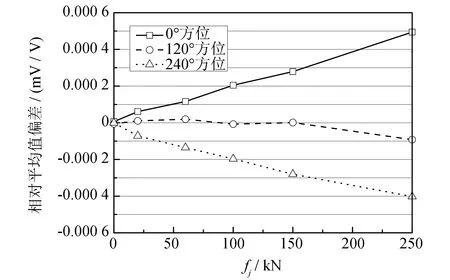
图8 t=9 mm时不同方位上的测量偏差值

图9 t=12 mm时不同方位上的测量偏差值

根据试验数据， 由公式(2)可知， 提高均力板弯矩刚度(厚度)有利于减小叠加系统的旋转不确定度.

综上所述， 增大均力板的弯矩刚度可以抑制叠加系统中力传感器水平附加侧向力Fm， 从而改善了叠加系统的旋转效应. 由于叠加系统与力标准机之间的交互作用十分复杂， 力值在叠加系统中的传递过程无法精确预测. 一方面， 有可能是有限元模型作了部分简化造成， 如叠加系统结构完全轴对称、 部件材料均匀无缺陷及力标准机利用刚性面代替等. 另一方面， 试验过程的操作精确性也会带来影响. 但这并不妨碍试验验证叠加系统旋转效应的评估指标的可行性及有限元模型的可靠性.

4 结语

提出一种新的叠加系统旋转效应的评估指标Fm. 通过有限元模拟与试验分析， 验证该评估指标的可行性. 分析结果表明， 增大均力板弯矩刚度有利于改进叠加系统的旋转效应； 力级越大， 旋转效应越小； 而旋转不确定度随着力级的增大而增大. 旋转效应的评估指标为叠加系统的结构优化提供了理论指导依据.

此外， 为了进一步分析均力板弯矩刚度对叠加系统旋转效应的影响， 接下来将对影响均力板弯矩刚度的其它因素(如均力板的弹性模量和惯性矩)作进一步的分析.

[1] 姚进辉. 采用非砝码检定大型固定式电子衡器的研究[J]. 中国计量, 2011(5): 88-90.

[2] 福建省计量科学研究院. 一种测力传感器结构: 中国, 201110449912.3[P]. 2011-12-29.

[3] 国家质量监督检验检疫总局. JJF 1011-2006力值与硬度计量术语及定义[M]. 北京: 中国计量出版社， 2007.

[4] Bray A, Barbato G, Franceschini F,etal. Rotational and end effects: a model for uncertainty evaluation in force measurements by means of dynamometers[J]. Measurement, 1996, 17(4): 279-286.

[5] Niehe S. A new force measuring facility for the range of 10 mN to 10 N[C]//Proc of the XVII IMEKO World Congress. Dubrovnik: [s.n.], 2003: 335-340.

[6] Niehe S. Force measuring facility from the range of 1 mN to 10 N[J]. Metrology Society of India, 2005, 20(3): 239-248.

[7] Peters M. Limits to the uncertainty achievable in force transfer[J]. Measurement, 1984, 2(4): 197-202.

[8] Ferrero C. The measurement of parasitic components in national force standard machines[J]. Measurement, 1990, 8(2): 66-76.

[9] Ferrero C, Marinari C, Martino E. Development and metrological characterization of a build-up force standard up to 3 MN[J]. System， 2003, 1(3): 6-9.

[10] Cruz J, Prdonoff V, Guerhard J. Research, development and characterization of a build-up system prototype up to 600 kN[C]//Proc of the IMEKO TC-3 Conf on Force, Mass, Torque and Pressure Measurements. Istanbul: [s.n.], 2001: 36-44.

[11] 倪守忠, 杜之平, 韩炜红. 板环式传感器的方位误差分析及校正方法[J]. 自动化仪表, 1999, 20(10): 30-31.

[12] Andrae J, Hons C, Sawla A. High precision force transducer with new method for online compensation of parasitic effects[J]. Measurement, 2003, 33(2): 173-178.

[13] Kang D I, Hong C S. Rotation effects of force transducers on the output of a build-up system[J]. Measurement, 1994, 14(2):147-156.

[14] Xu C. A practical model for uncertainty evaluation in force measurements[J]. Measurement Science and Technology, 1998, 9(11): 1 831-1 836.

[15] Ferrero C, Marinari C, Kumme R. Investigation of parasitic components in PTB’s 2 MN deadweight machine by using the INRIM six-component dynamometer[C]//Proc of the IMEKO XVIII World Congress on Metrology for a Sustainable Development. Rio de Janeiro: [s.n.], 2006, 17: 22.

[16] Park Y K, Kim M S, Kim J H,etal. A proposal for an evaluation method of force standard machines by using build-up system[C]//Proc of the IMEKO TC-3 Conf on Measurement of Force and Mass. Cairo: [s.n.], 2005: 1-5.

[17] 姚进辉. 组合式负荷传感器方位误差的减小[J]. 中国计量, 2013(3): 74-76.

[18] 韦铁平, 杨晓翔, 姚进辉, 等. 组合式负荷传感器旋转效应的研究[J]. 中国工程机械学报, 2014, 12(1): 67-72.

[19] BIPM IEC, IFCC ISO, IUP ACI. OIML(1995) Guide to the expression of uncertainty in measurement[M]. Geneva: ISO, 1995: 3.

(责任编辑： 沈芸)

A new evaluation index for the rotation effect of a build-up system

WEI Tieping1, 2, YANG Xiaoxiang2, YAO Jinhui3, XU Hang3

(1. College of Mechanical & Automotive Engineering, Fujian University of Technology, Fuzhou, Fujian 350118, Choina;2. College of Mechanical Engineering and Automation, Fuzhou University, Fuzhou, Fujian 350116, China；3. Fujian Province Institute of Metrology, Fuzhou, Fujian 350003, China)

The rotation effect is considered as an important factor for the measurement uncertainty of a build-up system. The largest difference (Fm) between the three additional side loads, which horizontally act on the three load cells in the build-up system, was defined as an evaluation index for the rotation effect. Measurement models of the build-up system were created based on the finite element method, and the results revealed thatFmwas reduced with the increase of the thickness of the balance structure. The rotation effect was restrained with the increasing ofFm, which was validated by the experimental results. Three deviations including 0.000 59, 0.000 49 and 0.000 28 mV/V were obtained at 250 kN, which were corresponded to three different thickness of the balance structure 6, 9 and 12 mm respectively. Effectiveness of the evaluation index was verified by the finite element simulations and the tests, which was helpful to improve the structure of the build-up system.

build-up system; evaluation index; rotation effect; additional side load; finite element method

2014-12-11

杨晓翔(1963-)， 教授， 博导， 主要从事计算力学及其工程应用研究， yangxx@fzu.edu.cn

国家重大科学仪器设备开发专项基金资助项目(2011YQ090009); 国家质检总局科技计划基金资助项目(2010QK017)

10.7631/issn.1000-2243.2015.06.0796

1000-2243(2015)06-0796-06

TH823; O343

A