高灵敏度SAW纱线张力传感器研究*

雷冰冰， 卢文科， 赵春锋

(东华大学 信息科学与技术学院，上海 201620)

高灵敏度SAW纱线张力传感器研究*

雷冰冰， 卢文科， 赵春锋

(东华大学 信息科学与技术学院，上海 201620)

灵敏度是声表面波(SAW)纱线张力传感器成功检测纱线张力的关键。通过对SAW纱线张力传感器的灵敏度和基片应变率之间关系的研究，提出了通过增加基片应变率来提高传感器灵敏度的理论。以该理论为指导，给出了通过灵活设计基片尺寸来获得最佳基片应变率的设计方案。为了得到最佳基片应变率对应的基片尺寸，建立了基片应变率和基片尺寸之间的数学模型，提出了求解最大基片应变率所对应基片尺寸的线性规划模型，即最佳灵敏度所对应基片尺寸。实验表明：该方法可以有效提高SAW纱线张力传感器的灵敏度，灵敏度达3 132.4 Hz/gf。

声表面波; 灵敏度； 纱线张力传感器； 基片应变率； 线性规划

0 引 言

声表面波(surface acoustic wave, SAW)传感器对其基片表面或者附近的物理、化学特性敏感[1,2]。对SAW传感器来说，外界的扰动会引起其传输媒质和波的传输特性的改变。目前，SAW传感器已广泛地应用于对物理量[3,4]、化学量[5～7]的检测。采用SAW传感器测量纱线张力具有高精度、高灵敏度、响应速度快等优点。其中，灵敏度作为衡量SAW纱线张力传感器的一个重要技术指标，是判定SAW纱线张力传感器检测纱线张力成功与否的关键。

为了提高SAW纱线张力传感器的灵敏度，本文分析改变SAW纱线张力传感器基片应变率对于灵敏度产生的影响，提出了基于ANSYS的高灵敏度SAW纱线张力传感器的设计方法。实验表明：该方法可以有效提高SAW纱线张力传感器的灵敏度。

1 传感器结构与原理

SAW纱线张力传感器结构示意图如图1所示，主要由金属底座、石英垫片、传感器基片、导纱环、吸声材料构成。点P为导纱环和传感器基片之间的粘接点，并且点P位于点X和点Z的正中。定义SAW纱线张力传感器基片长为L、宽为W，石英垫片长为Ls、宽为Ws，基片顶边到叉指换能器顶端的距离为dt，基片左边到叉指换能器最左端的距离为dl。

SAW纱线张力传感器使用42°Y-X石英基片，采用光刻法制成SAW延迟线型传感器，其工作频率为169.4 MHz。当纱线张力被施加在导纱环时，SAW纱线张力传感器基片将产生应变，这会引起SAW传播速度和叉指换能器波长的变化，进而改变SAW延迟线型传感器的输出频率，亦即可通过检测传感器输出频率变化来测量纱线张力的大小。若SAW纱线张力传感器的输出频率为f，则有

f=f0+Δf,

(1)

式中f0为在纱线张力为零时传感器的输出频率，Δf为纱线张力不为零时传感器输出频率的变化值。

图1 SAW纱线张力传感器结构图

2 传感器设计

2.1 传感器灵敏度和基片应变率之间的关系

SAW纱线张力传感器基片的应力—应变示意图如图2所示。在图2中，当纱线张力被施加在受力点P时，压电基片将产生应变，并且总有点Mx产生最大矢量位移，定义最大矢量位移为ΔL。由于ΔL/L的值总是小于0.2 %，所以,假定压电基片是沿长度方向被拉伸，且拉伸量为ΔL,于是，压电基片的应变可写为

(2)

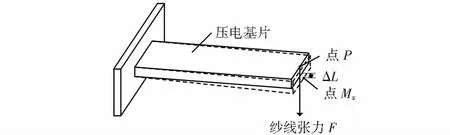
图2 压电基片应力—应变示意图

压电基片的应变会引起SAW传播速度和叉指换能器波长的变化，这样SAW纱线张力传感器输出频率和基片应变之间的函数关系可表示为[8]

(3)

式中k′为材料常数，λ0,v0分别为纱线张力为零时叉指换能器的波长、SAW传播速度。

联合式(1)和式(3)，可得

Δf=f-f0=f0ε(k′-1).

(4)

因为石英的应力—应变关系是线性关系，式(2)可变换为

(5)

式中 ΔL′为单位力所引起的基片矢量位移。

把式(5)代入式(4)，得

(6)

(7)

式中 α为SAW纱线张力传感器的灵敏度。

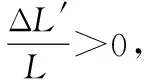
α=βε′,

(8)

式中β为常系数，ε′为单位力在单位长度基片上所能够引起的矢量位移，定义ε′为SAW纱线张力传感器的基片应变率。

由于f0>0，(k′-1)>0，可得β>0，所以,式(8)中参数α和参数ε是正相关的,即SAW纱线张力传感器的基片应变率越高，则其灵敏度就会越高。由此可见，可以通过增加SAW纱线张力传感器的基片应变率来实现SAW纱线张力传感器灵敏度的提高。研究发现，在基片厚度已定的情况下，SAW纱线张力传感器的基片应变率会随基片尺寸的改变而变化，如此，则可以通过改变基片尺寸来灵活设计传感器的灵敏度，并且得到具有最佳灵敏度的SAW纱线张力传感器。为了实现这一目标，需要建立基片应变率和基片尺寸之间的数学模型。

2.2 传感器基片应变率和基片尺寸之间的关系

改变传感器基片尺寸会引起传感器基片应变率的变化，所以，可以称参数L,W为解释变量，参数ε′为被解释变量。那么，根据被解释变量和解释变量之间的因果关系，使用多元线性回归分析方法，SAW纱线张力传感器基片应变率和基片尺寸之间的数学模型可表示为

ε′=k0+k1L+k2W+k3L2+k4LW+k5W2+k6L3+k7L2W+k8LW2+k9W3+e,

(9)

式中k0,…,k9为回归系数，e为随机误差。

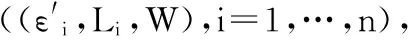
(10)

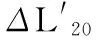
图3是长7mm、宽3mm的基片，在施加20gf纱线张力时基片应力—应变有限元仿真结果，可见基片产生最大矢量位移为0.001 992mm(1 992nm)，则该基片的应变率经计算为14.23×10-6。不同尺寸基片的应力—应变有限元仿真结果如表1。

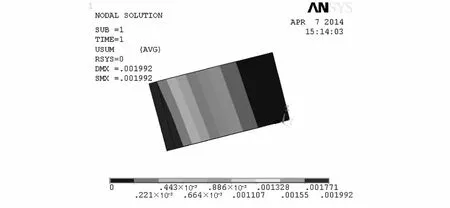
图3 基片应力—应变有限元模型仿真结果

表1 传感器基片应力—应变有限元模型仿真结果

基于表1中的数据样本，采用最小二乘法求解式(9)的回归系数，得k0=49.284 7,k1=1.301 7,k2=-33.883 7,k3=0.546 6,k4=-1.225 7,k5=8.135 2,k6=-0.001 8,k7=-0.068 3,k8=0.186 8,k9=-0.659 8。将回归系数代入式(9)，可以得到SAW纱线张力传感器基片应变率和基片尺寸之间的函数关系为

ε′=49.284 7+1.301 7L-33.883 7W+0.546 6L2- 1.225 7LW+8.135 2W2-0.001 8L3- 0.068 3L2W+0.186 8LW2-0.659 8W3.

(11)

在式(11)中，参数ε′的相关系数R2=0.999 3，其拟合曲面如图4所示。

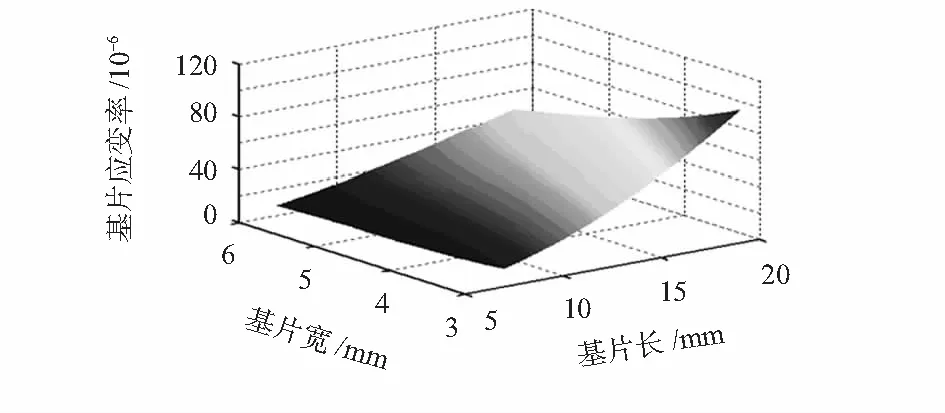
图4 传感器基片应变率与其尺寸的关系曲线

2.3 SAW纱线张力传感器最佳灵敏度的求解

SAW纱线张力传感器灵敏度是SAW纱线张力传感器基片应变率的单调增函数，所以,可以得到SAW纱线张力传感器的最佳灵敏度在传感器基片应变率取最大值时。根据式(11)可知，SAW纱线张力传感器基片应变率会随传感器基片尺寸变化而改变。那么，为了得到SAW纱线张力传感器的最大基片应变率，建立一个线性规划模型来达到这一目的。同时考虑SAW纱线张力传感器基片尺寸受限于实际应用环境和叉指换能器的尺寸，选取合适的约束条件,这一线性规划模型可以表示为

maxε′,

s.t. 7≤L≤19,3≤W≤6.

使用工具软件Lingo求解线性规划模型可得，在L=19 mm，W=3 mm时，基片应变率ε′取得最大值100.85×10-6，此时SAW纱线张力传感器的灵敏度可取得最大值。

3 实 验

制作基片长19 mm、宽3 mm的SAW纱线张力传感器S1来验证分析结果，传感器其它设计参数为Ls=3 mm,Ws=2.5 mm,dl=1.2 mm,dt=0.3 mm。传感器S1的测试结果如表2。根据式(6)，使用最小二乘法，可得传感器S1输出频率变化值和纱线张力之间的函数关系为

Δf=206.8+3132.4F.

(12)

在式(12)中，参数Δf的相关系数R2=0.999 9，其拟合曲线如图5所示。

表2 传感器S1测试结果

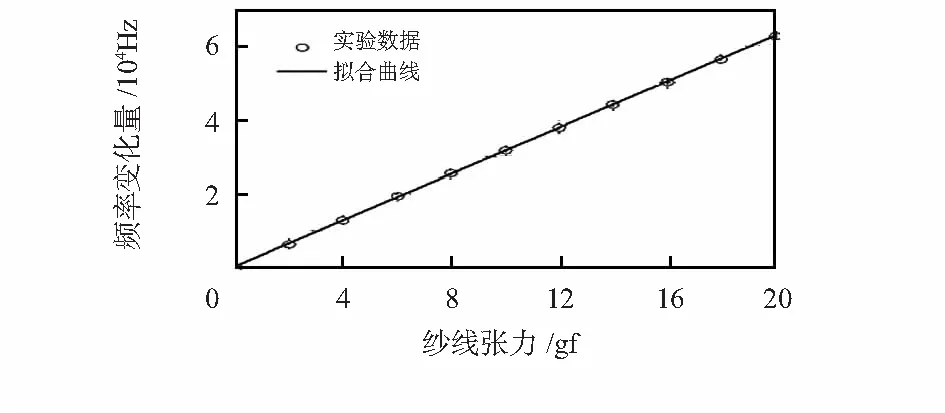
图5 传感器频率变化量与纱线张力的关系曲线

如式(12)所示，SAW纱线张力传感器S1的灵敏度可达3 132.4 Hz/gf。为了验证分析结果的正确性，随机制作尺寸区间范围内5个不同尺寸基片的传感器，它们的设计参数和灵敏度如表3，其中参数Ws,dl,dt同传感器S1。在表3，可以看到5个不同基片尺寸的传感器灵敏度均小于传感器S1的灵敏度，由此可知基于ANSYS的高灵敏度SAW纱线张力传感器设计方法是有效的。同时证明通过灵活设计SAW纱线张力传感器基片尺寸来提高SAW纱线张力传感器灵敏度的方法是可行的。

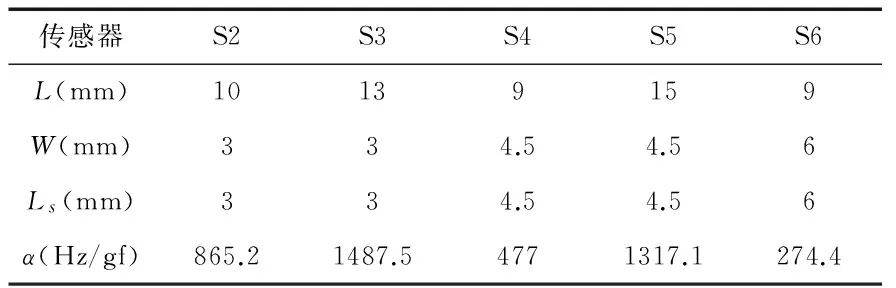
表3 传感器S2～S6设计参数和灵敏度

4 结 论

本文通过对SAW纱线张力传感器灵敏度和SAW纱线张力传感器基片应变率之间关系的研究，提出了通过增加基片应变率来提高传感器灵敏度的理论，即通过调整基片尺寸，使得传感器的压电基片取得最大应变率，此时对应基片尺寸的SAW纱线张力传感器能够获得最佳灵敏度。本方法基于有限元仿真软件ANSYS实现，能够有效提高SAW纱线张力传感器的灵敏度，也可用于其它基于悬臂梁结构SAW力敏传感器的设计中，并且高效、成本低廉。

[1] 李淑红，赵启大，廖同庆，等．基于声表面波技术探测微量气体的理论分析[J]．传感器与微系统，2008，27 (8)：63-65．

[2] Wen C B,Zhu C C,Ju Y F,et al.A novel dual track SAW gas sensor using three-IDT and two-MSC[J].IEEE Sensors Journal,2009,9(12):2010-2015.

[3] Singhn K J,Elmazria O,Sarry F,et al.Enhanced sensitivity of SAW-based pirani vacuum pressure sensor[J].IEEE Sensors Journal,2011,11(6):1458-1464.

[4] Ye X S,Fang L,Liang B,et al.Studies of a high-sensitive surface acoustic wave sensor for passive wireless blood pressure measurement[J].Sensors and Actuators A:Physical,2011,169(1):74-82.

[5] 向继文，陈依民，徐成志，等．声表面波NO2传感器敏感膜研究进展[J]．传感器与微系统，2012，31(9)：1-4．

[6] Marc B,Kai M,Johannes F,et al.A novel fabrication method of fiber-optical planar transmission sensors for monitoring pH in concrete structures[J].Sensors and Actuators B:Chemical,2008,131(2):504-508.

[7] Liu S,Sun H W,Nagarajan R,et al.Dynamic chemical vapor sensing with nanofibrous film-based surface acoustic wave sensor-s[J].Sensors and Actuators A:Physical,2011,167(1):8-13.

[8] 陈 明，范远东，李岁劳．声表面波传感器 [M]．西安：西北工业大学出版社，1997：29-31．

[9] Lu W K,Lu X Z,Zhu C C,et al.Solving three key problems of the SAW yarn tension sensor[J].IEEE Transactions on Electron Devices,2012,59(10):2853-2855.

Research on high-sensitivity SAW yarn tension sensor*

LEI Bing-bing, LU Wen-ke, ZHAO Chun-feng

(School of Information Science and Technology,Donghua University,Shanghai 201620,China)

Sensitivity is the key in process of successful detection on yarn tension using SAW yarn tension sensor.By studying relationship between sensitivity of SAW yarn tension sensor and substrate strain rate of SAW yarn tension sensor,propose a theory,which can improve sensor sensitivity through increasing substrate strain rate.Based on the theory,a scheme is given to obtain the optimal substrate strain rate through flexibly design substrate size.In order to obtain substrate size corresponding to the optimal substrate strain rate,mathematical model between substrate strain rate and substrate size is established;a linear programming model is proposed to solve the substrate size corresponding to the maximum substrate strain rate,that is the substrate size corresponding to the optimal sensitivity.Experimental results confirm that the method can significantly increase SAW yarn tension sensor sensitivity up to 3 132.4 Hz/gf.

SAW; sensitivity; yarn tension sensor; substrate strain rate; linear programming

10.13873/J.1000—9787(2015)04—0045—04

2014—08—21

国家自然科学基金资助项目(61274078)；教育部博士点基金资助项目(20120075110006)；上海市教育委员会科研创新项目(13ZZ049)；中央高校基本科研业务费专项资金资助项目(CUSF—DH—D—2014056)

TP 212

A

1000—9787(2015)04—0045—04

雷冰冰(1985-)，男，河南偃师人，博士研究生，研究方向为表面波器件、传感器。