改进粒子群算法应用于锅炉汽包水位控制
2015-05-11魏晋军
魏晋军,张 玮,刘 角,马 迪
(太原理工大学过程装备与控制工程系,太原 030024)
改进粒子群算法应用于锅炉汽包水位控制
魏晋军,张 玮,刘 角,马 迪
(太原理工大学过程装备与控制工程系,太原 030024)
为提高粒子群算法的收敛速度,根据粒子位置期望的数学分析,提出一种基于高斯分布的粒子群优化算法,该算法利用高斯分布随机数选取的特性,若选择合适的参数,不仅有利于算法收敛速度增快,而且增加了跳出局部最优的机制。应用于四个标准测试函数表明,当高斯分布选取μ=0.5,P=97%(σ2=0.23)时,性能较优秀。之后将改进的粒子群算法应用于锅炉汽包水位串级三冲量PID控制系统的参数整定当中,经过matlab中的simulink模块仿真,取得较好的效果。
粒子群优化算法;收敛速度;高斯分布;锅炉汽包水位
锅炉汽包水位是工业锅炉安全正常运行的一个非常重要的指标[1]。当水位过高时,会影响汽水分离,导致蒸汽带水进入过热器,并在过热管内结垢,从而轻则影响传热效率,重则导致传热管爆炸;若水位过低时,则会破坏部分水冷壁的水循环,引起水冷壁的局部过热而爆管。目前工业生产中常采用串级三冲量系统对其实施控制[2],在整定PID参数的过程中,主要的方法是依靠半经验公式算出粗略值,然后再具体调整,但是当生产状况发生变化时,参数整定就会变得复杂而困难。所以,寻求一种较好的整定方法,就成为当前重要的任务[3]。
1995年由Kennedy和Eberhart提出的粒子群优化(Particle Swarm Optimization,PSO)算法[4],是具有全局性、随机性的群智能优化算法。PSO算法的原理简单、控制参数少、操作方便,同时相比其他算法又有着启发性、多样性、全局寻优性和鲁棒性的优点。现在已经成功应用于求解各类型复杂优化问题,用于PID参数整定的例子也不少,但是如何应用于锅炉汽包水位这个复杂的、动态变化的系统仍然是一个难点。
1 锅炉汽包水位控制系统
汽包水位[5]是随着给水流量和蒸汽流量的变化改变的。汽包水位的动态特性方程[6]可以化简为:
(1)
UD=△D/Dmax,UW=△W/Dmax
(2)
其中,h为汽包水位的高度,T1、T2为时间常数,TW、TD分别是给水流量项和蒸汽流量项的时间常数,KW、KD分别是给水流量项和蒸汽流量项的放大倍数,W是锅炉给水流量,D是锅炉蒸汽流量。
汽包水位在给水流量作用下的传递函数为:
(3)
其中,K1表示汽包水位的飞升速度,Tα表示延迟时间,K1和Tα与锅炉结构有关。
令K=(KDT2-TD)/T1,T=T1/KD,则汽包水位在蒸汽流量作用下的传递函数为:
(4)
其中,1/T表示汽包水位对于蒸汽流量的飞升速度,T2表示“虚假水位现象”的延迟时间。
整个串级控制系统由两个闭合回路形成,一是在水位控制中起辅助作用的副回路,由给水流量测量装置、副调节器和给水调节阀构成,这个水流量回路可以消除给水侧的扰动,稳定给水流量;二是可以维持水位接近设定值的主回路,由水位变送器、主调节器、副回路以及被控对象所构成的回路,这个水位回路可以消除各种扰动对水位的影响。具体结构如下图所示:
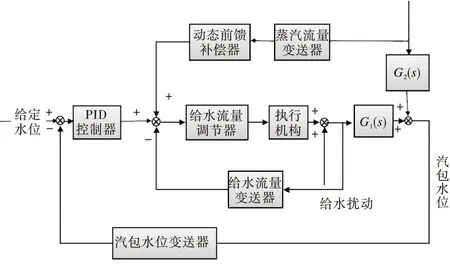
图1 三冲量PID控制系统结构Fig.1 Three-impulse PID control system structure
2 粒子群优化算法
粒子群优化算法的数学描述为:设搜索空间为D维,总粒子数为n,第i个粒子位置表示为向量Xi=(xi1,xi2,…,xiD),其飞行速度为Vi=(vi1,vi2,…,viD).第i个粒子迄今为止搜索到的其个体的最优位置为pbesti=(pi1,pi2,…,piD),整个粒子群迄今为止搜索到的全局的最优位置为gbest=(pg1,pg2,…,pgD),按追随当前最优粒子的原理,粒子Xi将按式(1)和式(2)改变速度和位置。
(5)
(6)
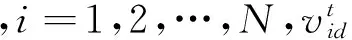
PSO算法作为一种仿生智能算法,其对目标函数的要求很低,有时甚至没有要求,算法的普适性强,是较为可靠和有效的全局优化算法之一。但是算法同样会出现后期收敛速度较慢,容易陷入局部最优等问题[7]。面对这种问题,本文提出了改进思路。
3 改进的粒子群优化算法
首先引入Jiang[8]等提出的PSO收敛定理。
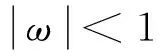
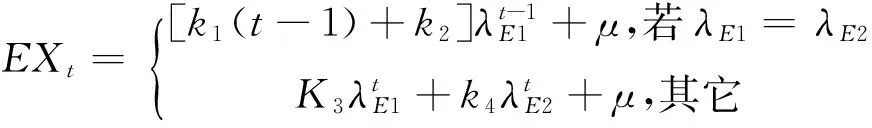
(7)
证明:已知PSO位置期望的迭代公式为:
(8)
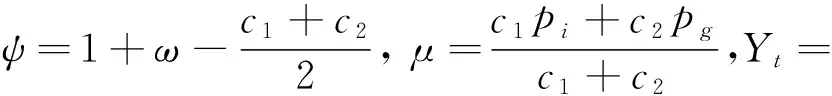
Xt-μ.
则有:
EYt-1-ψEXt+ωEYt-1=0
(9)
对应的特征方程为:
λ2-ψλ+ω=0
(10)
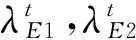
(11)
EXt=EYt+μ
(12)
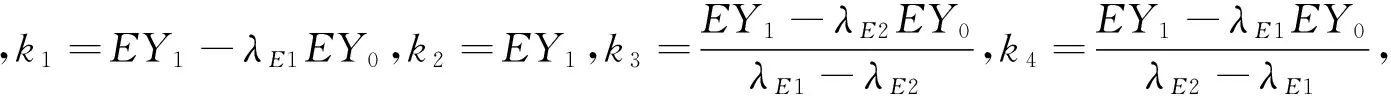
在定理1的证明中忽略了PSO算法中随机量的影响,而随机量是随机算法中非常重要的一部分,给算法带来创新性和多样性。现在大多文献中分析随机量的方法都是采用多次实验来得到结果,因为分析随机量的影响无法从数学公式中得到解答。但是通过概率学的基础知识可以知道:粒子的位置每次迭代,若取得的随机量不同,则会出现跟粒子的期望位置相比的一个“误差”,根据中心极限定理,将这个“误差”经过足够多次的卷积后,可以得出一个近似服从高斯分布的随机分布。
同时,在粒子群构建的模型中,用粒子群模拟鸟群群体觅食行为是体现群体智能的一种模拟。而事实上,对于某只鸟个体的行为,则不单单是群体智能一个因素影响,影响其运动轨迹的随机因素很多,而且每个因素的作用都不大,这样的情况也应该是高斯分布的使用范围。
所以,本文提出了用高斯分布取代原来PSO算法中的均匀分布,将公式(5)改进如下:
(13)
其中N1、N2表示高斯分布。
高斯分布的参数怎样设定才能取得较好的效果呢?高斯分布的参数有两个:期望μ和方差σ2.由于是改进算法,所以很多数据并不成熟,所以在尽量不改变原算法的基础上进行参数改进,这样可以保证有一定对比性。由于公式(5)中的(0,1)上均匀分布的期望是μ=0.5,因此本文把高斯分布的期望μ依此设定成0.5.这样也可以保证高斯分布的随机数在0~1之间取值的分布是对称的。其实,当μ取其他不为零的值(如μ=0.8)时,根据高斯分布自身的性质,相当于扩大或缩小了相应的c1,c2值,对于高斯分布本身的设定没有影响。图2是两种不同期望的高斯分布。
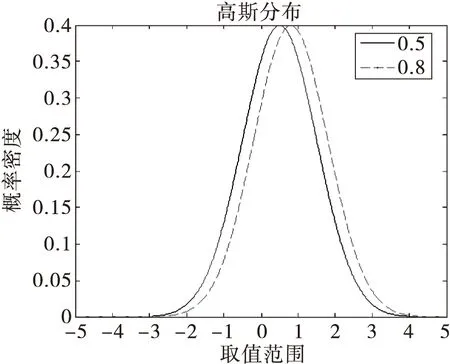
图2 高斯分布不同期望的图像对比Tab.2 Image contrast between different values at Gaussian distribution
而选取方差σ2时,需要考虑随机数在(0,1)之间出现的概率。因为当方差σ2较小时,随机数在0.5处集中趋势明显,失去随机算法中随机分布项的意义;若方差较大,则会影响算法的收敛性。而对于超出[0,1]区间的随机数,小于0的值,相当于粒子速度会朝着局部和全局最优相反的方向运动,而大于1的值,则会提高粒子朝着局部和全局最优位置的运动速度。本文所以选择用(0,1)之间的随机数取值的置信度来作为高斯分布的参数选择。并且置信度与方差之间也存在着联系,具体关系为:
(14)
当置信度取70和90的情况时如图3.
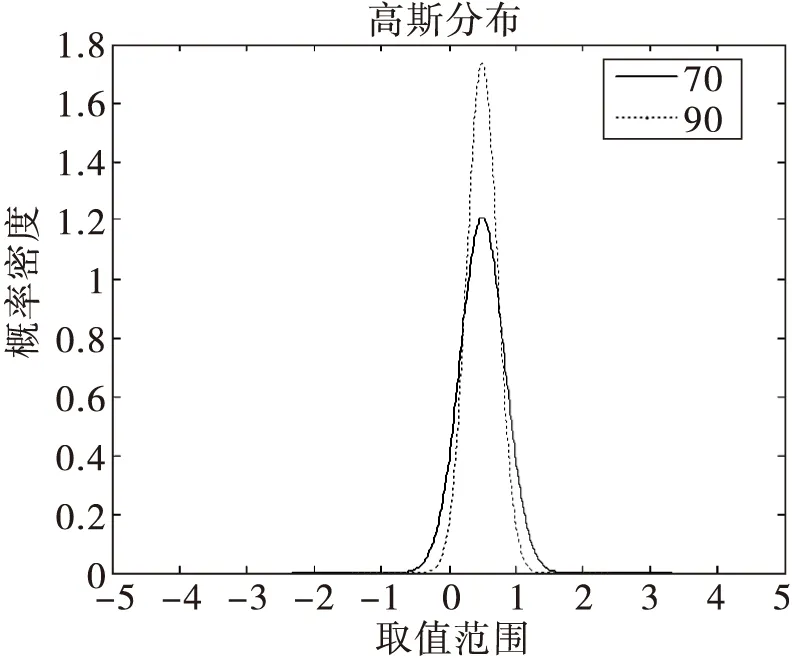
图3 高斯分布在[0,1]之间的置信度取70和90的图像对比Fig.3 Degree of confidence at Gaussian distribution values in[0,1]contrast between 70 and 90
用MATLAB进行仿真实验做比较结果,设定PSO参数ω=0.724,c1=1.468,c2=1.468,维数D为30,最大迭代次数为5 000,种群大小M为250.而高斯分布的期望μ=0.5,方差跟置信度的比值列表如下:
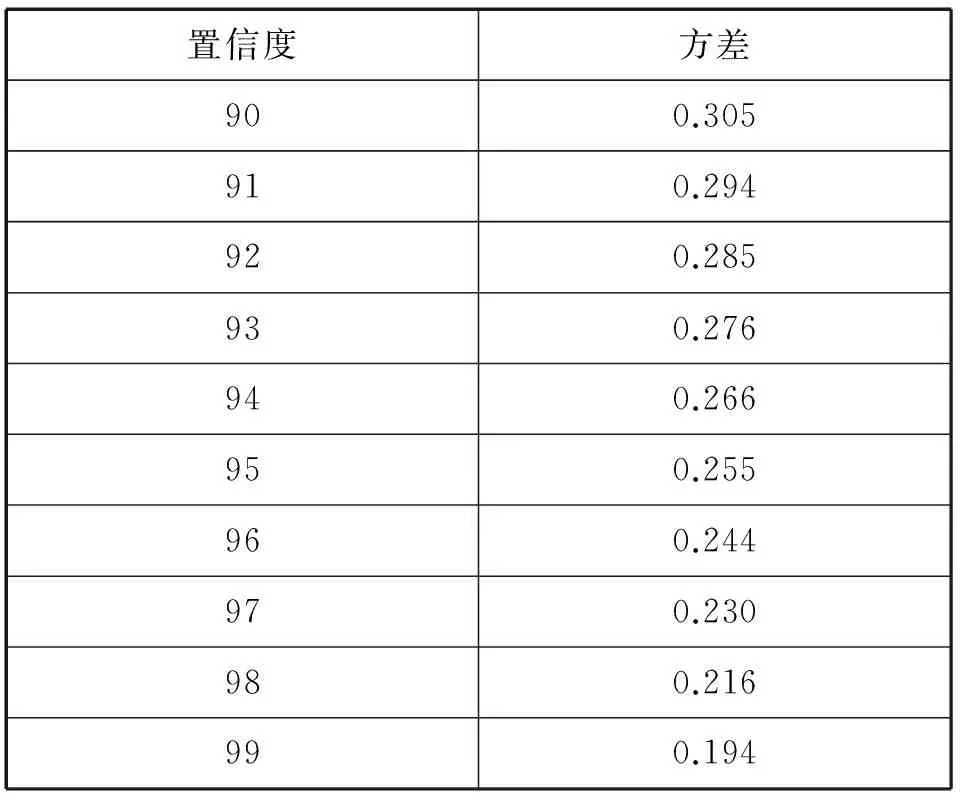
表1 置信度及对应的方差Tab.1 Confidence level and the corresponding variance
选取4个标准测试函数测试高斯分布不同置信度时的性能。
Sphere函数:

Rosenbrock函数:
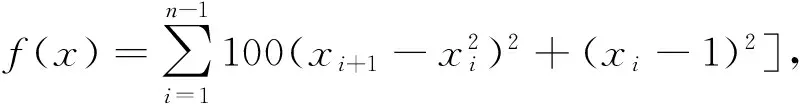
Rastrigin函数:
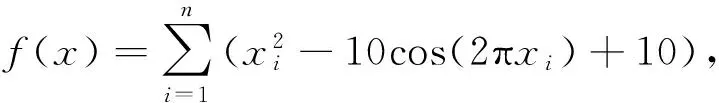
Griewank函数:
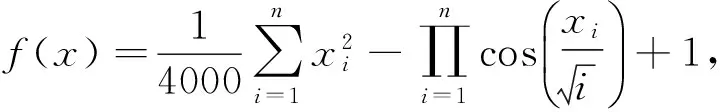
下面4个表是不同置信度分别对4个标准测试函数做30次仿真实验的结果。
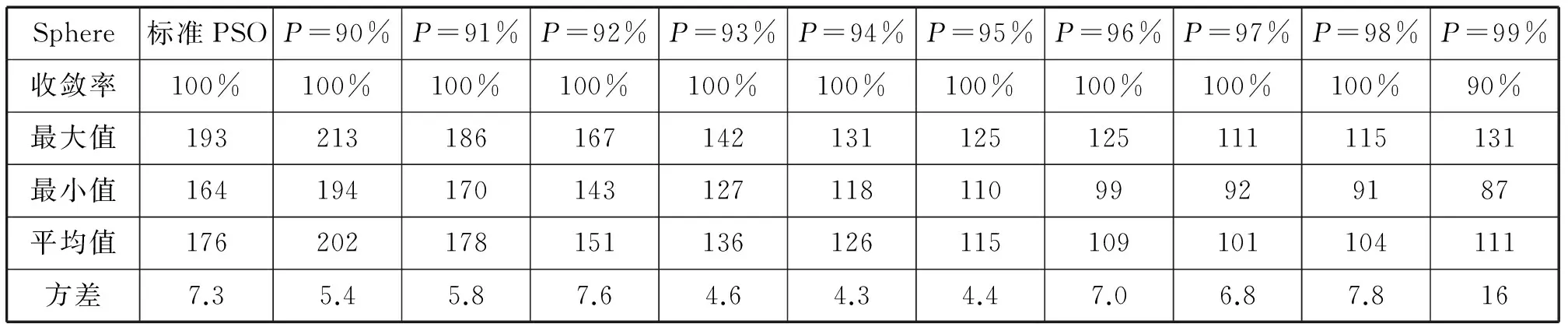
表2 NGPSO在不同置信度时Sphere函数的表现Tab.2 NGPSO at different degrees of confidence performance in the Sphere function
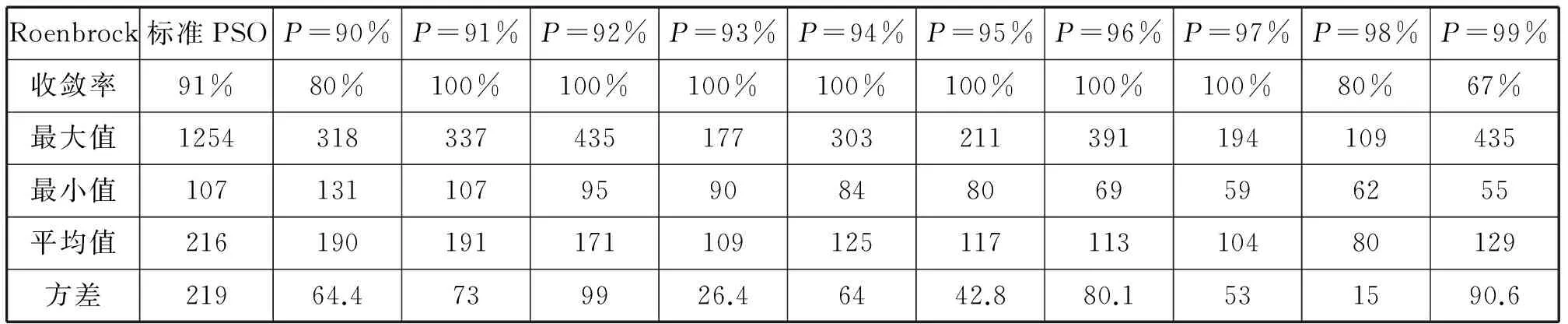
表3 NGPSO在不同置信度时Rosenbrock函数的表现Tab.3 NGPSO at different degrees of confidence performance in the Rosenbrock function
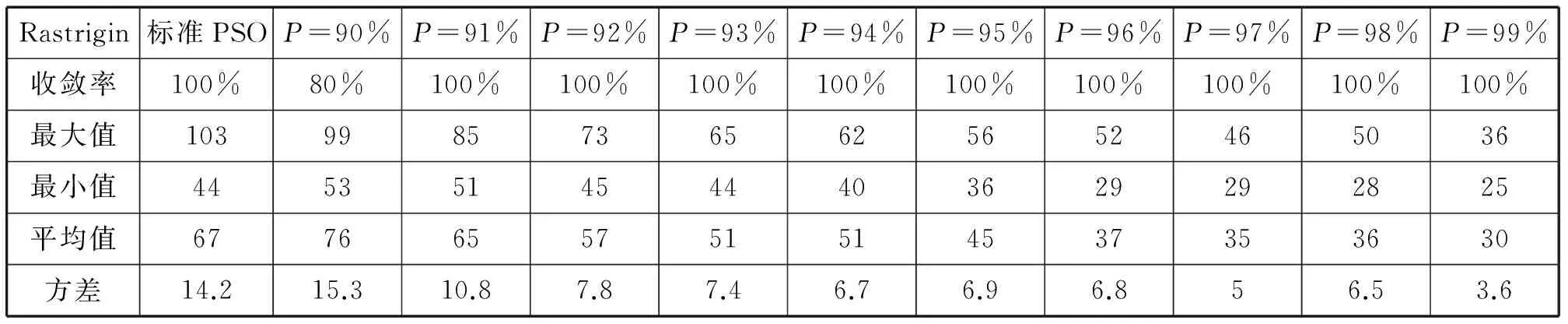
表4 NGPSO在不同置信度时Rastrigin函数的表现Tab.4 NGPSO at different degrees of confidence performance in the Rastrigin function
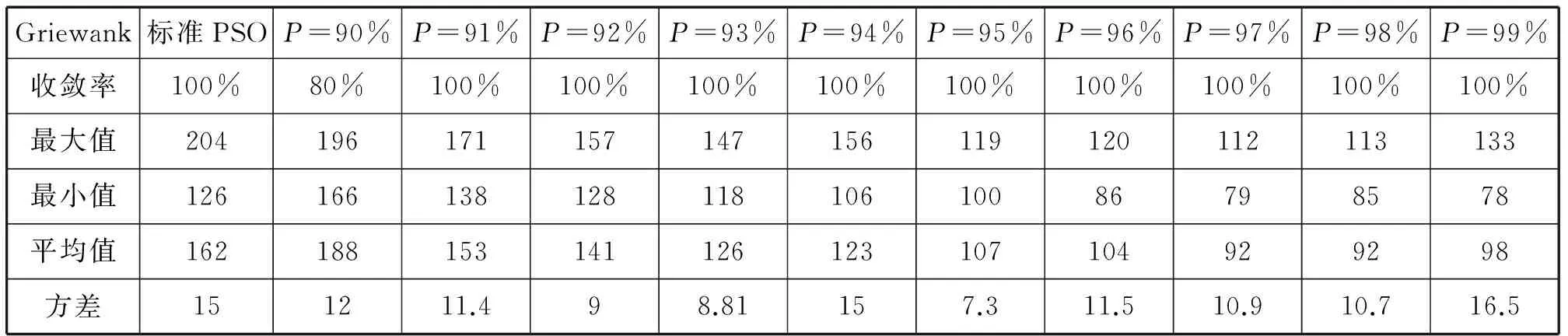
表5 NGPSO在不同置信度时Griewank函数的表现Tab.5 NGPSO at different degrees of confidence performance in the Griewank function
总结应用于四个标准测试函数上的仿真结果不难发现:新算法在置信度取97时,在每个测试函数上的综合性能都很好,收敛代数和收敛的稳定性都明显强于标准PSO算法。所以建议,之后分布可以选取本文列举的高斯分布即μ=0.5,P=97%即σ2=0.23的高斯分布取代标准PSO算法中的均匀分布。
4 改进的PSO算法应用于锅炉汽包水位系统
4.1 程序步骤
改进PSO算法优化串级三冲量锅炉汽包水位PID控制系统的参数步骤如下:
a.将PID控制系统的六个参数看作是一个六维空间中的某个解,确定解集的范围,即根据经验两对Kp、Ki、Kd三个参数的范围,确定PSO算法的参数,随机初始化粒子的位置、初速度、粒子的种群规模和迭代的最大次数。
b.PSO算法与PID控制的“接口”在适应度函数,所谓的接口就是使得PSO算法得到的数值应用于PID控制,所以选取合适的适应度函数非常重要。这个适应度函数将在之后的参数设定中介绍。
c.计算出每个粒子的适应值,判断出当前第一代粒子的当前全局最优Gbest,记录粒子第一代为粒子的当前个体最优Pbest.
d.根据公式(13)更新粒子的速度,公式(6)更新的粒子的位置,计算更新后的粒子适应值,与之前所得Gbest和Pbest相比较,得出每代的全局最优Gbest和粒子个体的历史最优Pbest.
e.判断是否满足终止条件,若满足,跳出;若不满足,循环至步骤4.
f.输出全局最优粒子,即PID控制系统的三个参数。
4.2 仿真实验
仿真时,设置如下参数:设置两对Kp、Ki、Kd的最小值为0.001,以免PID参数为0,而最大值设置为200,粒子的最大速度Vmax为6,种群规模为40,迭代次数为200.锅炉的被控对象数学模型参数采用文献[9]中的设置:
(15)
(16)
本文的仿真对象[10]是120t/h蒸发量的锅炉,其要求水位在[-50,50]mm内,阀门输入为4~20 mA,则水位变送器的传递系数:
γH=16/(2×50)=0.16
(17)
给水流量信号和蒸汽流量信号的传递系数为:
γW,γD=16/120=0.133
(18)
另外,通过估算得到给水流量信号和蒸汽流量分流信号的分流系数nW,nD均为0.21,适应度函数取系统各种性能的综合,设置为:
(19)
其中,y表示水位值,r表示设定值,tr表示上升时间,这里定义其为闭环系统第一次从0上升到0.9倍的时间,ω1、ω2、ω3、ω4、ω5表示加权系数。由于加权系数对于之后优化的PID参数有很大的影响,所以需要根据不同的系统要求来设定不同的值,本文暂时将ω1、ω2、ω3、ω4、ω5分别取0.45、0.55、0.65、0.45、2.
由于系统的环境和控制对象的状态在不断变化,所以适应度函数也在动态调整,本文在matlab中采用simulink模块,将改进PSO程序带入得到仿真模型图如下。
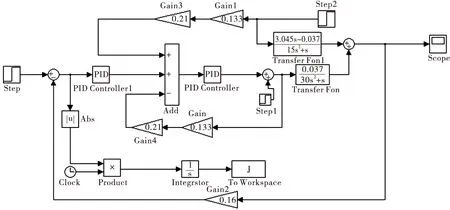
图4 锅炉汽包水位系统仿真模型Fig.4 Simulation model of boiler′s water-level system
在初始输入幅值为1的单位阶跃信号,在400 s和600 s加入蒸汽和给水扰动,得图5:
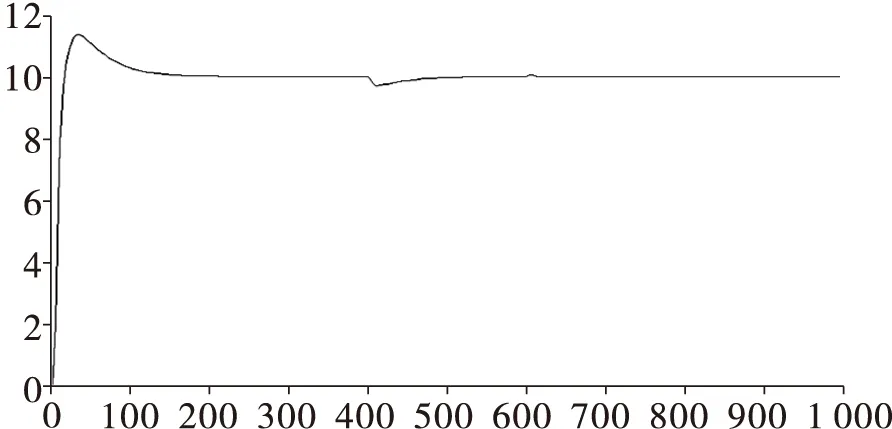
图5 改进的PSO算法整定的串级三冲量PID控制系统响应曲线Fig.5 Response curve of cascade three-impulse PIDcontrol system based on improved PSO tuning
图6是用Z-N法整定的锅炉汽包水位响应曲线图,与图5对比可知:由改进PSO算法整定的锅炉汽包水位具有较强的自适应性,超调量和稳定时间都变小很多,鲁棒性较强。
5 结束语
对标准PSO算法进行改进,得出新的收敛速度较快粒子群算法, 并将改进的粒子群优化算法与锅炉汽包水位串级三冲量控制系统相结合,动态整定PID参数,在matlab-simulink中进行仿真实验,得到较好的结果。改进PSO算法在收敛速度方面有较好的表现,但是改进算法的收敛精度相比标准PSO算法没有很大提升,所以在应用到实际问题中,与标准PSO算法相比,只能更快的得到结果,不能得到更优的结果。之后的工作首先是将改进PSO算法应用于更多的标准测试函数,观察选取不同参数的情况;其次是再次改进算法,将算法的收敛精度提高;最后希望本文的方法可以为之后的锅炉汽包水位系统设计提供新的思路。
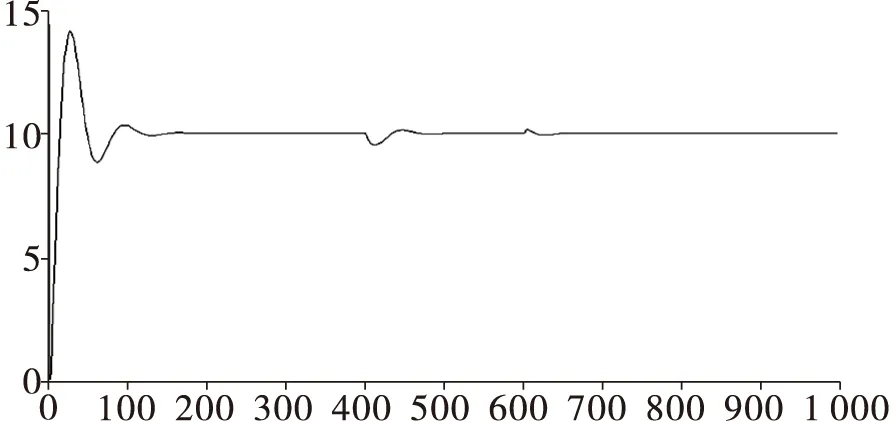
图6 串级三冲量PID控制系统响应曲线Fig.6 Response curve of cascade three-impulse PID control system
[1] 张松兰,何坚强,李先锋.锅炉汽包水位控制策略研究[J].自动化与仪器仪表,2008(6):1-3.
[2] 郑文杰,张习睿.基于模糊PID参数自调整的锅炉汽包水位控制设计[J].水利电力机械,2007,29(1):16-19.
[3] 王伟,张晶涛.PID参数先进整定方法综述[J].自动化学报,2000,26(3):347-355.
[4] KENNEDY J,EBERHART R C.Particle Swarm Optimization[C]∥Proceedings of IEEE International Conference on Neural Networks,Piscataway NJ:IEEE Service Center,1995:1942-1948.
[5] 鄢波,丁维明,魏海坤.工业锅炉汽包水位模糊自适应PID控制系统[J].发电设备,2006,20(4):276-279.
[6] ENGELBRECHT A P.计算群体智能基础[M].谭营译.北京:清华大学出版社,2009.
[7] 李俊吉,崔志华,崔炎,等.空间分割微粒群算法[J].太原科技大学学报,2010,31(1):19-25.
[8] JIANG M,LUO Y P,YANG S Y.Stochastic convergence analysis and parameter selection of the standard particle swarm optimization algorithm[J].Information Processing Letters,2007,102(1):8-16.
[9] 薛莉莉,沈晓群.锅炉汽包水位的模糊控制器设计与仿真[J].科技信息,2010(11):118-119.
[10] 何鑫,朱明清,王刚.锅炉汽包水位三冲量自适应模糊PID控制[J].自动化技术与应用,2012,31(11):21-24.
Water-level Control System of Boiler Drum Based on Improved Particle Swarm Optimization
WEI Jin-jun,ZHANG Wei,LIU Jiao,MA Di
(Department of Process Equipment and Control Engineering,Taiyuan University of Technology,Taiyuan 030024,China)
An improved particle swam optimization with Gaussian distribution from mathematical expectation position of particles is proposed to improve the convergence rate of Particle Swarm Optimization.The algorithm uses the properties of Gaussian random number selection.If Gaussian distribution selects the appropriate parameters,the algorithm will not only make the algorithm convergence faster,but also provide a mechanism to help algorithm jump out of local optimum.Through the results applied to the four standard test functions,Gaussian distribution choose parametersμ=0.5,P=97%(σ2=0.23)can help algorithm obtain better performance.Then the improved Particle Swarm Optimization was used on PID parameter tuning,in which PID will be used for the boiler drum level control system.Better results were achieved through the establishment of system model and the simulink in matlab.
particle swarm optimization,convergence rate,gaussian swarm,drum level
2015-04-15
国家青年基金(51106104)
魏晋军(1988-),男,硕士研究生,主要研究方向为智能优化算法及应用。
1673-2057(2015)06-0423-07
TP301.6;TP273.5
A
10.3969/j.issn.1673-2057.2015.06.003
