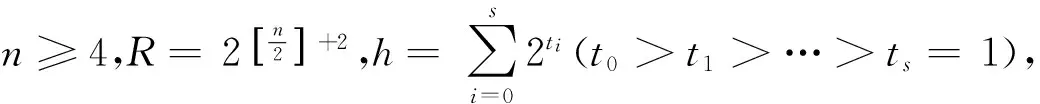BC网络的限制边连通度
2015-05-11王玉洁刘秀丽高晓慧
王玉洁,原 军,刘秀丽,高晓慧
(太原科技大学应用科学学院,太原 030024)
BC网络的限制边连通度
王玉洁,原 军,刘秀丽,高晓慧
(太原科技大学应用科学学院,太原 030024)
互连网络的可靠性评估对于多处理系统的设计和维护是非常重要的。限制边连通度是互连网络可靠性评估的一个重要参数,因此,研究限制边连通度对互联网络的可靠性评估具有重要意义。通过研究n-维双射连通互连网络(简称BC网络)的h-限制边连通度的性质,可推导得到n-维BC网络的h-限制边连通度的值。另外,因为BC网络包含若干著名的网络模型,比如,超立方体、莫比乌斯立方体、交叉立方体、扭立方体、生成扭立方体、广义扭立方体和M立方体,所以,应用推导得到的结果可以得出这些网络的h-限制边连通度。
BC网络;可靠性;限制边连通度;互连网络
众所周知,边连通度是反映图的连通性质的一个重要参数[1],而要更精确地刻画图的连通性质,经典边连通度存在着不足之处。为克服其缺陷,在文献[2]中引入了限制边连通度。限制边连通度是度量大型互连网络可靠性的一类重要参数。本文主要探究双射连通网络的限制边连通度。
双射连通网络(简称BC网络)是以立方体为背景的一系列网络,它包含许多著名的网络,如,超立方体、莫比乌斯立方体[2]、扭立方体[3]、交叉立方体[4]、生成扭立方体[5]、广义扭立方体[6]和立方体[7]。研究BC网络的性质,则可获得以上各种变形网络的性质。

1 预备工作和术语
设G=(V,E)是一个无向图,其中V=V(G),E=E(G)分别表示图G的顶点集和边集。假设V′是V的一个非空子集,以V′为顶点集,以两端点均在V′中的边的全体为边集所组成的子图,称为G的由V′导出的子图,记为G[V′].G的一条途径是指一个有限非空序列w=v0e1v1e2v2…ekvk,它的项交替地为顶点和边,使得ei(1≤i≤k)的端点为vi-1和vi,则称w是一条(v0,vk)途径。若途径w的顶点v0,v1,…,vk互不相同,则w称为路。G的两个顶点u和v称为连通的,如果在G中存(u,v)在路。
对于一个连通图G,F是G的一个边子集,若G-F不连通且G-F的每个分支至少有h个顶点,则称F为G的h-限制边割,记为λh-边割。G的最小λh-边割所含边数称为G的h-限制边连通度,记为λh(G).
定义1 一维BC图B1是只有两个顶点的完全图。一维BC图的类记为B1={B1}.一个图G是n-维BC图,记为Bn,若存在V0,V1⊂V(G)满足如下两个条件:
(1)V(G)=V0∪V1,V0≠Ø,V1≠Ø,V0∩V1=Ø,G[V0],G[V1]∈Bn-1;
(2)V0和V1之间的边集形成G的一个完美对集M.
n-维双射连通图Bn是n正则的,有2n个顶点和n2n-1条边。n-维BC图的集合称为它的类,记为Bn.为了具体讨论BC图,记V(Bn)为=X1X2…Xn={x1x2…xn∶xi∈{1,0},i=1,2,…,n}(事实上,这种表示方法与超立方体的表示类似)。因此,定义1中的V0和V1可分别表示为X1X2…Xn-10和X1X2…Xn-11.类似地,用X1X2…Xkzk-1…zn={x1x2…xkzk+1…zn∶xi∈{1,0},i=1,2,…,k,zj是固定的,j=k+1,…n}来表示Bn中的k-维BC子图。超立方体、扭立方体、交叉立方体、莫比乌斯立方体、生成扭立方体等都是对以上结论的应用,因此,此处省略了这些图的具体定义,只给出一些图(见图1-2),这些图将会呈现出将要使用的结构性质。
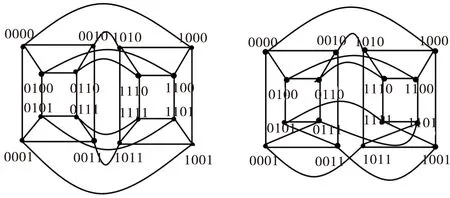
图1 Q4(左)和CQ4(右)Fig.1 Q4(left)and CQ4(right)
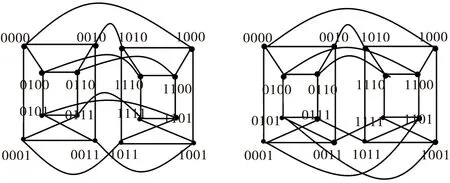
图2 TQ4(左)和LTQ4(右)Fig.2 TQ4(left)and LTQ4(right)
2 主要结果
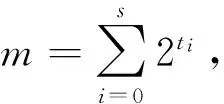
近年来,Zhang Mingzu,Meng Jixiang和Yang Weihua[13]等证得了以下结论。

引理2 若0≤q≤2c,则exq≤cq.
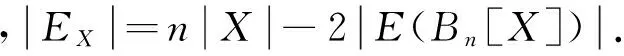
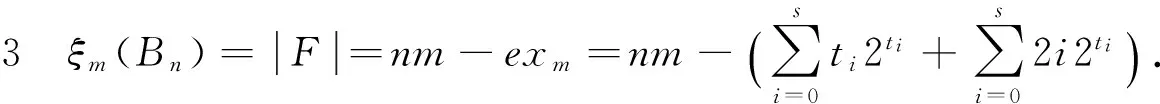
另外,由λh(Bn)和ξm(Bn)的定义,有λh(Bn)=min{ξm(Bn)∶h≤m≤2n-1}.
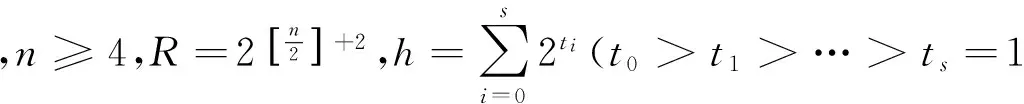
情况1 讨论exh-exh-1≤n.

情况2 讨论exh-1-exh-2≤n.

情况3 讨论exh-2-exh-3≤n.

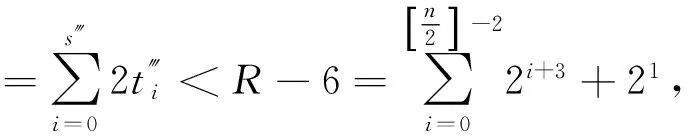
情况4 讨论exh-3-exh-4≤n.类似情况3的讨论方法,可得exh-3-exh-4≤n.
综上,则有exh-exh-4=(exh-exh-1)+(exh-1-exh-2)+(exh-2-exh-1)+(exh-3-exh-4)≤4n.证毕。

证明:由引理4,得ξh(Bn)-ξh-4(Bn)=nh-exh-n(h-4)-exh-4=4n-(exh-exh-4)≥4n-4n=0.因此ξh(Bn)=nh-exh关于h是不减的。证毕。
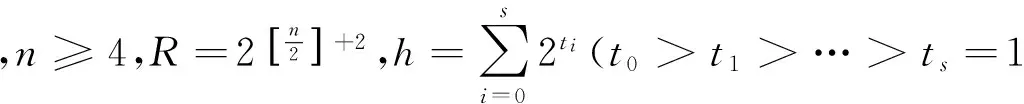
证明:分两种情况证明:
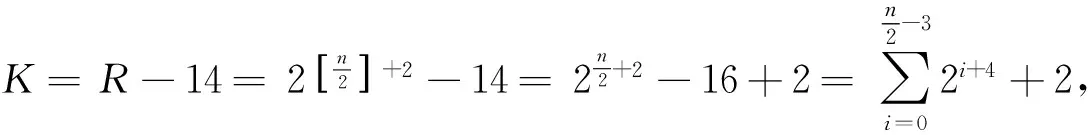
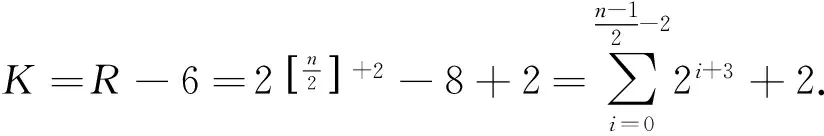
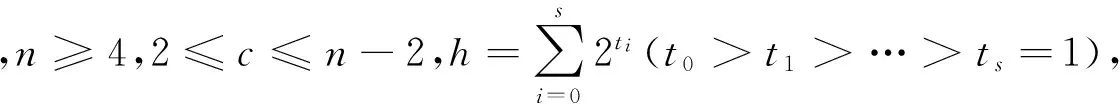


证明:引理7的直接推论。证毕。
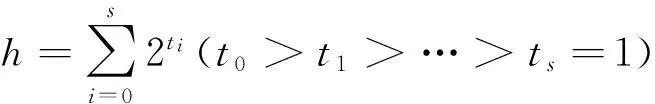

证明:当2≤c≤n-4时,因为2c+2≤h≤2c+1+2,所以设h=2c+2+p,(0≤p≤2c).由引理9,得exh=ex2c+2+exp+4p.又由引理2,exp≤cp.则有ξh(Bn)-ξ2c+2(Bn)=nh-exh-n(2c+2)+ex2c+2=np-(exp+4p)=(n-4)p-exp≥(n-4)p-cp=(n-4-c)p≥0.证毕。
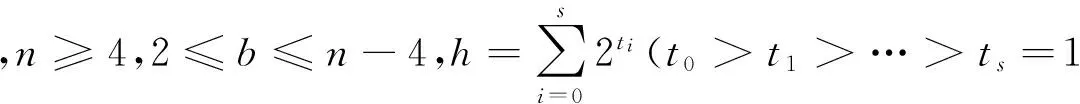
证明:结合引理7与引理10即可证。证毕。

证明:引理11的直接推论。证毕。
事实上,由引理11容易看出,ξh(Bn)的单调性走势是上升的。当h无限变大时,ξh(Bn)也将变大,即ξh(Bn)≥ξR-2(Bn)是成立的,也就是下面的观察13成立。
观察13 当b≥n-4时,若2b-2≤h<2n-1,易知,ξh(Bn)≥ξR-2(Bn).
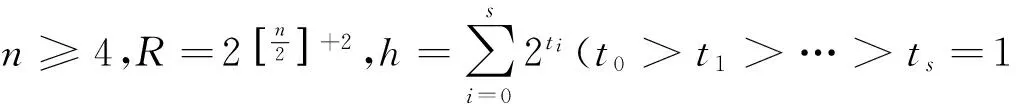
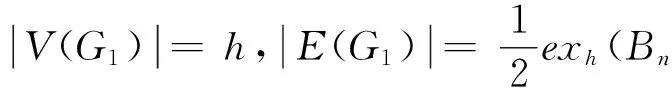
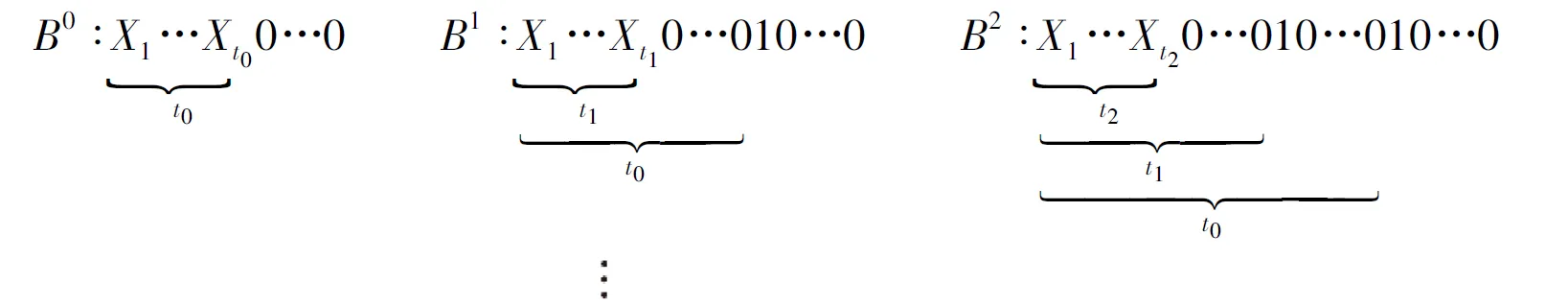

下证λh(Bn)≥nh-exh.假设F为最小的λh-边割,且C为阶为m的较小分支(Bn-F至少含有2个分支)。分两种情况证明:
(1) 首先假设2≤h (2)当K 由于BC网络包含Qn、MQn、TQn、CQn、LTQn、GTQn和MCQn.故研究BC网络的性质,则可获得以上超立方体的变形网络的性质,也就是下面的推论15成立。 [1] 段晋芳,原军.二部图2等周边连通度最优的充分条件[J].太原科技大学学报,2010,31(4):309-311. [2]CULLP.Thecubes[J].IEEETransactionsonComputers,1995,44:647-659. [3]HIBERSPAJ,KOOPMANMRJ,SNEPSCHEUTJVD.Thetwistedcube[C]∥ProceedingsoftheConferenceonParallelArchitecturesandLanguagesEurope,LectureNotesinComputerScience,Europe,1987:152-159. [4]EFEK.Avariationonthehypercubewithlowerdiameter[J].IEEETransactionsoncomputers,1991,40(11):1312-1316. [5]YANGXF,EVANSDJ,MEGSONGM.Thelocallytwistedcubes[J].IntJComputMath.2005,82(4):401-413. [6]CHEDIDFB.Onthegeneralizedtwistedcube[J].InformationProcessingLetters,1995,55(1):49-52. [7]SINGHVINK,GHOSEK.TheMcube:asymmetricalcubebasednetworkwithtwistedlinks[C]∥Proceedingsofthe9thIEEEInternationalParallelProcessingSymposium,SantaBarbara,CA,1995:11-16. [8]CHENYC,TANJJM,HSULH,KAOSS.Super-connectivityandsuperedge-connectivityforsomeinterconnectionnetworks[J].AppliedMathematicsandComputation,2003,140:245-254. [9]ZHUQ,XUJM.Onrestrictededgeconnectivityandextraedgeconnectivityofhypercubesandfoldedhypercubes[J].JUnivSciTechnolChina,2006,36:246-253. [10]ZHUQ,XUJ,HOUX,XUM.Onreliabilityofthefoldedhypercubes[J].InformationScience,2007,177:1782-1788. [11]ZHUQ,XUJ,LVM.Edgefaulttoleranceanalysisofaclassofinterconnectionnetworks[J].MathematicsandComputation,2006,172:111-121. [12]YANGW,LINH.ReliabilityevaluationofBCnetworksintermsofextravertex-andedge-connectivity[J].IEEETransactionsonComputers,2014,63(10):2540-2548. [13]ZHANGM,MENGJ,YANGW,TIANY.Reliabilityanalysisofbijectiveconnectionnetworksintermsoftheextraedge-connectivity[J].InformationScience,2014,279:374-382. Reliability Evaluation of BC Networks in Terms of the Extra Edge-connectivity WANG Yu-jie,YUAN Jun,LIU Xiu-li ,GAO Xiao-hui (School of Applied Sciences,Taiyuan University of Science and Technology,Taiyuan 030024) Reliability evaluation of interconnection network is important to the design and maintenance of multiprocessor systems.The restricted edge-connectivity is an important parameter for the reliability evaluation of interconnection network.Therefore,the study on the restricted edge-connectivity is of great significance to the reliability evaluation of interconnection network.We obtain the value ofh-extra edge-connectivity by researching the properties ofh-extra edge-connectivity of ann-dimensional bijective connection network (in brief,BC network).Besides,since the BC network includes several well-known network models,such as hypercubes,Möbius cubes,crossed cubes,twisted cubes,locally-twisted cubes,generalized twisted cubes andMcubes,so the application of our results can be launched theh-extra edge-connectivity of these networks. BC network,reliability,extra edge-connectivity,interconnection network 2015-04-17 国家青年科学基金(61402317);国家数学天元基金(11126076);山西省青年自然科学基金(2012021001-2) 王玉洁(1986-),女,硕士研究生,主要研究方向为图论及泛函分析。 1673-2057(2015)06-0480-06 O157.5 A 10.3969/j.issn.1673-2057.2015.06.014