基于Logistic回归模型确定权重的模糊综合评判法在边坡稳定性分析中的应用

2015-05-11饶运章张学焱

有色金属科学与工程 2015年6期

饶运章，张学焱

（江西理工大学资源与环境工程学院，江西赣州 341000）

模糊综合评判[1-7]是对受多因素影响的事物作出全面评价的一种十分有效的多因素决策方法.采用模糊综合评判方法可以将本来模糊的、主观性很大的定性评估转变为定量评判，适用于边坡这类影响事物因素较多，又具有很强的模糊性的稳定性综合评判.

模糊综合评判评价边坡稳定性过程中，需要确定各因素影响权重，传统确定权重的方法，主要有层次分析法和专家打分法2种，二者确定都具有一定主观性.本文采用Logistic回归模型确定权重，对赣南地区离子型稀土矿山边坡进行稳定性综合评判，避免了人为主观影响，具有较好的客观性.

1 模糊综合评判模型

1.1 确定评价等级和评价因子

根据工程经验[8-9]，当边坡安全系数大于其安全等级所规定的安全系数上限，认为边坡是稳定的；边坡安全系数处在上限和下限之间，认为边坡是较稳定的；边坡安全系数处在下限和1之间时，认为边坡是欠稳定的；边坡安全系数小于1时，认为边坡是不稳定的.故将边坡稳定性分为4个等级，即稳定、较稳定、欠稳定、不稳定.

赣南地区离子型稀土矿山滑坡类型主要属浅层风化松散岩土质滑坡，影响边坡稳定性的因素主要分为4大块：边坡地形地貌、边坡岩土力学参数、岩土体中水的作用、外部载荷.边坡地形地貌包括坡度、坡高、边坡的几何形态等；边坡岩土力学参数体现为重度、黏聚力、内摩擦角、渗透性等力学参数；岩土体中水的作用主要有注液强度和降雨；外部载荷主要有地震作用、坡顶荷载、支护作用.

稀土矿山边坡坡高一般不超过40m，对边坡稳定性影响很小[10]；赣南地区不属于地震多发地带，不考虑地震作用；对没有作支护拦挡工程的矿山，简化不考虑其人为扰动影响；稀土边坡岩土体中水的作用复杂，受降雨、渗透性、注液时间、注液量等多个因素影响，简化考虑采用孔隙水压力比（土体中一点的孔隙水压力与其上土层覆盖压力的比值）和容重来代替这些参数的变化.结合赣南地区稀土边坡的实际情况，综合考虑选取重度、内摩擦角、黏聚力、坡度、孔隙水压力比5个参数作为影响滑坡的主要因素.

根据42个边坡实例的（表2）统计结果并结合专家评定，确定评价等级及评价因子数值分布，如表1所示.

当孔隙压力比小于0.2、边坡角小于25°、内摩擦角大于42°、内聚力大于40 kPa、重度小于12 kN/m3时，边坡处于稳定状态；当孔隙压力比大于0.5、边坡角大于45°、内摩擦角小于18°、内聚力小于8 kPa、重度大于24 kN/m3时，边坡处于极不稳定状态.

1.2 模糊综合评判模型

根据模糊综合评判模型[11-12]设定2个有限论域：

其中U代表综合评判因子所组成的集合，V代表评判等级所组成的集合.

U和V可组成模糊评价矩阵R：

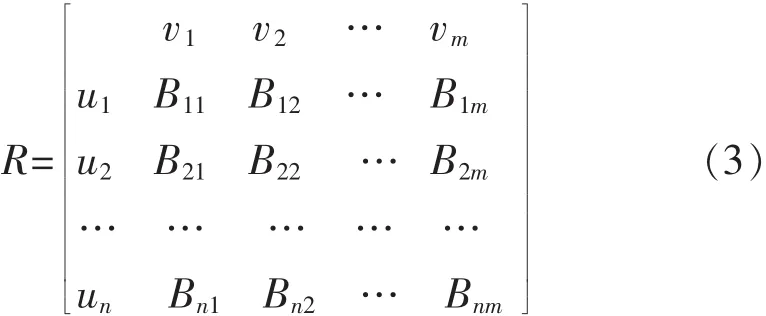
Bij表示i个因素属于j等级的隶属度.

设预测样本权重 A={r1，r2，…，rn}，则综合评判为：

C为综合评判输出的结果.

1.3 确定隶属度函数

所选的影响因子都是连续性指标，采用“降半梯形[13]”作为其隶属度函数，如式（5）～式（8）所示：

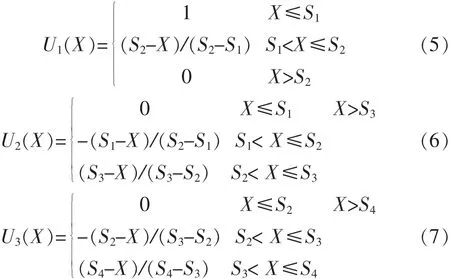
式（5）～式（8）中，将表 1 指标数据按从小到大排列，S1表示表1中指标的下边界值，S2表示第2组的组中值，S3表示第3组组中值，S4表示上边界值，如评价因子内聚力一栏中，S1=8、S2=16、S3=32、S4=40.U（X）表示对应的隶属度值.

2 逻辑回归模型确定权重

2.1 逻辑回归模型

逻辑回归的方法可以应用于求解滑坡概率[14]，逻辑回归模型可表述为：设P为发生滑坡的概率，则取值范围为[0 1]，那么（1-P）为不发生滑坡的概率，将两者的比值取自然对数得 ln[P/（1-P）]，令 Z=ln[P/（1-P）]，并作为因变量，将影响因子指标 Xi（i=1，2，…，n）作为自变量，建立线性回归方程：

式（9）、式（10）中，Bi（i=1，2，…，n）为回归常数，选择确定性系数指标CF作为影响因子指标Xi：

式（11）中：Pa为滑坡在a数据类中发生的条件概率，表示为影响因子子集a中滑坡的个数与边坡总数的比值；Ps为滑坡在整个数据中发生的先验概率，表示为总的数据中滑坡个数与边坡总数的比值.

2.2 SPSS运行求解回归系数

选用42个离子型稀土矿山实测边坡数据，如表2所示.采用各影响因子中最大值和最小值的差值确定步长，对边坡实例进行分类，按式（11）计算各子集确定性系数CF[14].根据各子集CF值，将42个边坡例子中的各个影响因子转化为CF值.应用SPSS软件，将各影响因子的CF值作为自变量，边坡状态作为因变量（稳定状态用-4值表示，按照式（10），Z=-4计算，此时滑坡概率为0.018，滑坡状态用4值表示，此时滑坡概率为0.982），进行线性回归，得出各回归项的回归系数[15-20]，如表3所示.

2.3 回归系数转化为权重

由式（10）可以推导得：

表2 实测边坡数据Tab le 2 Observed data of slope

表2 （续）实测边坡数据Table 2（continue） Observed data of slope

表3 各评价因子的回归系数Table 3 Regression coefficient of each evaluation factor

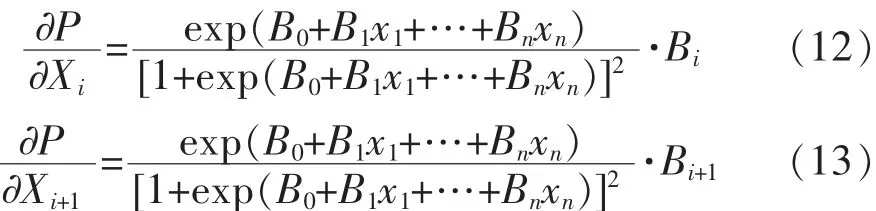
由式（12）、式（13）可知，不同的影响因子相互比较，对滑坡概率的影响梯度是与回归系数成正比的，如式（14）：

也就说，回归系数就是体现滑坡因子作用于滑坡概率权重的大小，本文采用回归系数应用计算权重.对表3中的回归系数进行归一化处理，得到各影响因子的权重，如表4所示.

表4 各影响因子权重Table 4 Each im pact factor weights

3 实例运算

龙南县东江乡足洞试验矿某边坡矿层土容重为20 kN/m3、内摩擦角29.1°、内聚力25 kPa、边坡角24.5°、孔隙水压力比0.44，可得其评价矩阵为：

代入权重向量A=[0.031 0.145 0.093 0.539 0.191]，计算得：

由最大隶属度原则，说明边坡处于稳定状态.边坡实际处于试验开采阶段，处于注液初期，稳定性良好，评判结果与实际相符.

4 结束语

模糊综合评判适用于边坡稳定性分析.采用Logistic回归模型确定权重的模糊综合评判法应用于边坡稳定性分析，较传统的确定权重的方法增加了客观性，使结果更让人容易接受.同时相对纯粹的统计回归分析边坡稳定性的方法，增加了主观性，减少了存在个别边坡变异性带来的稳定性分析偏差.缺点是，采用逻辑回归模型需要较多的统计数据.

[1]张勇慧,李红旭,盛谦，等.基于模糊综合评判的公路岩质边坡稳定性分级研究[J].岩土力学,2010,31(10):3151-3156.

[2]李建峰,万臣,赵勇.高寒高海拔地区岩质边坡稳定性评价研究[J].重庆交通大学学报,2015,34(2):45-49.

[3]王树仁,周洪彬,武崇福，等.采用综合评判方法确定工程岩体力学参数研究[J].岩土力学,2007(28):202-206.

[4]洪海春,徐卫亚,叶明亮.基于模糊综合评判的边坡稳定性分析[J].河海大学学报,2005,33(5):558-562.

[5]孙树海,曹兰柱,张立新.露天矿边坡稳定性的模糊综合评判[J].辽宁工程技术大学学报,2007,26(2):177-179.

[6]彭振斌,何忠明,彭文祥，等.模糊评判在岩质边坡稳定性分析中的应用[J].矿冶工程,2005,25(3):1-4.

[7]刘端伶,谭国焕,李启光,等.岩石边坡稳定性和Fuzzy综合评判法[J].岩石力学与工程学报,1999，18(2):170-175.

[8]毛巨省.模糊综合评判在边坡稳定性评价中的应用[J].西安科技大学学报,2010,30(5):609-612.

[9]刘华丽,卢厚清,李宏伟,等.模糊综合评判法在边坡稳定性分析中的应用[J].解放军理工大学学报,2013,14(1):84-88.

[10]殷昊,刘飞,杜立新,等.黄土高原区地形与植被分布规律对滑坡发生概率的影响[J].现代地质,2010,24(5):1016-1021.

[11]陆俊.基于模糊综合评判的滑坡预报模型及其应用[J].水土保持研究,2009,16(5):241-244.

[12]谢全敏.滑坡灾害风险评价的系统分析[J].岩土力学,2005,26(1):71-75.