计算弱水侵气藏单井动态控制储量的简单方法

2015-05-10刘振平刘启国王宏玉袁淋

重庆科技学院学报（自然科学版） 2015年3期

刘振平刘启国王宏玉袁淋

(西南石油大学油气藏地质及开发工程国家重点实验室，成都 610500)

利用水驱气藏物质平衡方程计算气井的控制储量时，一般必须先计算水侵量。常用的水侵量计算模型包括稳态模型、非稳态模型和拟稳态模型。非稳态模型又分为平面径向流系统模型、直线流系统模型和半球形流系统模型［1］。这些水侵量的计算方法比较繁琐和复杂，且必须在满足假设条件的情况下才能应用［2-3］。

胡俊坤等人利用气藏初期不产水时的不稳定试井资料结合二项式产能方程计算气藏目前的气相渗透率，再根据相对渗透率曲线确定气藏目前的含水饱和度，计算气藏的存水体积系数，最终得到气井的控制储量［4］。该方法虽然避免了要首先求取水侵量来计算气井控制储量的麻烦，但其需要的资料繁多，且计算过程复杂。同年，胡俊坤等人还绘制出了水驱气藏无因次视压力与采出程度的理论特征图版，利用实际数据拟合图版的方法来求取气井的控制储量和水侵量［5］。该方法较为成熟，但是图版绘制和数据拟合需要编写程序才能满足工程精度需求，其推广受到限制。

本次研究提出一种新的解决思路，将水驱气藏物质平衡方程左右两边分别独立成新的方程，然后，利用新方程之间的关系，通过简单调整参数的方法，可以直接得到气藏存水体积系数和单井控制储量。

1 水驱气藏物质平衡

李传亮给出水驱气藏物质平衡方程式［6］:

式中:p、pi— 气藏当前地层压力、原始地层压力，MPa;

Z、Zi—储层当前条件下、初始条件下的天然气偏差因子;

G、Gp— 气井的控制储量、累计采气量，108m3;

Cc— 气藏容积压缩系数，MPa-1。

其中，气藏容积压缩系数为:

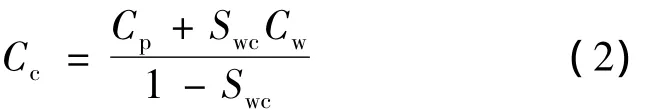
式中:ω—气藏的存水体积系数;

Sw、Swi— 当前气藏含水饱和度、原始含水饱和度;

We— 气藏水侵量，m3;

Wp— 累计产水量，m3;

Bw—地层水的体积系数;

Bgi—原始地层条件下天然气的体积系数。

由式(3)可得水侵量:

2 气井控制储量和水侵量的求解方法

式中:Cp—岩石孔隙压缩系数，MPa-1;

Swc—束缚水饱和度;

Cw— 地层水压缩系数，MPa-1。气藏存水体积系数为:

对于弱水侵气藏，可以认为气藏的存水体积系数为常数。将式(1)左边记为:

式(5)右边虽然没有直接出现累计产气量Gp，但是地层压力p、生产压差△p都是直接和累计产气量Gp有关的变量。同时，随着存水体积系数w的增大，直线y1(Gp)-Gp的斜率和截距都会减小。这是因为同一口气井产液能力是比较稳定的，存水体积系数w越大，则水侵量就越大，地层的压力越能得到补充，采出单位体积气体地层压力下降的越小，直线斜率也就越小。从数学角度来看，分析式(5)易得:随着存水体积系数w的增大，同一个Gp对应的y1(Gp)的值就越小，直线y1(Gp)-Gp的截距和斜率也就越小。

将式(1)右边记为:

观察式(6)可以发现，直线截距始终为pi/Zi，与控制储量G的取值无关。随着控制储量G的增大，直线斜率会越来越小。

利用同一口井不同时刻的试井数据和生产数据，假设一个存水体积系数w，应用式(5)就可以做出直线y1(Gp)-Gp。同理，对于式(6)假设一个控制储量G就可以做出一条直线y2(Gp)-Gp。

当气井的控制储量G和存水体积系数w都为真实值的时候，利用式(1)绘制的物质平衡曲线会为一条直线。所以，此时直线y1(Gp)-Gp和直线y2(Gp)-Gp也会完全重合。

由于直线y2(Gp)-Gp的截距是固定的，所以，首先通过调整存水体积系数w的值，使直线y1(Gp)-Gp的截距与其相同。然后，再通过改变控制储量G的值，使直线y2(Gp)-Gp的斜率和修正后的直线y1(Gp)-Gp斜率相同。控制储量G的初值可用封闭气藏物质平衡方程作图进行估算，然后，逐步减小范围进行搜索。当直线y1(Gp)-Gp和直线y2(Gp)-Gp完全重合时，对应的w、G即为该井的实际存水体积系数和控制储量。再利用式(4)和该井的生产数据就可以计算水侵量We。

3 实例验证

某弱水侵气藏的一口水平井平5井，于2010年2月投产，至今总共进行了5次压力测试。岩石孔隙压缩系数Cp为1×10-4MPa-1，地层水压缩系数Cw为 4 ×10-4MPa-1，束缚水饱和度 Swc为 0.277，原始地层条件下天然气的体积系数Bgi为0.003 6，地层水的体积系数Bw为1.03。根据该井的压力测试数据、生产数据和天然气组分报表统计并计算出该井的相关数据，结果如表1所示。

表1 平5井基础数据表

应用式(5)和表1 中的数据，取 w=0，0.1，0.2，绘出对比图(图1)。

图1 平5井不同存水体积系数时y1(G p)-G p直线对比图

观察图1可以发现，随着存水体积系数ω的增大，直线y1的斜率和截距都在变小。

应用式(6)和表1中的数据，分别取G为25，30，35 绘制图2。

图2 平5井不同控制储量G时y2(G p)-G p直线对比图

观察图2可以发现，随着控制储量G的增大，直线y2的截距始终为37.743，但直线斜率越来越小。对比图1和图2中拟合直线的截距可以确定，该井的存水体积系数ω在0～0.1之间。

调整存水体积系数ω，当ω =0.021 1时直线y1与直线y2的截距相等，这样方程y1就确定了。然后，再调整控制储量G的值使得直线y2的方程与修正后的直线y1相同，此时得出的控制储量G=23.19×108m3就为该井的实际控制储量。所以，该井的控制储量为23.19×108m3，存水体积系数为0.021 1，拟合效果见图3。而按照定容封闭气藏处理得到的动态控制储量却为25.60×108m3，比本次计算的动态控制储量多了2.09×108m3。