安全高效跟驰状态下的后车行为控制

潘 登， 梅 萌， 郑应平

(同济大学 电子与信息工程学院， 上海 201804)

车辆跟驰控制的研究，特别重视行车安全和线路运能的充分利用，以及车辆行为调整的平稳(舒适)性。Jiang等[1]提出全速差模型FVDM(Full Velocity Difference Model)仿真交通流的相移和阻塞的演化。针对驾驶行为、紧急情况和避免冲突，以及消除不切实际的加速度，Zhao和Gao[2]建立了全速差、全加速度差模型FVADM(Full Velocity and Acceleration Difference Model)，能够较好地仿真车辆跟驰行为，但未深入讨论对速度和加速控制的同步控制问题。Peng等[3]引入相关系数建立了一个能避免冲突和消除过高加速度的最优速差模型，但相关系数的动态确定尚无切实可行的有效方法。Panwai和Dia[4]提出一个神经智能体跟驰模型(Neural Agent Car-following Model)，考虑了后车的反应时间，较好地解释了车辆跟驰过程中的行为细节，然而神经网络对训练数据的完备性要求较高，在面临未曾遭遇的跟驰状况时难以取得较好的效果。除了考虑车辆跟驰运行的安全性、高效性和平稳(舒适)性之外，交通系统还必须具有在扰动情况下恢复正常行车秩序的能力，例如铁路行车计划制定时预留一定的时、空裕量，在列车运行图因故不能正常执行时，将有助于正常行车秩序的恢复。Baskar等[5]对智能运输系统体系架构的设计方案的相关论述，无疑将拓宽车辆跟驰问题研究的视野。Pan和Zheng[6-8]提出一种基于安全跟驰车距实时跟踪的新速差控制方法，并将这种新的速差控制方法用于高速列车的稳态跟驰运行，但未注意到车辆行为优化目标与行为调整单元始末时间的关系，本文拟对此深入研究，将跟驰时隙TG(Time Gap)引入该算法，并从安全高效跟驰稳态拓展到安全高效跟驰状态。

本文首先讨论安全跟驰车距的实时计算，为后续列车(下称后车)行为调整提供必要的依据；而后基于后车行为调整单元的始末时间，研究其安全、高效和平稳(舒适)运行的控制律；建立后车行为调整的控制模型；最后通过仿真实验分析、验证控制方法的有效性，并对未来持续研究进行展望。

1 安全跟驰车距的实时计算

安全跟驰车距，简称安全车距，是后车调整自身行为的重要依据之一，一般随着跟驰形势的变化而变化。Mulder等[9]设计了一个主动减速控制算法，将安全放在首要位置，体现了安全第一的原则。当实际车距小于安全车距，安全性存在一定的风险，后车应减速运行以扩大车距，必要情况下可采取紧急停车措施以避免与前行列车(下称前车)发生冲突；当实际车距大于安全车距，安全性无虞但跟驰效率却可能有待进一步提高。图1描述了给定速度条件下安全车距的一般计算方法。

前车与后车应保持的安全车距LSafe为

LSafe=Lf-Lp+ΔL

( 1 )

式中：Lp、Lf分别为前、后车的制动距离;ΔL为安全裕量。

如果Lp=0，安全车距的计算基于车辆采取的绝对制动模式[10]；如果Lp≠0，安全车距的计算则基于车辆采取的相对制动模式[10]。

按照绝对制动模式和相关文献[11]，可得安全车距LSafe随速度V变化的拟合函数[12]

LSafe=f(V)=

0.810 26V2+48.722 08V+281.595 58

( 2 )

应当指出，图1描述了世界范围内铁路运输领域在工程上广泛采用的列车安全间隔计算方法，尽管能够给出相对安全车距的计算公式，但其也仅仅适用于前、后列车速度相同条件下的相对安全车距的计算，并不能适用于前、后列车速度不同的一般情形。文献[13-14]仅给出某速度条件下的列车紧急制动距离限值或安全追踪间隔(即安全跟驰车距，亦可基于某一运营速度以最小间隔时间的形式给出[14])作为指导性标准， 文献[15]也仅仅给出限速目标距离的静态计算公式和若干速度下的限速目标距离，并未给出全速域范围内任意跟驰形势下列车应当遵循的制动距离标准或限速目标距离标准，由于初速度和目标速度在全速域内有无数种组合，以及用来表征列车控制策略的加速度在数值上也表现出纷繁的多样性，很难在工程上通过静态计算穷尽任意跟驰形势下列车的限速目标距离值，更惶论任意跟驰形势下限速目标距离的实时计算，实际中往往在牺牲效率确保安全的原则下以较高速度下的限速目标距离作为自身行为调整的约束条件或优化目标。列车(跟驰)运行控制正是基于此当前现状，无论准移动闭塞系统(CTCS-3级列车运行控制系统)，还是移动闭塞系统(CTCS-4级列车运行控制系统)，均采取“distance-to-go”控制(即目标距离速度控制)方式[16]，当实际车距大于规定的目标距离时，列车按规定速度行驶，当实际车距小于或等于规定的目标距离时，列车按一次连续制动曲线减速运行，直到实际车距重新大于规定的目标距离方能按规定的速度行驶。一次连续制动曲线，相同速度条件下按目标距离的不同，分为常用制动速度曲线和紧急制动速度曲线两种情况：当目标距离为常用制动距离时，列车采用常用制动速度曲线减速停车；当目标距离为紧急制动距离时，列车采用紧急制动速度曲线减速停车(注：准移动闭塞系统和移动闭塞系统中，常用制动距离和紧急制动距离的确定需要考虑通信延时、制动措施生效延时等因素，替换为“常用制动安全间隔”、“紧急制动安全间隔”似乎更为合适。本文遵循传统的表达方式，望不致读者误解)。目前，在世界范围内尚无任何国家能够给出任意速度条件下列车的紧急制动距离限值标准和常用制动距离标准，并在列车跟驰控制中加以使用。“distance-to-go”控制方式从工程角度巧妙地解决了准移动闭塞系统和移动闭塞系统中的列车跟驰控制问题，就列车运行控制安全性和高效性的综合考量，其所体现出的在思想上的先进性和技术上的优越性，是固定闭塞系统广泛采用的分级速度控制方式所无可比拟的。然而“distance-to-go”控制方式中的“目标距离”，仅能凭借文献[15]给出的静态计算公式经计算得到若干初速度和目标速度组合条件下的限速目标距离，以作为列车运行控制的依据，并非针对全速域范围内相对制动模式下前、后列车速度不同且速度为任意值的一般情形的限速目标距离实时计算而提出，因而不能在列车跟驰运行过程中的任意时刻都做到跟驰安全性和高效性的“综合最优”，往往在“安全第一”原则的指导下以牺牲“跟驰的效率”为代价，准移动闭塞系统和移动闭塞系统的优势并未得到充分发挥；另一方面，“distance-to-go”控制方式下，只有常用制动速度曲线或紧急制动速度曲线被触发时，列车才会按照该曲线减速运行，而常用制动速度曲线或紧急制动速度曲线未被触发时，列车如何在受控条件下实现安全、高效和平稳运行，两种制动曲线并不能给出有效地解决方案。因此，有必要根据未来移动闭塞系统列车运行控制的技术需求，采取将相对安全车距的计算“分而治之”再“有机统一”的策略，即先计算绝对安全车距，在跟驰过程中再根据前车的速度、控制策略和最不利情形(譬如前车紧急制动，以及前方蹋方或断轨等突发事件)实时地确定是否继续计算相对安全车距。采取数值拟合方法建立绝对安全车距关于后车速度的拟合函数，可以解决全速域范围内一般跟驰情形任意速度条件下绝对安全车距的计算问题，不仅能够作为一种“依据(标准)”为列车跟驰运行控制所遵循，而且为后车根据前车行为状态和控制策略实时计算相对安全车距创造了必备的前提条件。这样，列车在跟驰运行过程中可根据路况(如塌方、断轨等)、行车命令(如定点停车等)和能否可靠获得前方列车信息等具体行车条件合理选择相应的安全车距计算模式，并进行相应模式下的列车运行控制，从而达到安全、高效行车的目的。

为突出全速域范围内一般跟驰情形任意速度条件下绝对安全车距计算的重要性，同时不影响学术表达，本文采用式( 2 )计算安全跟驰车距。

2 后车行为调整的控制律

2.1 控制律的计算

安全高效跟驰状态下：若前、后车速度相同，称为“安全高效跟驰稳态”，后车无需调整自身行为；若前、后车速度相异，任其发展安全高效跟驰状态势必被破坏，当实际车距在安全车距的右半邻域内，后车应科学调整自身行为，以保证实际车距始终处于安全车距的右半邻域内，并最终复归于安全高效跟驰稳态。这里，引入“安全高效跟驰稳态”邻域内速差控制方法[6-8]讨论后车行为调整的控制律计算问题。

(1) 基于后车行为调整单元初始时刻的计算方法

按照式( 2 )以后车行为调整单元初始时刻的后车速度计算安全车距，安全高效跟驰状态下，后车行为调整控制律的计算以后车行为调整单元初始时刻前、后车的运行速度为依据，并将此初始时刻的前车速度作为后车行为调整单元结束时刻的末速度。因为安全车距根据后车行为调整单元的初始速度计算而得，故该控制律计算方法称为“基于后车行为调整单元初始时刻的计算方法”。

假设前、后车之间实际车距为L，则L-LSafe的时间导数为

( 3 )

式中:Vf表示后车速度。

如果L一直等于LSafe，那么安全跟驰的效率将是最高的。也就是说，后车安全高效地进行自身行为调整，应满足下式

( 4 )

实际车距L可以根据前、后车的位置和线路曲率和坡度等参数计算而得。不失一般性和不影响学术思想的表达，这里主要论述车辆直线跟驰运行的情形。这样有

L=Sp-Sf

( 5 )

式中:Sp、Sf分别为前、后车位置。由于

( 6 )

由式( 2 )、式( 4 ) 和式( 6 )可得

( 7 )

即

( 8 )

式中:af为后车调整自身行为的加速度;Vp为前车运行速度。

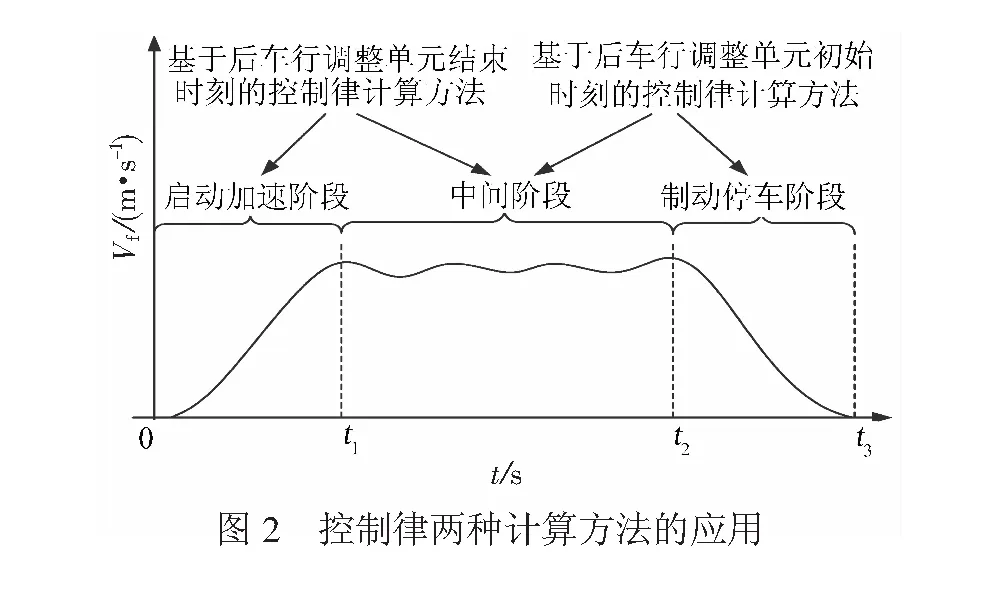
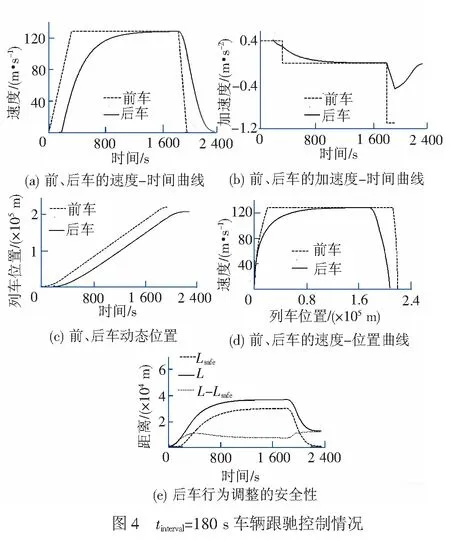
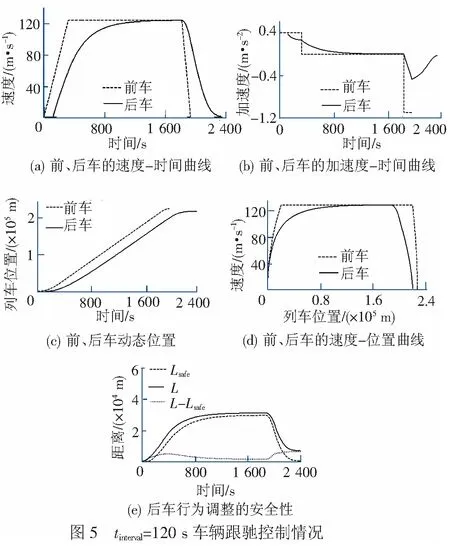
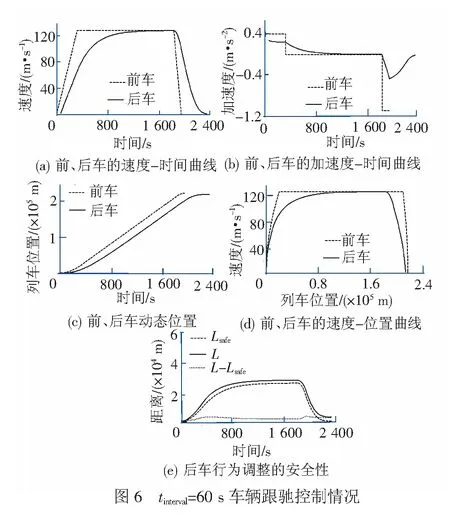
在安全车距的邻域内，易见：若Vp>Vf，后车加速运行以提高跟驰效率；若Vp=Vf，后车可保持当前速度匀速运行；若Vp

(2) 基于后车行为调整单元结束时刻的计算方法

按照式( 2 )以后车行为调整单元初始时刻的前车运行速度(即后车行为调整单元结束时刻的末速度)计算安全车距，安全高效跟驰状态下，后车行为调整控制律的计算以后车行为调整单元初始时刻前、后车的运行速度为依据，并将此初始时刻的前车速度作为后车行为调整单元结束时刻的末速度。由于安全车距是根据后车行为调整结束时刻应达到的末速度计算而得，故该控制律计算方法称为“基于后车行为调整单元结束时刻的计算方法”。

将V=Vp代入式( 2 )可得根据后车行为调整结束时刻的末速度计算的安全车距

48.722 08×Vp+281.595 58

( 9 )

后车行为调整的控制律计算式为

(10)

2.2 控制律的平稳(舒适)性评估

从式( 8 )可见，如果前车速度Vp过大，基于后车行为调整单元初始时刻的控制律计算方法可能会导致后车在启动加速阶段过高的加速度，从而造成平稳(舒适)性不满足要求；从式(10)看，如果Vf远远大于Vp，基于后车行为调整单元结束时刻的控制律计算方法可能会导致后车在制动停车阶段的加速度(负值)过低，同样会造成平稳(舒适)性不满足要求。因此，从车辆行为调整的平稳(舒适)性考虑，在后车的启动加速阶段，基于后车行为调整单元初始时刻的控制律计算方法可能不适用，而基于后车行为调整单元结束时刻的控制律计算方法则更为适宜；在后车正常制动停车阶段，基于后车行为调整单元结束时刻的控制律计算方法则可能不适用，使用基于后车行为调整单元初始时刻的控制律计算方法则更为合适；后车其它行为调整阶段(即介于启动加速与制动停车之间的中间阶段)，由于前、后车速差较小，两种计算方法得出控制律的平稳(舒适)性均能满足要求。上述定性分析见图2。

下面根据两种后车行为调整的控制律计算方法，对车辆行为调整的平稳(舒适)性分别进行定量分析：

(1) 基于后车行为调整单元初始时刻的计算方法

由平稳(舒适)性双极性评估标准[17]，后车行为调整的控制律及平稳(舒适)性条件为

(11)

因为基于后车行为调整单元初始时刻的控制律计算方法不适用于车辆启动加速阶段，全面考虑其它行为调整阶段的极端情况，可知

(12)

令

(13)

地面车辆速度一般不超过500 km/h，假设Vf∈[0,500 km/h]，可得

maxg(Vf)=0.617 09

(14)

显然，|af|<0.63总是成立。也就是说，在安全高效跟驰状态下，除了启动加速阶段，基于后车行为调整单元初始时刻的控制律计算方法能够保证后车在其它阶段行为调整的平稳(舒适)性。

(2) 基于后车行为调整单元结束时刻的计算方法

对基于后车行为调整单元结束时刻的控制律计算方法，其控制律与平稳(舒适)性满足下列条件

(15)

考虑后车启动加速阶段的极端情形，可得

(16)

令

(17)

可知

maxg(Vp)=0.617 09

(18)

因此，安全高效跟驰状态下后车启动加速阶段，基于后车行为调整单元结束时刻的控制律计算方法能够确保其跟驰运行过程中的安全性、高效性和平稳性。

3 车辆跟驰控制模型

车辆跟驰控制模型见图3。其中，ap、Vp、Vp0、Sp、Sp0分别为前车的初始速度、初始位置，Vf0、Sf0分别为后车的初始速度、初始位置，并且 ΔV=Vp-Vf、L=Sp-Sf。

前、后车通过单位合力(加速度)来调整其自身行为，后车行为调整受到前车运行状态、行为调整策略和两车空间关系，以及自身行为调整优化目标的约束。

4 案例分析

假设前车行为过程分为3个阶段：第1阶段，前车以加速度ap=0.400 m/s2从0 m/s加速运行，直到速度为127.778 m/s；第2阶段，前车以127.778 m/s速度匀速运行1 500 s；在第3阶段，前车以加速度ap= -1.1 m/s2减速运行直至完全停止运行。

以前车位置和启动加速运行的初始时刻作为参考，可得前车的运动学公式

(19)

同理，可以得到后车的运动学公式

(20)

式中:tinterval为车辆间隔时间。 这里，取tinterval为180 s、120 s、60 s和0仿真控制律实施后后车的行为调整情况，见图4～图7。

从图4(b)、图5(b)、图6(b)、图7(b)可以看出，前车的加速度ap为若干阶跃信号的叠加，它驱使系统状态发生变化，后车按照行车组织的时隙要求和行为优化目标，以合理的加速度af进行适应性行为调整。

后车从静止状态按照规定时隙启动，并与前车形成跟驰关系。在前、后车以相同速度匀速运行之前，后车行为调整的控制律采取“基于后车行为调整单元结束时刻的计算方法”，故后车持续加速运行，直至安全高效跟驰稳态被建立起来，即前、后车以相同的速度和合理地间隔跟驰运行，安全性与高效性得到了较好的兼顾和均衡，见图4(a)～4(d)至图7(a) ～7(d)。当前车以-1.10 m/s2加速度减速停车时，后车行为调整的控制律采取“基于后车行为调整单元初始时刻的计算方法”，以平稳(舒适)的行为调整过程(见图4(e)、图5(e)、图6(e)、图7(e)和图8)实现了安全、高效跟驰运行。图8中的纵坐标Jerk为后车行为调整的冲动值，即后车加速度的时间导数。

图8显示后车的行为调整满足平稳(舒适)性的另一评判标准。除了加速度的幅值[17]之外，文献[18]将“冲动值”作为另一评估标准。文献[17-18]指出，冲动值的绝对值小于2 m/s3才能满足人们对平稳(舒适)性的要求。

随着车辆跟驰时隙的减小，新的速差公式不仅能够显著提高跟驰效率，而且能够以平稳(舒适)的行为调整确保后车运行的安全性。

安全性和高效性存在“悖论”问题。从图4(e)、图5(e)、图6(e)、图7(e)可以看出，实际车距L总是大于安全车距Lsafe，其中L-Lsafe随着时隙tinterval的提高而增加。这一方面说明了在跟驰关系建立的初始时刻合理确定安全车距邻域的重要性，另一方面适当的安全车距邻域(通过时隙tinterval确定)可为行车组织提供一定的时空裕量，用以特殊情况下恢复正常的行车秩序。

5 结束语

车辆跟驰距离的动态控制能够通过后车行为的科学调整来实现；后车行为调整必须充分考虑前车行为变化对跟驰车距的影响，特别是在前车行为驱动跟驰车距变化的趋势方面加强定量分析、预测，将是后车在科学控制下安全、高效跟驰运行的关键。前、后车之间以及车辆与车站或控制中心之间的高质量数据通信，是后车了解前车运行状态和自身跟驰行为质量的前提条件和技术基础，只有“知己知彼”，后车才能在跟驰运行过程中因时而动、因势利导，通过自身行为的科学调整实现跟驰车距的动态、合理控制。应当注意到，本文的研究成果是建立在车辆绝对制动模式的基础上的，尽管后车能够根据前车的行为变化采取适应性行为调整措施，但前车的行为状态和调整策略考虑得还远不不够充分，相对制动模式下的控制律将有助于安全行车前提下进一步提高后车行为调整的效率。另一方面，本文研究的主要内容为安全高效跟驰状态下的后车行为调整问题，即为安全车距邻域内的跟驰控制问题，车辆跟驰系统从非安全或非高效跟驰状态经过控制达到安全高效跟驰状态，以及时滞问题，需要在未来的研究中逐步展开并深入研究。

参考文献：

[1] JIANG R, WU Q S, ZHU Z J. Full Velocity Difference Model for a Car-following Theory[J]. Physical Review E, 2001, 64(1): 017101-1- 017101-4.

[2] ZHAO X, GAO Z. A New Car-following Model: Full Velocity and Acceleration Difference Model[J]. European Physical Journal B, 2005, 47(1): 145-150.

[3] PENG G H, CAI X H, LIU C Q. Optimal Velocity Difference Model for a Car-following Theory[J]. Physics Letter A, 2011, 375(45): 3973-3977.

[4] PANWAI S, DIA H. Neural Agent Car-following Models[J]. IEEE Transactions on Intelligent Transportation Systems, 2007, 8(1): 60-70.

[5] BASKAR L D, SCHUTTER D B, HELLENDOORN J, et al. Traffic Control and Intelligent Vehicle Highway Systems:A Survey[J]. IET Intelligent Transport Systems, 2011, 5(1): 38-52.

[6] PAN D, ZHENG Y. Velocity Difference Control Based on Dynamic Tracking of Safe Following Distance in the Process of Vehicle Following[J]. IET Intelligent Transport Systems, 2014, 8(3): 232-243.

[7] 潘登, 郑应平. 基于安全车距实时标定的列车间隔动态控制[J].交通运输工程学报, 2014, 14(1): 112-118.

PAN Deng, ZHENG Ying-ping. Dynamic Control of Train Interval Based on Real-time Calibration of Safe Headway[J]. Journal of Traffic and Transportation Engineering, 2014, 14(1): 112-118.

[8] PAN Deng, ZHENG Ying-ping. Dynamic Control of High-speed Train Following Operation[J]. Promet-Traffic & Transportation, 2014, 26(4): 291-297.

[9] MULDER M, PAUWELUSSEN J A, PAASSEN V M, et al. Active Deceleration Support in Car Following[J]. IEEE Transactions on Systems, Man and Cybernetics. Part A: Systems and Humans, 2010, 40(6): 1271-1284.

[10] HENKE C, TICHY M, SCHNEIDER T, et al. Organization and Control of Autonomous Railway Convoys[C]// Proceedings of the 9th International Symposium on Advanced Vehicle Control.Tokyo: Society of Automotive Engineers of Japan, 2008:1-6.

[11] 黄问盈, 杨宁清, 黄民. 我国铁道列车紧急制动距离限值核定原则的探讨[J].中国铁道科学, 2003, 24(5): 84-90.

HUANG Wen-ying, YANG Ning-qing, HUANG Ming. Standard of Railway Train Emergency Braking Distance Limit in China[J]. China Railway Science, 2003, 24(5): 84-90.

[12] 潘登, 郑应平. 高速列车追踪运行的控制机理研究[J]. 铁道学报, 2013, 35(3): 53-61.

PAN Deng, ZHENG Ying-ping. Study on the Mechanism of High-speed Train Following Operation Control[J]. Journal of the China Railway Society, 2013, 35(3): 53-61.

[13] 中华人民共和国铁道部. 铁路技术管理规程[M]. 北京: 中国铁道出版社, 2006.

[14] 铁道部科学技术司，铁道部运输局. 铁道部科技运[2008]4号 CTCS-3级列控系统总体技术方案(V1.0)[S].北京：中国铁道出版社，2008.

[15] 铁道部科学技术司，铁道部运输局.铁道部科技运[2010]138号列控中心技术规范 [S].北京：中国铁道出版社，2010.

[16] 傅世善. 闭塞与列控概论 第二讲 列控系统的速度控制模式[J]. 铁路通信信号工程技术, 2004, (6): 40-42.

FU Shi-shan. Introduction to Railway Block Systems and Train Control Systems (Second Lecture): Speed Control Mode of Train Control Systems[J]. Railway Signalling & Communication Engineering, 2004,(6): 40-42.

[17] International Organization for Standardization. ISO2631-4 Mechanical Vibration and Shock-Evaluation of Human Exposure to Whole-body Vibration -Part 4: Guidelines for the Evaluation of the Effects of Vibration and Rotational Motion on Passenger and Crew Comfort in Fixed-guide Way Transport Systems[S]. London: British Standards Institution, 2001.

[18] MARTINEZ J, CANUDAS-de-Wit C. A Safe Longitudinal Control for Adaptive Cruise Control and Stop-and-go Scenarios[J]. IEEE Transactions on Control Systems Technology, 2007, 15(2):246-258.