RV减速器扭转刚度特性分析
2015-05-10杨玉虎朱临宇陈振宇沈兆光
杨玉虎,朱临宇,陈振宇,沈兆光
(天津大学机构理论与装备设计教育部重点实验室,天津 300072)
RV减速器扭转刚度特性分析
杨玉虎,朱临宇,陈振宇,沈兆光
(天津大学机构理论与装备设计教育部重点实验室,天津 300072)
以广泛应用于机器人关节的 RV减速器为对象,针对其结构特点,构建了减速器整机的几何模型,以及在ANSYS环境下考虑轴承刚度、轮齿啮合刚度及各构件弹性的有限元模型,分析得出了对应曲柄轴自转 1周的整机扭转刚度的变化规律;与实验结果比较,验证了该模型的有效性与计算精度.在此基础上,应用该模型进一步分析了摆线轮与针齿啮合齿数以及轴承刚度变化对整机扭转刚度的影响规律.结果表明:轴承刚度是影响整机扭转刚度变化的主要因素;在分析整机扭转刚度特性时,将轴承刚度按非线性变化规律考虑时能够更精确地揭示整机的扭转刚度特性.
RV减速器;扭转刚度;轴承刚度;啮合刚度;
扭转刚度是RV减速器的一项重要性能指标.针对该类减速器刚度特性的分析与研究一直是研究热点.目前针对单级摆线传动的刚度特性分析已较为深入,其研究内容主要侧重于啮合刚度分析与建模研究,考虑因素不仅涉及主要构件的弹性,同时也计及摆线轮与针齿间不同接触位置的啮合刚度,以及多齿接触下变形协调等复杂影响因素[1-2].RV减速器也是一种包含摆线传动的二级封闭式行星传动系统,其低速级同为摆线传动,但传动结构与单级摆线区别较大,扭转刚度特性也有所不同.因此,国内外学者针对该类减速器刚度特性的研究仍在深入.张大卫等[3]基于Hertz理论建立了摆线针轮啮合刚度模型,利用石川公式简化了渐开线齿轮啮合刚度的计算.张迎辉等[4]进一步考虑了摆线轮齿廓曲率的影响,避免了单对齿啮合刚度为负的情况,使啮合刚度模型更加精细.Park[5]针对减速器的拓扑结构特点建立了整机扭转刚度半解析模型.Kim 等[6]在文献[5]计及轴承的模型基础上,考虑了减速器中摆线轮与曲柄轴铰接处的轴承弹性,将轴承等效为一个具有一定刚度的柔性圆环,研究结果表明,轴承刚度是影响整机扭转刚度的主要因素.上述研究使整机扭转刚度模型逐渐精细,但在轴承刚度方面均以线性方式进行处理,而相关文献指出,轴承刚度会随载荷发生非线性变化[7];在RV减速器中,不同啮合位置下各轴承受力的改变会引起轴承刚度的变化,因此需要进一步研究这种变化对此类减速器扭转刚度产生的影响.
为建立精细的整机扭转刚度有限元模型,本文不仅考虑了上述因素,还进一步考虑了摆线轮与针齿啮合齿数、轴承刚度随载荷变化的非线性特征对扭转刚度的影响规律.本研究可为该类减速器扭转刚度的建模提供一种方法上的借鉴.
1 拓扑结构与几何建模
RV传动是由渐开线与摆线齿轮组成的二级封闭式行星轮系,一种RV减速器的三维模型及其机构简图如图1所示.
高速级为渐开线齿轮组成的 K-H型差动轮系,由中心轮1、径向均匀分布的3个行星轮2及系杆7组成;低速级为摆线齿轮组成的K-H-V型行星轮系,由径向均匀分布的3个曲柄轴3、2个对称布置的摆线轮4与4′、若干针齿5以及输出盘6组成.该轮系中系杆7与输出盘6固连为同一构件.
3个偏置方向一致的曲柄轴,其一端分别与对应的3个行星轮固连,另一端与输出盘上对应的销孔组成转动副,中部与摆线轮构成转动副.
轮系传递运动时,行星轮带动曲柄轴转动,通过曲柄轴将行星轮的自转传递给摆线轮实现公转,而摆线轮又通过输出盘将其自转反馈给系杆作为差动轮系的输入运动,从而构成封闭式行星传动.
选取表 1和表 2数据(额定负载扭矩为3.136,MN·mm)构建减速器几何模型,建模中忽略各零部件上的倒角、螺纹孔等对刚度影响不大的局部细小结构,假定将针齿视为与针齿壳固连.在 Pro/E环境下构建几何模型,如图1(a)所示.
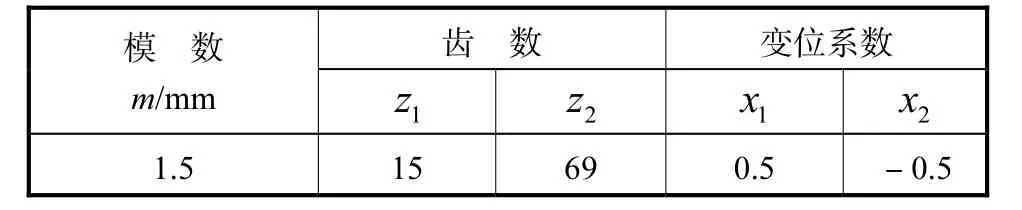
表1 减速器渐开线行星传动机构基本参数Tab.1 Fundamental parameters of involute planetary transmission mechanism of reducer

表2 减速器摆线行星传动机构基本参数Tab.2 Fundamental parameters of cycloidal planetary transmission mechanism of reducer
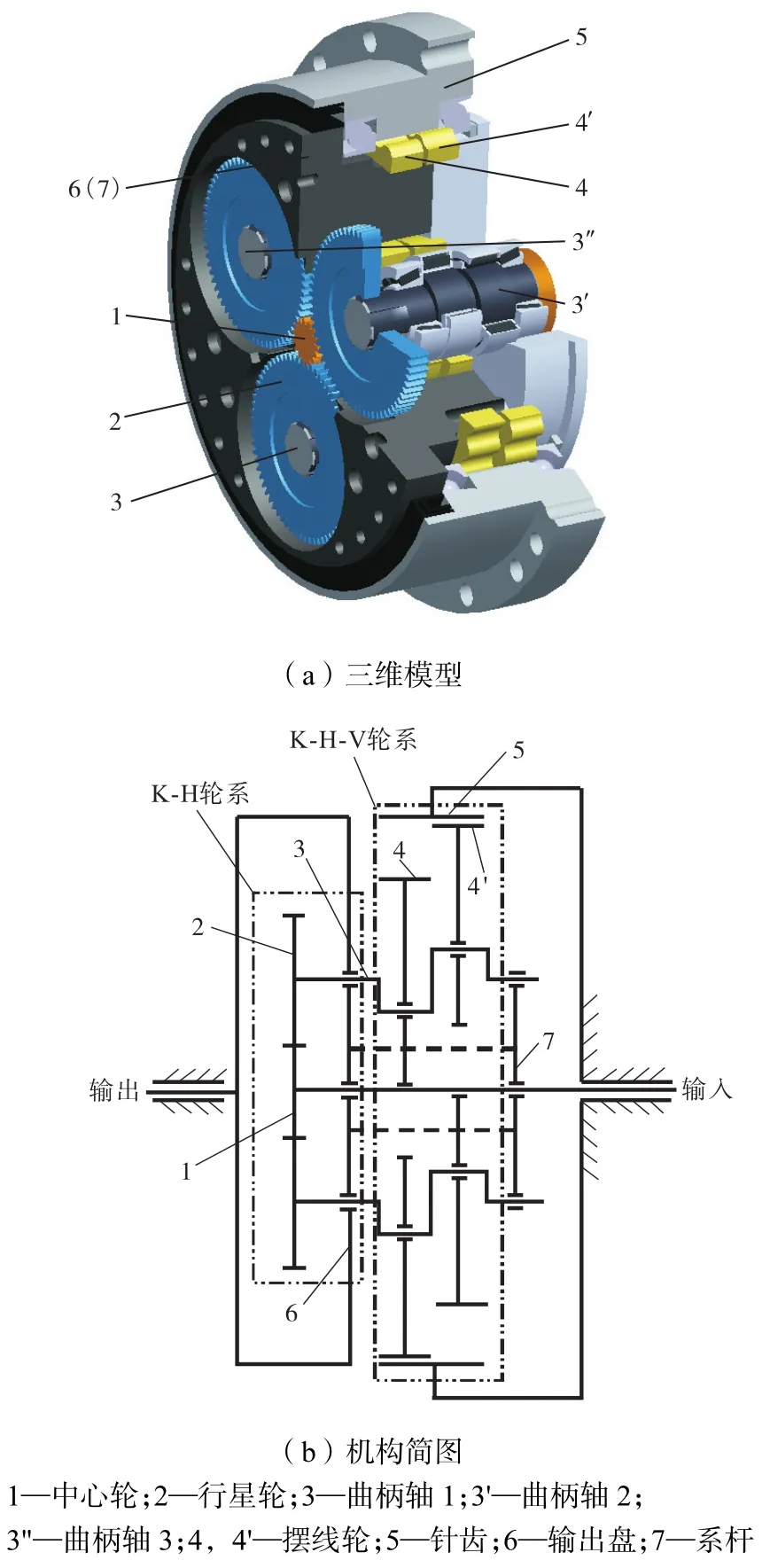
图1 RV减速器示意Fig.1 Schematic of RV reducer
2 整机扭转刚度建模
针对减速器的结构特点,在建模中除考虑主要构件弹性外,还需要计及以下影响整机扭转刚度的主要因素.
(1)轴承刚度:包括曲柄轴与摆线轮相连的转臂轴承以及系杆与曲柄轴相连的支撑轴承的刚度.
(2)啮合刚度:包括渐开线齿轮与摆线齿轮的啮合刚度.摆线轮同时与多个针齿啮合,其啮合齿数随曲柄轴转角而变化,因而摆线轮与针齿的啮合刚度也会发生变化.
2.1 轴承刚度
2.1.1 初始位置及坐标系
相关研究[7]指出,轴承刚度会随外部载荷发生非线性变化,因此有必要对轴承进行受力分析.
设针齿 1与摆线轮齿根啮合的位置为轮系运动的初始位置,针齿逆时针方向依次编号 1,2,3,…,如图2所示.

图2 针齿编号Fig.2 Numbers of pins
对应针齿与摆线轮任意啮合位置,以中心轮回转中心O为原点,建立与曲柄轴自转运动固连的动坐标系Oxyz,使y轴与曲柄轴偏心方向一致,z轴与曲柄轴线方向重合,如图3所示.
固定减速器输入端,在输出端施加扭矩T后,曲柄轴的受力如图 3所示.图中HO为曲柄轴回转中心,1a、2a、b、c分别表示曲柄轴相应轴段的长度.HF为行星轮对曲柄轴的作用力,1R、2R分别为2个支撑轴承对曲柄轴的作用力,tF、xF、yF为转臂轴承对曲柄轴的切向作用力、x向作用力和y向作用力,HF、1F垂直于系杆HOO,xF、yF分别与相应的坐标轴重合.

图3 曲柄轴受力分析Fig.3 Schematic of force analysis of crank shaft
2.1.2 转臂轴承受力
曲柄轴及其轴承在运动过程中既承受摆线行星传动一级的输入载荷,亦承受该级输出载荷,故为该减速器的核心构件.假设 3根曲柄轴均匀地承受摆线行星传动机构的输入输出载荷,对机构进行受力分析,得到曲柄轴上与2个摆线轮形成转动副的2个转臂轴承的切向受力tF、x向受力xF和y向受力yF[8-9]分别为

式中:K1为短幅系数,K1= azp/rp;T为输出盘额定负载扭矩,N⋅ m m ;i为减速器传动比.
由于 Fx、Fy与坐标轴重合且 F1始终垂直于系杆OOH,故对应曲柄轴转过任意转角θ时,可以得到曲柄轴分别与 2个摆线轮铰接的转臂轴承在坐标系Oxyz下的合力R和 R′为

式中:iH= zp/zc;n为曲柄轴的编号,如图1所示,n= 1,2,3.
2.1.3 支撑轴承受力
行星轮对曲柄轴的力 FH[8-9]可表示为

支撑轴承对曲柄轴的作用力主要用于平衡摆线轮和行星轮对曲柄轴的作用力,其中摆线轮对曲柄轴的切向作用力 Ft以及行星轮对曲柄轴的切向作用力FH在支撑轴承处引起的切向力 R1t和 R2t可表示为

另一方面,xF、yF在支撑轴承处引起的作用反力1xR 、1yR 、2xR 、2yR 可表示为

设曲柄轴转过任意角度θ时,支撑轴承所承受的合力1R和2R在坐标系Oxyz下可表示为

2.1.4 轴承刚度
轴承刚度与载荷R的表达式[10]为
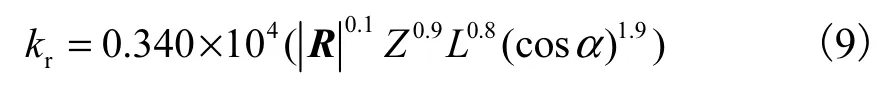
式中:rk为轴承刚度,N/mm;Z为滚子数目;L为滚子的有效长度,mm;α为滚动体接触角,(°).
减速器样机所用轴承基本参数如表3所示.

表3 轴承基本参数Tab.3 Fundamental parameters of bearings
将式(1)~式(8)计算结果代入式(9),可得各轴承刚度随曲柄轴转角θ的变化,如图4所示,图中pqk为构件p与构件q之间轴承的刚度.
2.2 啮合刚度
摆线轮与针齿间的啮合刚度是该类减速器扭转刚度的重要组成部分,同时啮合齿数是影响摆线轮与针齿啮合刚度的主要因素,因此,确定同时啮合齿数及啮合针齿号是准确建立该减速器扭转刚度的关键环节.
根据文献[11]可知,理想的摆线齿廓与标准针齿啮合时,有一半针齿同时与摆线轮啮合.然而考虑机构几何误差和摆线轮修形等因素的影响后,若不计及构件弹性变形的补偿作用,摆线轮与针齿间的多齿啮合条件将不复存在,而变为当某一针齿与摆线轮接触后,其余针齿与摆线轮间存在大小不等的初始间隙,间隙量由几何误差和摆线轮的修形量等因素综合确定.显然,要使针齿进入啮合,必须先克服其与摆线轮间的初始间隙.
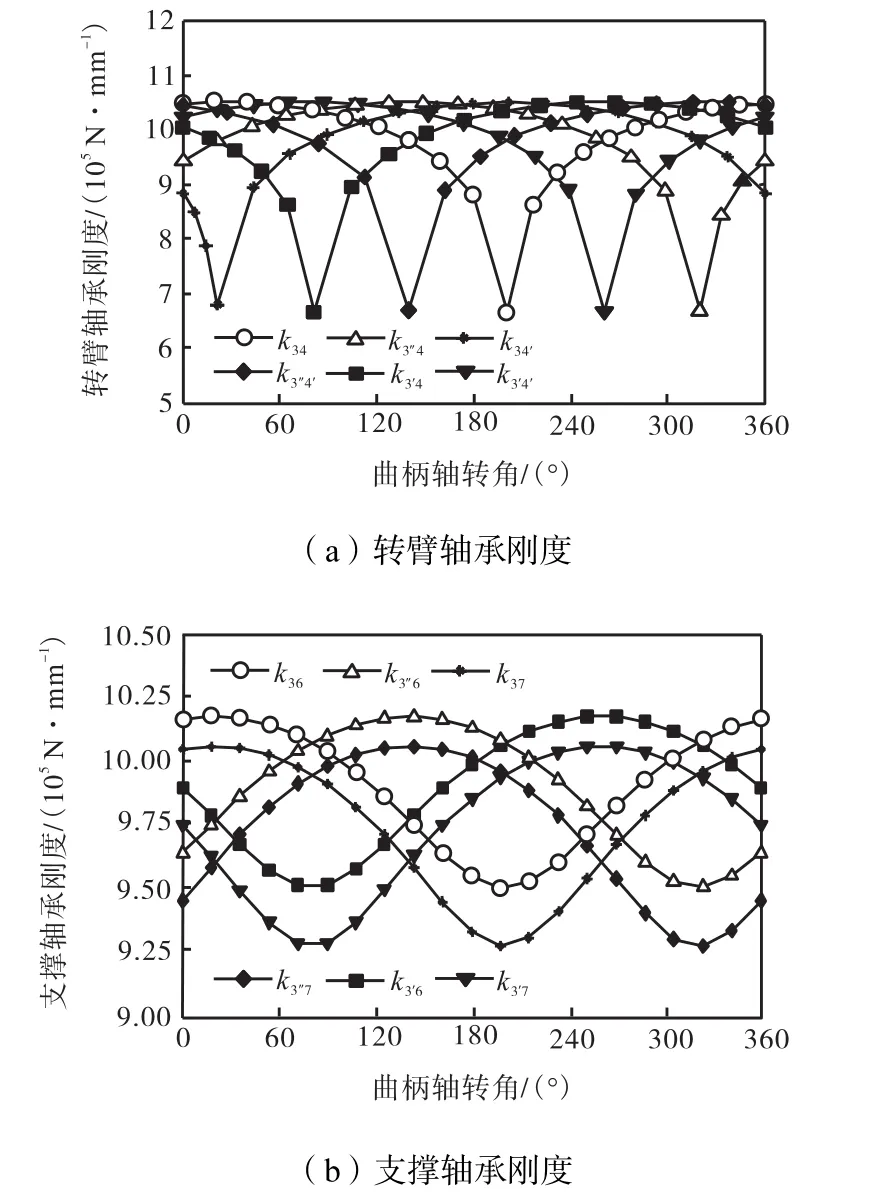
图4 轴承刚度变化Fig.4 Variation of bearing stiffness
另一方面,机构承载后,针齿和摆线轮在啮合点处会发生变形.由变形协调条件可知,各啮合点处的变形量与该点啮合力臂呈正比.显然,与摆线轮在啮合力臂较大的啮合点进行啮合的针齿首先克服间隙而进入啮合.
摆线轮与针齿同时啮合齿数与机构具体的误差、修形及载荷参数有关,通常为4~7[11-12].本文的仿真算例先以同时啮合齿数为5进行计算,后续将进一步研究啮合齿数对扭转刚度的影响.啮合针齿号可通过啮合点对应的啮合力臂确定,力臂越大,越先进入啮合.
图5为某一时刻与摆线轮啮合的5个针齿所对应的啮合力臂,图中cO、pO、rO分别表示摆线轮、针轮以及针齿的几何中心,P为摆线轮与针轮的瞬时运动中心.由图5中△rpO O P可知

式中kθ为针齿k与摆线轮啮合点对应的曲柄轴的转角.进而求得任一啮合针齿对应的力臂表达式为
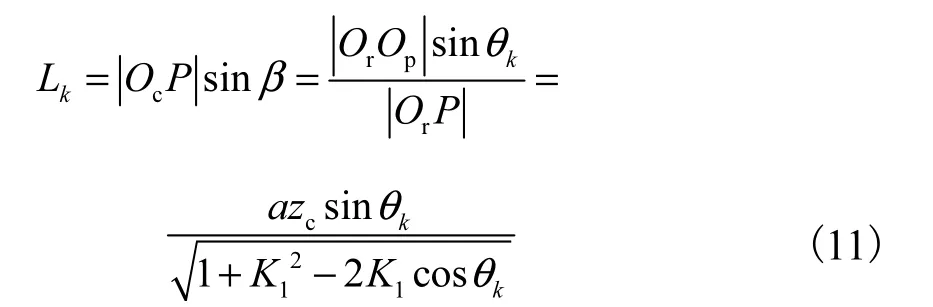
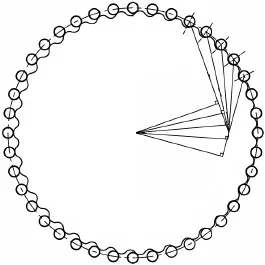
图5 啮合力臂Fig.5 Arm of meshing force
通过上述方法确定啮合针齿数和针齿号后,可绘制曲柄轴回转 1周过程中摆线轮与各针齿的啮合状态,如图6所示.

图6 摆线轮与针齿啮合状态示意Fig.6 Schematic of meshing state between cycloidal gear and pin gear
由图6可以直观地看出,参与啮合的针齿随曲柄轴位置的变化进行轮换.本文假设摆线轮与针齿在啮合过程中始终保持n个齿同时接触.
2.3 网格划分与边界条件
为保证建模精度与计算效率,需对模型分块处理.将减速器中曲柄轴、系杆、输出盘等形状规则的构件进行整体自动划分;将涉及接触分析的构件,如太阳轮与行星轮间、摆线轮与针轮间的啮合处进行局部网格划分,同时对网格大小与数量进行控制,以确保网格质量,防止畸变.该模型划分网格总数为89,275,节点数为 203,049,其局部网格划分结果如图7所示.
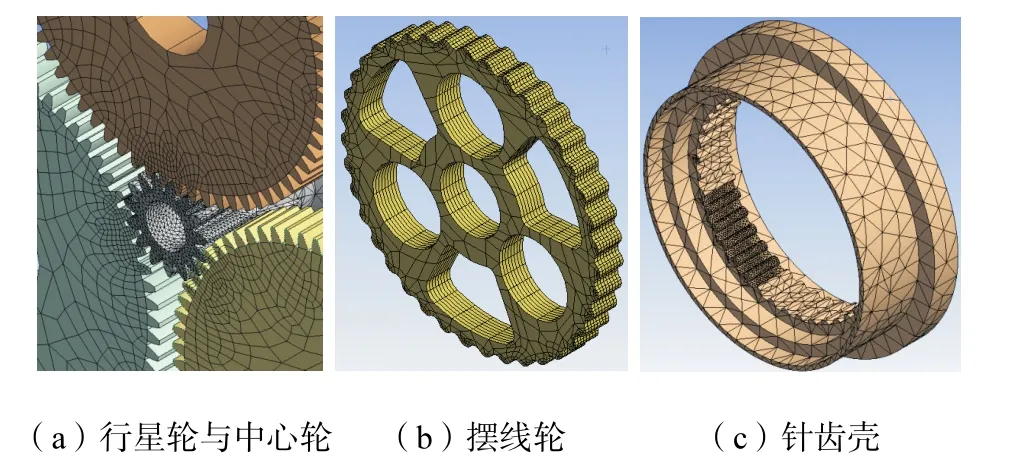
图7 局部网格Fig.7 Local meshes
在ANSYS环境下,根据表4设置各构件的材料参数,计入弹性.根据该机构的拓扑关系设置各构件间的连接方式.针对曲柄轴的具体位置导入对应轴承刚度数值,并设置摆线轮与针齿的啮合齿数和位置.分别在针齿壳和输入轴的端面施加固定约束,在输出盘端面施加逆时针的额定扭矩T.

表4 材料参数Tab.4 Parameters of materials
3 扭转刚度特性
3.1 仿真结果
由初始位置开始,对应曲柄轴回转 1周,等间距地选取100个测点,分别构建整机的有限元模型.对应每一个模型导入相应的轴承刚度值,设置啮合齿数为 5并确定啮合针齿号.分别计算每一个模型的扭转刚度,可得该减速器整机扭转刚度随曲柄轴转角变化的曲线,如图8所示.
由图 8可见,整机扭转刚度在曲柄轴转角为 0°和180°附近取到峰值,在曲柄轴转角为120°和240°附近时分别取到谷值.峰值位置对应曲柄轴 1的偏心方向垂直于曲柄轴孔 1中心与摆线轮中心的连线方向;两个谷值位置分别对应曲柄轴2和3的偏心方向,与相应的轴孔与摆线轮中心的连线垂直.
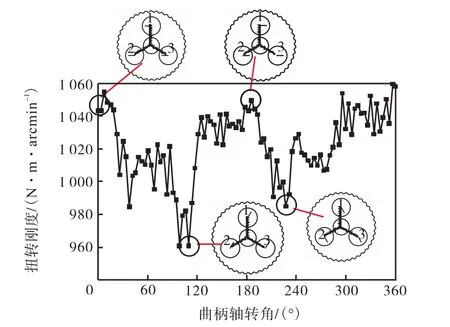
图8 扭转刚度随曲柄轴转角变化Fig.8 Variation of torsional stiffness with angle of crank shaft
还可以看出,该减速器扭转刚度的算术平均值为1029.46 N⋅ m⋅ ar cmin−1,波动幅值为99.54 N⋅ m⋅arcmin−1,波动幅值占刚度平均值的9.67%.
3.2 与实验结果比较
为验证整机扭转刚度有限元分析的正确性,以某公司所生产的同型号 RV减速器为对象搭建扭转刚度实验台,测试了该减速器的扭转刚度,并与仿真结果进行了对比研究.
实验采用固定输入端,在输出端加载,并测量输出端转角的刚度测试方案,测试实验台如图 9所示.该实验台主要是由激光干涉仪、扭矩加载装置、RV减速器、分度头等主要装置组成.其中分度头用于锁定输入轴以及调整输入轴转角,螺旋千斤顶与力传感器结合实现扭矩的加载,激光干涉仪用于测量输出端转角.

图9 RV减速器扭转刚度实验台Fig.9 Torsional stiffness experimental table of RV reducer
实验测试采样点与仿真模型一致.仿真结果与实验测试结果的比较如图10所示.
从图 10可见,整机扭转刚度的仿真结果整体上略高于实测结果.这与建模中忽略输出盘支撑轴承刚度及零部件装配弹性等因素有关.
整机扭转刚度的实验结果与仿真结果的最大相对偏差约为 10%,算术平均值的偏差约 5%.从拟合曲线中也可看出,两种情况下的曲线趋势相同,具有共同的扭转刚度特性.
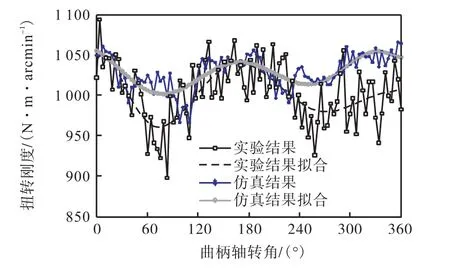
图10 仿真与实验结果比较Fig.10 Comparison between simulation and experimental results
4 影响因素分析
4.1 轴承刚度的影响
首先,将轴承设为刚体,忽略轴承刚度的影响,计算可得该减速器的扭转刚度随曲柄轴转角的变化曲线,如图11(a)所示.
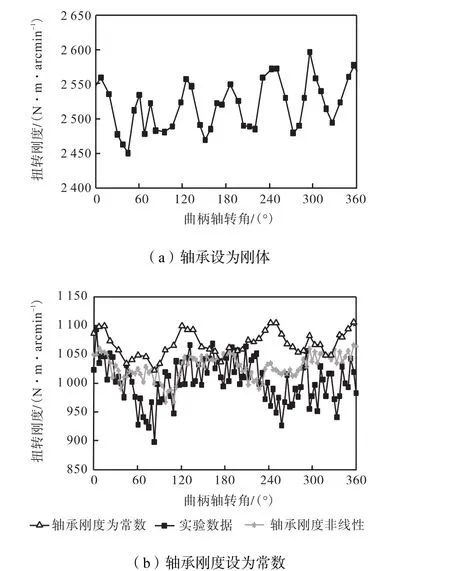
图11 轴承刚度对扭转刚度的影响Fig.11 Effect of bearing stiffness on torsional stiffness
对比图8可见,扭转刚度曲线的趋势发生了明显的变化.一方面,扭转刚度的算术平均值由原来的1029.46 N⋅ m⋅ arcmin−1变为 2519.70 N⋅ m⋅ ar cmin−1;另一方面,扭转刚度随曲柄轴转角的变化曲线趋于平缓.因此可知,轴承刚度决定着减速器平均扭转刚度的大小及变化趋势.由此可得,轴承刚度是决定该类减速器扭转刚度大小的决定性因素,也是造成该减速器刚度波动的关键环节.
为进一步探讨轴承刚度随载荷呈非线性的变化特性对整机扭转刚度的影响,对应曲柄轴的任意旋转位置,将轴承刚度设为图4中各轴承刚度的算术平均值,计算该减速器的扭转刚度,并与第 3.1节、第 3.2节中仿真与实验结果对比,结果如图11(b)所示.
由图 11(b)可以看出,忽略轴承刚度随载荷的非线性变化因素后,整机扭转刚度均值略有提高,但是刚度曲线的趋势发生了明显的变化.与实验结果相比较,考虑了轴承刚度非线性因素的情况下,仿真曲线更接近实验曲线.这说明刚度曲线的变化幅值与轴承刚度的非线性特征直接相关.因此,仅将轴承刚度设置为常数值的分析模型是不够精确的.
4.2 啮合刚度的影响
摆线轮与针齿之间的啮合刚度是整机扭转刚度的重要组成部分.为探究该项刚度的影响规律,首先将摆线轮与针齿设为刚体,其余构件设为弹性体,得该减速器扭转刚度曲线如图12(a)所示.
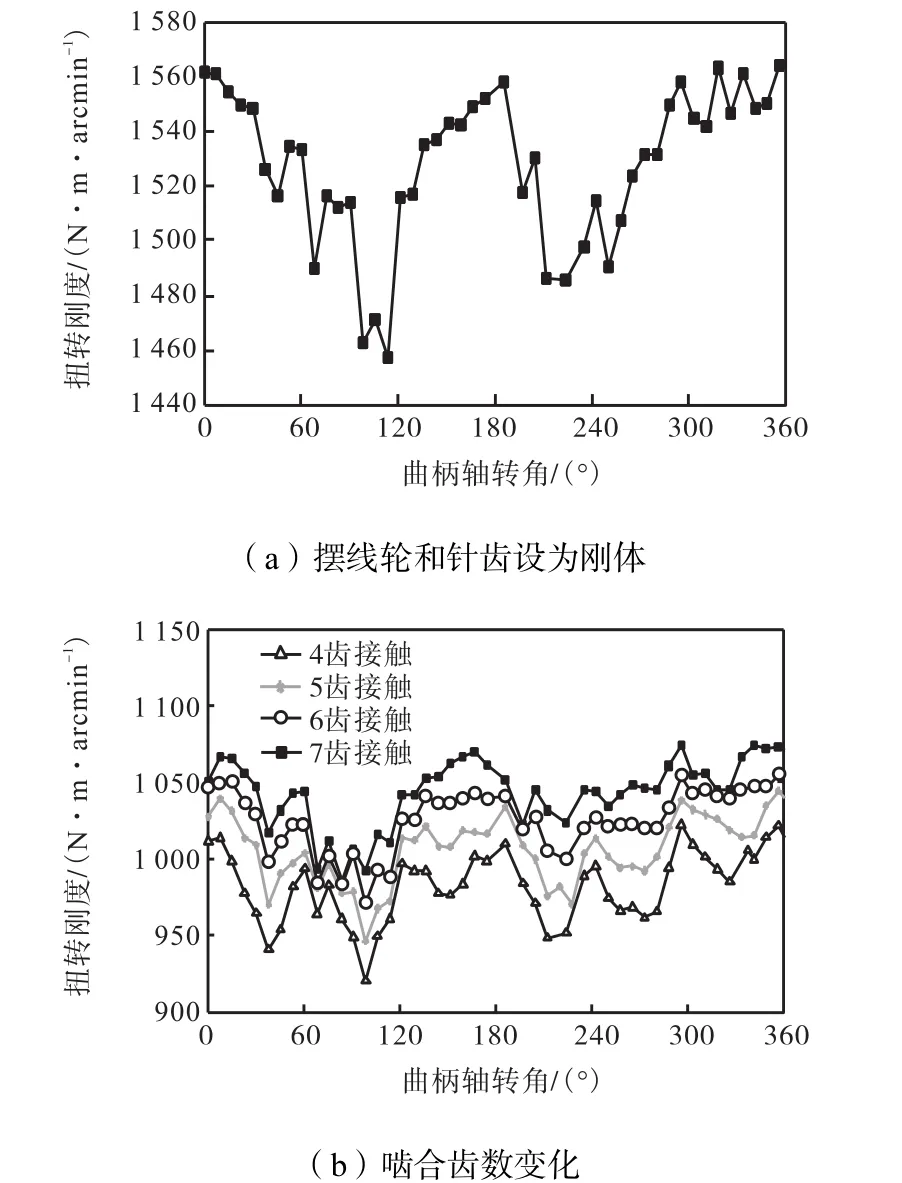
图12 啮合刚度对扭转刚度的影响Fig.12 Effect of meshing stiffness on torsional stiffness
为进一步研究摆线轮与针齿间的啮合齿数对扭转刚度的影响规律,将摆线轮与针齿间的啮合齿数分别设为 4、5、6、7,计算不同啮合齿数下整机扭转刚度,结果如图12(b)所示.
对比图 12(a)与图 8可知,在忽略啮合刚度时,整机扭转刚度的整体趋势同样未发生明显变化,但是扭转刚度的算术平均值明显增大,增大幅度为48.61%.因此啮合刚度是影响整机扭转刚度的主要因素,但不影响扭转刚度的波动.
由图 12(b)可以看出,在不同的啮合齿数下,扭转刚度曲线变化趋势相同,且啮合齿数越多,刚度越大.但是,随着啮合齿数的增大,扭转刚度增大的幅度略有减小.因此可得,啮合齿数仅影响整体扭转刚度平均数值的大小.
5 结 论
(1)轴承刚度是影响整机扭转刚度的主要因素.将轴承刚度视为随载荷非线性变化时能更精确地揭示整机的扭转刚度特性,较将轴承刚度视为常数值时更接近实验测试结果.
(2)摆线轮与针齿的啮合齿数是影响整机扭转刚度平均数值的主要因素之一,但对扭转刚度的变化趋势影响不大.
(3)对应曲柄轴自转 1周,整机扭转刚度在曲柄轴转角为 0°与 180°附近取得扭转刚度的最大值,在120°与240°附近取得最小值.
[1] Liu Jingya,Matsumura Shigeki,Chen Bingkui,et al. Torsional stiffness calculation of double-enveloping cycloid drive[J]. Journal of Advanced Mechanical Design,2012,6(1):2-14.
[2] Zhang Xiuyan,Dai Xiaojun. Meshing stiffness analysis of four ring-plate-type pin-cycloid gear planetary drive [J]. Applied Mechanics and Materials,2012,229/230/ 231:499-502.
[3] 张大卫,王 刚,黄 田,等. RV减速机动力学建模与结构参数分析[J]. 机械工程学报,2001,37(1):69-74. Zhang Dawei,Wang Gang,Huang Tian,et al. Dynamic formulation of RV reducer and analysis of structural parameters[J]. Chinese Journal of Mechanical Engineering,2001,37(1):69-74(in Chinese).
[4] 张迎辉,肖君君,何卫东. 机器人用 RV减速器针摆传动啮合刚度计算[J]. 大连交通大学学报,2010,31(2):20-23. Zhang Yinghui,Xiao Junjun,He Weidong. Meshing rigidity calculation of pin-cycloid on robot RV reducer[J]. Journal of Dalian Jiaotong University,2010,31(2):20-23(in Chinese).
[5] Park J S. Stiffness and Error Analysis of the Cycloid Drive[D]. Korea:College of Engineering,Seoul National University,2006.
[6] Kim Kyoung-Hong,Lee Chun-Se,Ahn Hyeong-Joon. Torsional rigidity of a cycloid drive considering finite bearing and hertz contact stiffness[C]// Proceedings of the ASME 2009 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. San Diego,California,USA,2009:1-6.
[7] Guo Yi,Parker R G. Stiffness matrix calculation of rolling element bearings using a finite element/contact mechanics model[J]. Mechanism and Machine Theory,2012,51:32-45.
[8] 董向阳,邓建一,陈建平. RV传动机构的受力分析[J]. 上海交通大学学报,1996,30(5):65-70. Dong Xiangyang,Deng Jianyi,Chen Jianping. Force analysis of RV transmission mechanism[J]. Journal of Shanghai Jiaotong University,1996,30(5):65-70(in Chinese).
[9] Meng Yunhong,Wu Changlin,Ling Liping. Mathematical modeling of the transmission performance of 2KH pin cycloid planetary mechanism[J]. Mechanism and Machine Theory,2006,42(7):776-790.
[10] 王 刚,郭茂林. 航天航空滚动轴承刚度[J]. 哈尔滨工业大学学报,2001,33(5):644-650. Wang Gang,Guo Maolin. Stiffness of aerospace rolling bearings[J]. Journal of Harbin Institute of Technology,2001,33(5):644-650(in Chinese).
[11] 李力行. 摆线针轮行星传动的齿形修正与受力分析[J]. 机械工程学报,1986,22(l):40-49. Li Lixing. The modification manner for tooth profile and the analysis of forces on the cycloid disk of a cycloid speed reducer[J]. Chinese Journal of Mechanical Engineering,1986,22(1):40-49(in Chinese).
[12] 孙 宇. 摆线针轮行星减速器的有限元分析研究[D].杨凌:西北农林科技大学机械与电子工程学院,2008. Sun Yu. Finite Element Analysis for Cycloid Pin Gear Planetary Reducer[D]. Yangling:College of Mechanical and Electronic Engineering,Northwest A & F University,2008(in Chinese).
(责任编辑:金顺爱)
Analysis of the Characteristics of Torsional Stiffness of RV Reducer
Yang Yuhu,Zhu Linyu,Chen Zhenyu,Shen Zhaoguang
(Key Laboratory of Mechanism Theory and Equipment Design of Ministry of Education,Tianjin University,Tianjin 300072,China)
The RV reducer,which is widely used in the robot joint,was studies as the research object. The geometric model is constructed based on the structural features of RV reducer,and the FEA model is also established considering bearing stiffness,meshing stiffness of gears,and elasticity of components on the platform of ANSYS. The variation of torsional stiffness,which is generated in a period of rotation of the crank shaft,is compared with the experimental results in order to certify the validity and computational accuracy of the model. By applying this FEA model,the effect of bearing stiffness and the mating tooth number between cycloidal gear and pin gear is further analyzed. The result indicates that the bearing stiffness is the dominant factor that affects the torsional stiffness. Considering the nonlinear variation of the bearing stiffness can reveal the characteristics of torsional stiffness more precisely.
RV reducer;torsional stiffness;bearing stiffness;meshing stiffness
TH132.414
A
0493-2137(2015)02-0111-08
10.11784/tdxbz201309096
2013-09-25;
2013-11-28.
国家高技术研究发展计划(863计划)资助项目(2011AA04A102).
杨玉虎(1962— ),男,博士,教授.
杨玉虎,yangyuhu@tju.edu.cn.
时间:2014-02-28. 网络出版地址:http://www.cnki.net/kcms/detail/12.1127.N.20140228.1310.003.html.
