基于移动传感器网络的气体源定位
2015-05-10吴玉秀孟庆浩
吴玉秀,孟庆浩,曾 明
(天津大学电气与自动化工程学院机器人与自主系统研究所,天津 300072)
基于移动传感器网络的气体源定位
吴玉秀,孟庆浩,曾 明
(天津大学电气与自动化工程学院机器人与自主系统研究所,天津 300072)
针对目前基于无线传感器网络定位气体源方法中存在的因探索区域尺寸、边界等先验知识缺失而造成节点部署困难的问题,提出了一种使用有限个低成本机器人构成移动传感器网络进行气体源定位的方法.该方法中,首先以期望拓扑结构排列的移动传感器网络节点采集气体浓度并上传至上位机;然后上位机使用非线性最小二乘方法对气体源位置进行估计,并将位置估计结果发送给移动传感器网络节点;最后由移动节点计算出目标位姿,并采用饱和控制的方法镇定到该位姿.通过上述步骤的不断循环,移动传感器网络最终将移动到气体源附近,从而实现对气体源较为精确的定位.室内自然通风环境中,使用 6个自制的机器人组成具有固定圆形拓扑的移动传感器网络进行了气体源定位实验.实验结果表明,适当选择拓扑半径,该方法可在 6,min左右实现精度为 30,cm的气体源定位.
移动传感器网络;气体源定位;非线性最小二乘;动态部署
在很多行业中,需要使用危险化学品.这些危险化学品(特别是气体)一旦泄漏将直接对人的生命和财产造成威胁.目前,使用无线传感器网络(wireless sensor network,WSN)的气体源定位(gas source localization,GSL)的研究取得了较大的进展[1-3].然而,在使用WSN对气体源进行定位的过程中,通常需要节点的部署覆盖到气体源;另外,为保证对气体源定位的精度,在距离气体源较近的位置必须部署节点.因此在实际情况下(特别是在未知环境中),主要靠增大传感器散布的面积和密度来满足以上两点.这也是目前采用WSN解决GSL的多数研究停留在仿真阶段的主要原因.
考虑WSN在GSL应用中的局限性,利用多机器人对气体扩散形成的烟羽进行跟踪,进而实现对气体源定位的研究已得到了一些研究者的重视. Zarzhitsky等[4]利用多机器人编队,使用通量趋向性算法实现了烟羽跟踪和释放源定位.Hayes等[5]提出了一种协调 spiral-surge(S-S)方法,该方法利用处于上风向且当前为surge状态的机器人吸引处于下风向的机器人或者当前处于spiral状态的上风向的机器人.这些方法都需要实时对测得的风信息和测得的气体浓度信息进行处理,根据输出的信息直接控制机器人进行运动.另外,一些学者使用优化的方法对气味源进行定位.文献[6-7]对粒子群优化(particle swarm optimization,PSO)算法进行改进并应用于气体源定位.骆德汉等[8]利用机器人测得浓度信息,改进了蚁群优化(ant colony optimization,ACO)算法使其适用于多机器人多气味/气体源定位.优化算法在烟羽搜索上应用具有很大的优势,但由于随机运动的存在,需机器人频繁运动,特别是针对现实中气体浓度的间歇性和离散性,更增加了搜索的难度.故在文献[6]中使用风信息来优化随机搜索的方向.综上所述,由于现有的风传感器或者比较昂贵,或者功耗较大,或者体积较大,且由于低成本的微(小)机器人的运行速度和能量受到限制,故上述算法较难在实际中实现.
综合WSN和多机器人GSL方法,本文提出了一种基于移动传感器网络(MSN)的气体源定位算法,所提定位算法中移动节点不需对风信息进行实时测量.该算法可以看作是一个通过有限节点的传感器网络的动态部署实现对气体源进行估计的过程.每个估计周期分两步,首先对环境中的气体进行一段时间的测量,根据测量的浓度均值对气体源位置参数进行估计;接着在朝向估计值的方向上选择一点作为网络的几何中心重新部署网络.
在对气体源参数估计时,文中采用最小二乘的方法;节点的重新部署对单个机器人而言相当于机器人在指定位置实现点镇定,笔者使用饱和控制的方法来实现.
此外,在自然通风的室内环境中,使用自制的MSNN对本文方法的有效性进行了实验验证,并与相同环境下的WSN的定位方法进行了对比,证明本文方法具有一定的优势.
1 问题描述
使用有限数量的机器人作为移动节点组成具有固定几何拓扑结构的 MSN对气体源进行定位的方法结合了WSN和移动机器人两方面的优势,可以实现从较远的距离不断移动并接近气体源,最终实现对气体源的定位.
图 1给出了使用 MSN对气体源进行定位的实现方案.图中的定位过程可以描述为:首先,在气体烟羽覆盖的范围内,给定MSN的几何拓扑和拓扑基准点( ),使机器人按照给定的拓扑排列;其次,所有机器人对浓度值进行测量,把测量值上传到上位计算机,计算机利用接收的值对源的位置 (,进行估计得到 (,),然后把该估计值广播给每个机器人;再次,机器人以接收到的源位置估计值),在保持原几何拓扑不变的情况下,通过计算得到自己的目标点,进而获得期望的镇定位姿;反复进行上述估计运动过程,直到源位置估计值 ()收敛,实现对气体源的定位.
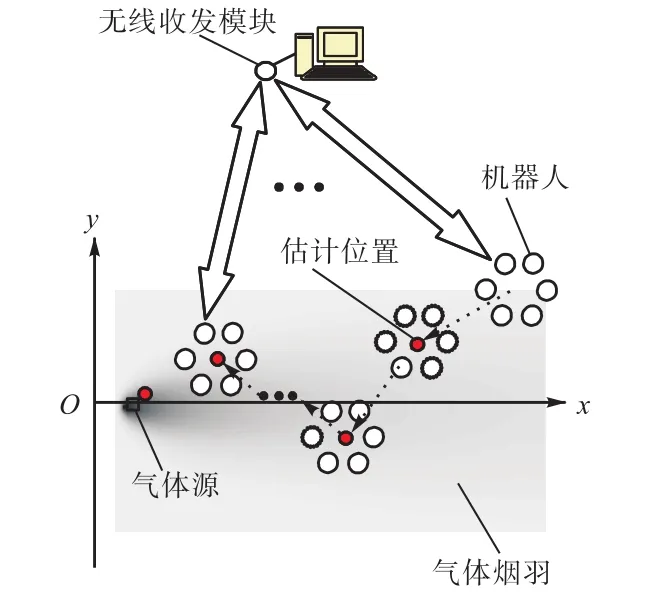
图1 基于MSN的气体源定位方案Fig.1 Scheme of gas source localization based on MSN
2 气体扩散模型与传感器标定
采用由多个机器人组成的 MSN对气体源进行定位时,首先需要知道气体在测量范围内的扩散模型;其次,在定位区域中平均风速已知的前提下,机载气体传感器测得的浓度信息是定位过程中所利用的主要信息.对同一浓度值,测量所用机器人能够得到较为相近甚至相同的值,才能保证浓度测量的有效性.故而,气体扩散模型的确定和传感器的标定是定位算法实现的前提条件.
2.1 气体扩散模型
Jones[9]通过实验证明采用类高斯模型所得出的浓度分布与实测浓度相吻合.故而在时均风恒定(即风的波动较小),且风的湍动具有各向同性和均匀性的条件下,令平均风向的下风向为x轴正方向,则根据文献[10]可以得到二维气体扩散的高斯模型为
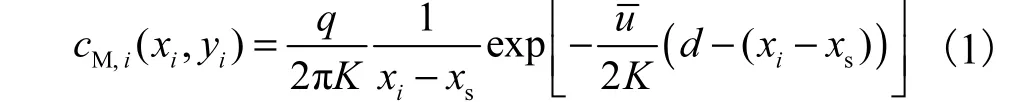
式中:cM,i(xi, yi)为通过模型计算得到的坐标点(xi, yi)的浓度值;q为气体的平均释放率;K为湍流扩散系数;为风速的均值;d为点(xi, yi)与气体源的 (xs, ys)的距离,
图 2给出了使用式(1)计算出的浓度分布,图中气体源位于(30,cm,0,cm),平均风速设置为10,cm/s,释放率和湍流扩散系数分别为 30,mL/h和30,cm2/s.
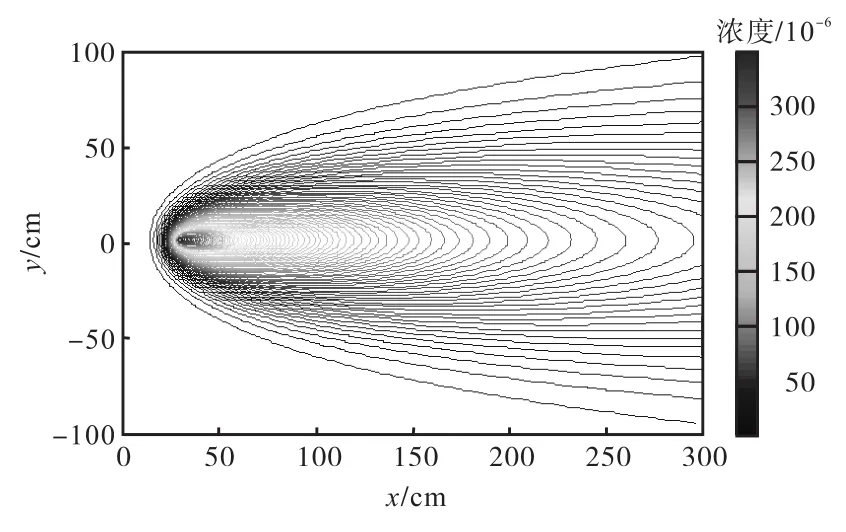
图2 类高斯扩散模型下的气体浓度分布Fig.2 Gas concentration distribution using Gaussian-like diffusion model
2.2 气体传感器标定
本研究中,使用酒精蒸气作为目标气体,机载气体传感器采用 e2v公司的金属氧化物半导体传感器MICS-5521,此类传感器的电阻值会随目标气体浓度的增加而减小,其电路连接方式见图3[11].
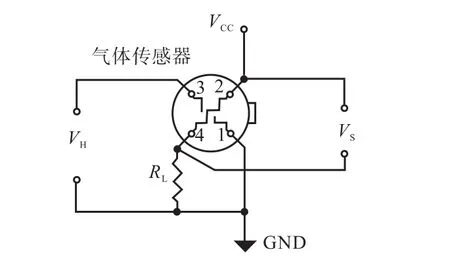
图3 气体传感器MICS-5521电路Fig.3 Circuit of the gas sensor MICS-5521
图 3中sV表示气体传感器的输出.多次实验表明,环境的温度和湿度对传感器的电压输出sV影响比较明显,但是对sV的变化值sVΔ (气体传感器当前电压与其在纯净空气中电压的差值)的影响较小,所以此处使用气体浓度c和对应的输出电压变化值sVΔ对传感器进行标定.类似于文献[12]中公式,此处有

式中1α、2α和3α为待定参数,对于不同的传感器它们的值不同.实际标定过程中,根据已知浓度值和与之对应的 ΔVs,使用非线性拟合的方法得到待定的参数值.
3 基于MSN的气体源定位
处于气体烟羽当中固定几何拓扑的 MSN,根据其移动节点机载气体传感器的测量值,利用非线性最小二乘的方法估计气体源的位置,然后驱使移动节点使用饱和控制的方法镇定到新的位姿,且保证所有节点镇定后传感器网络的几何拓扑中心是气体源的估计位置,且拓扑中心不变.这是气体源定位过程中的主要步骤.上述两个步骤不断循环,即可使 MSN部署到气体源附近,实现对气体源位置较为精确的定位.
3.1 气体源位置估计
使用多个空间位置不同的移动节点测得的浓度数据对气体源位置进行估计,使用的是MSN中的传感器网络的特点,此处采用非线性最小二乘法来实现.非线性最小二乘法是一种参数估计方法[13],其基本原理是选择模型中要估计的参数,使得利用该参数和已知非线性模型计算出的函数值与测量值之间误差的平方和最小,应用此方法的原因是该方法不需要浓度测量误差的先验知识,并且其数值求解容易实现.
针对本文的问题,MSN中的n个机器人对环境中的气体浓度进行测量,机器人i的测量值为 cR,i,并通过无线通信模块上传到上位计算机.令 (ˆ,)表示气体源的估计位置,结合式(1)的高斯模型,可得非线性最小二乘的目标函数为
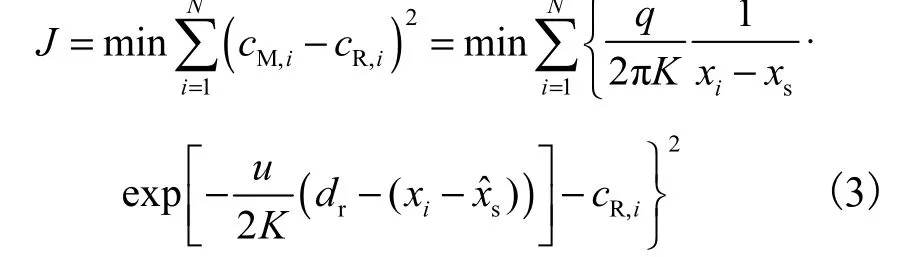
式中 dr为机器人i的位置与估计的气体源位置之间的距离
在上述最小二乘问题中,( xˆs, yˆs)为待估参数.笔者使用文献[14]中的迭代算法对上述的非线性最小二乘问题进行求解得到 (ˆ,).
3.2 MSNN镇定
MSNN镇定是指 MSNN可以运动到指定的位姿,这是节点能够进行重新部署的关键.本研究中采用自行设计与研发的差速驱动小型移动机器人(multi-robot for intelligent cooperative exploration,MICE)作为MSNN(见图4),则其运动学方程为

式中:(xc, yc,θ)为机器人的位姿;ν和ω分别为机器人的线速度和角速度.

图4 MICE机器人及机载传感器Fig.4 MICE robot and onboard sensors
设计上述机器人的控制器,通常需要考虑约束
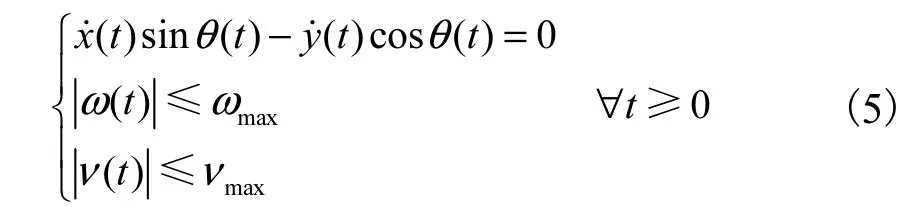
根据文献[15]中的方法,定义坐标变换
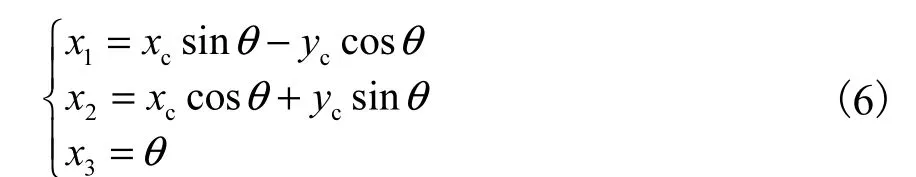
基于式(4)的 MSNN模型,设计了一种无源、光滑的饱和时变控制器

式中 ρ1、ρ2和 ρ3为待定参数,由文献[15]中的命题 1中的结论可知:在给定νmax和 ωmax的限定下,适当调整式(7)所示的控制器中的参数 ρ1、ρ2和 ρ3可使机器人从任意位姿 (x, y, θ)T全局渐近收敛到 (0, 0, 0)T.
在实际应用过程中,移动节点i需要从起点位姿P=(x ,y,θ)T镇定到期望位姿 P=(x,y,θ)T.
b,i b,i b,i b,i e,i e,i e,i e,i由于控制器位于机器人上,要使用控制器(7)控制机器人完成 Pb→Pe的运动,需要把期望位姿看作是系统的平衡点(0, 0, 0).令 ΔPbe,i=(Δ xbe,i, Δ ybe,i, Δ θbe,i)T表示期望位姿相对于初始位姿的相对位姿,则有从而输入控制器的初始位姿为
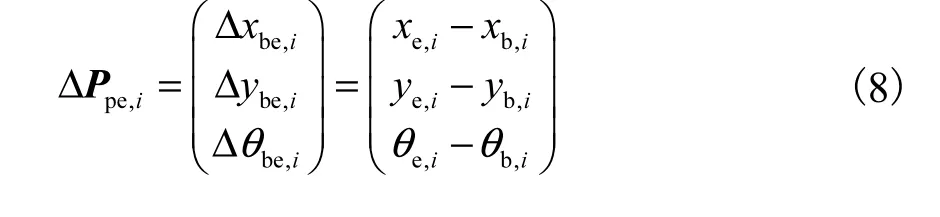
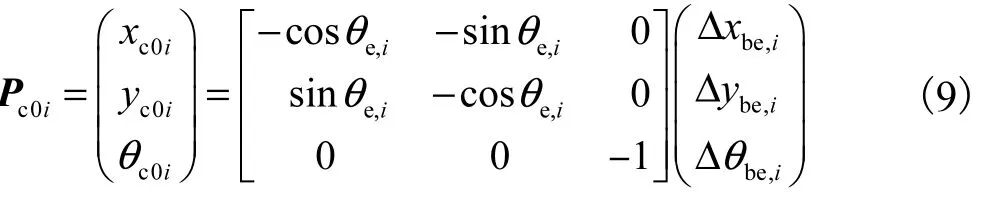
证明:根据文献[15]中的命题1,可知机器人可以从任意的位置全局渐近收敛到位姿 (0, 0, 0)T,然后结合式(8)和式(9),显然推论1的结论成立.
3.3 MSNN目标位姿确定及运动同步
在本文中,令MSN的拓扑结构固定,且MSNN在起始位置按照固定拓扑排列,且全部朝向平均风向的反方向.在估计过程中,假设一段时间内的平均风速/风向不存在大的波动,根据图 4所示的气体传感器的安装位置,则 MSNN始终朝向与平均风向相反的方向更有利于浓度测量.故而 MSNN期望朝向不变即 Δ θbe= 2k π(k = 0,1,2,? ).上一定位周期气体源估计位置为 (x ˆs0,y ˆs0);当前估计周期气体源估计位置为(xˆs, yˆs),则移动传感器节点i期望位姿为

在 MSNN镇定过程中,由于其采用相同的镇定算法,联合式(9)和式(10)可知
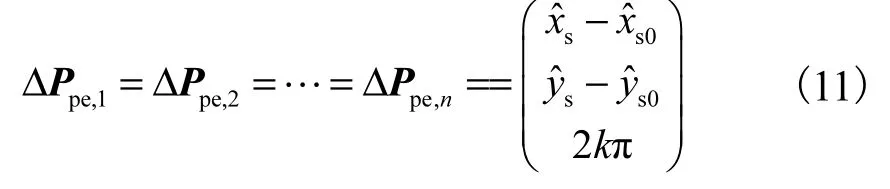
在运动过程中,MSNN之间的拓扑保持不变,且均使用控制器(7)进行控制.故只要保持机器人起始点同步,且整个地面环境差异较小的情况下,MSNN之间不会发生碰撞.所以在环境中不存在除 MSNN之外的其他障碍物时,MSNN运动过程中不考虑避障.
在每个MSN的定位周期,机器人于镇定之前都需要上位机发一个字节的同步信号,使得环境中的所有MSNN同时开始运动,即可实现运动同步.
3.4 气体源定位算法
结合上述的气体源位置预估和 MSNN镇定方法,配合上位机与MSNN之间的通信,可以实现基于MSN的气体源定位算法.算法流程见图5.算法实现步骤如下.

图5 基于MSN的气体源定位算法流程Fig.5 Flow chart of gas source localization using MSN
步骤2 在指定位置实现镇定的MSNN每隔一定的时间 tΔ采集一次所在位置的浓度值,并通过无线模块上传至上位机.
步骤 3 上位机每隔时间MT对每个节点收集的数据进行去野和平均处理,得出时间间隔MT内的统计浓度值.
步骤4 判断接收数据是否合理.合理则应用非线性最小二乘法求解式(3)中的目标函数,得出估计点 (xˆs, yˆs);否则放弃这次估计,重新采集数据.判断数据合理的标准是:存在至少2个传感器浓度测量值检测到气体.
步骤 6 判断是否满足停止条件,停止条件为:MSN中存在 TM内测量浓度值的波动量大于阈值 cf的 MSNN,且 2次估计值之间距离小于固定阈值ε.当停止条件满足,停止.
步骤 7 不满足停止条件,上位机向 MSNN发送估计结果,然后延时 2tc(tc为 MSNN控制周期)等待.
步骤 8 ,MSNN接收到上位机传来的数据,利用式(11)计算期望位姿,等待运动同步信号.
步骤9 上位机发送运动同步信号,MSNN接收到运动同步信号,应用控制器(7)镇定到期望位姿.转到步骤2进行新一轮的估计.
为了对实验结果进行评价,定义MSN拓扑基点(xs0,ys0)移动的总距离大于λ,估计结果还不能满足停止条件,则估计失败,其中λ选择为搜索区域外接圆的直径.
4 实验与分析
4.1 实验设置
实验在图6所示的室内自然通风的环境中进行,选取环境中通风方向上3,m×3,m的正方形区域为实验区域.

图6 实验环境示意Fig.6 Sketch of the experimental environment
实验中使用6台自制的如图4所示的MICE机器人,机器人上装有气体传感器、电子罗盘、无线通信模块以及用于机器人之间相对定位的麦克风和蜂鸣器.MICE机器人采用两轮差速控制,机器人的最大线速度 νmax= 0.4m/s,机器人最大角速度为ωmax= 11.52rad/s.机器人本体没有安装风速/风向传感器.
实验所用气体源如图7所示,图中所示通过调速真空泵和质量流量控制器可以控制气流的输出速度,只要控制锥形瓶中的酒精浓度,就可以达到控制释放率的目的.如图7所示,采用恒温水浴箱改变锥形瓶中的温度控制酒精的蒸发速度来控制酒精的浓度.在本文的实验中,释放率和湍流扩散系数分别为30,mL/h和30,cm2/s.

图7 气体源Fig.7 Gas source
图 8所示为实验区域中心位置放置的一台超声风速仪在480,s内所测的风速(相对于实验区域坐标系的)和风向.求得风速和风向的均值分别为12.45 cm/s和0.36°,标准差分别为3.72,cm和19.53°.
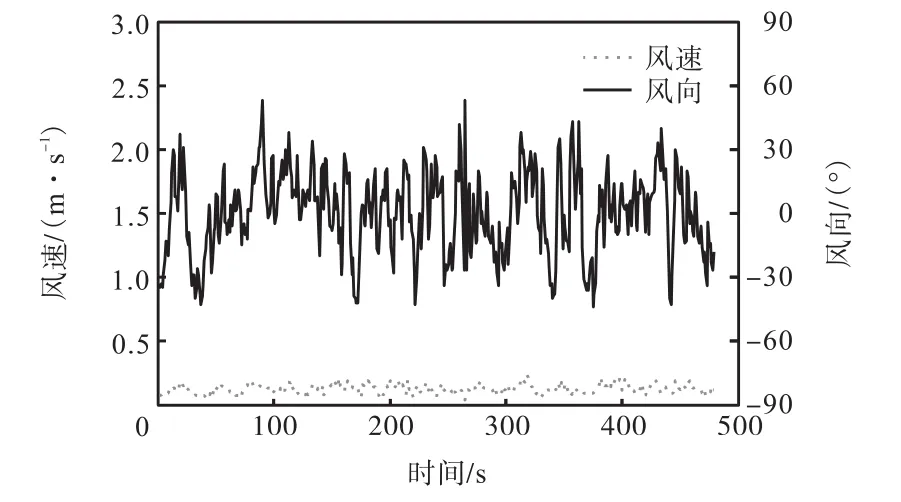
图8 用超声风速仪测量的风速和风向信号Fig.8 Wind magnitude and direction measured by using an ultrasonic anemometer
实验中使用第2.2节所述的方法对10支传感器进行标定,选取其中参数相近的 6支安装到机器人上.图 9给出其中一个传感器标定过程中,拟合的ΔVs与浓度值c之间关系曲线,对应参数为

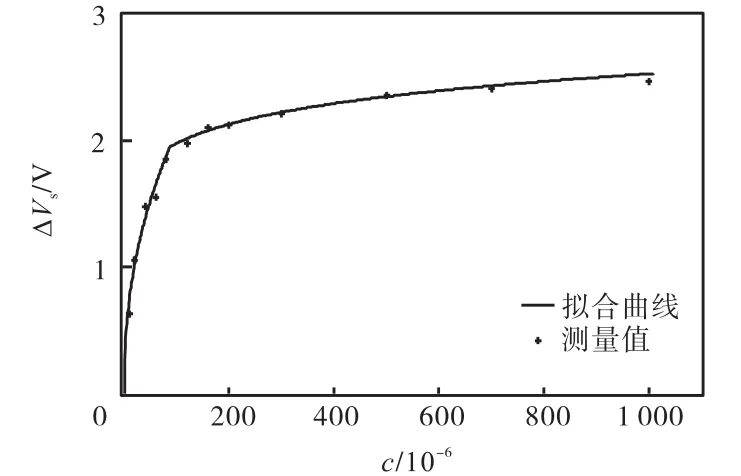
图9 气体传感器标定过程中的拟合曲线Fig.9 Fitted curve in the gas sensor calibration process
实验中由 6个小型机器人组成的 MSN的几何拓扑为圆形,第3.4节中所涉及参数设置如下.
在没有气体释放时,标定好的传感器测量的浓度值上下波动幅度在2×10-6以下,故在实际实验中当测量得到的浓度值不小于 2×10-6时,定义 MSNN可检测到目标气体.
TM的选择与传感器的响应恢复曲线有关.据测试得知MICS-5521传感器的响应加恢复时间在10,s左右,故而此处为了采集浓度的波动信号,TM的采集时间不小于10,s,此处选择 TM=30,s.
把MSN移动到气体源附近,对气体源的估计值大部分能落在30,cm的范围内,故选择 ε= 30 cm.且此时 MSN中的存在浓度的波动值达到 100×10-6的MSNN,故选择 cf=100×10-6.
针对第 3.2节中的 MSNN镇定,选择参数ρ1= 0.4,ρ2= 0.3,ρ3= 0.2.则可保证≤ωmax,≤νmax.
4.2 实验结果
为了确定现实实验中的MSN的几何拓扑半径,首先对本文的算法进行了仿真.考虑到 MICE机器人的体积,MSN拓扑半径从 30,cm~100,cm每隔10,cm进行了50次仿真,结果如下.
(1) 当拓扑半径选择为30,cm时,气体源定位成功率为 98%,通常完成定位需要 9或 10个定位周期;平均估计误差为53,cm.
(2) 当拓扑的几何半径选择为60,cm时,仅仅需要 6或 7个定位周期即可完成估计,平均估计误差24.97,cm,成功率为70%.
(3) 当拓扑半径选择在70,cm~100,cm之间时,需要 6~7个定位周期可以完成估计,定位的成功率降低到50%以下.
鉴于如上的仿真结果,分别选择MSN的拓扑半径 30r= cm和 60r= cm进行了实验.实验过程中,浓度的采集周期 0.5tΔ= s,定位周期 60T= s,MSNN的控制周期为c0.5t= s.
利用第 4.1节中设置的控制参数,结合式(7)给出的控制器,进行大量的仿真和实验.结果表明,在x≤ 2.4m,y ≤ 2.4m的范围内,当式(10)中的k取值为 1,则机器人可以在 30,s内镇定到任意点(x, y, 2π),令镇定误差表示为(εx,εy,εθ),则有≤ 5cm,≤ 10cm,≤2°.
图10(a)和10(b)分别给出了仿真机器人轨迹与MICE实际运行轨迹以及仿真机器人朝向变化与MICE实际运行过程中朝向变化.从图中可以看出,MICE实际运行的路径与仿真轨迹有较小偏差.并且实验过程中角度的收敛速度略高于仿真结果且 30,s能收敛到 2°以内.实现了从(0 m, 0 m, 2π rad)到(2.4 m, 2.4 m, 0 rad)的镇定,镇定误差为 (1.1cm,10 cm,1.89)°.根据第3.4节中所述,机器人每次移动距离小于2r,故MSNN在一个定位周期移动的最大距离小于等于 2×60=120,cm,所以此处的镇定效果能满足要求.
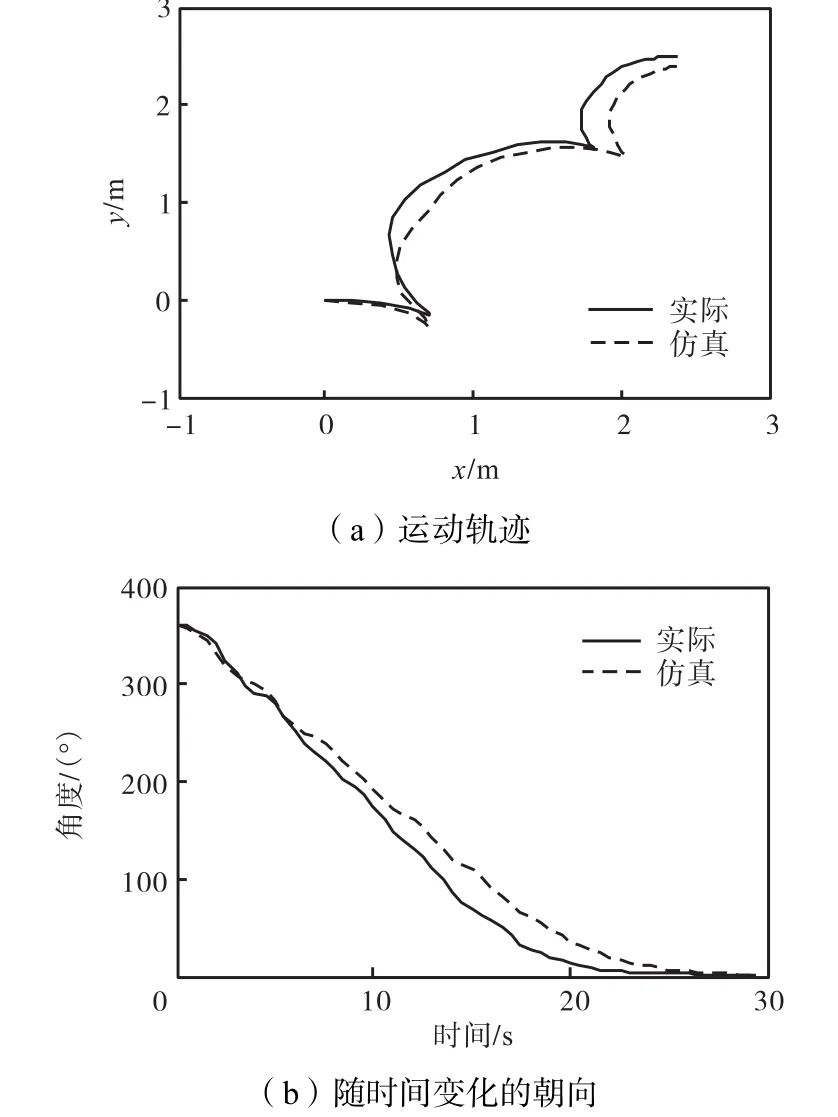
图10 镇定过程(初始位姿(0, 0, 2π),目标位姿(2.4, 2.4, 0))Fig.10 Stabilization process(starting from(0, 0, 2π)to (2.4, 2.4, 0))
图11给出了r=30,cm时使用6个MSNN成功定位气体源的实验过程中的几个瞬间截图.整个定位过程中,初始点为 P0(2 .1m, - 0.90 m),气体源位P1(1.80 m,- 0.86 m)→ P2(1.46m, - 0.74m)→ P3(1.25 m, -0 .40 m)→ P4(0.74 m,-0 .18 m)→ P5(0.17 m,-0.34 m)→ P6(0.32m,-0 .10m).此过程中的浓度统计值见表1(详细的实验过程录像见链接 http://v.youku.com/ v_show/id_XNjA2MDY0ODA0.html).
表 2给出了实验的结果,其中γ为定位成功率;Ttotal为定位成功需要的估计周期平均值;L为成功定位的 MSN中心点移动的直线距离之和的平均值;E为定位成功的平均误差.
根据表 2给出的实验结果可以看出,实验中,当r=60,cm 时,实验中的定位误差明显大于仿真中的误差.这主要是由于在气体源附近,烟羽呈细条状,MSN靠近气体源时,由于拓扑半径比较大,很多情况下只有一个传感器能够测得有效的浓度值.这样,另外一个传感器的干扰信号很容易引起对气体源位置的误估,增大估计误差.

图11 使用MSN定位气体源场景Fig.11 Scenario of gas source localization using MSN
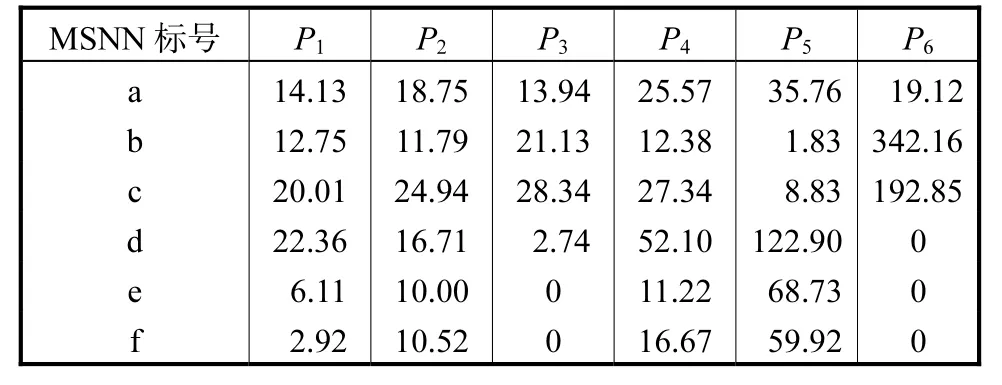
表1 对应图11气体源定位过程中MSNN浓度统计值Tab.1 Concentration statistics of MSNN in gas sourcelocalization process corresponding to Fig.11 10-6

表2 基于MSN的气体源定位结果Tab.2 Results of gas source localization using MSN
为了说明本文所提MSN方法相对于固定WSN的优势,进行了固定 WSN的实验.保持上述 MSN实验中的条件不变,使用非线性最小二乘方法,进行了20次定位实验.每次定位实验中,WSN节点的位置是由随机函数产生的0~3的不重合的6个二维随机向量.根据表2中对Ttotal的定义,此处每次定位实验进行10次单独的估计,且估计周期选择与MSN相同,选定10次估计的平均值作为最后的结果.
使用基于WSN的气体源定位算法的最后20次的平均估计误差为 64.53,cm,明显高于使用本文MSN方法的估计误差.另外使用 WSN进行气体源定位的过程中,其估计误差波动强烈.
5 结 语
本文提出了一种适用于室内自然通风条件下的使用移动传感器网络对气体泄漏源进行定位的方法.实测风数据和实验结果表明,该方法的实现不需要严格规定风是恒定不变的假设.若给 MICE配备避障模块,则文中方法可用于简单的结构化环境(如大型仓库、实验室、油库等)中进行危险气体源泄漏的定位.另外,文中对文献[15]中的饱和控制器进行了推广,并且通过对初始角度的选择,使得其在有限时间内可以实现一定范围内任意点的镇定.实验表明具有较小的误差,这保证了移动节点动态部署的准确性.
[1] Zhao F,Shin J,Reich J. Information-driven dynamic sensor collaboration for tracking applications [J]. IEEE Signal Processing Magazine,2002,19(3):61-72.
[2] Vijayakumaran S,Levinbook Y,Wong T F. Maximum likelihood localization of a diffusive point source using binary observations [J]. IEEE Transactions on Signal Processing,2007,55(2):665-676.
[3] 匡兴红,邵惠鹤. 基于传感器网络的气体源定位方法研究 [J]. 系统仿真学报,2007,19(7):1464-1467. Kuang Xinghong,Shao Huihe. Study of plume localization based on WSN [J]. Journal of System Simulation,2007,19(7):1464-1467(in Chinese).
[4] Zarzhitsky D,Spears D. Swarm approach to chemical source localization [C]// IEEE International Conference on Systems,Man and Cybernetics. Waikoloa:IEEE Press,2005:1435-1440.
[5] Hayes A T,Martinoli A,Goodman R M. Distributed odor source localization [J]. Sensors Journal,IEEE,2002,2(3):260-271.
[6] Meng Q H,Yang W X,Wang Y,et al. Collective odor source estimation and search in time-variant airflow environments using mobile robots [J]. Sensors,2011,11(11):10415-10443.
[7] 张建化,巩敦卫,张 勇. 基于微粒群优化的有限通信多机器人气味寻源 [J]. 控制与决策,2013,28(5):726-730. Zhang Jianhua,Gong Dunwei,Zhang Yong. Localizing odor sources using multiple robots based on particle swarm optimization in limited communication environments[J]. Control and Decision,2013,28(5):726-730 (in Chinese).
[8] 骆德汉,邹宇华,庄家俊. 基于修正蚁群算法的多机器人气味源定位策略研究 [J]. 机器人,2008,30(6):536-541. Luo Dehan,Zou Yuhua,Zhuang Jiajun. Multi-robot odor source localization strategy based on a modified ant colony algorithm[J]. Robot,2008,30(6):536-541 (in Chinese).
[9] Jones C. On the structure of instantaneous plumes in the atmosphere [J]. Journal of Hazardous Materials,1983,7(2):87-112.
[10] Ishida H,Kagawa Y,Nakamoto T,et al. Odor-source localization in the clean room by an autonomous mobile sensing system[J]. Sensors and Actuators B:Chemical,1996,33(1/2/3):115-121.
[11] E2V Company. MiCS-5521 Datasheet [R]. A1AMiCS5521 Version 2,2008.
[12] Graf M,Barrettino D,Taschini S,et al. Metal oxidebased monolithic complementary metal oxide semiconductor gas sensor microsystem [J]. Analytical Chemistry,2004,76(15):4437-4445.
[13] Kay S M. Fundamentals of Statistical Signal Processing,VolumeⅠ: Estimation Theory[M]. Upper Saddle River:Prentice Hall,1993.
[14] Coleman T F,Li Y. An interior trust region approach for nonlinear minimization subject to bounds [J]. SIAM Journal on Optimization,1996,6(2):418-445.
[15] Jiang Z P,Lefeber E,Nijmeijer H. Saturated stabilization and tracking of a nonholonomic mobile robot [J]. Systems & Control Letters,2001,42(5):327-332.
(责任编辑:孙立华)
Gas Source Localization Based on Mobile Sensor Network
Wu Yuxiu,Meng Qinghao,Zeng Ming
(Institute of Robotics and Autonomous System,School of Electrical Engineering and Automation,Tianjin University,Tianjin 300072,China)
Considering the difficulty in deploying the nodes for the wireless-sensor-network-based gas source localization(GSL)methods owing to the lack of the prior knowledge such as the detecting area and the boundary,this paper addresses a GSL method using the mobile sensor network(MSN)which is composed of a limited number of low-cost robots. In this method,firstly,the MSN nodes with expected topology collect gas concentration and send it to a central node;Secondly,the central node estimates the gas source location using a nonlinear least square method and sends the outcome to the MSN nodes;Finaly,the MSN nodes calculate the target pose and the nodes are stabilized near the target using saturation control. Through repeating the above cycles,the MSN nodes can eventually approach the gas source. Experiments in an indoor ventilated environment show that a GSL accuracy of 30 cm within about six minutes could be achieved.
mobile sensor network;gas source localization;nonlinear least squares;dynamic deployment
TP391
A
0493-2137(2015)02-0139-08
10.11784/tdxbz201309028
2013-09-07;
2013-10-11.
国家自然科学基金资助项目(61271321,60875053);教育部博士点基金资助项目(20120032110068).
吴玉秀(1982— ),男,博士研究生,yuxiu_wu@163.com.
孟庆浩,qh_meng@tju.edu.cn.
时间:2013-11-08. 网络出版地址:http://www.cnki.net/kcms/detail/12.1127.N.20131108.1045.002.html.
