三孔中心圆直径测量方法
2015-05-09广东省佛山市南海诚志齿轮厂528222许一帆
金属加工(冷加工) 2015年4期
广东省佛山市南海诚志齿轮厂 (528222) 许一帆
带有圆心落在同一个圆上的三孔孔组结构零件(见图1)如法兰、端盖和行星架等,由于中心圆是个虚拟圆,不能直接测量,通常要使用三坐标测量机或投影仪,但这些测量设备不适于生产现场做快速检测,且有点儿大材小用。为此,笔者研究出一种更简单有效的检测方法。
1. 测量原理
用直线将三个孔的中心连接起来,就构成一个三角形,而中心圆正是这个三角形的外接圆(见图2)。只要量出孔与孔的中心距a、b和c,就能求出中心圆的直径D。这样一来,测量中心圆直径的问题,就简化为测量孔间中心距的问题。而孔间中心距用简单的量具就可以轻易测出。
2. 中心圆直径求解
测得三个孔间中心距后,可以通过下面两种方法求出中心圆的直径。
(1)作图法:使用制图软件,以三个中心距a、b和c为边作三角形,然后通过三个顶点作出三角形的外接圆,便可以通过标注这个圆的直径尺寸,求得中心圆的直径。
(2)计算法:根据三角形余弦定理和正弦定理,先用余弦定理求得其中一角α,然后用正弦定理算出外接圆即中心圆的直径D=a/sinα。
第一种方法简单直接,但需要使用制图软件;第二种方法只要用科学型计算器就可以求得答案,但操作步骤多,容易发生错误。另外,这两种方法均要求检验人员有一定的数学知识,而且求解步骤仍然较多,不够快速方便。为了解决上述弊端,根据第二种方法的算法,编写了一个小程序(见图3),只需将三个中心距输入相应的文本框,点击按钮,即可得出中心圆的直径。
3. 结语
经比较,应用这种检测方法的检测结果与其他检测方法的相差不大,证明该方法是准确有效的,而且操作简便。应用上述小程序,省去了求解过程,大大提高了工作效率。
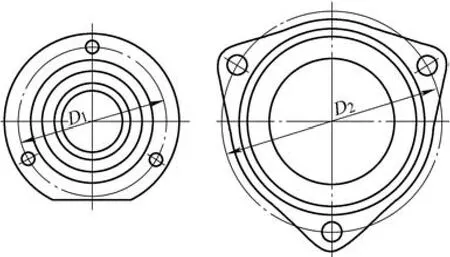
图 1
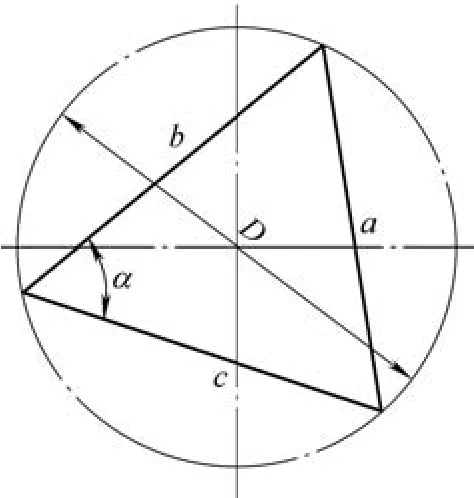
图 2
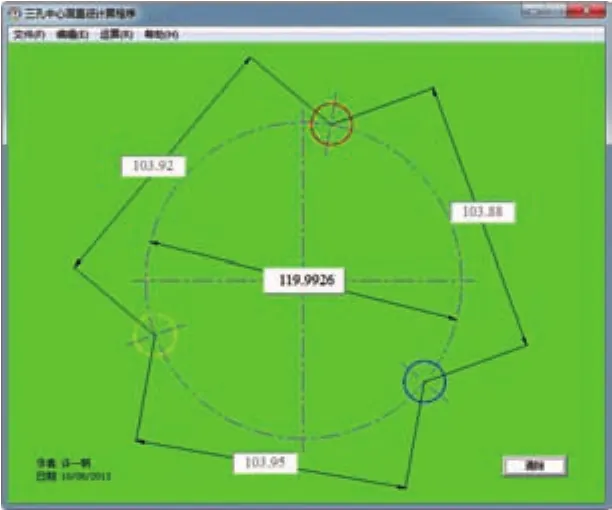
图 3
