考虑地下水作用的Goodman-Bray方法改进及应用
2015-05-09高连通晏鄂川谢良甫
高连通,晏鄂川,谢良甫
(中国地质大学(武汉) 工程学院,武汉 430074)
考虑地下水作用的Goodman-Bray方法改进及应用
高连通,晏鄂川,谢良甫
(中国地质大学(武汉) 工程学院,武汉 430074)
反倾岩质边坡的稳定性分析方法一般为Goodman-Bray法,但其没有考虑地下水。对Goodman-Bray法进行改进,推导出了考虑地下水作用的反倾岩质边坡稳定性计算方法,并用MATLAB编写了计算程序。最后以重庆巫溪县中梁水库硝洞槽—郑家大沟反倾岩质边坡为例,采用Sarma法和传递系数法(TCM)对改进的Goodman-Bray法(简称WGB法)进行验证。结果表明:反倾岩质边坡往往受自身岩体结构的控制,条块划分结合结构面产状的Sarma法和WGB法比铅直方向条分的TCM法更符合实际情况,但Sarma法忽视了对条块底面连通性的考虑,使计算结果偏低。综合比较3种计算方法,WGB法更加适用于考虑地下水作用的库岸反倾岩质边坡稳定性分析。
Goodman-Bray法;反倾岩质边坡;WGB法;传递系数法;Sarma法;稳定性分析
1 研究背景
倾倒破坏是反倾岩质边坡失稳的主要模式,常发生于走向与边坡大致平行但倾向相反的层状岩体中,当岩体中发育有顺坡向的节理或裂隙时边坡倾倒破坏更容易发生。在国内外的水利水电、矿山、铁路、城市环境灾害等方面都出现过大量反倾向边坡失稳破坏的灾难性事故,然而这种广泛存在的反倾向岩体边坡的工程地质问题在20世纪60年代初才逐步被人们认识到和加以研究[1]。
目前国内外关于反倾岩质边坡稳定性评价方法可归纳为解析分析法、数值模拟和物理模拟3大类。谭儒蛟等[1]、邹丽芳等[2]就国内外反倾岩体边坡变形机制与规律认识,以及稳定性评价方法的研究进展进行了系统总结。在这些评价方法中,极限平衡分析法仍然是目前最常用的一种方法。Goodman-Bray[3-4]最早提出了分析倾倒稳定的极限平衡法,该方法将滑坡体用反倾向的结构面切割成n个宽度为ΔL的矩形条块,对于任一条块,作用在其上的力将使该条块处于稳定、倾倒破坏和滑动3种状态中的一种。Goodman-Bray法虽然很简便,非常方便在工程实际中应用,但该法还存在着一些局限性,比如假定岩柱底滑面完全连通会使得计算结果过于保守;另外离散条块的底面与侧面正交,这并非一般的实际情况。针对这些局限性,国外Bobet[5],Aydan and Kowamoto[6],Wylie[7]等对这一方法做出了改进,国内陈祖煜等[8]、汪小刚等[9]还对其数学模型做了改进,并推导出了不考虑地下水作用改进的Goodman-Bray法,其考虑了底面和侧面不正交的一般情况,计入了节理岩体的连通率,使用Sarma法[10]建议的临界加速度法重新定义了安全系数,并优化了最可能的破坏模式。此外在数值模拟方面,蔡跃等[11]根据不连续体理论,利用离散元软件UDEC,模拟倾倒破坏行为,并讨论了影响边坡稳定性的各种因素。尹锡杰等[12]应用FLAC3D研究某反倾页岩边坡应力、应变等值线及相应增量等值线图确定边坡潜在最危险滑动面和次级滑动面,并计算了其稳定性系数。徐佩华等[13]采用FLAC3D软件计算和分析不同蓄水位下的边坡稳定性,得到较理想的结果。
目前常用于反倾岩质边坡的稳定性分析方法为Goodman-Bray法,但其没有考虑地下水,而在库岸反倾岩质边坡的倾倒变形破坏形成过程中,地下水位随库水位周期性的升降变化,从而不断地改变边坡岩体内的渗流场,导致边坡岩体内的应力状态不断调整,加速边坡的倾倒变形破坏。为此本文对Goodman-Bray法进行改进,推导出了考虑地下水作用的反倾岩质边坡稳定性计算方法,并用MATLAB编写了计算程序。最后以重庆巫溪县中梁水库硝洞槽-郑家大沟反倾岩质边坡为例,采用Sarma法和传递系数法对改进的Goodman-Bray法(简称“WGB”法)进行验证。
2 考虑地下水作用的Goodman-Bray法
2.1 模型建立
WGB法计算如图1所示,条块编号从坡脚向上编,Ns和Nt分别为最后一个滑动块体和最后一个倾倒块体编号,图中虚线表示某一计算时刻的稳定地下水位线。

图1 WGB法计算示意图Fig.1 Schematic diagram of the calculation by improved Goodman-Bray method in consideration of groundwater effect
2.2 公式推导
WGB法中,首先计算边坡达到极限平衡状态时的临界加速度系数η,通过迭代最终获得安全系数Fs。具体步骤如下。
2.2.1 条块力的递推公式
在进行条块力的递推时,对于某一条块,根据力的平衡条件,计算侧面作用力的方程可以表达成下面的一般形式,即
Pr=APl+B+ηC。
(1)
式中:Pr,Pl分别为右侧面和左侧面作用力;A,B,C为系数,分别通过滑动块和倾倒块的平衡方程求得(具体推导过程不做详述,可参考文献[14])。
(1) 对于滑动岩柱,其受力分析如图2所示。A,B,C为系数,计算公式见式(2)至式(5)。
(2)
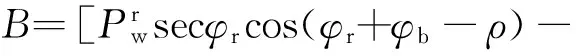
(3)

图2 滑动块体岩柱受力分析
Fig.2 Forces on a sliding block
(4)
K=cos(φr+φb-ρ)secφr。
(5)
(2) 对于倾倒岩柱,其受力分析如图3所示。计算公式见式(6)至式(9)。
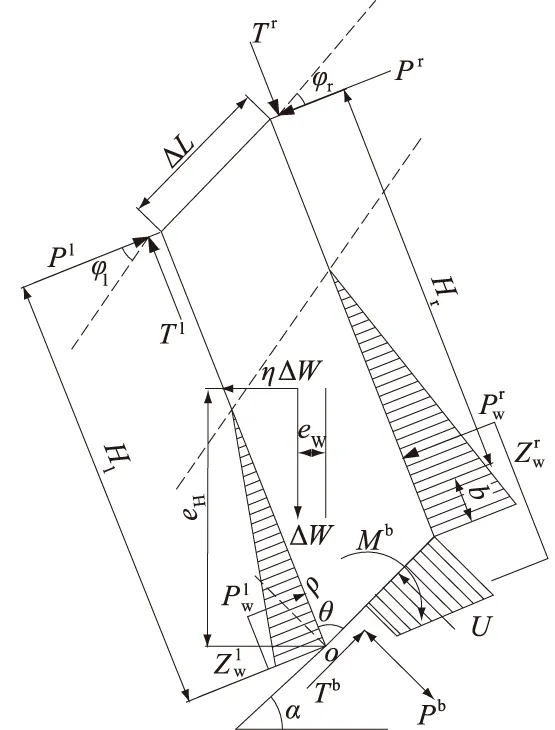
图3 倾倒块体岩柱受力分析
Fig.3 Forces on a toppling block
(6)
(7)

(8)
K=Hr+b+ΔLsinρ+
(9)

2.2.2 计算η的公式
对于第i块岩柱,有
Pr,i=AiPl,i+Bi+ηCi;
(10)
式(10)也可表达为
Pr,i=Fi+ηGi。
(11)
令
Fi=AiPl,i+Bi;
(12)
Gi=Ci。
(13)
由于
Pl,i=Pr,i-1=Fi-1+ηGi-1;
(14)
将式(14)代入式(10)可得:
Fi=AiFi-1+Bi;
(15)
Gi=AiGi-1+Ci。
(16)
设Nt为最后一个倾倒块编号,则
Pr,Nt=FNt+ηGNt=0 。
(17)
故有
(18)
2.3 计算步骤
WGB法计算步骤如下:
(1) 假定一个Fs值,得
(2) 选定一个Ns和Nt,根据式(18)计算η。
(3) 不断变化Ns和Nt,最终找到相应最小的η的Ns和Nt。这样就同时确定了破坏模式和相应的η值。
(4) 不断变化Fs,获得相应的η,最终获得相应η=0时的Fs,即为最终的稳定性系数值。
3 Sarma法和传递系数法简介
3.1 Sarma法
Sarma法[10]是Sarma博士于1979年提出的,是一种考虑滑体强度的边坡极限平衡方法。Sarma法采用斜条分法,假定条块倾斜界面之间也达到了极限平衡,这样静力平衡方程和未知数的数目恰好匹配,也就是说求解安全系数可变成静定的问题。由于岩体内通常都存在着一组陡倾角的结构面,在发生滑动破坏时,一方面沿底滑面滑动,一方面也沿这些陡倾角结构面错动,因此,Sarma法是一个分析岩质边坡稳定较合理的方法。Sarma法力学模型如图4所示。

图4 Sarma法力学模型Fig.4 Mechanics model of Sarma Method
3.2 传递系数法
传递系数法(TransferringCoefficientMethod,以下简称“TCM法”)适用于滑动面为折线形的滑坡。它主要假定条块间的作用力合力方向与滑动面倾角一致,滑动面的破坏服从Mohr-Coulomb破坏准则。传递系数法沿整个滑动面满足静力的平衡条件,但不满足力矩平衡条件。TCM法力学模型如图5所示。

图5 传递系数法力学模型Fig.5 Mechanics model of TCM
4 工程实例分析
4.1 岸坡概况
硝洞槽—郑家大沟岸坡位于重庆市巫溪县中梁一级电站(中梁水库)坝址上游1.2km处,岸坡研究区地处亚热带湿润区,属中低山峡谷岩溶地貌单元。岸坡总体地势呈南高北低,岸坡体中前部地势较陡,后部地势相对较缓,岸坡体冲沟发育(见图6(a));研究区出露地层(见图6(b))主要为第四系全新统残破积层(Q4el+dl)、第四系全新统崩坡积层(Q4col+dl)、三叠系下统嘉陵江组(T1j)、三叠系下统大冶组(T1d),岸坡岩层薄—中厚层状,岩层反倾;研究区内发育2组优势节理:(306°~350°)∠(45°~70°)和(50°~80°)∠(50°~88°)。研究区水文地质条件较为简单,地下水的主要补给来源是大气降水及地表水。所处的地质环境导致硝洞槽—郑家大沟岸坡形成了弯曲倾倒变形体(见图6(c)),在外界因素影响下,坡体易发生整体或局部变形破坏。

图7 3种方法计算模型Fig.7 Calculation models of three methods

图6 岸坡研究区地质图Fig.6 Geological conditions of the rock slope area
4.2 计算模型建立
模型建立的时候,由于实际岸坡中前部(高程860m以下)的变形较大,将中前部重新建立模型单独求解,图7为整体岸坡计算模型,考虑地下水作用改进的Goodman-Bray法(以下简称“WGB法”)计算模型条块采用平行四边形划分;Sarma法计算模型条块采用不规则四边形划分;TCM法计算模型条块采用两边铅直的不规则四边形划分。
4.3 计算工况及计算参数
根据中梁水库的蓄水设计特征,本次稳定性计算将4种不同蓄水水位高程作为4种计算工况,分别为:① 530m(未蓄水);② 590m(死水位);③ 613m(溢洪道水位底高程);④ 625m(正常蓄水)。
根据岸坡勘察报告,结合当地工程经验值,确定岸坡岩体及结构面的力学参数如表1、表2所示。

表1 岩土体物理力学参数Table 1 Physical and mechanical parametersof rock and soil

表2 节理及层面力学参数Table 2 Mechanics parameters of joint and bedding plane
4.4 计算结果
根据各种方法的计算公式,采用MATLAB高性能数值计算功能编写相应的计算程序代码,将从AutoCAD导出的各个条块坐标点数据,读入预定程序,即可计算出不同模型不同工况下的稳定系数,计算结果见表3所示。
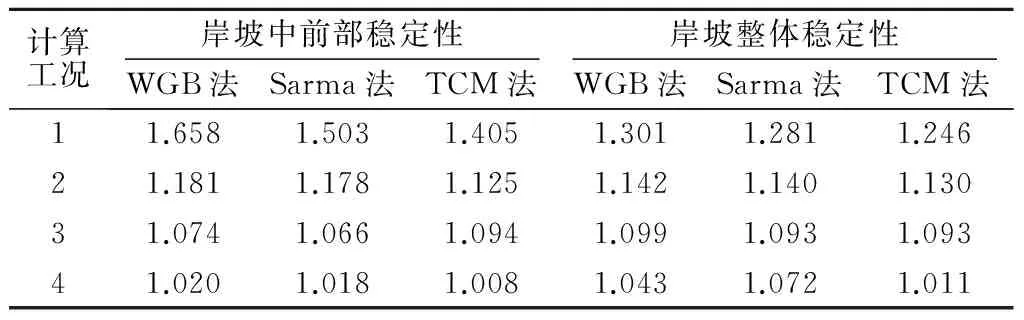
表3 岸坡稳定性计算结果Table 3 Calculation results of slope stability
从表3中可以看出,3种计算方法得到的稳定性变化趋势一致:在水库未蓄水工况下,中前部岸坡稳定性明显大于岸坡整体稳定性;在水库不同蓄水水位时,岸坡整体及中前部稳定性均下降,且中前部稳定性下降程度明显大于整体稳定性下降程度,表明中前部岸坡受库水位影响作用明显;水位低于613 m时岸坡中前部稳定性大于岸坡整体稳定性,而当水位高于613 m之后,岸坡整体稳定性大于中前部的稳定性,这说明在水位低于613 m时,该岸坡稳定性大小主要由原有岸坡结构特征控制,而在水位高于613 m之后,岸坡稳定性受水库蓄水作用影响明显,实质上是原有岸坡弯曲倾倒折断面在一定区域产生蠕滑形成滑动面的表现。
对比表3中3种算法的计算结果可以看出:WGB法由于考虑了滑动面的连通率而使计算结果偏高;Sarma法由于考虑了条块侧面的极限状态而使计算结果较不考虑条块侧面作用力的TCM法高,但却低于WGB法的计算结果;3种算法都考虑了地下水的作用,相较于实际情况,层状反倾岩质边坡本身受岩体结构面控制,WGB法和Sarma法由于考虑条块侧面作用力而优于TCM法;此外,基于结构面的产状划分平行四边形条块(WGB法)和不规则四边形条块(Sarma法)比铅直划分条块(TCM法)更能真实再现层状反倾岩质边坡的实际情况。
5 结 语
(1) WGB法计算得到的稳定性系数与Sarma法和TCM法计算得到的稳定性系数变化趋势一致,说明考虑地下水作用的改进Goodman-Bray法可以作为评价反倾岩质边坡稳定性评价的一种解析法。
(2) 反倾岩质边坡往往受自身岩体结构的控制,条块划分结合结构面产状的Sarma法和WGB法比铅直方向条分的TCM法更符合实际情况,但Sarma法忽视了对条块底面连通性的考虑,使计算结果偏低。综合比较3种计算方法,WGB法更加适用于考虑地下水作用的库岸反倾岩质边坡稳定性分析。
[1] 谭儒蛟,杨旭朝,胡瑞林.反倾岩体边坡变形机制与稳定性评价研究综述[J].岩土力学,2009,30(增刊2):479-484,623. (TAN Ru-jiao, YANG Xu-zhao, HU Rui-lin. Review of Deformation Mechanism and Stability Analysis of Anti-dipped Rock Slopes[J]. Rock and Soil Mechanics, 2009, 30 (Sup.2):479-484,623.(in Chinese))
[2] 邹丽芳,徐卫亚,宁 宇,等.反倾层状岩质边坡倾倒变形破坏机理综述[J].长江科学院院报,2009,26(5):25-30. (ZOU Li-fang, XU Wei-ya, NING Yu,etal. Overview of Toppling Failure Mechanism of Countertendency Layered Rock Slopes[J]. Journal of Yangtze River Scientific Research Institute, 2009, 26(5): 25-30. (in Chinese))
[3] GOODMAN R E, BRAY J W. Toppling of Slopes[C]∥Proceedings of the Specialty Conference on Rock Engineering for Foundations and Slopes ASCE/Boulder. Geotechnical Engineering Division of ASCE. Colorado, August 15-18, 1976: 201-243.
[4] BRAY J W, GOODMAN R E. The Theory of Base Friction Models[J]. International Journal of Rock Mechanics and Mining Sciences and Geo-mechanics Abstract,1981, 18(6): 453-468.
[5] BOBET A. Analytical Solutions for Toppling Failure[J]. International Journal of Rock Mechanics and Mining Sciences, 1999, 36(7):971-980.
[6] AYDAN O, KAWAMOTO T. The Stability of Slopes and Underground Opening Against Flexural Toppling and Their Stabilization[J]. Rock Mechanics and Rock Engineering, 1992, 25(3):143-165.
[7] WYLLIE D C. Toppling Rock Slopes Failures: Examples of Analysis and Stabilization[J]. Journal of Geotechnical Engineering, ASCE, 1983,109(8): 1039 -1062.
[8] 陈祖煜,张建红,汪小刚.岩石边坡倾倒破坏稳定分析简化方法[J]. 岩土工程学报,1996,18(6):92-95. (CHEN Zu-yu, ZHANG Jian-hong, WANG Xiao-gang. Simplified Method of Rock Slope Stability Analysis of Toppling Failure [J]. Chinese Journal of Rock Mechanics and Engineering, 1996, 18(6): 92-95. (in Chinese))
[9] 汪小刚,贾志欣,陈祖煜.岩石边坡倾倒破坏的稳定分析方法[J].水利学报,1996,(3):7-21. (WANG Xiao-gang, JIA Zhi-xin, CHEN Zu-yu. The Research of Stability Analysis of Toppling Failure of Jointed Rock Slopes [J]. Journal of Hydraulic Engineering, 1996, (3): 7-21. (in Chinese))
[10]SARMA S K. Stability Analysis of Embankments and Slopes [J]. Journal of Geotechnical Engineering Division, 1979, 28(3):346-349.
[11]蔡 跃,三谷泰浩,江琦哲郎.反倾层状岩体边坡稳定性的数值分析[J]. 岩石力学与工程学报, 2008, 27(12):2517-2522. (CAI Yue,YASUHIRO M, TETSURO E. Numerical Analysis of Stability for an Ant-dip Stratified Rock Slope [J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27 (12):2517-2522. (in Chinese))
[12]尹锡杰,晏鄂川,孙兆来.某反倾页岩边坡破坏面确定及其稳定性分析[J]. 岩土力学,2007,28(增刊):595-598. (YIN Xi-jie, YAN E-chuan, SUN Zhao-lai. Slip Surface Ascertaining and Stability Analyzing of the Countertendency Shale Slope[J]. Rock and Soil Mechanics, 2007 , 28 (Sup.): 595-598. (in Chinese))
[13]徐佩华,陈剑平,黄润秋,等.某水电站解放沟左岸反倾高边坡蓄水稳定性分析[J]. 岩土力学,2005,26(5):827-832. (XU Pei-hua, CHEN Jian-ping, HUANG Run-qiu,etal. Stability Analysis of Left High Slope at Jiefanggou under the Condition of Storing Water for a Certain Hydropower Station[J]. Rock and Soil Mechanics, 2005,26(5):827-832. (in Chinese))
[14]陈祖煜. 岩质边坡稳定分析——原理·方法·程序[M]. 北京:中国水利水电出版社,2005.(CHEN Zu-yu. Rock Slope Stability Analysis: Theory, Method, and Programs[M]. Beijing: China Water Power Press, 2005. (in Chinese))
(编辑:姜小兰)
Improved Goodman-Bray Method in Consideration of Groundwater Effect
GAO Lian-tong, YAN E-chuan, XIE Liang-fu
(Faculty of Engineering, China University of Geosciences, Wuhan 430074, China)
Goodman-Bray Method is commonly used in the stability analysis for toppling rock slope, but the effect of groundwater is not considered. In view of this, we made an improvement to the Goodman-Bray method by deducing the stability calculation of toppling rock slope in consideration of groundwater effect, and wrote calculation program by using MATLAB. With a toppling rock slope in Wuxi, Chongqing City as a case study, we verified this improved Goodman-Bray method using Sarma Method and Transferring Coefficient Method (TCM) for comparison. Results suggest that the improved Goodman-Bray method and Sarma Method which combines rock block and structural planes could better reflect the practical situation than TCM because of the limits of toppling rock mass. But the connectivity of block bottom is neglected by using Sarma Method so that the calculation result is smaller than practice. So this improved Goodman-Bray method is more suitable to be used for stability analysis of toppling rock slope in consideration of groundwater effect.
Goodman-Bray Method; toppling rock slope; WGB method; Transferring Coefficient Method; Sarma Method; stability analysis
2013-09-15 ;
2013-10-31
国家重点基础研究发展计划(973)项目(2011CB710605)
高连通(1988 - ),男,云南宣威人,硕士研究生,主要从事岩土体稳定性评价与利用的研究,(电话)18086012268(电子信箱)gao-liantong@163.com。
晏鄂川(1969- ),男,四川内江人,教授,博士生导师,主要从事岩土体稳定性评价和防护设计以及灾害监测研究,(电话)027-67883507(电子信箱)yecyec6970@163.com。
10.3969/j.issn.1001-5485.2015.02.017
TU457
A
1001-5485(2015)02-0078-06
2015,32(02):78-83
