非饱和土渗透系数曲线的分段简化模型
2015-05-09王晓峰时红莲吴柳东
王晓峰,时红莲,王 震,吴柳东
(1.中国地质大学(武汉) 工程学院,武汉 430074; 2.山东正元建设工程有限责任公司,山东 烟台 264670)
非饱和土渗透系数曲线的分段简化模型
王晓峰1,2,时红莲1,王 震1,吴柳东1
(1.中国地质大学(武汉) 工程学院,武汉 430074; 2.山东正元建设工程有限责任公司,山东 烟台 264670)
根据影响非饱和土渗透系数变化的主要因素,选取合理特征点将土-水特征曲线划分成4个阶段。在此基础上,对大量数据进行统计分析,建立了一种分段简化模型,用于描述级配不良的非黏性土的非饱和渗透系数曲线,只需知道该模型中特征点的相关参数即可得到完整渗透系数曲线,并通过现有数据进行了验证分析。验证结果表明:在低基质吸力(0<ψ≤ψa)时,lnK-ψ曲线呈线性变化;而当θb<θ≤θa时,lnK-lnθ曲线也有类似变化规律。
非饱和土;渗透系数;分段简化模型;土-水特征曲线;基质吸力
1 研究背景
渗透系数是土的重要参数之一。在非饱和土中,由于受粒径大小、颗粒级配、孔隙分布、含水率、增(脱)湿路径、所处温度和压应力状态等众多因素的影响[1],渗透系数并不是一个常数。在近饱和状态下,吸力的微小变化也将引起渗透系数1至3个量级的变化[2],这使得直接实验测量难度变大、效率低下。除直接实验测试外,众多学者意图通过数学建模对渗透系数进行理论预测。目前,间接预测非饱和土渗透系数的模型可分为4类:经验模型、宏观模型、统计模型和分形模型。其中,统计模型[3]在岩土工程领域应用最广,其基本原理是在饱和渗透系数和土-水特征曲线(SWCC)已知的情况下,以孔隙分布函数作为中间函数推导出渗透系数曲线。
Childs等[4-6]开发了各自的孔隙分布函数模型。Marshall和Klute[7]全面分析了一些孔径分布模型并对其进行修正和改进。结合Young-Laplace方程再引入一个匹配系数得到了目前常用的渗透系数预测函数。
Van Genuchten[8]将建立的土-水特征曲线函数代入Burdine[9]与Mualem[10]提出的传导率模型中得出了封闭灵活的相对渗透系数Kr(ψ)表达式。该模型根据相应的土-水特征曲线和饱和渗透系数能确定出渗透系数函数。Fredlund等[11]结合Childs和Collis-George[4]提出的孔隙分布模型也获得了一个建立在整个土-水特征曲线上的渗透系数方程。
大多数研究人员采用“归一化”思路,设想用一个方程描述整个吸力范围内的渗透系数曲线,其共同的缺点是:预测结果不能完全适应整个吸力(含水率)范围,只是在某区间段上与实际结果吻合较好。这是因为,对于整个吸力范围,影响土体渗透系数变化的主导因素并不完全相同。由此,本文从影响液体流动因素的差异性入手,把完整土-水特征曲线划分为4段,并对大量数据统计分析验证分段的合理性,相应地给出了渗透系数分段简化表达式。
2 土-水特征曲线阶段划分
2.1 渗透系数影响因子
室温条件下,非饱和土体中流体的渗透系数与渗透流体的密度、动力黏度、材料固有渗透率以及一定含水率状态下对应的基质吸力有关,根据相关理论,它们之间的关系可用下式表示:
(1)
式中:K为渗透系数(m/s);ρ为流体密度(kg/m3);g为重力加速度(m/s2);μ为流体的动力黏度,与分子间作用力有关(N·s/m2);k为介质固有渗透率(m2);θ为土体含水率;ψ为与土体含水率对应的基质吸力(kPa);h(ψ),g(θ)为与土体吸力或含水率有关的函数。
假设在脱(吸)湿过程中对于同一种土D=ρgk为定值,则有:
(2)
综合考虑 ,θ和μ3个影响因子(其中ψ,θ存在一定的函数关系)将整个土-水特征曲线分成以下4个阶段:弯液面排水段,大、中孔隙排水段,微孔隙排水段和结合水膜段。
2.2 孔隙水分布模型与曲线分段
为分析基质吸力(或含水率)和流体的动力黏度对渗透系数的影响,首先给出非饱和土完整的土-水特征曲线经典模型(见图1)和持续脱湿过程中对应土-水特征曲线上各阶段土体内孔隙水与孔隙气的概念分布图(见图2)。

图1 土-水特征曲线(SWCC)示意图Fig.1 Sketch of SWCC for unsaturated soils
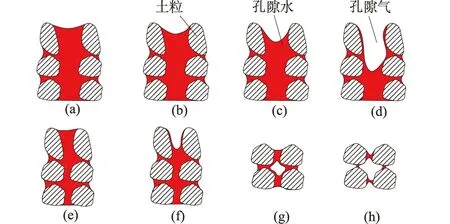
图2 持续排水条件下土体内孔隙水与孔隙气的概念分布Fig.2 Conceptual distributions of pore water and pore air in a cross-sectional area of rigid soil matrix during incremental drainage process
图2(a)对应图1中A′点,为饱和初始状态;图2(c)对应图1中的进气值A点,接触角达最小值;图2(e)对应图1中B点,大、中孔隙的排水基本结束,微小孔隙接触角不断减小;图2(g)对应图1中的C点,孔隙内排水终止,主要以结合水膜和蒸汽形式存在。A′点渗透系数可通过实测得到,记为Ks;A,B点对应的渗透系数分别记作Ka,Kb。
A点以前土体基质吸力的增加主要是因为接触角变小,排水通道弯液面下凹,使得土体内表面张力提供给基质吸力的分量值增大而导致,仅有少量水排出,对应图2(a)—2(c)的过程,将此阶段称为弯液面排水段。
到进气值A点时接触角达最小值,开始有气体进入直径较大的孔隙,通道内的水不断排出,A—B阶段吸力的增加主要是由含水率变化导致,对应图2(c)—2(e)的过程。此阶段因为通道直径较大,孔隙水的排出受结合水膜作用力的影响极小,故称之为大、中孔隙排水段。
到达B点时,土体内大、中孔隙的排水几乎终止,随着吸力的不断增加,微小孔隙开始排水,吸力继续增大,土体含水率越来越小,直到残余含水率C点,对应图2(e)—2(g)的过程。此阶段由于孔隙直径很小,孔隙内流动液体的每个质点距离强结合水膜的平均距离很小,其流动性受土体吸力和结合水膜作用力的共同影响,称之为微孔隙排水段。
需要说明的是B点对应的含水率并不是残余含水率,而是比残余含水率大,并且此值偏离残余含水率的程度与土体孔径分布和土颗粒表面结合水膜厚度有关,本文建议按图1所示方法确定,B′点即为B状态下对应的含水率。
低于C点时,孔隙水全部以结合水膜形式存在于粒间或附着于颗粒表面。土体内部流动的液体几乎完全受强结合水膜作用控制,这种电分子吸引力高达几千到几万个大气压且非常稳定,运移主要以蒸汽相为主,极少量以液相形式从结合水膜较厚的地方向结合水膜较薄的地方运移。由于这部分移动的孔隙水完全受颗粒表面强结合水膜作用力的控制,移动缓慢,且一般在常温下不能排出,表现为流体的动力黏度非常大。此阶段,含水率基本维持在某一稳定值,渗透系数趋近于0,衰减速率上的差异性趋于不明显[12],称之为结合水膜段。
以上A′,A,B,C点称为土-水特征曲线的特征点。
3 简化渗透系数预测模型
3.1 渗透系数分段表达式建立原则
由于土-水特征曲线和渗透曲线本质都是描述土体内部孔隙中液相流动存在的可能性,它们之间必定存在某种相似性。对32组不同土样的渗透系数进行统计分析,结果显示:所研究土样的渗透系数曲线对应于各自的土-水特征曲线均可被分成4段,即弯液面排水段,大、中孔隙排水段,微孔隙排水段和结合水膜段,且在每段上服从一定的统计规律,只是对于不同的土样每个阶段所占的比例不同。

表1 海淀东北旺乡及曲周地区土层参数Table 1 Parameters of the soils
通过以上分析,根据各阶段主要影响因子分段建立表达式。因为非饱和土含水率的测定比较容易,原则上尽量用含水率建立渗透系数的预测方程。但对于弯液面排水段含水率变化很小,直接建立K与θ的关系易增大误差,所以首先通过吸力建立函数关系,然后结合VG模型间接确定关于θ的表达式。
3.2 各分段渗透系数变化规律的统计分析
3.2.1 统计模型计算方法
目前,渗透曲线上专有点的渗透系数按下列方法求解,该模型假定土体结构可由半径不同但相互连通的毛细管网络来代表,网络中的液体只能在被液体充满的毛细管中流动。由于被液体填充的孔隙分布与吸力有关,只需预先知道某土样的土-水特征曲线(SWCC)和土样在饱和时的渗透系数,就能够很好地预测出土样在不同饱和度情况下的渗透系数[1,4],即
(i=1,2,…) 。
(3)
(i=1,2,…) 。
(4)
式中:Kw(θw)i为用第i个间段的体积含水率(θw)i确定的渗透系数(m/s)。i为间段编号,随体积含水率的减小而增加。例如,当i=1时,表示第一个间段,即紧靠饱和体积含水率θs。当i=m时,则表示最末一个间段,相应于试验土-水特征曲线上最低的体积含水率θL(一般取土的残余含水率 θr)。j为从i至m的某个数;m为在土-水特征曲线上,从饱和体积含水率θs到最低体积含水率θL的间段点总数;Ks为实测饱和渗透系数(m/s);Ksc为计算饱和渗透系数(m/s);ua为非饱和土体内孔隙气压力(kPa);uw为非饱和土体内孔隙水压力(kPa);Ad为调整常数,该计算值不会影响Kw(θw)i的最终值,具体请参阅文献[13]。
该方法将土-水特征曲线沿体积含水率轴分成m等份,如图3所示,相应于每一个等分中点的基质吸力可用于计算渗透系数。

图3 根据土-水特征曲线预测渗透系数Fig.3 Prediction of hydraulic conductivity according to the soil-water characteristic curve
3.2.2 土-水特征曲线及其特征点确定
表1为海淀东北旺乡和曲周不同地层非黏性土的颗粒组成、土-水特征曲线VG模型拟合参数及饱和渗透系数[14]。
VG模型表达式如下:
(5)
式中:Se为相对饱和度;α为与土的进气值有关,其中α约等于进气值的倒数;n为与土的孔径分布有关;m为与土体特征曲线的整体对称性有关,常与参数n有特定关系,m=1-1/n。
通过式(5)及表1中参数,在Matlab软件中画出土-水特征曲线,并利用图1所示方法求得各曲线上相应的特征点(见表2)。
3.2.3 渗透系数计算与规律统计
结合式(3)至式(5)计算出各土层的渗透系数曲线,并绘制在直角坐标系中(见图4),可看出并无规律可寻。进一步研究发现,在弯液面排水段,lnK-ψ曲线近似呈线性变化(见图5);大、中孔隙排水段,lnK-lnθ曲线也呈现相同规律(见图6);微孔隙排水段在直角坐标系中变化率很小(见图4含水率较低范围段),K-θ曲线近似按线性处理。

表2 各土层水-土特征曲线特征点Table 2 Feature points of SWCC for unsaturated soils

图4 各土层含水率与渗透系数关系Fig.4 Relationship between water content and hydraulic conductivity of each soil stratum
3.3 建立分段简化模型表达式
综合以上分析,在弯液面排水段可设:
lnK=aψ+b或lnK=af(θ)+b,
0<ψ≤或ψa或θa≤θ<θs。
(6)

图5 弯液面排水段各土层基质吸力与渗透系数关系Fig.5 Relationship between matric suction and hydraulic conductivity of each soil stratum in meniscus drainage section
式中:ψa,θa,θs分别为进气值点的吸力、含水率以及

图6 大、中孔隙排水段各土层含水率与渗透系数关系Fig.6 Relationship between water content and hydraulic conductivity of soil strata in drainage segment with large and medium sized voids
饱和含水率。
将(Ks,ψ→0)和(Ka,ψa)代入式(6)得a,b的值,即

(7)
b=lnKs。
(8)
式中:Ka,Ks分别为进气值点的渗透系数及实测的饱和渗透系数。
将式(7),(8)代入式(6)得:

f(θ)lnKs,0<ψ≤ψa或θa≤θ<θs。
(9)
同理,大、中孔隙排水段建立lnK-lnθ的线性函数有:

θb≤θ<θa。
(10)
式中:Kb,θb分别对应图1中B点的渗透系数及含水率。
对于颗粒级配不良的非黏性土,微孔隙排水段所占比例很小,且在该阶段渗透系数衰减速率差异性不明显,其K-θ曲线可按线性处理:
(11)
结合水膜段有:
K=0,θ<θr。
(12)
综合式(9)至式(12)得级配不良的非黏性土的非饱和渗透系数在全范围内的分段表达式为:
(13)
(14)
式中:θa,θb,θr和饱和渗透系数Ks易通过试验测定;因渗透曲线连续,Ka,Kb的值可由式(3),(4)以及式(13)中的第2式间接计算。求解该模型所涉及的试验易于操作,计算过程简单且计算量小,大大降低了间接预测非饱和土渗透系数的难度。实际操作中,A′,C两点容易确定,问题关键在于确定出A,B两特征点,本文给出了作图解法,但尚不够严谨,具体可靠的求法将在后续研究中完成。
4 试验验证与问题讨论
(1) 研究发现:因黏粒含量和颗粒粗细的不同,土体的渗透系数在较低基质吸力下出现不同程度的突降。黏粒含量越高、颗粒越细发生突降时所对应的基质吸力越小(远小于进气值),突降幅度越大;黏粒含量越低,颗粒越粗突降越不明显;砂类土几乎不发生突降,与分段简化模型吻合极好。这导致式(13)中第1式对于砂类土预测准确,而对于有效孔径较小、黏粒含量较高的细粒土预测结果严重偏大。图7为粉质黏土、壤质细砂土和Superstition砂的实测值[15]与预测值对比情况,其中,粉质黏土细粒含量和黏粒含量均很高;壤质细砂土黏粒含量中等,粒径中等;Superstition砂黏粒含量极少,颗粒较粗。图7表明,粉质黏土、壤质细砂土和Superstition砂拟合精度依次增加。

图7 渗透系数实测值与预测值的对比Fig.7 Comparison between measured and predicted results of hydraulic conductivity


图8 渗透系数实测值与预测值的对比Fig.8 Comparison between measured and predicted results of hydraulic conductivity
(3)建立微孔隙排水段的渗透系数预测方程时本文按线性关系简化处理,这只适用于颗粒级配不良的非黏性粗粒土,因为在该类土中微孔隙排水段所占比例很少,在微小区间单元、渗透系数衰减速率差异性不明显的情况下进行线性简化是可行的。但对于颗粒级配良好粒径较小的黏性土等小孔隙多孔介质,微孔隙排水段占了很大比例,此阶段受基质吸力和结合水膜的共同影响,渗透系数在整体上并不是呈线性变化,应同时对这2个方面进行耦合分析,而不能简单地做线性简化。
(4)式(13)和式(14)仅是建立在统计分析的基础上,并没有涉及非饱和土的本构理论,但这种统计规律的存在一定程度上证明了区段划分的正确性。对于非饱和土而言,这种分段研究问题的途径和分段依据的提出可能为其他研究者提供一些新的思路。
5 结 论
本文基于土-水特征曲线,研究了级配不良的非黏性土的非饱和渗透系数变化规律,得出以下结论:
(1)在高含水率(θa>θ>θb)状态下,渗透系数对含水率的变化非常敏感;而在低含水率(θ<θb)状态下,渗透系数随含水率的变化较小,且随着含水率的继续减小其变化率也越来越小。
(2)在低基质吸力(0<ψ≤ψa)时,lnK-ψ曲线呈线性变化;而当θb<θ≤θa时,lnK-lnθ曲线也有类似变化规律。
(3)相应于非饱和土,土-水特征曲线上的不同阶段,影响渗透系数变化的因素各不相同,根据其主要影响因子分段建立表达式是可行的,且分段表达式适用范围相互之间没有约束,表达式可独立应用,非常方便。
[1] 蔡国庆, 赵成刚, 刘 艳. 一种预测不同温度下非饱和土相对渗透系数的间接方法[J]. 岩土力学,2011,32(5): 1405-1410.(CAI Guo-qing,ZHAO Cheng-gang, LIU Yan. Temperature Effects on Soil-water Characteristic Curve of Unsaturated Soils[J]. Rock and Soil Mechanics, 2011, 32(5): 1405-1410. (in Chinese))
[2] JARVIS N J, MESSING I. Near-saturated Hydraulic Conductivity in Soils of Contrasting Texture Measured by Tension Infiltrometers[J]. Soil Science Society of America Journal, 1995, 59(1): 27-34.
[3] AGUS S S, LEONG E C, SCHANZ T. Assessment of Statistical Models for Indirect Determination of Permeability Functions from Soil-water Characteristic Curves[J]. Géotechnique,2003, 53(2): 279-282.
[4] CHILDS E C, COLLIS-GEORGE N. The Permeability of Porous Materials[J]. Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences, 1950, 201(1066): 392-405.
[5] BURDINE N T. Relative Permeability Calculations from Pore Size Distribution Data[J]. Journal of Petroleum Technology, 1953, 5(3): 71-78.
[6] MUALEM Y. Hydraulic Conductivity of Unsaturated Porous Media: Generalized Macroscopic Approach[J]. Water Resources Research, 1978, 14(2): 325-334.
[7] MUALEM Y, KLUTE A. Hydraulic Conductivity of Unsaturated Soils: Prediction and Formulas[J]. Methods of Soil Analysis. Part 1. Physical and Mineralogical Methods, 1986: 799-823.
[8] VAN GENUCHTEN M T. A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils[J]. Soil Science Society of America Journal,1980, 44(5): 892-898.
[9] BURDINE N T. Relative Permeability Calculation from Size Distribution Data[J]. Transactions, American Institute of Mining, Metallurgical, and Petroleum Engineers, 1953, 198:71-78.
[10]MUALEM Y. Hydraulic Conductivity of Unsaturated Porous Media: Generalized Macroscopic Approach[J]. Water Resources Research , 1978, 14(2):325-334.
[11]FREDLUND D G, XING A, HUANG S. Predicting the Permeability Function for Unsaturated Soils Using the Soil-water Characteristic Curve[J]. Canadian Geotechnical Journal, 1994, 31(4): 533-546.
[12]叶为民, 钱丽鑫, 白 云, 等. 由土-水特征曲线预测上海非饱和软土渗透系数[J]. 岩土工程学报, 2005, 27(11): 1262-1265.(YE Wei-min, QIAN Li-xin, BAI Yun,etal, Predicting Coefficient of Permeability from Soil-water Characteristic Curve for Shanghai Soft Soil[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(11): 1262-1265. (in Chinese))
[13]FREDLUND D G,RAHARDJO H. Soil Mechanics for Unsaturated Soils[M]. New York: John Wiley & Sons, 1993:256-278.
[14]王 康. 非饱和土壤水流运动及溶质迁移[M]. 北京: 科学出版社, 2010:32-35.(WANG Kang. Water Movement and Solute Migration of Unsaturated Soil[M]. Beijing:Science Press,2010:32-35.(in Chinese))
[15]RICHARDS L A. Water Conducting and Retaining Properties of Soils in Relation to Irrigation[C]// Proceeding of an International Symposium on Desert Research, Jerusalem, May 7-14, 1952: 523-546.
[16]孙大松, 刘 鹏, 夏小和, 等. 非饱和土的渗透系数[J]. 水利学报,2004, 3(8): 71-75. (SUN Da-song, LIU Peng, XIA Xiao-he,etal. Permeability Coefficient of Unsaturated Soils [J]. Journal of Hydraulic Engineering,2004, 3(8):71-75. (in Chinese))
(编辑:黄 玲)
Segmented Simplified Model for Hydraulic Conductivity Curve of Unsaturated Soil
WANG Xiao-feng1,2,SHI Hong-lian1,WANG Zhen1,WU Liu-dong1
(1. Faculty of Engineering, China University of Geosciences, Wuhan 430074, China;2. Shandong Zhengyuan Construction Engineering Co., Ltd., Yantai 264670, China)
The soil-water characteristic curve is divided into four segments based on the main factors affecting the hydraulic conductivity coefficient of unsaturated soil. On this basis, a segmentation simplified model for hydraulic conductivity of unsaturated cohesionless soil with bad gradation was created. A complete predictive curve can be obtained just with a small amount of measured or calculated hydraulic conductivities of different moisture conditions. Curve of lnK-lnΨat low matric suction(0<ψ<ψa)and curve of lnK-lnθwhenθb<θ<θaare verified to be linear.
unsaturated soil; hydraulic conductivity; segmented simplified model;soil-water characteristic curve;matric suction
10.3969/j.issn.1001-5485.2015.02.016
2013-08-30;
2013-09-17
国家自然科学基金项目(41272307);教育部长江三峡库区地质灾害研究中心开放基金(TGRC201011)
王晓峰(1988-),男,山东滨州人,助理工程师,硕士,主要从事土-水相互作用机理研究和岩土工程设计工作,(电话)13655352233(电子信箱)964547554@qq.com。
时红莲(1969-),女,河南郑州人,副教授,硕士,主要从事岩土工程性质的试验及基础工程设计工作,(电话)13871279685(电子信箱)shhl2000@126.com。
TU411.91
A
1001-5485(2015)02-0072-06
2015,32(02):72-77,83
