利用体积分方程的弱化BCGS算法模拟倾斜及层状各向异性地层中井间电磁响应

常欣莉, 党峰, 魏宝君, 陈涛, 王成园

(1.中国石油大学(华东)理学院, 山东 青岛 266580; 2.中国石油集团测井有限公司, 陕西 西安 710077)

0 引 言

井间电磁成像技术是将发射器置于发射井中,在一口或多口邻近的井中接收电磁信号并通过对数据进行反演成像从而获得井间油气藏分布的方法[1-3]。数值模拟算法研究是研发井间电磁成像仪器、分析井间电磁探测特性和对井间电磁测量数据进行成像的前提。三维电磁场数值模拟算法的研究在20世纪70年代中期就已开始,积分方程算法[4-6]、有限元素法[7]和有限差分法[8-10]都得到了广泛应用。与需离散求解整个井间区域的有限元法和有限差分法相比,体积分方程法只需对三维异常体区域进行离散,具有快速、方便等特点,是计算三维井间电磁响应的一种有效方法。Hohmann和Wannamaker等用体积分方程法计算了简单的三维模型,鲍光淑等[11]采用积分方程法计算出空间任一点的电场和磁场,魏宝君等[12-13]提出了改进型局域非线性迭代算法求解积分方程,徐凯军等[14]利用积分方程法实现了均匀导电半空间三维大地电磁响应的数值模拟。

传统的关于体积分方程的应用一般只限于各向同性地层[15-17],而陈桂波等[18]则将体积分方程用于各向异性地层,模拟了层状各向异性地层中三维异常体的散射电磁波,并将层状各向异性地层作为背景层,但该文献没有考虑倾斜井的情况。本文将体积分方程与层状各向异性介质中并矢Green函数的递推矩阵方法[19-20]相结合模拟倾斜井及层状各向异性地层中的井间电磁的响应。体积分方程的求解通过弱化BCGS算法这一完全解法实现,计算时将层状各向异性原状地层作为背景地层,从而将计算区域限制在三维异常体区域内,使未知量数目和计算量均大大减少,计算精度和效率同时得到保证。

1 基本理论

1.1 层状各向异性地层中的体积分方程

所采用的井间地层模型见图1。该模型包含了水平层状各向异性原状地层和电导率异常区域。每层背景地层的电导率张量均可表示为σb=diag(σhb,σhb,σvb),其中σhb为背景地层的水平电导率,σvb为背景地层的垂直电导率,不同层的电导率张量不同。将发射线圈视为磁偶极子并假设发射源随时间的变化关系为exp(iωt),其中ω为角频率,则接收井中接收线圈处的磁场强度矢量可表示为体积分方程形式

Δσ(r′)·E(r′,rT)dr′

(1)

式中,rT、rR分别为发射线圈和接收线圈的位置坐标;D为包含电导率异常体的积分区域;GHJ(rR,r′)为层状各向异性背景地层中r′处的单位电流元在接收点rR处的磁型并矢Green函数;Δσ(r′)=σ(r′)-σb(r′)=diag(Δσh,Δσh,Δσv)为异常体与背景地层电导率张量之差;E(r′,rT)为发射线圈在积分区域内产生的总电场;Hb(rR,rT)为发射源在层状各向异性背景地层中产生的磁场强度。式(1)称为数据方程,若积分区域内的总电场E(r′,rT)已知,由式(1)可获得接收线圈处的磁场强度。将水平层状各向异性原状地层作为背景地层,积分区域D就是电导率异常区域,从而使未知量数目和计算量均大大减少。

图1 地层模型

在积分区域D内,总电场强度矢量E(r,rT)满足

Δσ(r′)·E(r′,rT)dr′,r∈D

(2)

式中,GEJ(r,r′)为层状各向异性背景地层中r′处的单位电流元在场点r处的电型并矢Green函数;Eb(r,rT)为发射源在层状各向异性背景地层中产生的电场强度。式(2)称为目标方程,该式是计算异常体内总电场分布的第二类Fredholm积分方程。

GEJ在r=r′处存在强奇异性,在积分区域D内不能直接求解式(2),而是根据GEJ与GAJ所满足的关系

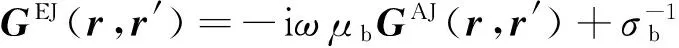
E(r,rT)=Eb(r,rT)+

Δσ(r′)·E(r′,rT)dr′r∈D

(3)

式中,μb为背景地层的磁导率,由于假设地层是非磁性的,故取μb为真空中的值μ0;GAJ(r,r′)为层状各向异性背景地层中r′处的单位电流元在场点r处的磁矢势并矢Green函数。由于GAJ的奇异性大大降低并且对其含奇异点的积分可以进行弱化处理,故求解式(3)可避免奇异值的出现。

将积分区域D分成N个立方体形小单元Dj(j=1,2,…,N),其体积为ΔVj。假设每个小单元内异常体与背景地层的电导率张量之差恒定,设为Δσj,并假设在每个小单元内电场强度值恒定,由其中心点的值代替,则式(1)的离散形式为

Δσj·E(rj,rT)ΔVj

(4)

式(3)的离散形式为

E(ri,rT)=Eb(ri,rT)+

Δσj·E(rj,rT)ri∈D,i=1,2,…,N

(5)

式(5)可表示为线性形式

(6)

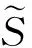
(7)

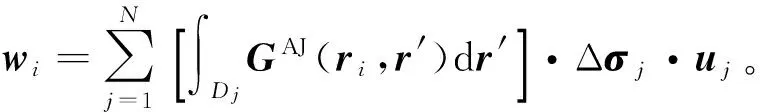
式(6)可采用稳定型双共轭梯度(BCGS)方法进行迭代求解[21],从而得到总电场强度在异常区域D内的分布。将采用上述算法得到的总电场强度E(ri,rT)代入式(4),即可得到接收线圈处的磁场强度在地层直角坐标系中的各个分量。

根据发射线圈和接收线圈方向的不同,磁场强度各分量可表示为矩阵形式

(8)

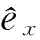
H∥(rR,rT)=Hxxcosα1cosα2+Hyxcosα1cosβ2+Hzxcosα1cosγ2+Hxycosβ1cosα2+Hyycosβ1cosβ2+Hzycosβ1cosγ2+Hxzcosγ1cosα2+Hyzcosγ1cosβ2+Hzzcosγ1cosγ2

(9)

1.2 层状各向异性背景地层的并矢Green函数

设发射线圈的磁偶极矩为MT,则式(1)和式(3)中发射源在背景地层中产生的电场强度和磁场强度可表示为

Eb(r,rT)=GEM(r,rT)·MT

(10)

Hb(rR,rT)=GHM(rR,rT)·MT

(11)

式中,GEM和GHM分别为水平层状各向异性背景地层中单位磁偶极子源产生的电型和磁型并矢Green函数。魏宝君等[20]给出了计算层状各向异性介质中磁偶极子源和电偶极子源并矢Green函数的递推矩阵方法,可快速精确地求解式(1)和式(3)所需要的GEM、GHM和GHJ。

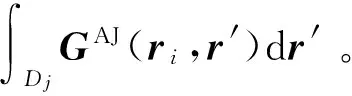
(12)

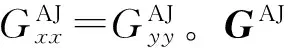
若源点r′和场点ri不在同一地层中,则GAJ只包含散射项SGAJ。若源点r′和场点ri在同一地层中,GAJ除包含散射项外还包含背景项PGAJ。若r′和ri虽在同一地层中但i≠j,即ri不在小单元Dj内,则对PGAJ的积分不存在奇异值问题,可近似为

若i=j,则对PGAJ的积分存在奇异值问题,需进行弱化处理。PGAJ各分量的具体表达式为

(13)

(14)

(15)

(16)

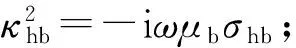
(17)

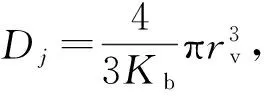
(18)

对于式(14)和式(15)的积分,由于被积函数在小单元Dj内是相对于中心点rj的奇函数,故有

(19)

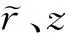
2 数值算例及讨论

采用体积分方程的弱化BCGS算法对层状各向异性背景地层中的多分量井间电磁响应进行数值模拟,并分析发射井和接收井的倾角、背景地层的各向异性等因素对井间电磁响应的影响。所采用的模型为3层各向异性地层模型(见图1),上、下层电导率分别为σhb1=0.1 S·m-1、σvb1=0.1 S·m-1,σh3=0.1 S·m-1、σvb3=0.1 S·m-1。中间层σhb2=1.0 S·m-1、σvb2大小可变,厚度为10.0 m。上、下层界面垂向坐标分别为z1=10 m、z2=20 m。在中间地层中有一个10 m×10 m×10 m的各向同性电导率异常体,其电导率为σa=0.02 S·m-1。电导率异常体在x、y、z方向划分的单元数目均为5,小单元总数为125,每个小单元的尺寸为2 m×2 m×2 m。发射源置于发射井中垂向坐标为15 m处,电导率异常体在井间居中。取发射源磁偶极矩为MT=1 A·m2,频率1 kHz。取发射源与第1个接收点的井间横向距离为100 m,若接收井倾斜,井间距则随接收点垂向位置的增加而增加。

2.1 倾角对井间电磁响应的影响

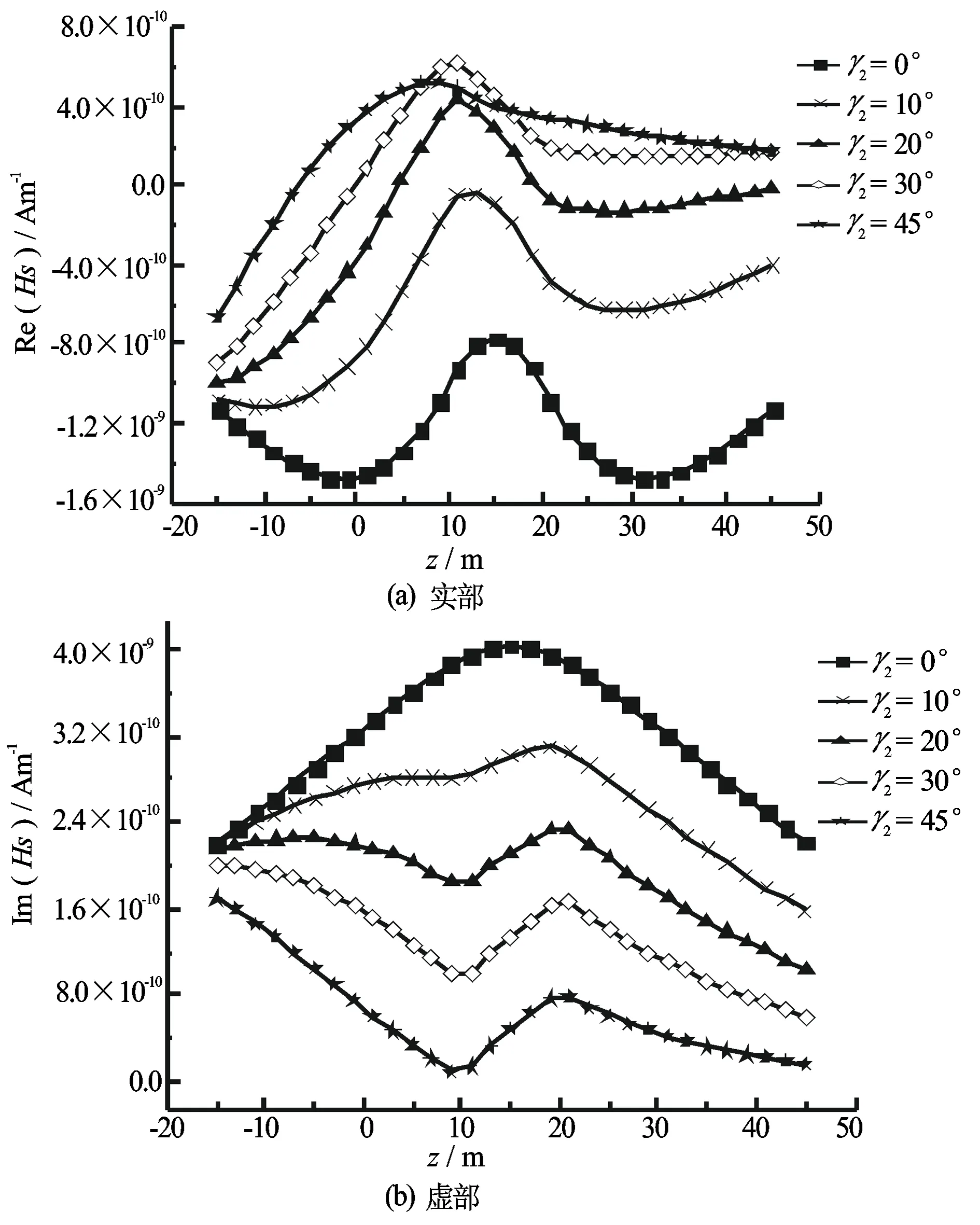
图2 接收井倾斜时散射磁场轴向分量随接收点垂向位置的变化

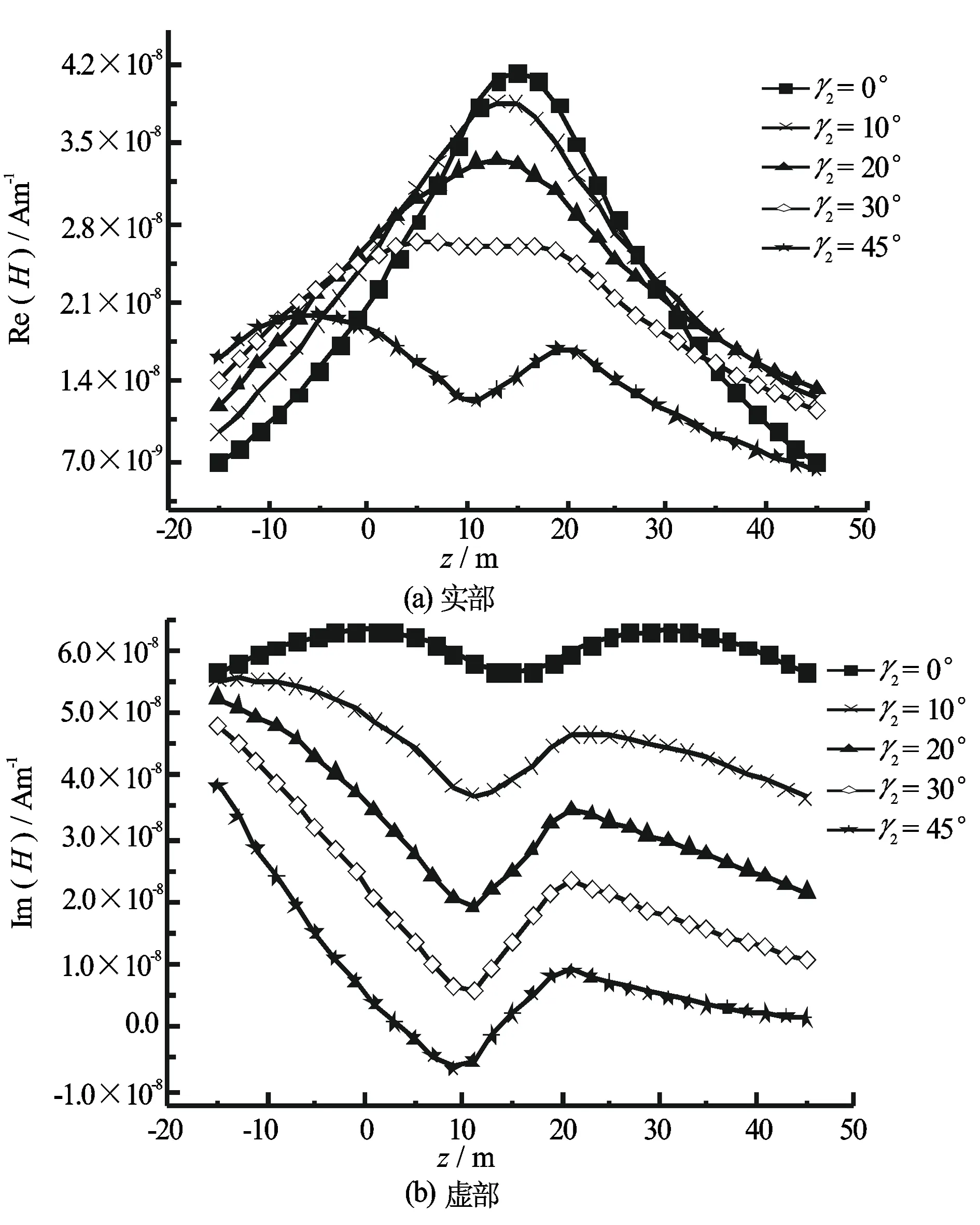
图3 接收井倾斜时总磁场轴向分量随接收点垂向位置的变化

假设背景层各向同性,即σvb2=1.0 S·m-1。取发射井和接收井在同一个xoz面上,即β1=β2=90 °。以发射井垂直、接收井倾斜为例,此时井间距随接收点垂向位置的增加而增加。图2和图3分别给出了接收井倾斜角度不同时散射磁场和总磁场轴向分量随接收点垂向坐标的变化。可以看出,倾斜井中磁场的轴向分量与倾斜角度及井间距密切相关,倾斜角度及井间距的变化既改变了磁场峰值的位置也改变了峰值的大小。且倾角越大其虚分量指示地层界面的位置就越准确。若接收井和发射井均倾斜,磁场响应情况类似,此时磁场轴向分量变为4个分量的投影组合。

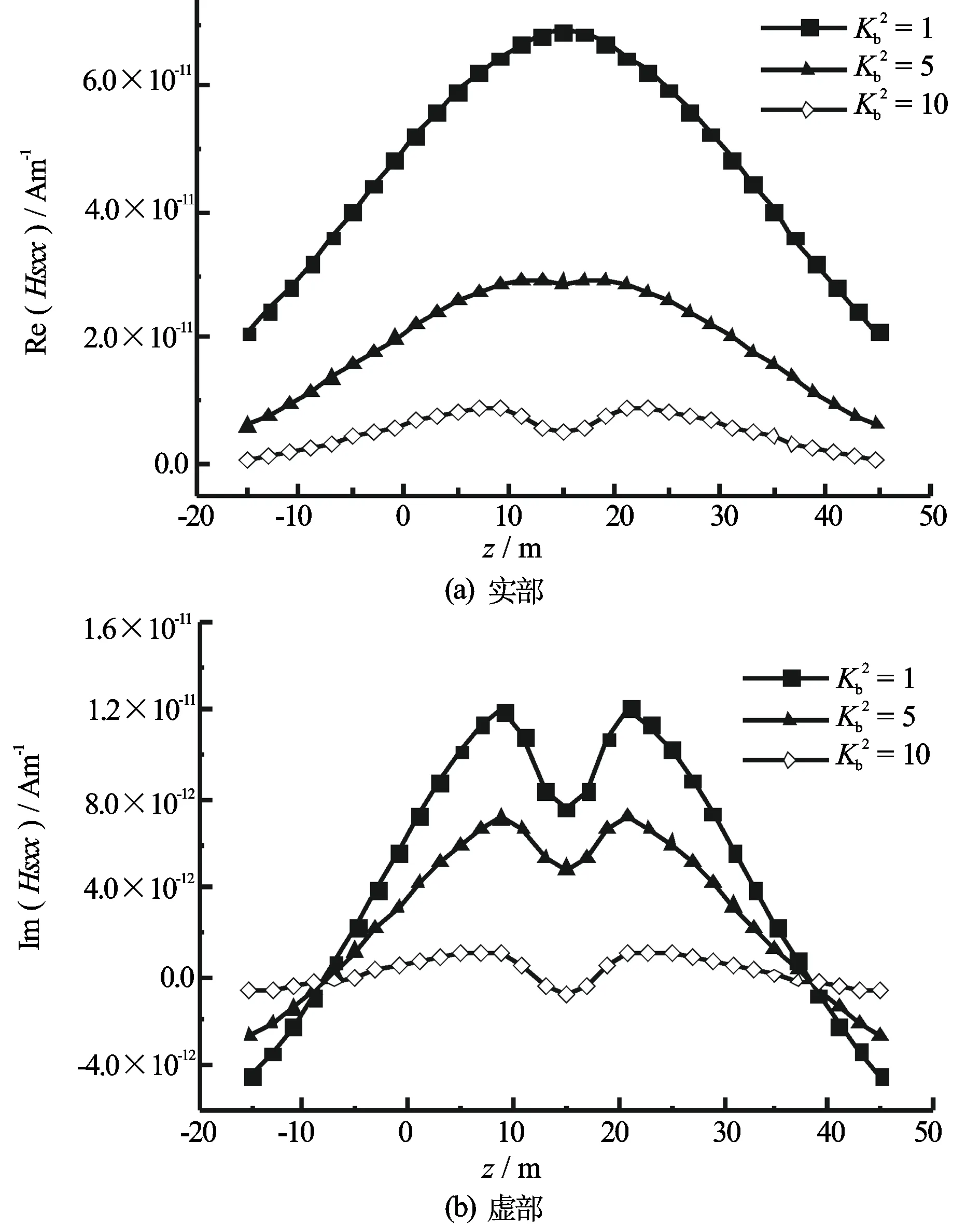
图4 散射磁场xx分量随接收点垂向位置的变化

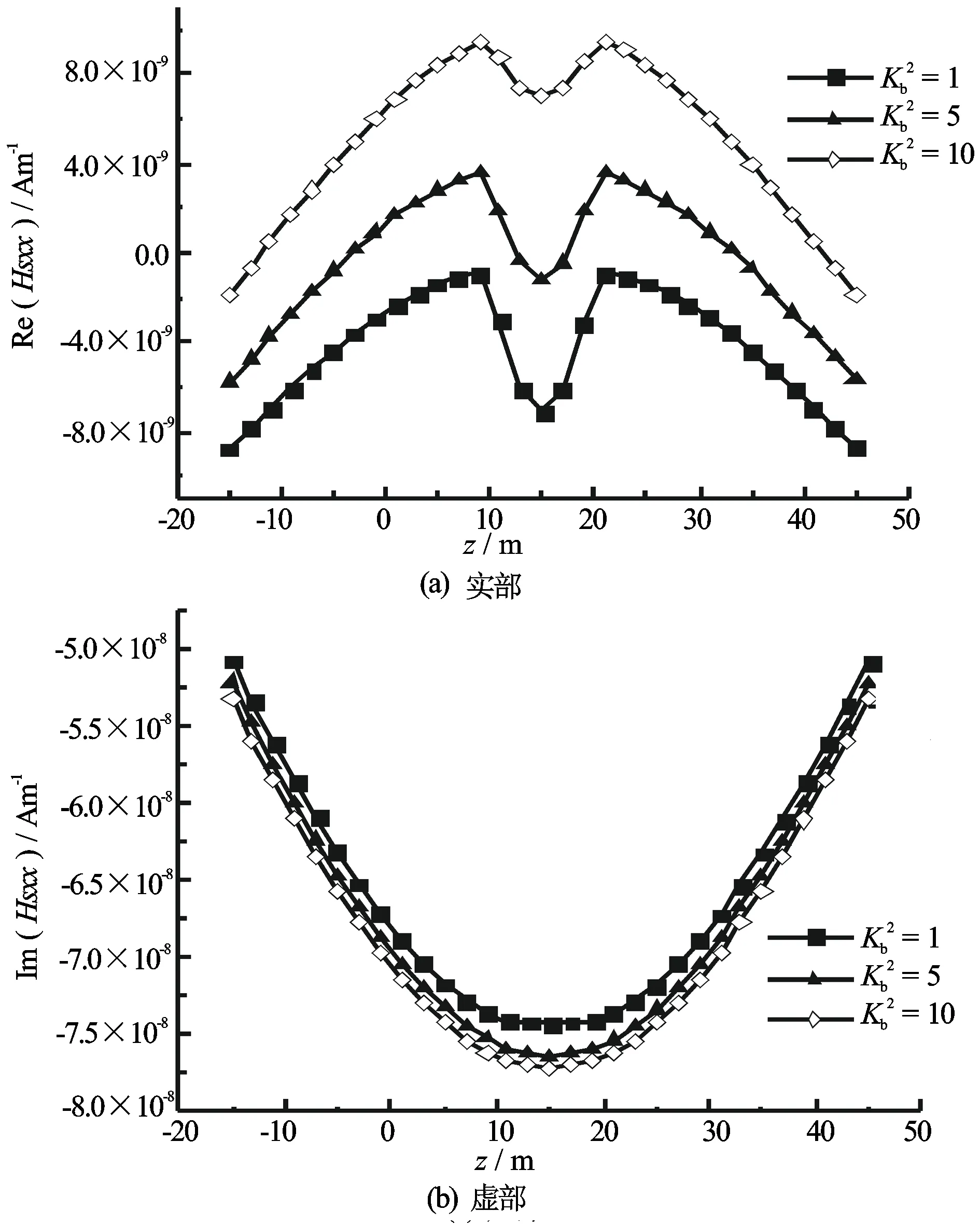
图5 总磁场xx分量随接收点垂向位置的变化

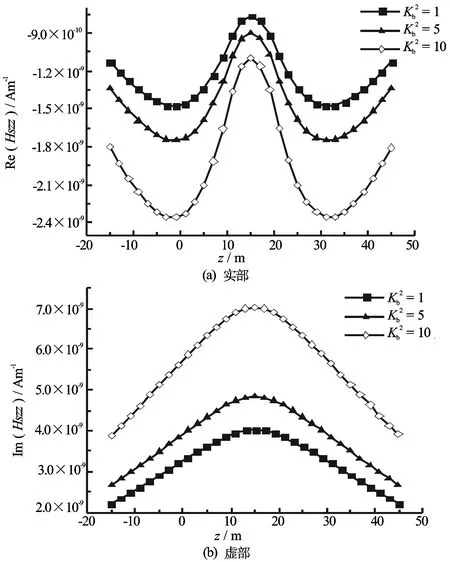
图6 散射磁场zz分量随接收点垂向位置的变化

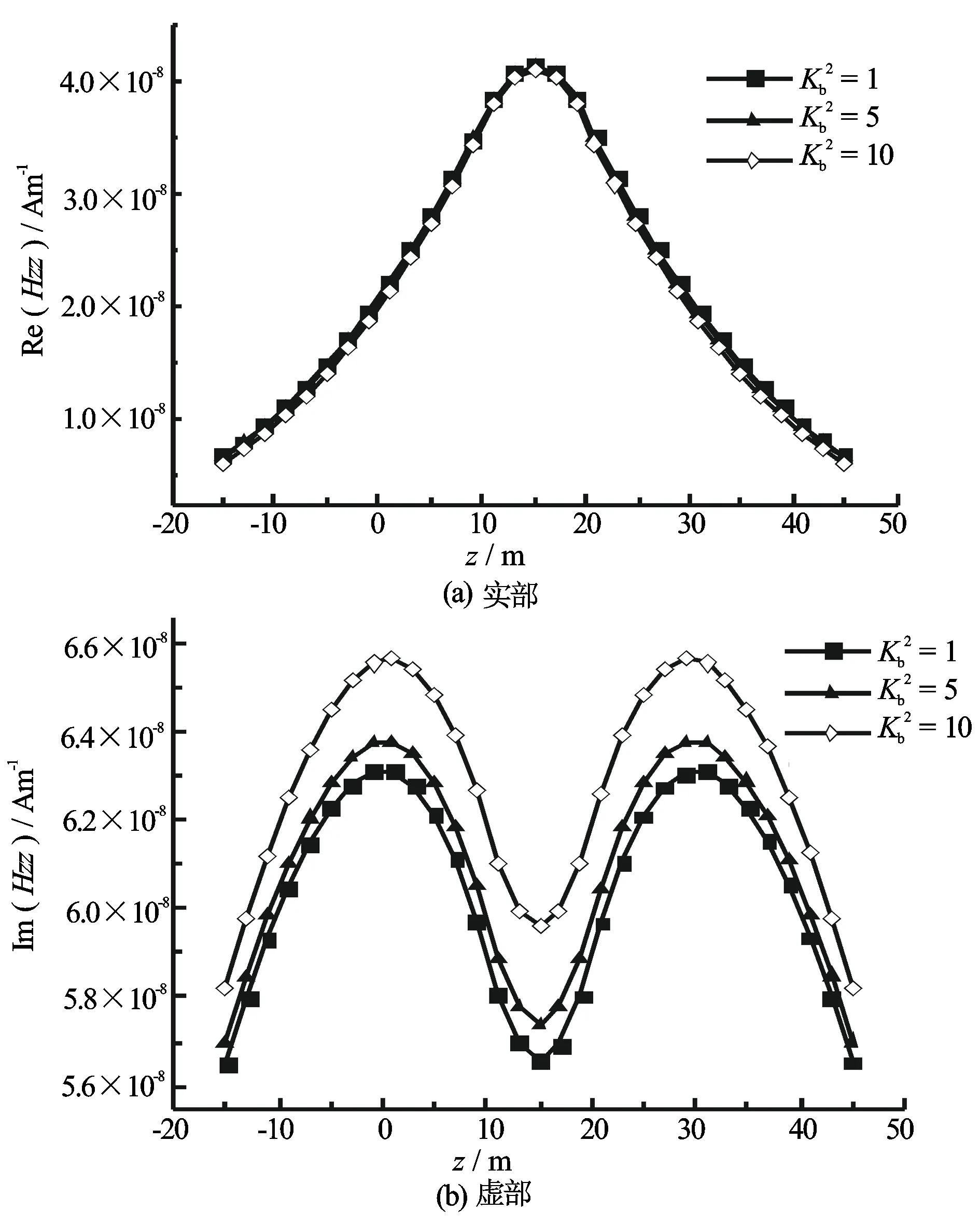
图7 总磁场zz分量随接收点垂向位置的变化

2.2 背景层各向异性对井间电磁响应的影响

图8 接收井倾斜30 °时散射磁场轴向分量随接收点垂向位置的变化

通过改变σvb2的大小改变背景层电导率各向异性系数,并模拟背景层电导率各向异性程度不同时的井间电磁响应,假设发射井和接收井均垂直于地层界面。图4和图5分别给出了背景层各向异性系数不同时散射磁场和总磁场的xx分量随接收点垂向坐标的变化。由图4和图5可以看出,xx分量散射磁场的强度与总磁场的强度相比要小得多,利用该分量不易于探测出电导率异常体的存在。另外,不同的各向异性系数对总磁场Hxx的实分量影响较大,且在实分量中出现的“犄角”可以明显地指示地层界面的位置,而各向异性系数对Hxx虚分量的影响则相对较小。图6和图7分别给出了背景层各向异性系数不同时散射磁场和总磁场的zz分量随接收点垂向坐标的变化。由图6和图7可以看出,zz分量散射磁场的强度数值较大,利用该分量可探测电导率异常体的存在,并且该项受背景层各向异性系数的影响较大。当然,在该模型中由于电导率异常体体积有限,磁场散射项强度仍小于背景项强度,所以总磁场受各向异性影响程度相对较小。

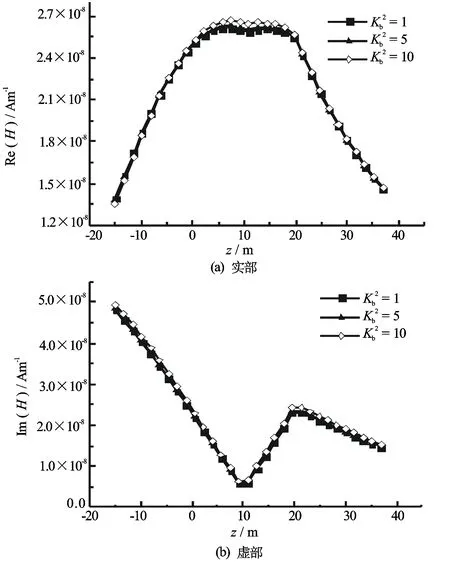
图9 接收井倾斜30 °时总磁场轴向分量随接收点垂向位置的变化

2.3 背景层各向异性和倾角对井间电磁响应的影响

模拟背景层电导率各向异性和井斜同时存在时的井间电磁响应,仍假设发射井和接收井同在xoz平面上。首先考虑发射井垂直、接收井倾斜30 °时散射磁场和总磁场轴向分量随接收点垂向坐标的变化,计算结果见图8和图9。由于磁场背景项不受地层各向异性的影响,散射项虽受各项异性的影响但其强度与总磁场相比相对较弱,所以总磁场轴向分量受电导率各向异性影响仍然较小。然后考虑发射井和接收井均倾斜30 °的情况,即γ1=γ2=30 °,其总磁场轴向分量随接收点垂向坐标的变化如图10所示。当发射井和接收井同时倾斜时,其轴向分量由Hxx、Hzx、Hxz、和Hzz这4个分量投影而成。总磁场Hxx的实分量受地层电导率各向异性影响较大,在此情况下总磁场轴向分量受地层各向异性的影响较为明显。

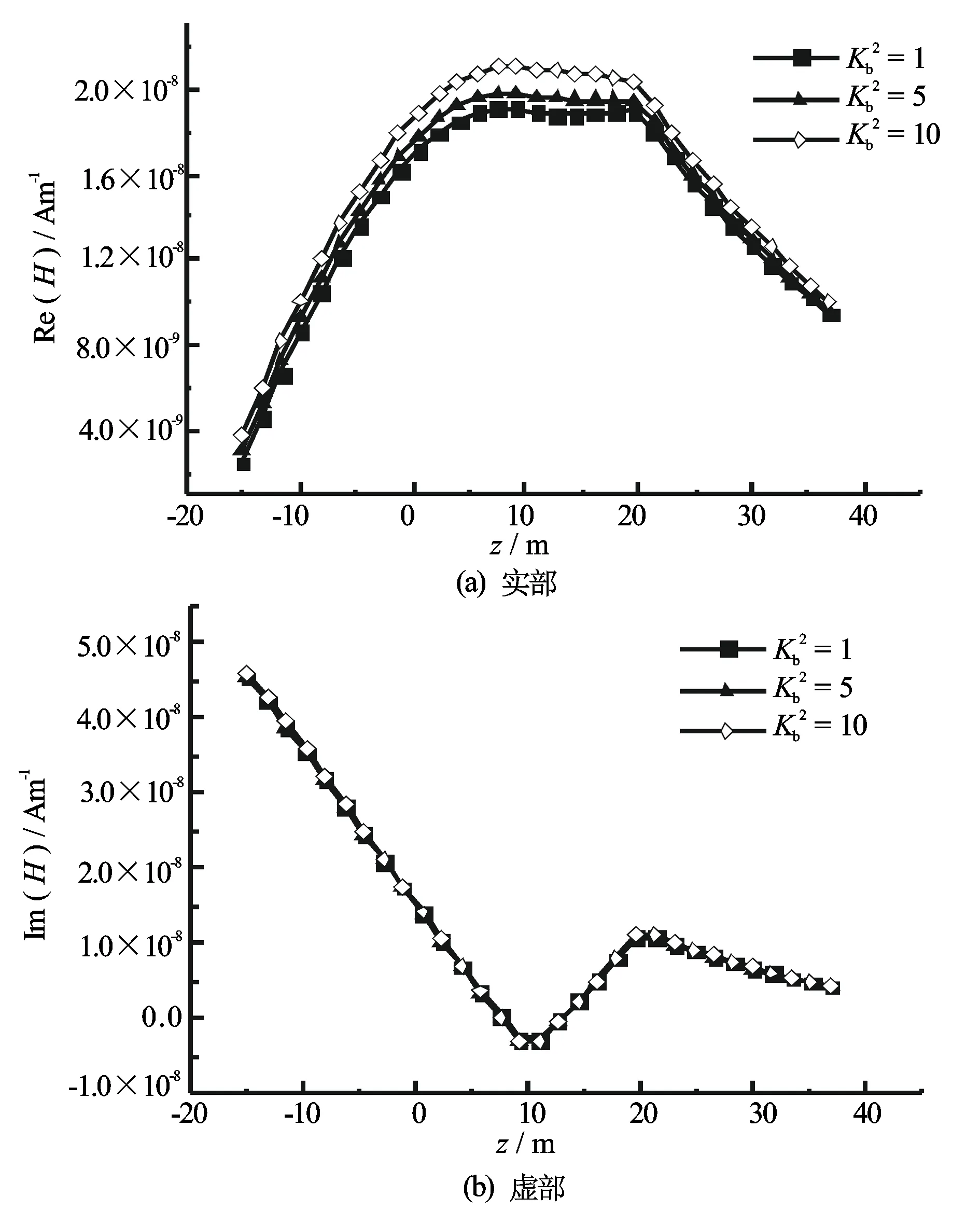
图10 发射井和接收井均倾斜30 °时总磁场轴向分量随接收点垂向位置的变化

3 结 论

(1) 将层状各向异性介质并矢Green函数的递推矩阵方法与体积分方程的弱化BCGS算法有机结合,由于将计算区域限制在电导率异常体区域内,使未知量数目和计算量均大大减少,可有效模拟倾斜井及层状各向异性地层中的井间电磁响应。

(2) 利用上述算法的数值模拟结果表明,当接收井发生倾斜时,倾角越大磁场轴向分量的虚分量越能准确指示地层界面的位置;xx分量散射磁场的强度与总磁场的强度相比要小得多,利用该分量不易于探测出电导率异常体的存在;不同的各向异性系数对总磁场Hxx影响较大,且在其实分量中出现的“犄角”可以明显指示地层界面的位置;zz分量散射磁场的强度数值相对较大,利用该分量可探测电导率异常体的存在,并且该项受背景层各向异性系数的影响亦较大。

参考文献:

[1] Wilt M, Morrison H, Becker A, et al. Crosshole Electromagnetic Tomography: A New Technology for Oil Field Characterization [J]. The Leading Edge, 1995, 14(3): 173-177.

[2] Hoversten G, Newman G, Morrison H, et al. Reservoir Characterization Using Crosswell Electromagnetic Inversion: A Feasibility Study for the Snorre Field, North Sea [J]. Geophysics, 2001, 66(4): 1177-1189.

[3] 曾文冲, 赵文杰, 臧德福. 井间电磁成像系统应用研究 [J]. 地球物理学报, 2001, 44(3): 411-420.

[4] Hohmann G W. Three-dimensional Induced Polarization and Electromagnetic Modeling [J]. Geophysics, 1975, 40(2): 309-324.

[5] Wannamaker P E, Hohmann G W, SanFilipo W. Electromagnetic Modeling of Three-dimensional Bodies in Layered Earths Using Integral Equations [J]. Geophysics, 1984, 49(1): 60-74.

[6] Newman G A, Hohmann G W, Anderson W L. Transient Electromagnetic Response of a Three-dimensional Body in a Layered Earth [J]. Geophysics, 1986, 51(8): 1608-1627.

[7] Pridmore D F, Hohmann G W, Ward S H, et al. An Investigation of Finite-element Modeling for Electrical and Electromagnetic Data in Three Dimensions [J]. Geophysics, 1981, 46(7): 1009-1024.

[8] Alumbaugh D L, Newman G A, Prevost L, et al. Three-dimensional Wideband Electromagnetic Modeling on Massively Parallel Computers [J]. Radio Science, 1996, 31(1): 1-23.

[9] 沈金松. 用交错网格有限差分法计算三维频率域电磁响应 [J]. 地球物理学报, 2003, 46(2): 281-288.

[10] 沈金松. 用有限差分法计算各向异性介质中多分量感应测井的响应 [J]. 地球物理学进展, 2004, 19(1): 101-107.

[11] 鲍光淑, 张碧星, 敬荣中. 三维电磁响应积分方程法数值模拟 [J]. 中南工业大学学报, 1999, 30(5): 472-474.

[12] 魏宝君, 张庚骥, 胡波. 用改进的局域非线性迭代方法计算三维井间电磁场 [J]. 石油大学学报, 2002, 26(3): 124-127.

[13] 魏宝君, 张庚骥. 三维井间电磁场的正反演计算 [J]. 地球物理学报, 2002, 45(5): 735-743.

[14] 徐凯军, 李桐林, 张辉, 等. 利用积分方程法的大地电磁三维正演 [J]. 西北地震学报, 2006, 28(2): 104-107.

[15] Wei B J, Simsek E, Liu Q H. Improved Diagonal Tensor Approximation (DTA) and Hybrid DTA/BCGS-FFT Method for Accurate Simulation of 3D Inhomogeneous Objects in Layered Media [J]. Waves in Random and Complex Media, 2007, 17(1): 55-66.

[16] Wei B J, Simsek E, Yu C, et al. Three-dimensional Electromagnetic Nonlinear Inversion in Layered Media by a Hybrid Diagonal Tensor Approximation: Stabilized Biconjugate Gradient Fast Fourier Transform Method [J]. Waves in Random and Complex Media, 2007, 17(2): 129-147.

[17] 魏宝君, LIU Q H. 水平层状介质中基于DTA的三维电磁波逆散射快速模拟算法 [J]. 地球物理学报, 2007, 50(5): 1595-1605.

[18] 陈桂波, 汪宏年, 姚敬金, 等. 用积分方程法模拟各向异性地层中三维电性异常体的电磁响应 [J]. 地球物理学报, 2009, 52(8): 2174-2181.

[19] Wei B J, Zhang G J, Liu Q H. Recursive Algorithm and Accurate Computation of Dyadic Green's Functions for Stratified Uniaxial Anisotropic Media [J]. Science in China: Series F, 2008, 51(1): 63-80.

[20] 魏宝君, 王甜甜, 王颖. 用磁流源并矢Green函数的递推矩阵方法计算层状各向异性地层中多分量感应测井响应 [J]. 地球物理学报, 2009, 52(11): 2920-2928.

[21] 魏宝君, LIU Q H. 层状介质中计算体积分方程的弱化BCGS-FFT算法 [J]. 中国石油大学学报: 自然科学版, 2007, 31(1): 49-55.