基于岩电参数和颗粒直径的渗透率模型在低孔隙度低渗透率储层中的应用

魏帅帅, 沈金松,2,3, 汪轩, 李曼

(1.中国石油大学(北京)地球物理系, 北京 102249; 2.油气资源与探测国家重点实验室, 北京 102249; 3.中国石油天然气集团公司物探重点实验室, 北京 102249)

0 引 言

渗透率是储层评价和产能预测的关键物性参数,它控制了储层的油气聚集生成和开采效率。到目前为止,还没有一种原位测试方法可以直接得到渗透率,大多数渗透率数据是由岩心实验测得的压力和流速数据估算得到的[1-2]。许多情况下,岩心取得和实验分析成本很高,加之受到取心和实验测量的不确定性影响,岩心分析的渗透率通常只是限于少量的重点层段。测井数据在井深度上连续均匀,且能反应储层岩石的多类物理性质,研究一种能由测井数据的变换预测渗透率的方法具有重要意义[3-4]。

油气工业界常用测井数据估算渗透率,例如孔隙度—渗透率的统计关系[5-6],这类方法的正确性随地层的孔隙结构和孔隙度分布而变化。估计渗透率的常用经验关系大致可以分为3类参数的组合,即利用孔隙介质的颗粒尺寸,考虑孔隙度大小和结合颗粒比表面与孔隙度。例如Kozeny-Carman模型的修正形式[5,7]考虑了孔隙的比表面和孔隙度大小,Berg模型[1]和Van Baarn模型[8]考虑了颗粒直径和孔隙度大小。这些关系中孔隙度参数很容易由测井数据得到,颗粒直径大小和比表面积值至今仍无法由测井数据直接得到。

研究基于孔隙介质中流体流动与电流之间的动电关系导出的渗透率预测模型,分析了岩石中电流导通性能、孔隙结构连通性对渗透率的影响。利用前人发表的实验数据和岩心测量数据,考察了RGPZ渗透率计算模型对不同岩性和不同孔隙度储层的适应能力。实验数据和实际岩心分析数据的测试对比表明,RGPZ渗透率计算模型对渗透率的预测性能均优于目前常用的渗透率计算关系。文中分析的RGPZ渗透率计算模型是由Glover等[9]基于Andre Revil、Paul Glover、Philippe Pezard和Zamora M通过实验数据的模拟分析在一份内部报告中提出的关系建立的[9]。研究首先回顾了目前常用的渗透率计算关系的关键参数和应用条件;其次,用前人发表的实验数据测试了RGPZ模型预测渗透率的可靠性和精度,并与其他常用渗透率关系的预测结果进行了对比;接着,用低孔隙度低渗透率储层中的压汞分析数据(MICP)和RGPZ渗透率计算模型预测的储层渗透率与实验测试结果进行了对比;最后,用鄂尔多斯实际测井数据检验了RGPZ渗透率计算模型实用性。

1 基于岩电参数的RGPZ渗透率模型的导出

由前人对经典渗透率估算模型的分析[10-14]知道,这些模型均是经验关系或在导出过程中作了简化假设。事实上,由岩石的基本导电关系也可以导出渗透率与岩石孔隙度和岩电参数的关系。由Bussian[15]关于泥质砂岩导电性的分析,岩石的宏观电导率可以表示为

(1)

式中,σf为地层水电导率;σs为岩石骨架的电导率,考虑了岩石颗粒的表面导电性;m为地层胶结指数,反映孔隙结构的弯曲程度,是孔隙结构连通性和复杂性的度量,它是与带电离子迁移过程中电流导通部分的有效孔隙相关的几何参数。

若连通孔隙是由开裂缝组成,那么,地层因素F=1/φ,即m=1,表示所有孔隙都有效地对总电导率有贡献。含黏土岩石情况变得复杂,会呈现较大的胶结指数(m>2.5),表明大部分微孔隙由孤立封闭或/和高弯曲度的电流路径构成,它们无法有效地对导电性做出贡献。若考虑黏土表面的导电性,且定义无量纲参数ξ为表面电导率σs与自由电导率σf之比值,它与导电颗粒比表面积Σs和等效颗粒半径R相关[16]

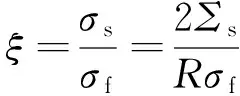
(2)

则ξ可以描述电导率随矿化度变化的规律,对低矿化度ξ>>1,而对高矿化度0<ξ<1,且在高矿化度情况下,式(1)可以用二项式展开简化[15]

(3)

在高矿化度极限条件下,电导率也可由Johnson和Sen[17]给出

(4)

式中,Λ为与连通孔隙体积中电流导通性相关的孔喉特征尺度,可以解释为孔隙介质电流可以通过的等效孔隙半径。然而,它近似等于在连通孔隙体积中控制电流导通的窄喉道的半径[18]。

比较式(3)和式(4)的系数,且当F远大于1时,孔喉特征尺度Λ可以表示为

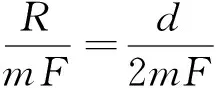
(5)

式中,d=2R为颗粒的平均直径,对于大多数孔隙性介质,F远大于1的条件是成立的。式(5)建立了孔喉特征尺度Λ与地层因素F之间的关系。对稀疏球颗粒处于导电流体中的情况(φ→1),F≈φ-3/2=1+(3/2)(1-φ),与Sen等[19]导出的标准球m=3/2一致。在这一极限条件下,Λ=4R/[9(1-φ)],这一关系早就由Kostek等[2]用不同方法得到。前人业已证明,孔喉特征尺度Λ与流体渗透率有关系[20]:K≈Λ2/(aF),a是与孔隙空间形状相关的常数,处于2～12范围,将前文的Λ代入K的关系得到RGPZ方程

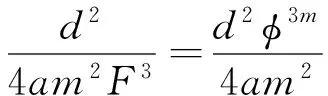
(6)

式中,KRGPZ单位为×10-3μm2;d为相关岩石的颗粒直径大小;φ为分数孔隙度;m为胶结指数;a为颗粒堆积方式相关的参数。对三维体积排列的球形颗粒a=8/3,m=3/2,则式(6)的KRGPZ方程为[21]

KRGPZ=4.16×10-2d2φ4.5

(7)

对大多数纯砂岩颗粒,取a=8/3,m=1.8,KRGPZ方程为[21]

KRGPZ=2.89×10-2d2φ5.4

(8)

注意到式(6)不仅考虑岩石孔隙度和岩石颗粒,还考虑了不同岩性和岩石孔隙结构的变化,因此,可以期望RGPZ模型通过颗粒直径和胶结指数的加入能更好地适应低孔隙度低渗透率致密类岩层和低孔隙度高渗透率缝洞型储层的渗透率预测。图1给出了式(6)的RGPZ模型预测的渗透率随模型中d、m、a和φ变化的关系曲线。图1(a)至图1(c)是在单种岩性中常看到的上凸形曲线。需要注意的是,模型对d、φ和m的变化高度敏感,而对颗粒堆积参数a不灵敏。

图1 RGPZ模型随其主要参数的函数变化

2 RGPZ渗透率估算模型的适应性分析

2.1 玻璃珠堆积模型实验数据的验证

为了考察RGPZ模型对疏松岩石的适应性,用饱和流体的玻璃珠堆积模型的实验分析数据与RGPZ模型的预测结果进行验证。所用的玻璃珠是高磨圆度的碳酸钠和碳酸钙玻璃小球,它们随机堆积在直径2.54 cm,长2.5和5 cm的柱形单元中,样本饱和0.1 mol NaCl溶液,且已知NaCl溶液的密度和电阻率,用医用P-500活塞泵缓慢排替水溶液。渗透率适用于5个流速(每分钟的体积流量)即0.1、0.5、1.0、4.0和8.0 cm3/min对应于21.59 cm直径的生产孔,它们是用Keithley 2700数字测量仪和数据采集系统及高分辨率压差传感器记录不同的压强换算得到[9]。孔隙度用重量法测量得到,针对每个流速计算一个渗透率,在该流速范围内,发现渗透率没有系统变化。接着用计算的渗透率的算术平均及它们的最大及最小范围作为误差棒。样本的复电阻率由Solartron 1260阻抗分析仪以及工作频率0.1 Hz～1 MHz的涂铂-铂标准电极测量得到[9]。为避免流动电位造成的系统误差,测量值在没有流体流动时进行。胶结指数是由孔隙度和1 kHz的电阻率模值计算得到,玻璃珠堆积体测得的渗透率见参考文献[9]。

图2(a)给出了预测的和测量的渗透率的对比,用本文的新模型和其他作者的数据预测渗透率。输入的数据有玻璃珠堆积、非固结和固结砂岩[21],及熔结的玻璃珠[22]。可以看到,所有实验数据均显示RGPZ方程预测的渗透率在6个量级的变化范围上是极好的。图2(b)显示了测得的渗透率随颗粒直径的变化关系,且比较了RGPZ模型和其他模型的结果。很明显,RGPZ和Berg模型与修正的Kozeny-Carman模型或Van Baaren模型相比,其预测结果相对要好,RGPZ模型是这里测试的4个模型中最为稳健的。

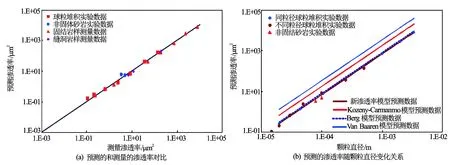
图2 玻璃球堆和其他数据的测量渗透率和预测渗透率比较

2.2 实际岩石样本数据的渗透率预测

用代表不同岩性范围的65个岩样的测量渗透率值[9]与RGPZ及其他模型预测的渗透率值比较。每种情况下,渗透率均用氦气测量,且进行了Klinkenberg和Forscheimer效应校正。孔隙度用氦比重测得而MICP利用压汞孔隙度测量仪测得。地层因素和胶结指数用工作频率为1 kHz阻抗谱分析仪测得,岩石用高浓度的NaCl盐水饱和。所用的砂岩有代表各向同性纯砂岩的Berea砂岩和固结很好的颗粒状长石石英砂岩[23]。该岩类有中等孔隙度(12%～24%)及中高渗透率(0.49～1.97 μm2)的样本。还有以非胶结和胶结2种状态出现的各向同性Lochaline纯砂岩,其非胶结形式以分选好的次圆形颗粒形式出现(50～100 μm),有中高孔隙度(18%～25%),及中高渗透率(0.49～1.97 μm2)。而胶结好的Lochaline砂岩与非胶结砂岩岩石成分相同,但经历了在原生蚀变颗粒上发生的硅次生沉淀作用,形成了代表极细孔喉层状颗粒的边界。胶结好的砂岩渗透率和孔隙度非常低[φ为2%～8%;K为(0.986 9～4.93)×10-4μm2][20]。

为考察RGPZ模型对各向异性地层的适应性,用Fascally砂岩或粉砂岩样本的实验数据进行实验验证。该砂岩中有大量的黏土矿物,取的岩心有的平行于层面,也有的垂直于层面,还有的与层面成45 °,用于考查层面对模型预测样品渗透率能力的影响,还对多个Portland和Purbeck灰岩样本进行了测试。图3显示了文献[23]给出的岩性样本用RGPZ和Kozeny-Carman模型预测渗透率的结果。从图3可见,对于大部分岩石类型,RGPZ模型可以给出更好的预测结果,特别是在高渗透率时,预测的数据紧紧聚焦到一条线的附近。图3(a)表明,RGPZ模型预测渗透率的能力在低孔隙度时有所降低,但仍然落在合理的范围内。应当注意到,对各向异性的Fascally砂岩垂直层面的渗透率估计值整体有5倍的偏高。

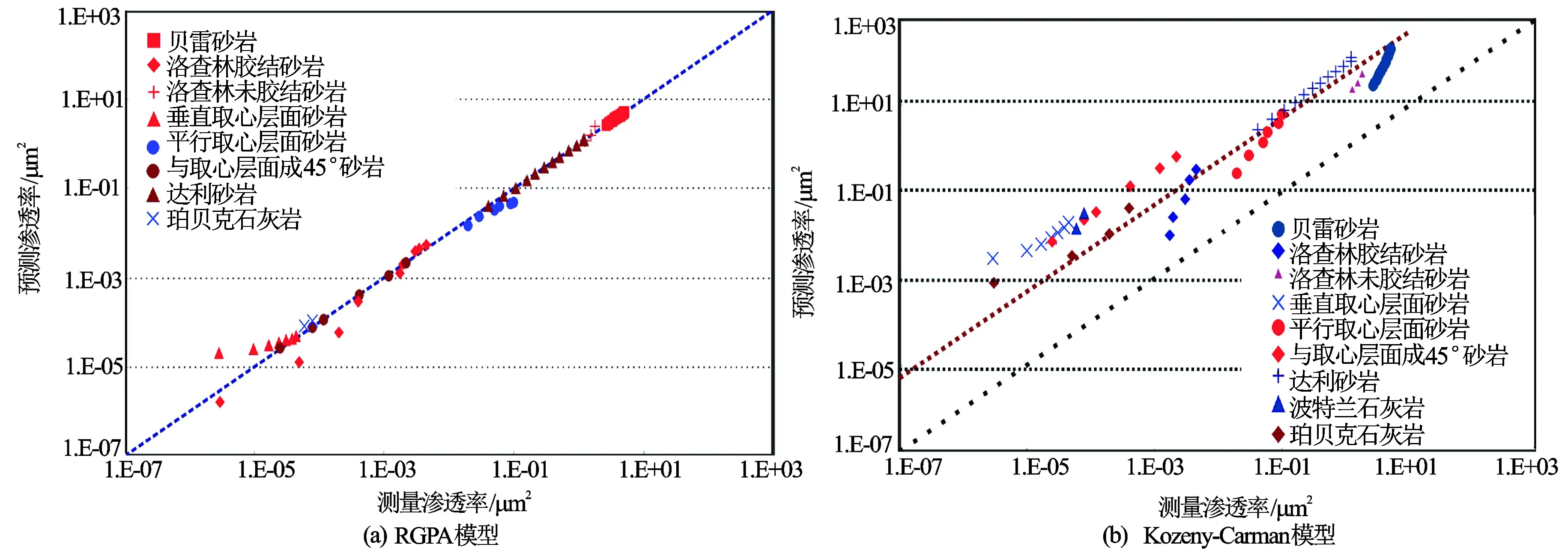
图3 文献[23]中65个砂岩的碳酸岩样品测量和预测渗透率的对比

相比较而言,Kozeny-Carman模型给出的预测结果更分散,显示了高渗透率时正确的预测趋势(即与d2成比例),但在所有样本上预测的渗透率要高2个数量级左右。Kozeny-Carman模型提供的预测结果比实验测量值偏高的趋势在低渗透率端增大。Kozeny-Carman模型得到了正确的渗透率变化趋势,但计算得到的结果不精确,均高估了1～2个数量级。Kozeny-Carman模型在预测垂直层面的取心样品的渗透率时表现出最大的困难,预测结果偏高3个量级。

尽管上文已经显示了RGPZ模型对理想球体的实验数据、岩石的实验分析数据以及测井数据得到了较好的渗透率预测结果,但该模型的应用有局限:①尽管RGPZ模型是由岩电参数分析导出,并不是实验数据建立的经验关系,但公式中涉及的颗粒大小参数,目前仍难以用测井数据准确求取,限制了模型的应用范围和精度;②若将RGPZ模型应用于核磁共振测井数据,那么公式中的颗粒大小目前只能将之与T2弛豫时间相关联,用经验关系求取;③RGPZ模型中用到的F和m值必须由饱和盐水的岩石测量得到,对于含油气岩样需要使表面导电性影响降至最小;④当φ→1(即100%孔隙度时),RGPZ方程不适用,这是该方程对极限边界条件的不适用;⑤在RGPZ方程应用于非球形颗粒时,需要假设所计算的颗粒粒径远大于最大颗粒粒径与最小颗粒粒径的差,这对于大多数沉积岩地层是正确的。

3 RGPZ渗透率估算模型在低孔隙度低渗透率储层评价中的应用

由于渗透率的影响因素太多,特别是低孔隙度低渗透率储层,目前还大多应用统计方法根据特定地区的样品化验分析渗透率建立经验关系。下边给出的应用实例是鄂尔多斯盆地南部某探区的三叠统延长组中低孔隙度低渗透率和特低渗透率储层的实际测井资料的计算结果。由于研究区三叠统延长组储层岩性较为复杂,石英、长石、岩屑和胶结物的含量对声波、中子和密度孔隙度测井响应的影响较大,尤其储层中的白云质与灰质胶结物含量多少对孔隙度计算中的骨架参数选择有严重影响,为消除孔隙度的不确定性对评价RGPZ渗透率估算模型性能的影响,均选用了岩性和胶结物特性相类似井的测井资料进行分析和对比。

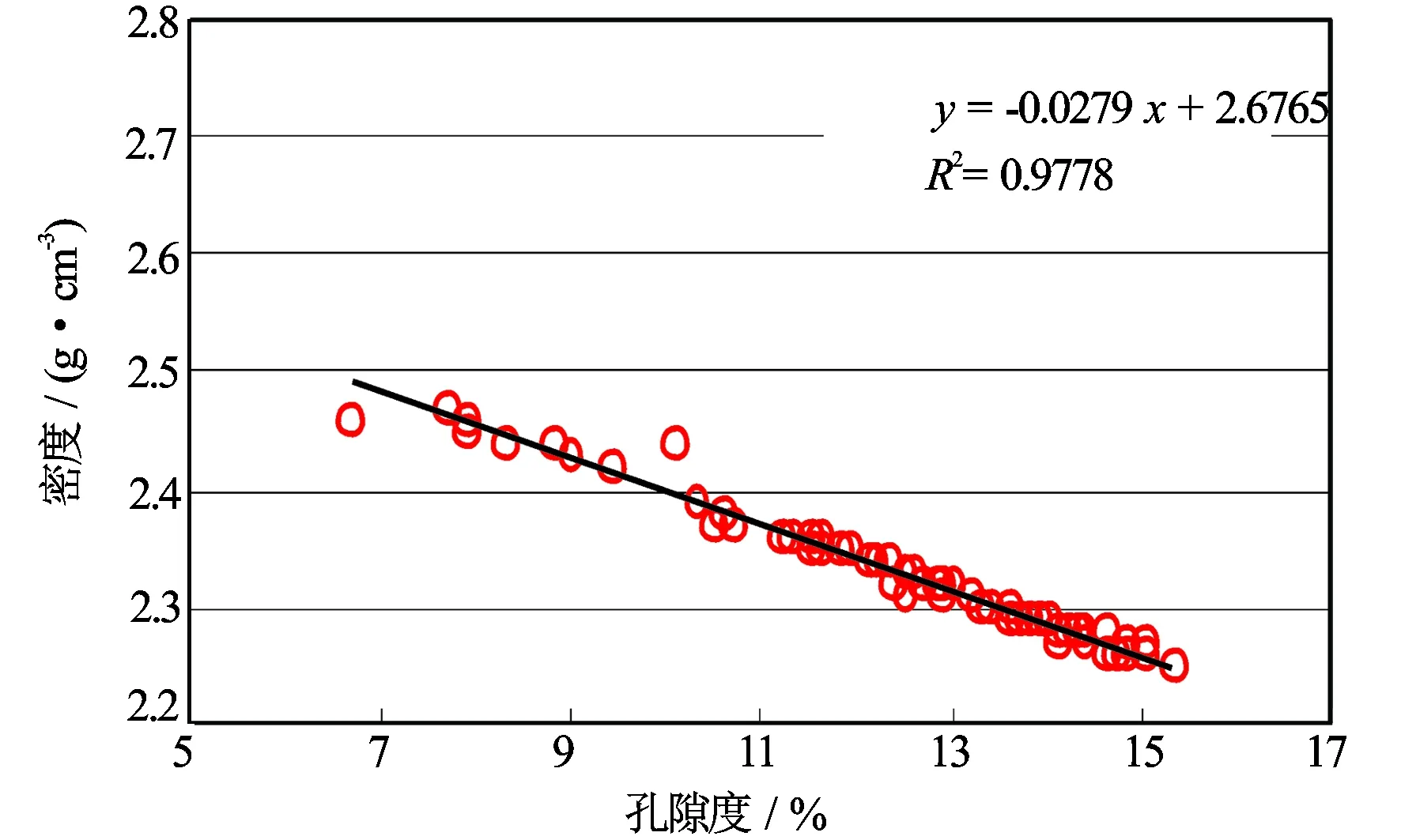
图4 某井区3口取心井78块岩样分析岩心分析孔隙度与密度关系

图4给出了某井区3口取心井78块岩样分析孔隙度与密度关系。由图4可见,由于研究区范围较小,井间距不大,岩性变化对密度与孔隙度的关系影响不大,利用密度测井经过井眼影响校正后得到的孔隙度较为可靠。在计算渗透率中,均采用由密度测井和式(9)估算孔隙度。

DEN=-0.0279φ+2.6765R2=0.9778

(9)

图5给出了研究区现有的B和C这2口取心井的岩电分析数据最小二乘拟合得到的储层孔隙胶结指数,拟合关系如式(10)所示。渗透率计算中均采用此固定的胶结指数。

F=1.5733φ-1.6073R2=0.9229

(10)

RGPZ渗透率估算模型中另一个重要的参数粒度直径d 的计算也是测井评价的一个难题。该区采用自然伽马的泥质含量Vsh、声波时差AC 和深电阻率Rt这3 个测井响应计算相对参数，再与化验分析粒径的拟合关系进行预测。式中,Vsh是泥质体积分数;GRmax、GRmin和GR分别是泥岩层、纯砂岩层和泥质砂岩层自然伽马值;φAC是声波时差计算的视孔隙度;Δtma、Δtf和Δt分别是纯砂岩地层骨架、孔隙流体和孔隙性砂岩层的声波时差值;IRt是电阻率计算的地层含泥质指数,Rt,max、Rt,sh和Rt分别是纯砂岩地层、泥岩层和泥质砂岩层的电阻率值。相应地,砂岩层的粒径拟合关系为

d=Aexp(-DVsh)+BIAC+CIRt

(11)

式中,A、B和C为3个权系数,D为拟合系数。

图6给出了研究区A井延长组长3段分析孔隙度/渗透率与测井计算的孔隙度/渗透率的对比关系。由图6可见,总体上,孔隙度与渗透率计算与岩心分析数据吻合较好,但在含泥质较重的层段,由于泥质中含量校正中存在误差,造成了计算孔隙度偏高,相应地计算的颗粒直径偏小,最终导致含泥质地层内,KRGPZ计算的渗透率偏高,而其他层段计算渗透率与岩心分析渗透率吻合较好。

图7给出了研究区B井延长组长3段分析孔隙度/渗透率与测井计算的孔隙度/渗透率的对比关系。由图7可见,该井孔隙度与渗透率计算结果与岩心分析数据比图6的A井吻合更好,但在含泥质较重的层段,也存在计算孔隙度偏高的现象。

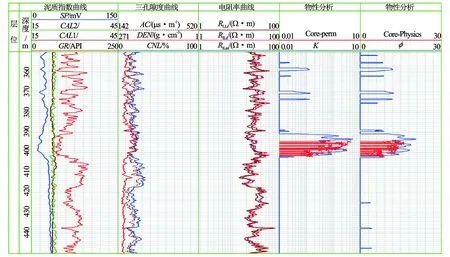
图6 研究区A井延长组长3段分析孔隙度/渗透率与测井计算的孔隙度/渗透率的对比关系

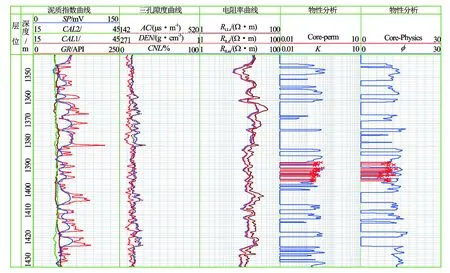
图7 研究区B井延长组长3段分析孔隙度/渗透率与测井计算的孔隙度/渗透率的对比关系

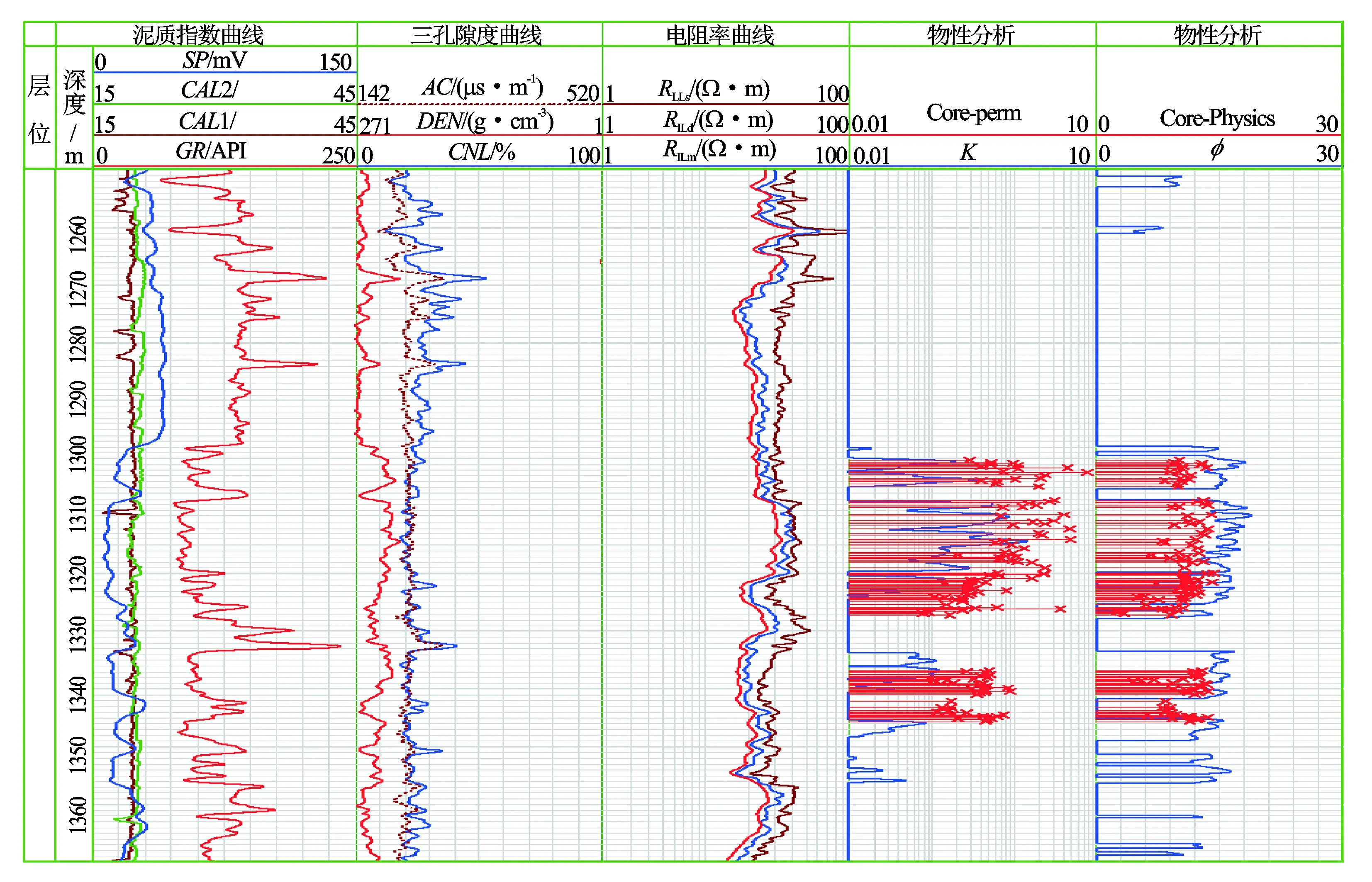
图8 研究区C井延长组长8段分析孔隙度/渗透率与测井计算的孔隙度/渗透率的对比关系

图8给出了研究区C井延长组长8段分析孔隙度/渗透率与测井计算的孔隙度/渗透率的对比关系。由图8可见,与延长组长3段相比,该井长8段计算的孔隙度明显比岩心分析孔隙度高,实际上,该层段普遍发育微裂缝,取心收获层段和岩心分析孔隙度对微裂缝不敏感,而且岩电分析数据中,长8段的岩心数据占比较少,由岩心分析数据得到的胶结指数基本没有反映微裂缝的影响。因此,该层段上用KRGPZ模型计算的渗透率普遍小于岩心分析渗透率。

4 结 论

(1) 在分析经典渗透率计算关系的适用条件的基础上,考虑孔隙介质流体流动特性与电流导通关系的相关性,导出了估算孔隙介质渗透率的模型。该模型综合了孔隙度/颗粒直径和反映孔隙结构几何特征的岩电参数,从理论上可以更好地适应不同岩性和不同孔隙结构储层的渗透率计算。

(2) 用前人发表的实验测量数据及胶结和非胶结砂岩岩心分析数据,验证了RGPZ渗透率计算模型的有效性。应用鄂尔多斯盆地某井区中低孔隙度渗透率地层的岩电分析数据和测井数据估算的RGPZ渗透率与岩心分析渗透率的对比表明,泥质对颗粒直径计算结果的影响使计算的渗透率在泥质较重的层段偏高。

(3) 对于裂缝发育层段的渗透率计算需要利用新的手段得到各向异性的胶结指数和不同方向的粒径大小,进而计算不同方向的渗透率,这是进一步深入研究的方向。

参考文献:

[1] Berg R R. Method for Determining Permeability from Reservoir Rock Properties [C]∥Transactions of the Gulf Coast Association of Geological Societies, 1970: 303-317.

[2] Kostek S, Schwartz L M, Johnson D L. Fluid Permeability in Porous Media, Comparison of Electrical Estimates with Hydrodynamical Calculations [J]. Physics Review: B, 1992, 45(1): 186-195.

[3] Coates G R, Dumanoir J L. A New Approach to Improved Log Derived Permeability [J]. The Log Analyst, 1974, 15: 17-23.

[4] Coates G R, Peveraro R C A, Hardwick A, et al. The Magnetic Resonance Imaging Log Characterized by Comparison with Petrophysical Properties and Laboratory Core Data [C]∥Proceedings of the 66th Annual Technical Conference and Exhibition, SPE 22723, 1991: 627-635.

[5] Carman P C. Flow of Gases Through Porous Media [M]. Amsterdam: Elsevier Science Publishing Company, Inc., 1956: 197-212.

[6] Helle H B, Bhatt A, Ursin B. Porosity and Permeability Prediction from Wireline Logs Using Artificial Neural Networks: A North Sea Case Study [J]. Geophysical Prospecting, 2001, 49(4): 431-444.

[7] Carman P C. The Determination of the Specific Surfaces of Powders I [J]. Journal of the Society of the Chemical Industrialists, 1938, 57: 225-234.

[8] Van Baaren J P. Quick-look Permeability Estimates Using Sidewall Samples and Porosity Logs [C]∥Transactions of the 6th Annual European Logging Symposium, Society of Petrophysicists and Well Log Analysts, 1979: 19-25.

[9] Glover P W J, Zadjali I I, Frew K A. Permeability Prediction from MICP and NMR Data Using an Electrokinetic Approach [J]. Geophysics, 2006, 71(4): 49-60.

[10] Nelson P H. Permeability-porosity Relationships in Sedimentary Rocks [J]. The Log Analyst, 1994, 35(3): 38-62. [11] Hidajat I, Mohanty K K, Flaum M, et al. Study of Vuggy Carbonates Using NMR and X-Ray CT Scanning [J]. Society of Petroleum Engineers Reservoir Evaluation and Engineering, 2004, 7(5): 365-377.

[12] Hidajat I, Singh M, Cooper J, et al. Permeability of Porous Media from Simulated NMR Response [J]. Transport in Porous Media, 2002, 48(2): 225-247.

[13] Swanson B F. A Simple Correlation Between Permeabilities and Mercury Capillary Pressures [J]. Journal of Petroleum Technology, 1981, 33(12): 2498-2504.

[14] Berg R R. Capillary Pressures in Stratigraphic Traps [J]. AAPG Bulletin, 1975, 59(6): 929-956.

[15] Bussian A E. Electrical Conductance in a Porous Medium [J]. Geophysics, 1983, 48(9): 1258-1268.

[16] O’Konski C T. Electric Properties of Macromolecules V: Theory of Ionic Polarization in Polyelectrolytes [J]. Journal of Chemical Physics, 1960, 64(5): 605-619.

[17] Johnson D L, Sen P N. Dependence of the Conductivity of a Porous Medium on Electrolyte Conductivity: Physics Review: B, 1988, 37(7): 3502-3510.

[18] Schwartz L M, Sen P N, Johnson D L. Influence of Rough Surfaces on Electrolytic Conduction in Porous Media [J]. Physics Review: B, 1989, 40(4): 2450-2458.

[19] Sen P N, Scala C, Cohen M H. A Self-similar Model for Sedimentary Rocks with Application to the Dielectric Constant of Fused Glass Beads [J]. Geophysics, 1981, 46(5): 781-795.

[20] Bernabé Y, Revil A. Pore-scale Heterogeneity, Energy Dissipation and the Transport Properties of Rocks [C]∥Geophysical Research Letters, 1995, 22(12): 1529-1532.

[21] Chauveteau G, Zaitoun A. Basic Rheological Behavior of Xanthan Polysaccharide Solutions in Porous Media [M]. Amsterdam: Elsevier Science Publishing Company, Inc., 1981: 197-212.

[22] Johnson D L, Plona T J, Kojima H. Probing Porous Media with 1st Sound, 2nd Sound, 4th Sound and 3rd Sound [C]∥American Institute of Physics Conference Proceedings, 1987, 154: 243-277.

[23] Glover P W J, Gomez J B, Meredith P G, et al. Damage of Saturated Rocks Undergoing Triaxial Deformation Using Complex Electrical Conductivity Measurements: Experimental Results [J]. Physics and Chemistry of the Earth, 1997, 22(1): 57-61.