利用小波尺度谱同步平均的时频脊故障特征提取

李宏坤, 徐福健, 高巧红, 汪寅虎

(1.大连理工大学机械工程学院， 辽宁 大连 116024； 2.大连博瑞重工有限公司, 辽宁 大连 116050)

利用小波尺度谱同步平均的时频脊故障特征提取

李宏坤1, 徐福健1, 高巧红2, 汪寅虎1

(1.大连理工大学机械工程学院， 辽宁 大连 116024； 2.大连博瑞重工有限公司, 辽宁 大连 116050)

旋转机械的早期故障特征微弱，容易受到噪声的干扰，不容易准确识别。小波尺度谱存在受噪声干扰影响大、高频部分频率分辨率低等缺点, 对小波尺度谱进行重排可以提高其时频聚集性。为此，结合小波尺度谱同步平均和小波脊线分析的优点，提出了基于时频脊线特征提取方法。首先对多周期的振动信号进行小波连续变换，并重排小波尺度谱；再根据信号的周期性，对尺度谱进行同步平均；最后提取同步平均后的尺度谱小波脊线，计算信号的包络幅值并进行频谱分析，最终提取出弱故障特征。通过仿真和实例验证了本方法的有效性，为旋转机械的早期故障诊断提供了新方法。

故障诊断； 旋转机械； 小波尺度谱； 时频脊； 微弱故障

引 言

振动信号分析广泛的应用于旋转机械的故障诊断中。其可分为3个步骤，首先是故障信号的获取；其次是故障特征的提取；最后是模式识别和故障诊断。其中故障特征提取是进行旋转机械故障诊断的核心问题[1]。早期故障信号的特征微弱，容易被噪声掩盖。因此故障的识别对于设备故障的早期预警意义重大，如何从强噪声干扰中识别弱故障信息，实现故障的早期预警得到了广大学者的广泛关注[2-3]。在实际工程中，旋转机械振动信号由于受到各种干扰噪声的影响，往往表现为调制形式，解调分析是一种常用的提取旋转机械故障特征的信号处理方法[4]。

小波脊线是时频面上不同时刻信号小波系数的模取极大值点的集合，这些点称为小波脊点。通过分析小波脊线可以得到信号的瞬时频率(IF)和瞬时幅值(IA)信息。秦毅等[5]指出Hilbert变换解调、检波滤波解调等解调方法存在的局限性，而小波脊线的解调方法能有效地提取旋转机械故障振动信号的特征，并结合实例验证了小波脊线解调的优越性。何清波等[6-7]提出了基于时间尺度流形的小波脊线的解调方法，实现对轴承和齿轮故障的自动诊断。为小波脊线在弱故障特征提取提供一条新的方法。

旋转机械的周期性决定了其振动信号具有广义的周期性，时域同步平均技术可以从受噪声干扰的信号中提取周期性波形，当故障特征微弱时，结合重排尺度谱和时域同步平均技术能够较好的降低噪声干扰[8]。本文结合小波尺度谱进行同步平均和小波脊线的解调方法，对弱故障信息特征进行了准确地提取。结果表明该方法可以有效地从噪声干扰中识别微弱故障特征，实现了旋转机械早期的故障特征提取。

1 小波脊理论及IA计算[6,7]

1.1 小波脊线

(1)

(2)

(3)

其中

(4)

(5)

由驻点定义，在小波脊线上有

(6)

(7)

1.2IA计算

Morlet小波在时频域都具有很好紧支性和局部化特性，复Morlet小波定义如下

(8)

式中fb为带宽参数，fc为小波中心频率。若采样频率为fs，则频率和尺度的关系为

(9)

将Morlet小波作为母小波进行小波变换，可得小波脊点对应的小波系数表示为

(10)

(11)

(12)

(13)

则有

(14)

小波脊线提取后，信号x(t)的IA(包络幅值)和IF可由下式计算：

(15)

(16)

因此通过上面的推导可以看出，小波脊线可以计算瞬时频率与瞬时幅值，实现对信号的解调分析。同时可以根据脊线上的小波系数对信号重构，因此获取小波脊线具有较好的实际工程应用价值。

1.3 小波脊提取

(17)

需要指出的是为了更精确地提取小波脊线，需要选择一个较窄的尺度区间，然后对此尺度区间内的小波尺度谱系数进行小波脊提取，何清波等[6-7]提出了一个3 dB带宽的尺度区间选择方法。在小波系数幅值较高的区域进行小波脊提取符合脊线的特点，并且减少计算时间，提高效率。另外，此算法每次提取一条脊线，对于多分量信号，同一时刻会有多个局部极大值点，即存在多条脊线，此种情况可对应各个分量选择各自不同尺度区间分别求取其小波脊线。

2 小波尺度谱同步平均方法

2.1 小波尺度谱重排

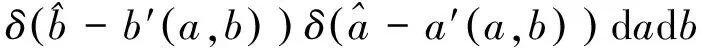
(18)

(19)

(20)

(21)

更多关于小波尺度谱重排的详细信息可参考文献[14]。小波尺度谱重排在一定程度上克服了时频分布聚集性矛盾，减少了干扰项，提高了信号时频分布的可读性。

2.2 小波尺度谱同步平均

在实际工程应用中，旋转机械运行时的振动信号随机器的周期运转具有周期性，其周期与设备的运转周期具有倍数关系。这样的信号非平稳特性具有周期性，称为循环平稳信号。在实际设备的循环平稳信号中往往夹杂着噪声干扰，若噪声干扰较强时，影响对周期性确定信号的识别，尤其是对弱周期信号识别。同步平均技术可以削弱观测信号中的随机成分，具有滤波降噪的特性，提取与平均周期相关的确定性信号[15]。

(22)

式中T为周期，P为周期个数，l为整数。

(23)

总结上述方法，首先对具有循环平稳性质的旋转机械振动信号进行Morlet小波的连续小波变换，获得小波多尺度谱并进行重排以提高时频聚集性，然后对重排小波多尺度谱的系数矩阵进行同步平均，以降低噪声干扰，获得平均后的小波尺度谱，使用成本函数脊线提取方法提取小波脊线，由不同脊点对应的尺度谱系数和式(15)计算振动信号的IA波形，对IA曲线进行FFT，依据特征频率识别故障类型。

3 仿真分析

为验证基于小波尺度谱小波脊线解调分析方法的有效性，对仿真信号进行分析。选取一个谐波频率调制的指数衰减的脉冲来仿真模拟机械冲击信号，在对文献[16]进行研究的基础上，对信号进行改进的模型的表达式为

(24)

图1 仿真信号时域波形Fig.1 Time-domain waveforms of the simulation signals

图2 仿真信号频谱Fig.2 Spectrum of the simulation signal

对单周期信号进行连续小波变换和尺度谱重排，结果表明单周期谱图分布比较杂乱，没有仿真信号模拟的冲击特征，无法在较强的噪声干扰条件下实现弱冲击特征的识别，而多周期同步平均小波尺度谱结果较好[8]。50个周期平均后的小波重排尺度谱如图3所示。可以发现在谱图上在8 000 Hz处存在冲击特征，这与仿真信号中的频率成分相对应。为了识别冲击频率，使用小波脊线解调方法对其进行进一步分析。

根据频率分布的特点，同时结合小波脊线的计算公式，选择尺度区间为[2.393,4.339]，提取小波尺度谱的小波脊线，由式(10)将尺度转化成频率，结果如图4所示;再由式(15)计算IA如图5(a)所示，并对IA进行FFT变换，其频谱如图5(b)所示。IA波形和图1(a)中冲击相吻合，频谱分析得出了冲击频率125 Hz及其倍频，验证了方法有效性。

图3 50周期同步平均尺度谱Fig.3 The scalogram under synchronous averaged

图4 尺度谱同步平均后小波脊线Fig.4 Wavelet ridge of the scalorgram under synchronous averaged

图5 仿真信号的IA波形及其频谱Fig.5 Time-domain waveforms and spectrum of simulation signal′s instantaneous amplitude

4 实例分析

为了进一步验证本文所述方法的有效性，采用滚动轴承故障信号进行分析，该信号来自美国宇航局(NASA)网站[17]，由辛辛那提大学智能维护中心提供。轴承试验台的转轴上安装4个轴承，交流电动机通过带传动带动转轴转动，转速约为2 000 r/min。通过弹簧机构在转轴径向施加6 000 b(2 724kg)的力，每个轴承强制润滑。轴承为Rexnord公司的ZA-2115双列滚子轴承。该轴承每列有16个滚动体，节圆直径为71.5 mm，滚子直径为8.4 mm，接触角为15.17°。应用NI DAQCard-6062E数据采集卡、PCB 353B33加速度传感器和LabVIEW开发的数据采集软件采集轴承座处的振动信号，采样频率为20 kHz，采样长度为20 480点，每隔10 min采集一次，直至发现滚动轴承1外环出现严重磨损。如图6为轴承试验台示意图。

图6 轴承试验台示意图Fig.6 Bearing test rig

选择试验后期轴承外环磨损较严重的一组数据，图7为其时域波形和频谱。从图7的时域波形中可发现明显的冲击特征。根据时域波形出现的连续冲击时间间隔得到轴承的实际转速为1 948 r/min，轴承的外环故障频率为230 Hz。因为严重磨损传统方法就能识别，而早期故障不易识别。图8为早期故障。轴承出现了明显的外环磨损时只需要进行频谱分析即可对其进行诊断，但是实际生产中，做到这一点显然不够，在设备故障初期就要做出精确的诊断。

图7 轴承严重磨损时的波形和频谱Fig.7 Time-domain waveform and spectrum of outer ring with severe wear

图8 轴承轻微磨损时的波形和频谱Fig.8 Time-domain waveform and spectrum of outer ring with slight wear

选择试验中轴承外环轻微磨损的一组数据，该信号的时域波形如图8(a)所示，在时域波形上并无明显的连续冲击特征；图8(b)所示频谱中特征频率不明显，并不能作为轴承外环故障诊断依据，这也说明常规的频谱分析无法检测出轴承的微弱故障信息。考虑到同步周期存在一定的误差，那么分别取区间[604,614]内的整数作为同步平均的点数，分析结果发现当同步平均的点数为608时的效果最好，即选用30.4 ms作为同步周期。对轴承外环早期磨损时的振动信号进行分析，对30个同步周期的振动信号进行连续小波变换，获得小波尺度谱，并进行重排处理，结果如图9所示。在频率4 500 Hz附近频段，具有明显规律的连续冲击特征。文献[7]已经论述了如果不对尺度谱进行重排处理，直接获得同步平均后的尺度谱，相对重排尺度谱的时频聚集性较差，这里不再做详细对比。

图9 多尺度同步平均的小波重排尺度谱Fig.9 The scalogram of the signals under synchronous average

图10 轴承信号的小波脊线Fig.10 Wavelet ridges of bearing signals

选择尺度区间为[4.064,6.244]，在此区间，对重排尺度谱同步平均后进行小波脊提取，由式(9)将尺度转化成频率，结果如图10所示。进行IA计算和频谱分析，结果如图11所示。图11(a)非常清晰地显示了轴承轻微外环故障信号中的冲击成分周期特性。图11(b)所示的谱线中，频率230.3 Hz及其倍频显示了轴承发生了外环故障。也就是通过时频同步平均分析，增强信号中的微弱冲击成分，同时采用小波脊线重构方法，可以准确获取信号中包含的冲击成分，通过对IA信息的计算，可以清楚获取包含冲击信号的频域信息，能够很容易得到滚动轴承的故障特征频率，实现轴承故障的早期识别。

图11 轴承信号IA波形及其频谱Fig.11 Time-domain waveforms and spectrum of instantaneous amplitude

图12 信号共振解调分析Fig.12 Signal resonance demodulated analysis result

同时对此信号采用共振解调分析，先对信号进行滤波，滤波后的包络波形及其对应的频谱如图12所示。获取的特征频率为224.6 Hz，其与实际故障频率230.3 Hz有一定的差异。同时没有清晰的倍频关系，在共振解调分析中表明不同的滤波频带和中心频率得到的结果有很大的差异，影响结果分析的准确性。因此可以说明采用本文方法具有较好的准确性。

5 结 论

旋转机械早期故障的识别是机械故障诊断中的难点之一，本文基于旋转机械振动信号具有广义周期性的特点，采用小波尺度谱同步平均的方法有效的提高了信噪比，通过最小化成本函数求取小波尺度谱系数模的局部极大值方法提取小波脊线。并采用频谱分析能够清楚地获取调制中的冲击信号，通过仿真分析与实例分析验证了该方法提取设备弱信息的能力，为旋转机械早期故障诊断提供了新的方法。

致谢:研究过程中得到中国科学技术大学何清波副教授对小波脊提取方法的大力帮助，在此表示感谢。

[1] 杨叔子，史铁林，丁洪. 机械设备诊断的理论、技术与方法[J]. 机械工程学报，1992，5(3)：193—200.

Yang Shuzi，Shi Tielin，Ding Hong. The theory, technique and method for mechanical device diagnosis[J]. Chinese Journal of Mechanical Engineering, 1992，5(3)：193—200.

[2] 蒋永华. 旋转机械非平稳信号微弱特征提取方法研究[D]. 重庆：重庆大学，2010.

Jiang Yonghua. Research on weak feature extraction of nonstationary signals of rotating machinery[D]. Chongqing：Chongqing University，2010.

[3] 李舜酩，许庆余. 微弱振动信号的谐波小波频域提取[J].西安交通大学学报，2004，38(1)：51—55.

Li Shunming，Xu Qingyu. Harmonic wavelet extraction for weak vibration signal in frequency domain[J]. Journal of Xian Jiao Tong University，2004，38(1)：51—55.

[4] Fan X F，Zuo M J. Gearbox fault detection using Hilbert and wavelet packet transform [J]. Mechanical Systems and Signal Processing，2006，20(4)：966—982.

[5] 秦毅, 秦树人, 毛永芳. 基于小波脊线的解调方法及其在旋转机械故障诊断中的应用[J] . 机械工程学报, 2009, 45(2) ：231—237.

Qin Yi，Qin Shuren，Mao Yongfang. Demodulation approach based on wavelet ridge and its application in fault diagnosis of rotating machinery [J]. Chinese Journal of Mechanical Engineering，2009，45(2)：231—237.

[6] Wang J，He Q B，Kong F R. Automatic fault diagnosis of rotating machines by time-scale manifold ridge analysis[J]. Mechanical Systems and Signal Processing，2013，40(1):237—256.

[7] He Q，Wang X. Time-frequency manifold correlation matching for periodic fault identification in rotating machines[J]. Journal of Sound and Vibration，2013，332(10):2 611—2 626.

[8] 李宏坤，练晓婷，周帅. 小波尺度谱同步平均在弱信息识别中的应用[J]. 机械工程学报, 2013，49(5):66—72.

Li Hongkun , Lian Xiaoting, Zhou Shuai. Application investigation on weak information classification by using wavelet scalogram synchronous averaging[J]. Chinese Journal of Mechanical Engineering，2013，49(5):66—72.

[9] Mallat S. A Wavelet Tour of Signal Processing[M]. 2nd ed. Beijing： China Machine Press, 2003.

[10]Liu H, Cartwright A N, Basaran C. Moiré interferogram phase extraction: a ridge detection algorithm for continuous wavelet transforms [J]. Applied Optics，2004，43(4):850—857.

[11]Delprat N, Escudii B, Guillemain P，et al. Asymptotic wavelet and Gabor analysis: Extraction of instantaneous frequencies[J]. Information Theory，IEEE Transactions on， 1992，38(2):644—664.

[12]朱洪俊，王忠，秦树人. 小波变换对瞬态信号特征信息的精确提取[J]. 机械工程学报，2005，41(12) ：196—199.

Zhu Hongjun, Wang Zhong, Qin Shuren. Accurate extraction for the characteristic information of transient signal with wavelet transforms[J]. Chinese Journal of Mechanical Engineering，2005，41(12)：196—199.

[13]彭志科，何永勇，褚福磊. 小波尺度谱在振动信号分析中的应用研究[J]. 机械工程学报，2002，38(3)：122—126.

Peng Zhike，He Yongyong，Chu Fulei. Using wavelet scalogram for vibration signals analysis[J]. Chinese Journal of Mechanical Engineering，2002，38(3)：122—126.

[14]彭志科. 小波分析在旋转设备故障诊断中的应用[D]. 北京：清华大学，2002.

Peng Zhike. Application of wavelet analysis in fault diagnosis of rotating machinery[D]. Beijing：Tsinghua University，2002.

[15]罗德扬. 时域同步平均原理与应用[J]. 振动、测试与诊断，1999，19(3)：202—207.

Luo Deyang. Time-domain synchronous average principle and application[J]. Journal of Vibration，Measurement and Diagnosis，1999，19(3)：202—207.

[16]Sheen Y T. A complex filter for vibration signal demodulation in bearing defect diagnosis[J]. Journal of Sound and Vibration，2004，276(1): 105—119.

[17]Lee J, Qiu H, Lin J． Rexnord Technical Services. ‘Bearing Data Set’, IMS, University of Cincinnati. NASA Ames Prognostics Data Repository, [http://ti.arc.nasa.gov/project/prognostic-data-repository]. NASA Ames, Moffett Field，CA，USA.

Fault feature extraction for synchronous averaging wavelet scalogram based on time-frequency ridge

LIHong-kun1,XUFu-jian1,GAOQiao-hong2,WANGYin-hu1

(1.School of Mechanical Engineering, Dalian University of Technology, Dalian 116024, China；2.DALIAN Borui Heavy Industry Company, Dalian 116050, China)

Early fault feature of rotating machinery is weak and interfered by noises, so it is difficult for accurate early fault detection. Wavelet scalogram is sensitively affected by the noise and it has low resolution for its high frequency components. Reassigned wavelet scalogram is applied to improve time-frequency concentration of the scalogram. Therefore, a weak fault feature extraction method is put forward based on time-frequency ridge by taking the advantage of the synchronous averaging and wavelet ridge. Firstly, multi-cycle signal is processed by continuous wavelet transformation and wavelet scalogram is reassigned. Then, the scalogram is synchronous averaged. After the wavelet ridge of scalogram is extracted, instantaneous amplitude curve of signal can be calculated, where the frequency spectrum analysis is used to extract fault characteristics. Both simulations and experiments investigation have been used to verify the effectiveness of this method. It can be concluded that this method will contribute to early fault diagnosis of rotating machinery.

fault diagnosis; rotating machinery; wavelet scalogram; time-frequency ridge; weak fault

2014-02-13；

2014-10-30

国家自然科学基金资助项目(51175057);中央高校基本科研业务费专项资金资助项目(DUT14ZD204)

TH165+．3； TN911.2

A

1004-4523(2015)03-0487-08

10.16385/j.cnki.issn.1004-4523.2015.03.020

李宏坤 (1974—)，男，教授,博士生导师。电话：(0411)84706561-8048;E-mail：lihk@dlut.edu.cn